Lista de exercicios prova P1

1
1ª Lista de Exercícios de Resistência dos Materiais e Estruturas - CIV 107 (Turma 21)
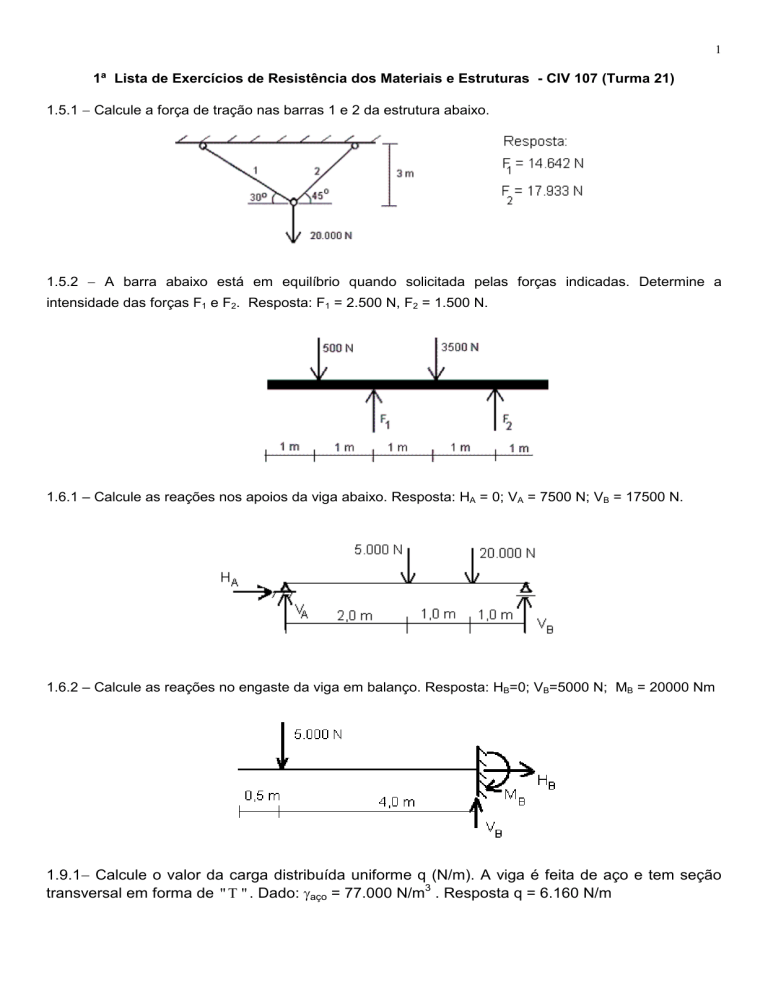
1.5.1 − Calcule a força de tração nas barras 1 e 2 da estrutura abaixo.
1.5.2 − A barra abaixo está em equilíbrio quando solicitada pelas forças indicadas. Determine a
intensidade das forças F1 e F2. Resposta: F1 = 2.500 N, F2 = 1.500 N.
1.6.1 – Calcule as reações nos apoios da viga abaixo. Resposta: HA = 0; VA = 7500 N; VB = 17500 N.
1.6.2 – Calcule as reações no engaste da viga em balanço. Resposta: HB=0; VB=5000 N; MB = 20000 Nm
1.9.1− Calcule o valor da carga distribuída uniforme q (N/m). A viga é feita de aço e tem seção
transversal em forma de " T " . Dado: γaço = 77.000 N/m3 . Resposta q = 6.160 N/m
2
2.1.1 − Coloque MPa em N/cm . Resposta: 1 MPa = 100 N/cm
2
2
2.1.2 − Calcule a tensão normal nas duas barras da treliça do problema 1.5.1. Dados: A1 = A2 = 10
−4
2
m.
Resposta: σ1 = 146,4 MPa; σ2 = 179,3 MPa.
2.1.3 − Duas barras de seção transversal circular são soldadas como mostra a figura abaixo. Calcule a
tensão normal nas duas barras. Resposta: σAB = 4,24 MPa; σBC = 1,53 MPa
2.1.4 – Uma barra prismática de comprimento longitudinal L = 5,0 m está pendurada verticalmente e
sujeita à ação de seu peso próprio. Calcule a maior tensão normal se for de:
a) Aço.
Dado: γ = 78480 N/m
b) Alumínio.
Dado: γ = 26487 N/m3
3
Resposta: a) σ = 0,39 MPa; b) σ = 0,13 MPa
2.2.1 – Uma barra prismática de seção transversal retangular (25 mm x 50 mm) e comprimento L = 3,6 m,
fica solicitada por uma força axial de tração F = 10 kN. O alongamento da barra (∆L) é de 1,2 mm. Calcule
a tensão de tração e a deformação linear específica. Resposta: σ = 8 MPa,
ε = 3,33 x 10 − 4
2.2.2 – Um elástico tem comprimento não esticado igual a 50 cm. Calcule a deformação linear específica
do elástico quando for esticado ao redor de um poste que tem diâmetro externo igual a 20 cm.
Resposta: ε = 0,257
2.3.1 – Uma barra prismática de seção transversal circular (d=55 mm) é comprimida por uma força axial F
= 196.200 N. Calcule a variação do diâmetro sabendo-se que a deformação linear específica longitudinal
εL é igual a − 9,62 x 10 − 4 e ν = 0,3. Resposta: ∆d = 0,0159 mm.
2.4.1 – A figura abaixo mostra o diagrama força – alongamento de um ensaio de tração simples de uma
barra de seção transversal circular (d = 15 mm). O comprimento inicial de referência da barra é igual a
350 mm. Calcule a tensão de escoamento e a tensão última.
3
2.5.1 – Calcule o módulo de elasticidade da barra do problema 2.2.1. Resposta: Ε = 24 GPa.
2.5.2 – Calcule o módulo de elasticidade da barra do problema 2.4.1. Resposta: Ε = 7,13 GPa
2.5.3 - Em uma barra prismática de 20 mm de diâmetro são feitas duas marcas distanciadas de 300 mm.
Determinar o módulo de elasticidade sabendo-se que solicitada por uma força axial de tração F = 10.000
N a distância entre as duas marcas é de 300,50 mm. Resposta: Ε = 19.098,6 MPa.
2.5.4 − Coloque GPa em N/cm2. Resposta: 1 GPa = 105 N/cm2
3.1.1 – Calcule o alongamento das duas barras do problema 1.5.1. Dados: A1 = A2 = 10 − 4 m2 ; Ε1 = Ε2 =
205 GPa. Resposta: ∆L1 = 4,29 mm; ∆L2 = 3,71 mm.
3.1.2 – Uma barra prismática colocada em um plano horizontal mede 7 metros. Calcule o alongamento da
barra quando for suspensa por uma extremidade. Dados: Ε = 205 GPa, γ = 77.000 N/m3. Resposta: ∆L =
9,20 x 10− mm
3
3.1.3 – A barra AB é rígida (indeformável) e de peso desprezível. Sabendo-se que P = 15.000 N, calcule:
a) a força de tração no cabo; b) o alongamento do cabo; c) a reação vertical na rótula A e d) o
deslocamento vertical do ponto de aplicação da força P (ponto B). Dados do cabo: Ε = 120 GPa; L = 3,0
m; área da seção transversal = 100 mm . Respostas: a) Fc = 20.000 N; b) ∆Lc = 5,0 mm; c) VA = 5.000
2
N(↓); d) ∆VB = 6,67 mm.
3.2.1 – Calcule os valores dos deslocamentos horizontais dos pontos 1 e 2. A barra tem seção transversal
circular com diâmetro φ = 13,82 mm. Dados: Ε = 120 GPa; F1 = 12.000N; F2 = 18.000 N.
Resposta: ∆1 = 3,0 mm; ∆2 = 4,0 mm
4
3.3.1 - A barra prismática abaixo é carregada axialmente pelas forças indicadas. Calcule as
reações HA e HB. Os engastes A e B são indeformáveis. Resposta: HA = 1000 N; HB = 2500 N
3.4.1 – A barra prismática abaixo está livre de tensão quando a temperatura é igual a 30 oC. Calcule a
o
tensão normal quando a temperatura descer para 26 C. Os engastes A e B são indeformáveis.
Dados: α = 30 x 10− / °C; Ε = 10,0 GPa. Resposta: σTração = 1,2 MPa.
6
4.4.1 – Uma liga de titânio tem módulo de elasticidade (ou módulo de Young) Ε = 120 GPa e coeficiente
de Poisson ν = 0,36. Calcule o módulo de elasticidade transversal da liga. Resposta: G = 44,12 GPa.
4.5.1 − Calcule a tensão cisalhante nos pinos da ligação abaixo e a tensão normal nas chapas. Dado: d =
12 mm. Resposta: τ = 22,10 MPa; σ = 25 MPa.
4.5.2 − Para a ligação abaixo, calcule:
a) o diâmetro “d” dos pinos sabendo-se que a tensão de cisalhamento é igual a 153 MPa;
b) a espessura “t” sabendo-se que a tensão normal é igual a 240 MPa.
Resposta: a) d = 9,12 mm; b) t = 1,25 mm