1. introdução - COLÉGIO ESTADUAL UNIDADE POLO ENSINO

PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Danilo Corci Batista
Tema: Uma Sequência Didática para o Movimento Retilíneo Uniforme
Assunto: Mecânica
1. INTRODUÇÃO
Não é difícil encontrarmos corpos que se movimentam com velocidade escalar
constante, como por exemplo: a propagação do som e da Luz para um determinado
meio sempre ocorre com velocidade escalar constante. A maioria dos professores de
Física da 1ª Série do Ensino Médio, não utilizam sequências didáticas para inserir de
forma investigativa os conteúdos a serem estudados. Esse trabalho propõe uma
sequência didática para o movimento retilíneo uniforme (MRU) de forma investigativa,
por meio de uma atividade experimental produzida com materiais de baixo custo. A
aplicação do experimento antes da introdução deste conteúdo possibilita aos alunos
o manuseio do material experimental, o levantamento e teste de hipóteses, e por fim
também proporciona caminhos para que eles tirem as suas devidas conclusões com
base nos resultados.
2. OBJETIVO
Verificar experimentalmente os conceitos básicos sobre velocidade constante e
suas relações com o movimento retilíneo uniforme.
3. MATERIAIS NECESSÁRIOS

Uma base retangular de madeira contendo um furo de diâmetro 3/8 ”, como
mostra a figura 1.
Figura 1: Bloco de Madeira com furo 3/8” no centro.

Uma barra rosqueada de 1m e diâmetro 3/8”, que se pode encontrar em
qualquer deposito de materiais de construção, como mostra a figura 2 abaixo.
Figura 2: Barra rosqueada 3/8”.

Uma arruela lisa de diâmetro 3/8”, que também, pode se encontrar em qualquer
deposito de materiais de construção, como mostra a figura 3 abaixo.
Figura 3: Arruela lisa 3/8”.
4. PROCEDIMENTOS
a) Marque na barra rosqueada intervalos de 10 cm.
Figura 3: Barra rosqueada com intervalos de 10 cm.
b) Encaixe a barra rosqueada no furo da base retangular de madeira (tal base de
madeira pode ser substituída por outra base qualquer desde que mantenha a
barra imóvel) e pronto já está montado o seu experimento, basta agora soltar a
arruela lisa na parte superior da barra rosqueada para observar que esta realiza
um MRU, como mostram as figuras 5 e 6 abaixo.
Figura 6: Abandono da arruela na parte superior da barra para
observação do MRU.
Figura 5: Encaixe da barra rosqueada na base
retangular de madeira montagem pronta do
experimento.
c) Realização do experimento: Com o auxílio de um cronômetro, solte a arruela
na parte superior da barra rosqueada e observando o momento em que esta
começa a realizar um movimento uniforme escolha uma marca na barra como
posição inicial e registre 5 vezes o tempo num percurso de 10 cm, mais 5 vezes
para um percurso de 20 cm e finalmente mais 5 vezes para um percurso de 30
cm. Em seguida faça a média aritmética dos tempos e registre-os na tabela
abaixo, esboçando em seguida o gráfico de espaço
X
tempo.
TABELA PARA REGISTRO DE DADOS
Espaço
(metros)
Tempo 1
(segundos)
Tempo 2
(segundos)
Tempo 3
(segundos)
Tempo 4
(segundos)
Tempo 5
(segundos)
Tempo
Médio
(segundos)
10 cm
20 cm
30 cm
FOLHA MILIMETRADA PARA ESBOÇO DO GRÁFICO
Velocidade
Média
(cm/s)
4.1 ATIVIDADES PROPOSTAS
1. Quais são as características do Movimento Retilíneo Uniforme e como
podemos classificar tal movimento?
2. Qual é o significado físico da inclinação da reta obtida no gráfico?
3. Qual é a relação existente entre uma equação de reta e a prática desenvolvida?
4. Durante a execução da prática coletamos algumas medidas e com as mesmas
encontramos velocidade média, verificando certamente que pequenas
diferenças entre tais velocidades foram encontradas. À que você atribui essas
diferenças? Existe alguma maneira de diminuí-las? Se sim, qual?
5. REFERÊNCIAS
BARRETO FILHO, B.; SILVA, C. X. Física aula por aula. São Paulo: FTD, 2010,
volume 1.
FUKE, L.F.; KAZUHITO Y. Física para o ensino médio. São Paulo: Saraiva, 2010,
volume 1.
PENTEADO, P. C. M.; TORRES, C. M. A. Física - ciência e tecnologia. São Paulo:
Moderna, 2005, volume 1.
GASPAR, A. Compreendendo a Física, volume 3, Editora Ática , SP , 2010.
HEWITT, P. G. Fundamentos de física conceitual, Editora Bookman, Porto Alegre,
2009.
PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Jardel Santos Cipriano
Tema: MRU
Assunto: Mecânica
1. INTRODUÇÃO
Movimento retilíneo uniforme (MRU) é descrito como um movimento de um
móvel em relação a um referencial, movimento este ao longo de uma reta de forma
uniforme, ou seja, com velocidade constante. Diz-se que o móvel percorreu distâncias
iguais em intervalos de tempo iguais.
2. OBJETIVO
A experiência tem como objetivo representar o movimento retilíneo uniforme.
3. MATERIAIS NECESSÁRIOS

Mangueira transparente, trena;

Seringa, água, arame, durepoxi;

Óleo, cronômetro;

Base de madeira;

Suco para colorir;

Colher;

Recipiente.
4. PROCEDIMENTOS
A montagem da experiência é bem simples, primeiro acoplamos a mangueira a
base de madeira com arame, em seguida fazemos marcações de 5 em 5 cm (você
pode fazer diferente), na própria base de madeira ou em uma folha e colar. A
realização do experimento consiste em colocar óleo dentro da mangueira que está
acoplado na madeira, depois misturamos água com o suco para colorir em uma
vasilha e sugamos um pouco com a seringa, logo após injetamos o material da seringa
dentro da mangueira de forma a fazer uma bolinha, esta vai começar a descer quando
ela passa pelas marcações começamos há marcar o tempo. Anote o tempo que ela
leva para passar de uma marcação até a outra, eles vão ser aproximadamente iguais,
demonstrando assim o movimento retilíneo uniforme.
FIGURA 1 – Mangueira acoplada a base de madeira com óleoe siringa para injetar agua.
4.1 ATIVIDADES PROPOSTAS
a) Complete a tabela:
Espaço (cm)
Tempo (min)
Velocidade (cm/min)
5 cm
10 cm
15 cm
20 cm
b) Construa os gráficos:
A) S x T
B) V x T
5. REFERÊNCIAS
Física Básica. Volume único- Nicolau e Toledo.
Física Básica - Mecânica - 1a. Edição Alaor S. Chaves e José Francisco de Sampaio
Editora LAB, 2007.
Gaspar, Alberto. Física: Mecânica. (volume 1) São Paulo: Ática. 2010.
PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Danilo Capelari
Tema: Atrito
Assunto: Mecânica
1. INTRODUÇÃO
A maior parte das opiniões a respeito da relação entre a força de atrito e a área
de atrito entre um objeto qualquer e uma superfície é: quanto maior a área de contato,
maior a força de atrito. O experimento consiste em algumas caixas de CD puxadas
por um elástico fino de duas formas: na primeira estão espalhadas como um tapete,
na segunda elas estão empilhadas com uma área de contato com a superfície muito
menor que a primeira. Estamos supondo que a distensão do elástico mede a força
aplicada para vencer a força de atrito.
2. OBJETIVO
Mostrar que não há relação entre a força de atrito que age em um objeto e sua
área de contato com a superfície em que desliza.
3. MATERIAIS NECESSÁRIOS

4 caixas de CD, elástico fino, régua;

Fita adesiva, lápis, caneta
4. PROCEDIMENTOS
Coloque as 4 caixas de CD sobre a mesa. Prenda o elástico na primeira caixa.
Complete a estrutura, prendendo as caixas de CD uma atrás da outra. Puxe o elástico
até que ele fique esticado, porém não distendido; faça uma marca nele com a caneta.
Esta marca será seu indicador. Ainda na mesma posição, trace uma reta na mesa na
direção do elástico com o lápis e marque, na reta, qual a posição do indicador no
elástico. Deslize a régua sobre a reta até que ela marque zero centímetro na marca
que você fez na mesa. Puxe o elástico até que o conjunto esteja quase se movendo.
Registre o quanto o elástico esticou. Repita mais algumas vezes e faça uma média
dos valores registrados. Descole a última caixa, dobre a segunda sobre a primeira, e
ponha-a sobre as outras duas. Repita o procedimento de medida anterior e compare
os valores das duas medidas.
Figura 1 – caixas dispostas uma atrás da outra com elástico na primeira
4.1 ATIVIDADES PROPOSTAS
a) Faça uma relação entre a “força” aplicada para colocar o conjunto em movimento e
a disposição dos objetos sobre a mesa.
b) Utilizando algum objeto de massa conhecida, procure relacionar a distensão do
elástico com a força em Newons.
c) Quais os possíveis erros que podemos atribuir às medidas realizadas neste
experimento? O que pode ser feito para minimizá-los?
5. REFERÊNCIAS
RAMALHO; NICOLAU; TOLEDO. Os Fundamentos de Física – Mecânica. São Paulo:
Moderna, 2007
http://www2.fisica.ufc.br/agopin/EXPERIMENTOS.pdf
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Silvio Marcos Pilatti
Tema: Máquina de Atwood
Assunto: Segunda Lei de Newton
1. INTRODUÇÃO
Esse dispositivo, a máquina de Atwood, foi desenvolvido no século XVIII por
George Atwood, para medir a aceleração da gravidade g. Hoje a usamos para
demonstração das leis da dinâmica. Consiste em dois corpos de massa m1 e m2
presos por uma corda que passa sobre uma roldana.
A aceleração de um objeto depende da força resultante aplicada, e a massa.
Na Máquina de Atwood, a diferença de peso entre as duas massas interligadas pelo
fio, determina a força resultante que age no sistema de ambas as massas.
Se for considerada uma corda sem massa e inelástica, e uma polia ideal sem
massa, estando a corda tensionada é equivalente a força peso em m1 estar sendo
aplicada também em m2, e a força peso em m2 estar sendo aplicada também em
m1, disso, usando a Segunda Lei de Newton, pode-se chegar a uma equação para a
aceleração a das massas, como também da aceleração da gravidade g e da tensão
T na corda.
1.1.
ESTUDO ANALÍTICO
Massa total do sistema: mt = m1 + m2 (é o resultado da soma das massas dos
elementos do sistema)
Força resultante aplicada no sistema: FR = (m1g – m2g) = (m1  m2 ) g
Aceleração do sistema: a 
FR (m1  m2 )

g
mt (m2  m1 )
Velocidade final do sistema: V2 = 2ah = 2
Aceleração da gravidade: g =
(m1  m2 )
gh
(m2  m1 )
(m2  m1 )
a
(m1  m2 )
at 2
h

Tempo para percorrer h:
2
Tensão do fio: T = m2a +m2g
;
h
ou
gt 2
2
T = m1a – m1g
2. OBJETIVO
Verificar experimentalmente a 2ª lei de Newton, testando a relação entre força
resultante, massa e aceleração.
3. MATERIAIS NECESSÁRIOS

Uma polia de plástico leve, com eixo e suporte para fixação;

Duas massas de 60g;

Uma massa de 100 g;

Uma massa de 30 g;

Uma massa de 20 g;

1 fio leve e inextensível (linha de pesca) para ser utilizado na polia, em cujas
extremidades possam ser amarradas as massas;

Cronômetro (pode ser do celular);

Trena.
4. PROCEDIMENTOS
a) Faça a montagem da máquina de Atwood como sugere a figura 2, de modo que
as massas fiquem bem conectadas ao fio e o arranjo permaneça contido em um
plano vertical.
b) Pendure as duas massas iguais (60 g) e observe que as massas se mantém em
equilíbrio, independentemente da posição em que foram abandonadas. Isso significa
que elas poderão ser largadas emparelhadas ou com uma abaixo da outa. Seja
como for, permanecerão em repouso nas suas respectivas posições.
c) Coloque sobre uma das massas penduradas outra massa (100 g) e observe que
as massas, uma vez abandonadas, adquirem movimento acelerado, com a mais
leve subindo e a mais pesada descendo.
d) Aumentando ainda mais a diferença das massas, você perceberá que do primeiro
para o segundo caso haverá um aumento perceptível na intensidade da aceleração.
e) Meça a altura h entre a base da massa m1 e a superfície da mesa.
h = _____ m
f) Preencha a tabela abaixo (tabela 1) com os valores teóricos, para o
movimento do sistema.
g) Preencha a tabela abaixo (tabela 2) com os valores experimentais, para o
movimento do sistema.
h) Preencha a tabela abaixo (tabela 3) com a relação entre os valores experimentais
e os valores teóricos, para o movimento do sistema.
i) Variando as massas (use massas diversas), construa o diagrama aceleração versus
variação de massa(Δm).
j) Por que a diferença de massa faz aumentar a intensidade da aceleração?
k) O que ocorre com a intensidade da tração no fio na medida em que se aumenta a
diferença de massa? Aumenta, diminui ou permanece constante? Justifique com
cálculos.
5. REFERÊNCIAS
YAMAMOTO, K.; FUKE, L. F. Física para o ensino médio 1, 3ª Edição.- São Paulo:
Saraiva, 2013.
DOCA, R. H.; BISCUOLA, G. J.; BOA, N. V. Física 1, 2ª Edição - São Paulo: Saraiva,
2013
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos da Física, volume 1:
Mecânica. 8ª. Edição. – Rio de Janeiro: LTC, 2008.
TIPLER, P. – Física. 3ª edição, Vol. 1. Rio de Janeiro, Livros Técnicos e Científicos
Editora S.A. 1995.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Artur José dos Santos Pires
Tema: Uma Demonstração da Lei de Hooke
Assunto: Dinâmica
1. INTRODUÇÃO
Robert Hooke era filho do reverendo John Hooke - religião anglicana - e foi o
penúltimo dos seus quatro filhos.
Robert Hooke teve uma infância muito conturbada, além de seus problemas de
saúde, enfrentava muitas dificuldades financeiras. Seu pai John Hooke suicidou-se
em 1648, deixando ao filho uma quantia de 100 libras, pois, tinha em mente que seu
filho pudesse tornar-se um relojoeiro.
Quando Hooke foi para Londres, levou suas reservas da herança e apresentou
ao Dr. Busby, o reitor da escola, que lhe dedicou grande amizade, constituindo-se em
incentivador constante de sua carreira. Doutor Busby era o melhor amigo de Robert
Hooke, reitor da Universidade de Oxford. Ambos nutriam paixão ardente por Elizabeth
Bernays, empregada doméstica de Busby.
Em 1665 foi nomeado professor de geometria no Gresham College.
Robert Hooke também alcançou fama enquanto principal ajudante de
Christopher Wren na reconstrução que se seguiu ao Grande Incêndio de Londres, em
1666. Trabalhou no Observatório de Greenwich e no Bethlehem Hospital.
Desenho de uma pulga por Hooke, contida no livro Micrographia.
Morreu deixando 9.580 libras e uma pequena propriedade na ilha de Wight. Ao
seu funeral compareceram todos os sócios da Royal Society, em reconhecimento do
seu mérito como cientista. Assim que Hooke morreu, Newton assumiu a Royal Society
e a partir daí não foram encontrados retratos autenticados de Hooke.
2. OBJETIVOS
Buscar o entendimento de cada aluno fazendo com que Lei de Hooke seja
sucinta a qualquer tipo de material, fazendo com isso, venha despertar o senso criativo
de cada aluno para que busque em seu dia a dia a técnica de pesquisa.
3. MATERIAIS NECESSÁRIOS

1 borracha de dinheiro

5 objetos iguais

1 clip

1 rolo de fita adesiva larga

1 régua de 20 cm
4. PROCEDIMENTOS
a) Corte a borracha em uma das dobras.
b) Em uma das extremidades faça um laço bem apertado.
c) Prenda a outra extremidade da borracha com um pedaço de fita adesiva.
d) Coloque na outra extremidade um clip meio aberto em forma de gancho.
e) Coloque o zero da régua alinhado a extremidade superior do clip.
f) A cada objeto colocado faça uma medida e complete a tabela a seguir.
FIGURA 1
FIGURA 2
Nº de
Medida
N/x
Objetos
em X
(objetos/mm)
(N)
(mm)
0
1
2
3
4
Tabela 1
4.1 ATIVIDADES PROPOSTAS
a) Complete o gráfico marcando pontos referente aos pares ordenados.
b) Trace uma reta entre os pontos de forma que a reta passe pelo maior número de
pontos possíveis.
c) O que significa a razão Nº de objetos/x?
d) Obedecendo as regras da álgebra poderia dizer qual tipo da função gerada?
e) Observando posso substituir a borracha de dinheiro por uma mola pode-se produzir
o mesmo efeito que a borracha de dinheiro produzir?
f) Através das medidas obtidas pode-se estimar a quantidade de objetos pendurado
na mola quando a distensão da borracha for 24mm?
g) Ao invés de usar objetos se utilizássemos massas graduadas em g como ficaria a
unidade de medida?
h) Como se pode comparar este evento produzido por uma borracha a um
equipamento que muitas pessoas utilizam no dia-a-dia. Como se chama este
equipamento?
i) Por que este equipamento não é um medidor preciso para vários sistemas
referenciáveis diferentes, quando se trata de quantidade de matéria?
5. REFERÊNCIAS
HALLIDAY, D; RESNICK, R. Fundamentos de Física. 8ª edição, Vol. 01. Rio de
Janeiro: Livros Técnicos e Científicos, 2008.
TIPLER, P.A. Física. Vol.1. Rio de Janeiro: Livros Técnicos e Científicos, 1995.
Wikipédia, a enciclopédia livre. https://pt.wikipedia.org/wiki/Robert_Hooke acessado
em 20/06/2015.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Danilo Capelari
Tema: Construção de um termoscópio
Assunto: Termologia
1. INTRODUÇÃO
Registros dizem que a primeira tentativa de medir temperatura foi feita
por Claudius Galenus em 170 d. C., ele sugeriu uma escala com 4 graus acima e 4
graus abaixo de um neutro, sendo o máximo grau a água fervendo, o mínimo o gelo e
o neutro uma mistura equilibrada dos dois. Galileu inventou em 1592, o primeiro
aparelho para medir uma temperatura, o termoscópio, mas não havia uma escala
definida, o aparelho servia para comparar temperaturas. Vale lembrar que as escalas
termométricas atuais não tinham sido invetadas ainda. A escala Fahrenheit foi
inventada em 1724, a escala Celsius em 1742 e a escala Kelvin em 1848. Com a
criação do termoscópio de Galileu, vieram vários outros aparelhos de medição de
temperatura em seguida. Seu próprio trabalho com o termoscópio fez com que Galileu
desenvolvesse uma concepção essencialmente atômica de calor, publicada em seu
livro Il Saggiatore em 1623.
2. OBJETIVO
Verificar, através de uma coluna de água, qualitativamente a dilatação do gás
atmosférico dentro de uma garrafa por meio da variação da temperatura interna.
3. MATERIAIS NECESSÁRIOS

Garrafa de plástico (PET) de 250 ml

50 cm de mangueira transparente, 5 mm de diâmetro, ( por exemplo de aquário);

Régua graduada de 1m ou trena;

Água;

Tinta guache, corante ou suco;

Pistola e cola quente ou super-cola.
4. PROCEDIMENTOS

Passe 50 cm de mangueira através de um furo na tampa, com diâmetro pouco
menor que o da mangueira. Use cola quente (ou supercola) para vedar a
mangueira na tampa.

Despeje água misturada com tinta guache na garrafa (cerca de 1/4 do seu volume).

Coloque a tampa na garrafa e aperte a bem, de modo que a ponta da mangueira
fique submersa.
Figura 01 - termoscópio

Introduza o termoscópio na mistura água e gelo por dois minutos.

Apalpe bem a parte superior da garrafa com as duas mãos (temperatura das mãos,
30 oC) ou introduza em água à temperatura conhecida (recomenda-se no máximo
30 oC) e mantenha até que a água pare de subir, anote a altura em relação à altura
inicial do banho a 0 oC.

Com a altura inicial e a final e os dois valores de temperatura construa uma relação
entre a temperatura Tc e a altura h.
Figura 02 – modelo de montagem da escala
(Tc - T1)/(T2-T1 )= (h-h1)/(h2-h1)
4.1 ATIVIDADES PROPOSTAS
1) Introduza o termoscópio em uma mistura da água gelada com a água a 30
graus e através da altura da coluna determine a temperatura da mistura, confira
com um termômetro e discuta o resultado.
2) Deixe o termoscópio no ambiente e calcule a temperatura, confira com o
termômetro e discuta o resultado.
3) Quais os possíveis erros que podemos atribuir às medidas realizadas neste
experimento? O que pode ser feito para minimizá-los?
5. REFERÊNCIAS
VALADARES, E. C. Física mais que divertida. 2o ed. Belo Horizonte: Ed. UFMG,
2002.
RAMALHO; NICOLAU E TOLEDO. Os fundamentos da Física: Vol.2. 7a ed. São
Paulo: Moderna, 2001
HALLIDAY; RESNICK E WALKER. Fundamentos de Física. Ed. 6ª. Rio de Janeiro:
LTC, 2002. Vols. 2.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Elissandra Beneti Cateli Mangolin
Tema: Mapeamento de superfícies equipotenciais
Assunto: Eletrostática
1. INTRODUÇÃO
Uma maneira conveniente de introduzir a configuração dos campos elétricos
é dada pelas linhas de força. Este conceito foi introduzido no século XIX por Michael
Faraday (1791–1867), que imaginava o espaço ao redor de um corpo carregado como
sendo preenchido por linhas de força. Embora não tenham significado físico real, tais
linhas, atualmente denominadas Linhas de Campos Elétricos, fornece um modo
conveniente de se visualizar a configuração dos campos elétricos.
Entre dois pontos de uma mesma linha de campo elétrico, existe sempre uma
diferença de potencial elétrico (ddp). Mas pode-se ter dois ou mais pontos, cada um
em linhas diferentes, que estejam ao mesmo potencial elétrico. O conjunto destes
pontos forma uma linha equipotencial. A “família” das linhas equipotenciais constitui
uma superfície equipotencial, que é o lugar geométrico dos pontos que possuem o
mesmo potencial elétrico. Através da propriedade do perpendicularismo entre as
linhas de campo e as linhas equipotenciais (Fig.1), as quais se obtêm em laboratório,
pode-se chegar a uma visualização geral do campo elétrico num plano de uma região
do espaço.
Figura 1 - Esboço das linhas equipotenciais e das linhas de força observadas para três distribuições
de carga: a) carga pontual positiva, b) duas cargas pontuais de mesma intensidade, uma positiva e
outra negativa, c) duas cargas pontuais positivas de mesma intensidade.
Fonte: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=33526
2. OBJETIVOS

Mapear as superfícies equipotenciais de diferentes eletrodos e traçar as linhas
de campos elétricos.
3. MATERIAIS UTILIZADOS

Cuba de acrílica;

Dois fios com “pino banana”;

Água de torneira (comum);

Dois eletrodos em forma de cilindro;

Dois eletrodos em forma de barra plana (Placa Metálica);

Fonte de tensão contínua variável: 0-30 V;

Multímetro;

Quatro folhas de papel milimetrado.
4. PROCEDIMENTOS
4.1 – ELETRODOS PONTUAIS: Sinais Contrários
a) Colocar a folha de papel milimetrado sob a cuba acrílica, Fig.3.2 (a);
b) Ajustar os eletrodos (pontuais) no recipiente, transferindo suas coordenadas para
o papel milimetrado;
c) Despejar uma fina camada de água na cuba acrílica, distribuindo-a uniformemente;
d) Ligar os eletrodos à fonte de tensão e em seguida ajustar a fonte em 10 V (volts);
e) Colocar a ponta de prova fixa em um ponto situado em um dos eletrodos;
f) A ponta de prova móvel, deve ser posicionada a 2 (dois) centímetros da linha
central e movimentada paralelamente a linha procurando uma posição em que a
leitura do voltímetro tenha o mesmo valor;
g) Em seguida, marcar as coordenadas desta posição no papel milimetrado;
h) Repita o procedimento (e)–(g) variando a distância da linha central de 2 cm em 2
cm a direita e a esquerda da linha central. Obs.: 4 (quatro) pontos para cada lado.
i) Repita o procedimento para cada um dos pontos marcados no papel milimetrado
sob a cuba acrílica;
j) Traçar as superfícies equipotenciais e as linhas de campo elétrico.

Os pontos marcados no papel milimetrado, sob a cuba acrílica, devem ser
usados para fixar a ponta de prova fixa.
FIGURA 2 – Montagem com eletrodos pontuais: sinais contrários.
4.2 – ELETRODOS EM FORMA DE BARRA
a) Trocar os eletrodos pontuais por eletrodos em forma de barra, Fig.3.3;
a) Repita os procedimentos do item A;
b) Traçar as superfícies equipotenciais e as linhas de campo elétrico em um papel
milimetrado.
4.3 – PERTURBAÇÃO DO CAMPO ELÉTRICO
a) Repita os procedimentos do item B com uma argola no centro dos eletrodos em
forma de barra;
b) Traçar as superfícies equipotenciais e as linhas de campo elétrico em um papel
milimetrado.
FIGURA 3 – Montagem com eletrodos pontuais: sinais contrários.
4.4 – ATIVIDADES PROPOSTAS
a) Nos papeis milimetrados, trace as superfícies equipotenciais.
b) Nos mesmos papeis, trace agora o campo elétrico indicando por setas ↑, o seu
sentido em cada ponto da superfície equipotencial.
c) Justifique o fenômeno observado no procedimento PARTE 2 item C.
d) As linhas do campo elétrico nunca se cruzam. Por quê?
e) O campo elétrico e o potencial elétrico são campos escalares ou vetoriais?
Justifique.
5. REFERÊNCIAS
FILHO, José Higino; Mapeamento de linhas equipotenciais e de linhas de força do
campo
elétrico
utilizando
uma
cuba
eletrolítica.
Disponível
em:
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=33526. Acesso em
24 de junho de 2015.
ROTEIROS DE FÍSICA; Mapeamentos Equipotenciais, Disponível em:
http://www.pucgoias.edu.br/ucg/prograd/graduacao/ArquivosUpload/43/file/Mapeame
nto%20de%20Superf%C3%ADcies%20Eq%C3%BCpotenciais%20e%20Campos%2
0El%C3%A9tricos.pdf. Acesso em 24 de junho de 2015.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Geislana Padeti Ferreira Duminelli
Tema: Gaiola de Faraday
Assunto: Eletrostática
1. INTRODUÇÃO
Para eletrizar um condutor não é preciso submeter toda sua superfície ao
processo de eletrização. Basta expor uma região e será possível eletrizar todo o
condutor. Isso acontece porque há uma distribuição das cargas ao longo do condutor,
por causa dos elétrons livres, que podem se movimentar em qualquer direção ao longo
de toda a estrutura de um condutor.
A causa dessa movimentação de elétrons é a força eletrostática. A
movimentação ocorre para deixar o interior do condutor com carga nula e,
consequentemente, realocar todo o excesso de carga na superfície externa. Se o
condutor estiver eletrizado negativamente, o saldo de elétrons se concentrará em sua
superfície. Se, por outro, lado, cargas negativas forem removidas e o condutor ficar
eletrizado positivamente, alguns elétrons sairão da superfície e se concentrarão no
centro do condutor tentando deixa-lo com carga nula, causando, assim, um excesso
de cargas positivas em sua superfície.
Em um condutor eletrizado, em situação de equilíbrio, o excesso de cargas fica
distribuído por sua superfície.
Um condutor, quando carregado, tende a espalhar suas cargas uniformemente
por toda a sua superfície. Se esse condutor for uma esfera oca, por exemplo, as
cargas irão se espalhar pela superfície externa, pois, a repulsão entre as cargas fazem
com que elas se mantenham o mais longe possível umas das outras. Os efeitos de
campo elétrico criados no interior do condutor acabam se anulando, obtendo assim
um campo elétrico nulo. O mesmo acontece quando o condutor não está carregado,
mas está em uma região que possui um campo elétrico causado por um agente
externo. Seu interior fica livre da ação desse campo externo, fica blindado. Esse efeito
é conhecido como blindagem eletrostática. Para provar esse efeito, o físico britânico
Michael Faraday fez, em 1836, um experimento para provar os efeitos da blindagem
eletrostática. Ele construiu uma gaiola de metal carregada por um gerador
eletrostático de alta tensão e colocou um eletroscópio em seu interior para provar que
os efeitos do campo elétrico gerado pela gaiola eram nulos. O próprio Faraday entrou
na gaiola para provar que seu interior era seguro. Esse experimento ficou conhecido
por “Gaiola de Faraday”.
Assim, a blindagem eletrostática também ficou conhecida por gaiola de Faraday
e esse efeito é muito utilizado em nosso dia a dia. Como exemplos podemos citar os
carros e aviões, que atuam como gaiolas de Faraday, nos protegendo caso sejamos
atingidos por uma descarga elétrica, contrariando o pensamento popular de que os
pneus do carro é que fazem essa proteção. Construções também são feitas utilizando
blindagem eletrostática, a fim de proteger equipamentos eletrônicos. Essa blindagem
pode ser vista facilmente, para isso pegue um celular ou um rádio ligado e embrulheo em papel alumínio. O alumínio vai agir como a gaiola de Faraday, o celular e o rádio
poderão perder o sinal.
2. OBJETIVOS
a) Observar fenômenos envolvendo campos elétricos, como interação a distância
e blindagem eletrostática.
b) Entender o funcionamento e desenvolver uma blindagem eletrostática por meio
da gaiola de Faraday.
3. MATERIAIS NECESSÁRIOS

Papel alumínio

Caixa pequena papel ou madeira

Celular ligado
4. PROCEDIMENTOS
a) Envolver a caixa com o papel alumínio sem deixar nenhum espaço
desencapado, conforme a figura 1.
FIGURA 1 – Caixa sendo envolvida com o papel alumínio
b) Deixar o celular ligado e sintonizado em uma frequência de rádio, conforme
a figura 2.
FIGURA 2 – Celular sintonizado em uma frequência de rádio
c) Colocar o celular dentro da caixa e fechá-la, conforme figura 3.
FIGURA 3 – Caixa envolvida com papel alumínio fechada
d) Observar o sinal sonoro emitido pelo celular.
e) Retirar o celular de dentro da caixa e observar o fenômeno.
4.1 ATIVIDADES PROPOSTAS
1) Se esse experimento for realizado com uma folha de sulfite em vez de papel
alumínio, o resultado será o mesmo? Justifique sua resposta.
2) Deduza a relação existente entre o telefone celular e o campo elétrico.
3) Por que geralmente perdemos o sinal do celular quando estamos dentro do
elevador?
4) Carros e aviões são exemplos de grandes gaiolas de Faraday, impedindo que
as pessoas que estão em seu interior recebam uma descarga elétrica
provenientes de raios. Alguns equipamentos eletrônicos também possuem
essa blindagem eletrostática. Descreva o processo de blindagem de um
condutor.
5. REFERÊNCIAS
Válio, Adriana Benetti; Ferdinian, Bassam; Ser protagonista: física 3: ensino médio –
1ed. São Paulo: Edições SM, 2009.
http://www.mundoeducacao.com/fisica/gaiola-faraday.htm, acesso em 16 de junho de
2015.
http://www.manualdomundo.com.br/2014/02/como-fazer-gaiola-de-faraday/,
em 16 de junho de 2015.
acesso
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Washington Roberto Lerias
Tema: Associação de Capacitores
Assunto: Eletrostática
1. INTRODUÇÃO
Praticamente os experimentos propostos consistem em utilizar 3 capacitores da
ordem de µF e associá-los em série, em paralelo e de forma mista, tanto na placa
protoboard tanto quanto no proteus, verificar e comparar a teoria com a prática tanto
no que diz respeito a capacitância equivalente, quanto à carga, energia, diferença de
potencial e corrente elétrica totais bem como em cada componente do circuito.
1.1 CAPACITOR
O capacitor é um dispositivo que armazena cargas elétricas Q em placas
metálicas paralelas, separadas por um material isolante ou dielétrico (fig.1).
Fig.1 - Componentes de um capacitor
Quando posto em uma diferença de potencial U,(fig.2) as cargas elétricas
negativas "sentem" a presença do potencial positivo, ou seja são atraídos conforme a
lei de Coulomb e esses se movimentam em direção às placas metálicas, já que são
os elétrons que se movimentam na superfície dos condutores, que como não têm
como atravessar o material isolante, ali se acumulam. Como uma das placas fica com
excesso de elétrons, por repulsão, elas afastam os elétrons da outra placa, deixando
a sua superfície com o mesmo acúmulo de cargas positivas, que são os próprios
prótons que formam a sua estrutura metálica. Quando o circuito é fechado, as cargas
acumuladas se descarregam rapidamente gerando um pico de corrente elétrica muito
útil para vencer a inércia de motores interligados a grandes massas como por exemplo
motores de portões eletrônicos, máquina de lavar roupa, entre outros.
Fig.2 - Princípio de funcionamento de um capacitor em circuito simples.
Em um circuito elétrico, considerando um capacitor eletrolítico, a figura 2 acima fica
assim determinada (fig.3):
Fig.3 - Esquema de circuito simples com capacitor polarizado
Quanto maior a diferença de potencial aplicada, maior será a quantidade de carga
armazenada em um capacitor, logo temos:
em homenagem ao cientista britânico Michael Faraday (1791 — 1867)
Onde C é chamada de Capacitância e que significa a quantidade de carga que o
capacitor armazena por unidade de tensão.
1.2
ASSOCIAÇÃO DE CAPACITORES EM SÉRIE:
Fig.4 - Esquema de circuito em série
Neste caso cada capacitor está submetido a uma diferença de potencial, tal que
na somatória obtém-se a diferença de potencial total do circuito e a carga total do
circuito fica sendo a mesma para todos os capacitores (Q=Q1=Q2=Q3=....=QN),onde N
é o número de capacitores. Logo:
Invertendo os dois lados da equação obtém-se:
1.3
ASSOCIAÇÃO DE CAPACITORES EM PARALELO:
Fig.5 - Esquema de circuito em paralelo
Já neste caso, todos os capacitores estão ligados na mesma diferença de
potencial (U=U1=U2=U3=...=UN) e cada capacitor se carrega individualmente de tal
maneira que a carga total do circuito é o somatório das cargas de todos os
capacitores em paralelo. Utilizando a equação da capacitância tem-se:
e como as tensões são iguais, têm-se como a capacitância equivalente do circuito
em paralelo:
1.4 CÁLCULO DA ENERGIA POTENCIAL ELÉTRICA( Ep)TRANSFERIDA PARA
O CAPACITOR:
Para calcular a energia dispensada para carregar as placas de um capacitor,
pode-se imaginar que a carga total Q foi transferida em pequenas cargas infinitesimais
dq desde uma das armaduras até a outra. Cada vez que uma carga dq passa da
armadura negativa para a positiva, ganha uma energia potencial elétrica Ep:
A energia total armazenada no capacitor obtém-se por integração, de q = 0 até q =
Q (área sob a reta no gráfico de U em função de q, na figura 6)
Fig.6 - Gráfico de U em relação a q
2. OBJETIVO
Os experimentos sugeridos têm como objetivo verificar as relações entre as
grandezas envolvidas no estudo das associações em série, em paralelo e mista de
capacitores, tanto na prática quanto em simulação. Serão montados circuitos de
ambos os tipos em protoboard e simulados no proteus, aproveitando o conhecimento
que a turma já tem destas ferramentas, bem como será feita analise e medida da
capacitância resultante, energia, tensão, corrente e carga em cada elemento e totais.
3. MATERIAIS NECESSÁRIOS

Capacitores diferentes, da ordem de µF

Protoboard

Fonte de tensão - 20V


Multímetro
Programa Proteus
4. PROCEDIMENTOS
4.1
EXPERIMENTO E SIMULAÇÃO
4.1.1
MONTAGEM DO CIRCUITO EM SÉRIE
Primeiramente executar a montagem do circuito em série com os 3 capacitores da
ordem de µF escolhidos, conforme exemplo abaixo:
Fig.7 - Circuito em série com 3 capacitores

Calcular a Capacitância equivalente do circuito;

Calcular a carga armazenada;

Medir e calcular a diferença de potencial em cada capacitor;

Utilizar estas medidas para calcular a carga armazenada nos capacitores;

Calcular a energia potencial em cada capacitor e a total do circuito;

Observar o comportamento da corrente elétrica quando o circuito é ligado e
medir a corrente elétrica máxima observada no multímetro;

Anotar os valores encontrados na tabela abaixo:
Capacitor
C
Q
U
U
Q
Medida
Calculada
A partir de U
medida
Ep
i
1
2
3
Total

Montar o mesmo circuito no proteus, conforme modelo da figura 8, rodar o
programa e comparar com os valores da tabela.
Fig.8 - Circuito em série rodado no proteus
4.1.2
MONTAGEM DO CIRCUITO EM PARALELO
Agora repetir o experimento, porém com os 3 capacitores escolhidos
ligados em paralelo exemplificado no circuito abaixo (fig.9):
Fig.9 - Circuito em paralelo com 3 capacitores

Calcular a Capacitância equivalente do circuito;

Calcular a carga armazenada;

Medir e calcular a diferença de potencial em cada capacitor;

Utilizar estas medidas para calcular a carga armazenada nos capacitores;

Calcular a energia potencial em cada capacitor e a total do circuito;

Observar o comportamento da corrente elétrica quando o circuito é ligado e
medir a corrente elétrica máxima observada no multímetro;

Anotar os valores encontrados na tabela abaixo:
Capacitor
C
Q
U
U
Q
Medida
Calculada
A partir de U
medida
Ep
i
1
2
3
Total

Montar o mesmo circuito no proteus, conforme modelo abaixo (fig.10), rodar o
programa e comparar com os valores da tabela.
Fig.10 - Circuito paralelo rodado no proteus
4.1.3
MONTAGEM DAS ASSOCIAÇÕES MISTA DE CAPACITORES
Agora faremos mais duas combinações com os 3 capacitores escolhidos
formando associações mistas conforme esquemas abaixo (fig.11):
Fig.11 - Arranjos de circuitos mistos com os 3 capacitores
A dica para achar a capacitância equivalente dos circuitos acima é a mesma para
associações mistas de resistores, ou seja, quando a série está fora do paralelo,
resolve-se primeiro em paralelo e depois em série. E quando a série estiver
dentro do paralelo, resolve-se primeiro em série e depois em paralelo.

Calcular a Capacitância equivalente do circuitos;

Calcular a carga armazenada;

Medir e calcular a diferença de potencial em cada capacitor;

Utilizar estas medidas para calcular a carga armazenada nos capacitores;

Calcular a energia potencial em cada capacitor e a total do circuito;

Anotar os valores encontrados na tabela abaixo:
Primeiro Caso:
Capacitor
1
2
3
Total
C
Q
U
U
Q
Medida
Calculada
A partir de
U medida
Ep
Segundo Caso:
Capacitor
C
Q
U
U
Q
Medida
Calculada
A partir de U
medida
1
2
3
Total
Reproduzir os circuitos no proteus e comparar resultados:
Ep
Fig.12 - Arranjos de circuito misto rodado no proteus
4.2
QUESTÕES:

Como você faria para que os capacitores demorassem mais para se
carregar?
___________________________________________________________________
___________________________________________________________________

Qual circuito consome mais energia?
___________________________________________________________________

Qual circuito apresentou maior capacitância?
___________________________________________________________________

Como você explica o fato de que 2 capacitores diferentes obtiveram a mesma
diferença de potencial no circuito em série?
___________________________________________________________________
___________________________________________________________________
__

Como você explica o fato de que 2 capacitores diferentes obtiveram a mesma
corrente no circuito em paralelo?
___________________________________________________________________
___________________________________________________________________
__

Quais foram as maiores dificuldades que você enfrentou para realizar este
experimento?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___

Como você faria para medir a capacitância de cada capacitor?
___________________________________________________________________
___________________________________________________________________
__
5. REFERÊNCIA
HALLIDAY, David. RESNICK, Robert. WALKER, Jearl. Fundamentos de Física 3 Eletromagnetismo - Editora: LTC 9ª Ed. 2012.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO
PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Joslaine de Lima
Tema: Bateria com Forminha de Gelo
Assunto: Eletrodinâmica
1. INTRODUÇÃO
Apresenta-se neste roteiro a construção de pilhas eletroquímica simples,
utilizando-se de materiais facilmente encontrados no mercado a um baixo custo. Com
materiais simples e atóxicos, o docente pode dispor de um dispositivo portátil e de
fácil manuseio, sendo capaz de produzir vários destes geradores químicos para que
os alunos possam manuseá-los dentro da sala de aula. Esta bateria normalmente é
de grande utilidade didática no ensino. Para o de física, por exemplo, ao tratar-se de
tópicos como corrente elétrica ou circuitos elétricos. E no ensino de química, por
exemplo, pode se lecionar reações químicas, tais como a oxidação de diversos
metais. De maneira geral, pode ser igualmente útil em outros experimentos que
requeiram a utilização de corrente elétrica continua
2. OBJETIVOS
Construir uma bateria de baixo custo com materiais simples e de fácil acesso
para acender um led.
3. MATERIAIS NECESSÁRIOS

1 forminha de gelo com capacidade para 14 cubos de gelo

1 led

13 parafusos ( 1 parafuso a menos que a quantidade de cubos da forminha)

Fio de cobre

Sal

Água
4. PROCEDIMENTOS
a) Descascar os fios de cobre e cortar em pedaços com o dobro do tamanho do
parafuso.
b) Amarrar o fio no parafuso formando um V entre o parafuso e o fio de cobre
conforme a figura 1.
Figura 1- Fio de cobre amarrado no parafuso em “V”
4.1 CARREGANDO A BATERIA
a) Uma pitada de sal em cada cubo de gelo da forminha.
b) Preencher com a água, cuidando para não transbordar conforme a figura 2.
Figura 2 – Como preencher com água a forminha.
c) Colocar os parafusos nos buracos da forminha intercalando cabeça em um
buraco e o cobre em outro conforme a figura 3, (observação não deixar
encostar o cobre de um conjunto no parafuso de outro conjunto).
Figura 3 – Montado o circuito
d) Primeiro é necessário testar se a bateria está funcionando, com um
voltímetro posicionado conforme a figura 4, mede-se a tensão na bateria.
Figura 4 – Teste da bateria
e) Para acender o led, este devera ser posicionado de maneira que feche o
circuito conforme a figura 5:
Figura 5 – acendendo o led
4.2 ATIVIDADES PROPOSTAS
1) De onde vem a energia elétrica que acende o led?
2) Essa bateria dura pra sempre?
3) Porque tantos parafusos e alocados nessa posição na forminha?
5. REFERÊNCIAS
OLIVEIRA. Alessandro. Construção de uma pilha didática de baixo custo.
Disponível em: https://periodicos.ufsc.br/index.php/fisica/article/viewFile/6693/6160.
Acesso em 15 de jun. 2015.
TENÓRIO. Iberê. A bateria mais simples do mundo: Bateria com forminha de
gelo. Disponível em:
<https://www.youtube.com/watch?v=19YS4KuiK_w&list=LLIT0gJD-TO1xKseBCWOV5w&index=4> Acesso em 15 de jun. 2015.
PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Danilo Corci Batista
Tema: Aprendendo a utilizar o código de cores
Assunto: Eletrodinâmica
1. INTRODUÇÃO
Resistor é um dispositivo eletrônico que apresenta como funções principais:
transformar energia elétrica em energia térmica (Efeito Joule) e dificultar a passagem
de corrente elétrica. Entende-se à dificuldade que o resistor apresenta a essa
passagem de corrente como sendo sua resistência elétrica. Classificamos os
resistores em dois tipos: fixos e variáveis.
Os resistores fixos são aqueles cujo valor da resistência não pode ser alterada,
enquanto que os variáveis tem sua resistência modificada dentro de uma faixa de
valores através de um cursor móvel (potenciômetro ou reostato).
Figura 1 : Resistor fixo
Figura 2: Potenciômetros
Figura 3: Reostato
Os resistores fixos são especificados por três parâmetros: o valor nominal da
resistência elétrica, a tolerância e máxima potência elétrica dissipada. O valor de um
resistor fixo pode ser facilmente identificado de acordo com as cores que apresenta
na cápsula que envolve o material resistivo, ou então usando um ohmímetro, que será
discutido posteriormente.
Os valores das resistências dos resistores podem ser reconhecidos pelas cores
das faixas em suas superfícies, cada cor e sua posição no corpo do resistor
representa um número, de acordo com o seguinte esquema:
1.1 APRENDENDO A IDENTIFICAR A RESISTÊNCIA DO RESISTOR
O valor da resistência é obtido de acordo com a ordem que aparece as cores
das faixas. Os dois primeiros algarismos são representados pelas cores da primeira e
segunda faixa, a cor da terceira faixa indica o expoente da potência de 10 que deve
ser multiplicado pelo número formado pelos algarismos citados anteriormente (ou
seja, é a quantidade de zeros), e a cor da quarta faixa informa a tolerância.
1.2 TABELA DE CORES
Tabela 1: Código de cores para resistores
2. OBJETIVO
Fazer a leitura do valor nominal da resistência elétrica de cada resistor
utilizando o código de cores.
3. MATERIAIS NECESSÁRIOS

10 resistores
4. PROCEDIMENTOS
a) Com o auxílio do código de cores faça a leitura da resistência elétrica de cada
resistor e anote na tabela 2, assim como apresentado no exemplo na primeira
linha da tabela.
Tabela 2 – Valores lidos
4.2 ATIVIDADES PROPOSTAS
1. De acordo com o código de cores complete o quadro abaixo com as cores
correspondentes as faixas que representam o valor da resistência e a
tolerância.
5. REFERÊNCIAS
BATISTA, M.C.; FUSINATO, P.A., Eletricidade Básica – Caderno de Atividades
Experimentais, 1ª Edição 2014 p. 15 Editora Massoni – Maringá - PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Artur José dos Santos Pires
Tema: Associação De Resistores Em Série
Assunto: Eletrodinâmica
1. INTRODUÇÃO
A Lei de Ohm, assim designada em homenagem ao seu formulador, o físico
alemão Georg Simon Ohm (1787-1854), afirma que, para um condutor mantido à
temperatura constante, a razão entre a tensão entre dois pontos e a corrente elétrica
é constante. Essa constante é denominada de resistência elétrica.
2. FUNDAMENTAÇÃO TEÓRICA
2.1.
PRIMEIRA LEI DE OHM
Quando essa lei é verdadeira num determinado condutor mantido à
temperatura constante, este denomina-se condutor ôhmico. A resistência de um
dispositivo condutor é dada pela fórmula:
𝑅=
𝑈
𝑖
ou 𝑈 = 𝑅𝑖
Em que:
U é a diferença de potencial elétrico (ou tensão, ou d.d.p.) medida em volt (V);
i é a intensidade da corrente elétrica medida em ampère (A) e
R é a resistência elétrica medida em ohm (Ω).
Essa expressão não depende da natureza de tal condutor: ela é válida para
todos os condutores. Para um dispositivo condutor que obedeça à lei de Ohm, a
diferença de potencial aplicada é proporcional à corrente elétrica, isto é, a resistência
é independente da diferença de potencial e da corrente. Um dispositivo muito utilizado
em aparelhos eletrônicos, como rádios, televisores e amplificadores, que obedece à
essa lei é o resistor, cuja função é controlar a intensidade de corrente elétrica que
passa pelo aparelho.
Entretanto, para alguns materiais, por exemplo os semicondutores, a
resistência elétrica não é constante, mesmo que a temperatura seja, ela depende da
diferença de potencial U. Estes são denominados condutores não ôhmicos. Um
exemplo de componente eletrônico que não obedece à lei de Ohm é o diodo.
2.2.
INTERPRETAÇÃO DA RESISTÊNCIA ELÉTRICA
A resistência elétrica pode ser entendida como a dificuldade de se estabelecer
uma corrente elétrica num determinado condutor. Por exemplo, um fio de nicromo
precisa ser submetido à uma diferença de potencial elétrico de 300 V para que seja
estabelecida uma corrente de 1 A, enquanto um fio de tungstênio precisa ser
submetido à apenas 15 V para que nele se estabeleça a mesma corrente. Isto significa
que a resistência elétrica do nicromo é maior do que a do tungstênio:
𝑅𝑛𝑖𝑐𝑟𝑜𝑚𝑜 =
300𝑉
= 300Ω
1𝐴
𝑅𝑡𝑢𝑛𝑔𝑠𝑡ê𝑛𝑖𝑜 =
2.3.
15𝑉
− 15Ω
1𝐴
SEGUNDA LEI DE OHM
A segunda lei de Ohm diz que a resistência elétrica de um condutor homogêneo
e de seção transversal constante é proporcional ao seu comprimento 𝓁, inversamente
proporcional à sua área transversal A e depende da temperatura e do material de que
é feito o condutor:
𝑅=
𝜌𝓁
A
A grandeza ρ chama-se resistividade elétrica e é característica do material e da
temperatura. Sua unidade de medida é o ohm-metro (
m). Ela é inversamente
1
proporcional condutividade elétrica(𝜌 = 𝜎).
2.4.
FORMULAÇÃO MICROSCÓPICA
Em um condutor metálico isolado, os elétrons estão num estado de movimento
aleatório, não apresentando deslocamento preferencial, em média, em nenhuma
direção. Se este condutor tem seus terminais ligados aos de uma bateria, um campo
elétrico E é criado em todos os pontos no interior do condutor e atua sobre os elétrons
de forma a produzir um movimento de arrasto, que é a corrente elétrica. Em
condutores ôhmicos, o vetor densidade de corrente elétrica, J cujo módulo é igual à
corrente elétrica dividida pela área de seção transversal, i/A (quando a corrente é
uniformemente distribuída pelo condutor), é proporcional ao campo elétrico E. O fator
de proporcionalidade entre a densidade de corrente e o campo elétrico é a
condutividade elétrica σ:
𝐽 = 𝜎𝐸
Esta é a relação microscópica equivalente à relação macroscópica 𝑈 = 𝑅𝑖.
Pode-se dizer também que um material condutor obedece à lei de Ohm se a
condutividade
for independente de E e de J.
A unidade de medida da condutividade é o Siemens por metro (S/m). Materiais
que conduzem melhor a corrente elétrica são aqueles que possuem os valores mais
altos de σ. A prata, o cobre e o alumínio, por exemplo, são bons condutores, enquanto
a mica e o vidro são maus condutores.
2.5.
A RELAÇÃO MACROSCÓPICA DA LEI DE OHM A PARTIR DA RELAÇÃO
MICROSCÓPICA
Fio de comprimento 𝓁 e área transversal A percorrido por uma corrente elétrica
i na presença de um campo elétrico E.
A relação macroscópica 𝑈 = 𝑅𝑖 pode ser obtida da relação microscópica 𝑱 =
𝝈𝑬 a partir do seguinte exemplo.
Considere um segmento de fio condutor de comprimento 𝓁 e seção reta A, com
uma corrente i. Para que o campo elétrico não varie apreciavelmente, o segmento do
fio deve ser muito pequeno. Sendo o campo elétrico dirigido da esquerda para a
direita, o potencial é mais baixo neste lado do que no outro, de forma que se tem
𝑈 = 𝑈𝑒 − 𝑈𝑑 = 𝐸𝑙
onde E é o módulo do campo elétrico. A corrente no condutor é igual ao produto da
densidade de corrente pela área de seção reta:
𝑖 = 𝐽𝐴 = 𝜎𝐸𝐴 =
𝜎𝐴𝑈
𝑙
onde usou-se a lei de Ohm na forma microscópica na passagem anterior. Sendo
assim,
𝑈=
𝑙
𝜎𝐴
substituindo σ por 1/𝜌, obtém-se:
𝜌𝑙
𝑈 = ( )𝑖
𝐴
A expressão entre parênteses pode ser definida como:
𝑅≡𝜌
𝑙
𝐴
e, então, obtém-se a relação
𝑈 = 𝑅𝑖
2.6.
VARIAÇÃO DA RESISTIVIDADE COM A TEMPERATURA
Nos metais, os elétrons da última camada eletrônica estão fracamente ligados
a átomos individuais, podendo mover-se livremente. Quando a temperatura aumenta,
a amplitude do movimento dos íons da rede cristalina também aumenta, o que dificulta
a locomoção dos elétrons livres. Em outras palavras, isto quer dizer que a resistividade
aumenta com a temperatura. Para uma ampla gama de substâncias, esse aumento é
linear, dentro de uma larga faixa de temperaturas. Isto pode ser descrito pela seguinte
equação:
𝜌 = 𝜌0 [1+∝ (𝑇 − 𝑇0 )
onde:
𝜌 é a resistividade final à temperatura T,
𝜌0 0 é a resistividade inicial à temperatura T0 e
∝ é o coeficiente de temperatura da resistividade e é positivo para os metais.
Nos semicondutores a resistividade diminui com o aumento da temperatura.
Isto acontece, porque as flutuações térmicas a altas temperaturas provocam a
promoção de elétrons ligados a transportadores de carga livres.
A resistividade de alguns condutores desaparece bruscamente abaixo de uma
temperatura crítica, quando estes são resfriados, podendo manter uma corrente por
muito tempo sem necessidade do uso de baterias. Esse fenômeno é chamado de
supercondutividade e foi divulgado pela primeira vez em 1911 pelo físico holandês
Heike Kamerlingh Onnes.
2.7.
CIRCUITOS DE RESISTORES EM SÉRIE
Em um circuito eletrico em série temos que o resistor equivalente é dado pela
soma das reistências internas de cada resitor ou seja: 𝑅𝑒𝑞 = 𝑅1 + 𝑅2 + ⋯ + 𝑅𝑁
No circuito em série a corrente elétrica em cada resistor é sempre constante
para todos os resitores.
A tensão elétrica que passa no circuito elétrico é sempre igual soma da tensão
que percorre cada reistor, ou seja: 𝑈𝐴𝐵 = 𝑈1 + 𝑈2 + ⋯ + 𝑈𝑁
Com relação a Lei de OHM temos que: 𝑈𝐴𝐵 = 𝑅𝑒𝑞 ∙ 𝑖.
Como todo resistor passa pelo processo de efeito Joule dissipando calor como
forma de energia e para isso é preciso calcular. Através da fórmula 𝑃 = 𝑈 ∙ 𝑖.
3.
OBJETIVO
Utilizando-se de instrumentos de medidas e software didático comprovar as leis
de Ohm, bem como determinar resistor equivalente, potência, corrente elétrica e
tensão em cada resitor. Determinar a tensão e corrente elétrica.
4.
MATERIAIS NECESSÁRIOS

1 resistor 1k;

1 resistor 0,5k;

1 resistor 0,9k;

1 fonte de 12V CC

1 multímetro completo com as pontas de provas;

2 cabos vermelhos com pino Jack e jacaré;

2 cabos pretos com pino Jack e jacaré;

1 placa protoboard;
5.
DIAGRAMA
Figura 1: Esquema montado no software Proteus 8.1
Conforme demonstra a Fig. 1 temos uma associação em série de resistores em
que, foi medido a corrente em cada resistor e sua diferença de potencial.
6.
PROCEDIMENTOS
a) Colocar três resistores em associado em séries fixado de modo correto no
Protoboard.
b) Medir com o multímetro a resistência de cada resistor.
c) Tomar nota de cada valor obtido na tabela 1
d) Fazer a leitura através das faixas de cores e anotar na tabela 1.
e) Medir o resistor equivalente utilizando-se do multímetro e anotar na tabela
1.
f)
Efetue a soma dos três resistores medidos no início do experimento.
g) Compare os resultados obtidos com o multímetro e o resultado somado.
Resistor
Valor Medido
Ω
Descrever a cor de cada faixa
1ª Faixa
2ª Faixa
3ª Faixa
Valor
4ª Faixa
1
2
3
Soma
Valor medido com o multímetro
Tabela1
7.
ATIVIDADES PROPOSTAS
1) Qual o valor do resistor equivalente?
2) Determinar o valor da tensão em cada resistor?
3) Quanto ao calor dissipado pelos resistores qual deles apresenta a maior
dissipação de calor por efeito Joule?
4) Será que realmente a corrente elétrica se apresenta constante em todo
circuito?
5) Monte uma relação entre a resistência Ohmica e o calor dissipado?
6) Se em vez de usar resistor, se tivessemos usados três lâmpadas, como seria
a relação entre o brilho e sua resitência?
8.
REFERENCIAS:
Walker, J.; Fundamentos de Física; Volume 3; 8ª Edição; Editora Livro Técnico
Científico; Rio de Janeiro; RJ; 2010.
https://williamevilasio.files.wordpress.com/2013/03/tabelas-de-resistores-mais-utilizados-naeletrc3b4nica.pdf acessado em 25/06/2015
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Danilo Capelari
Tema: Associação de Resistores em Paralelo
Assunto: Eletrodinâmica
1. INTRODUÇÃO
A Lei de Ohm, assim designada em homenagem ao seu formulador, o físico
alemão Georg Simon Ohm (1787-1854), afirma que, para um condutor mantido à
temperatura constante, a razão entre a tensão entre dois pontos e a corrente elétrica
é constante. Essa constante é denominada de resistência elétrica.
2. OBJETIVO

Reconhecer e montar uma associação de resistores em paralelo e determinar
o valor da resistência equivalente de uma associação em paralelo
comparando-o ao valor teórico.

Determinar, através de medidas, o valor da corrente elétrica que atravessa
cada um dos resistores e compara-la com o valor teórico calculado
anteriormente.
3. MATERIAL NECESSÁRIO
- 1 Multímetro
- Resistores: 1,2 kΩ; 3,9 kΩ; 4,7 kΩ
- Pontas de Prova
- 1 placa Protoboard
- 1 fonte de tensão
- Cabos de conexão
4. PROCEDIMENTOS
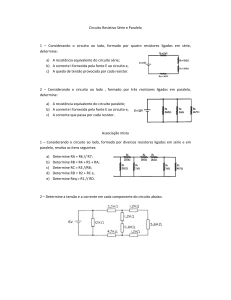
1 – Considere o circuito abaixo e calcule a resitência equivalente dos resistores.
Anote o valor encontrado na tabela 1.
Figura 1 – associação de resistores em paralelo
2 – Conecte o multímetro (conforme figura abaixo), devidamente ajustado para a
escala de Ohms aos ponto A e B, faça a leitura e anote o valor na tabela 1
Figura 2 – montagem
REq calculada
REq medida
Tabela 1 – resistência equivalente
3 – Compare o valor calculado com o valor medido (ohmímetro) e discuta o resultado.
4 – Conecte a fonte de tensão ao circuito da figura 2.
5 – Ligue e ajuste a fonte para 10V.
6 – Utilizando a escala correta, meça a voltagem em cada resistor. Anote abaixo:
________ - R1
________ - R2
________ - R3
7 – Meça a voltagem da associação em paralelo.
_________ - Associação
8 – Relacione os valores encontrados nos itens 6 e 7.
9 – Faça o cáculo da corrente elétrica que atravessa cada um dos resistores e anote
abaixo.
________ - R1
________ - R2
________ - R3
10 – Agora meça, na escala correta, a corrente que atravessa cada um dos resistores
e anote abaixo. Faça uma comparação entre o valor calculado e o valor medido e
discuta o resultado.
________ - R1
________ - R2
________ - R3
5. REFERÊNCIAS
RAMALHO; NICOLAU E TOLEDO. Os fundamentos da Física: Vol.3. 7a ed. São
Paulo: Moderna, 2001
FUSINATO, Polonia Altoé; BATISTA, Michel Corci. Eletricidade Básica – Caderno
de atividades experimentais. Ed. Massoni
MINISTÉRIO DA EDUCAÇÃO E CULTURA
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Elissandra Beneti Cateli Mangolin
Tema: Associação Mista de Resistores
Assunto: Eletrodinâmica
1. INTRODUÇÃO
Todos os corpos oferecem normalmente maior ou menor dificuldade à passagem
da corrente elétrica. A característica de um condutor que é relevante nesta situação é a
resistência (R).
Em 1826, George Simon Ohm descobriu que para condutores metálicos a tensão
varia linearmente com a corrente elétrica, ou seja, a razão entre a tensão e a corrente
elétrica é constante, e esta constante é denominada resistência R do condutor que é dada
pela equação:
𝑹=
𝑼
𝒊
Em que U é a diferença de potencial nas extremidades do condutor e i é a
intensidade da corrente elétrica que o atravessa. A unidade de resistência elétrica no SI é
dada pela razão Volt/Ampère e recebe o nome de ohm (Ω).
Ele também observou que mantida a temperatura constante, a tensão e a
intensidade da corrente são diretamente proporcionais.
𝑼𝟏 𝑼𝟐 𝑼 𝟑
=
=
= 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆
𝒊𝟏
𝒊𝟐
𝒊𝟑
E formulou a equação abaixo conhecida como a 1ª Lei de Ohm.
𝑼 = 𝑹 .𝒊
1.1 ASSOCIAÇÃO EM SÉRIE
Na associação em série todos os resistores são percorridos pela mesma corrente
elétrica. Os resistores são ligados um em seguida do outro, existindo apenas um caminho
para a corrente elétrica. Observe a figura abaixo:
Figura 1 – Associação em série
A ddp de uma associação de resistores em série é a soma das ddps em cada um
dos resistores associados.
O valor da resistência equivalente é dado pela soma das resistências dos resistores
que constituem a série.
1.2 ASSOCIAÇÃO EM PARALELO
A associação de resistores em paralelo é um conjunto de resistores ligados de
maneira a todos receberem a mesma diferença de potencial (ddp). Nesta associação
existem dois ou mais caminhos para a corrente elétrica, e desta maneira, os resistores não
são percorridos pela corrente elétrica total do circuito. Observe a figura.
Figura 2 – Associação em paralelo
A corrente, em uma associação de resistores em paralelo, é a soma das correntes
nos resistores associados.
Na associação em paralelo, o valor da resistência equivalente é sempre menor que
o valor de qualquer resistência dos resistores da associação. Este valor pode ser obtido
com as seguintes equações:
1.3 ASSOCIAÇÃO MISTA
Uma associação mista é composta quando associamos resistores em série e em
paralelo no mesmo circuito. Observe na figura abaixo que os resistores R1 e R2 estão em
série e os resistores R3 e R4 estão em paralelo:
Figura 3 – Associação mista
Nas associações mistas também podemos encontrar um valor para a resistência
equivalente. Para isto devemos considerar cada associação (série ou paralelo)
separadamente, sendo que todas as propriedades descritas acima são válidas para estas
associações.
2. OBJETIVO
Como já vimos, associação mista são aquelas em que encontramos, ao mesmo
tempo, resistores associados em série e em paralelo. A determinação do resistor
equivalente de cada uma das associações envolvidas.
Figura 3 – Circuito elétrico misto

Reconhecer, e montar uma associação mista de resistores;

Medir tensão e corrente em cada resistor;

Determinar o resistor equivalente de uma associação mista de resistores;
3. MATERIAIS NECESSÁRIOS

Multímetros;

Fonte de tensão: 15V;

Resistores de 1,5 kΩ; 1,8 kΩ ; 2,2 kΩ; 2,7 kΩ; e 3,3 kΩ;

Pontas de Prova;

Protoboard;

Cabos de conexão.
4. PROCEDIMENTOS
4.1. Monte o circuito representado abaixo no protoboard, na seguinte sequencia R1= 1,8
kΩ; R2= 2,2 kΩ; R3= 1,5kΩ; R4= 2,7 kΩ e R5= 3,3 kΩ
Figura 4 – Circuito misto esquematizado
4.2. Calcule o valor da resistência equivalente nos conjuntos ReqA (R1, R2) e ReqB (R4, R5),
resistência equivalente total REqTotal , anote na Tabela 1 e redesenhe o circuíto.
Resistores
REq Calculada
ReqA
ReqB
REqTotal
Tabela 1 – Resistência equivalente calculada (Ω)
4.3. Conecte o multímetro, devidamente ajustado para a escala de Ohms, aos pontos ReqA;
ReqB, e REqTotal faça a leitura e anote o valor na Tabela 2.
Resistores
REq Medida
ReqA
ReqB
REq Total
Tabela 2 – Resistência equivalente medida (Ω)
4.4. Calcule a tensão e a corrente em cada resistor R1, R2, R3, R4 e R5, faça a leitura da
medida com o multímetro e anote os valores na Tabela 3, para devidas comparações.
Obs: Para obtenção dos resultados, conecte o multímetro em série para a leitura da corrente
(A) e em paralelo para a leitura da tensão (V).
Resistor U medido
U calculado
I medido
R1
R2
R3
R4
R5
Tabela 3 – Tensão (U) e Corrente (I)
I calculado
4.5. Compare o valor dos resistores nominais com o valor medido no multímetro e discuta
o resultado em termos de tolerância.
Lembrando:
COR
Ouro
Prata
Sem cor
Resistor
TOLERÂNCIA
+/- 5%
+/- 10%
+/- 20%
Valor nominal kΩ
Valor medido kΩ
R1
R2
R3
R4
R5
Tabela 4 – Resistência Nominal (kΩ) e Medido (kΩ)
Obs:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
5. REFERÊNCIAS
BATISTA, Michel Corci; FUSINATO, Polônia Altoé; Eletricidade Básica, Caderno de
Atividades Experimentais, Editora Massoni; 1ª Edição, Maringá-PR, 2014.
GASPAR, Alberto; Compreendendo a Física, 2 Volume, Ensino Médio, Editora Ática,
1ª Edição, São Paulo, 2011, pg. 395.
SILVA,
Marco
Aurélio;
Associação
de
Resistores,
Disponível
em:
http://www.brasilescola.com/fisica/associacao-resistores.htm, Acesso em: 15 de abril
de 2015.
PR
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
UNIVERSIDADE TECNOLÓGICA FEDERA DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Jardel Santos Cipriano
Tema: Ponte de Wheatstone
Assunto: Eletrodinâmica
1. INTRODUÇÃO
A ponte de Wheatstone é um circuito eletrônico de vasta aplicação em
aparelhos de medição tais como: medidores de resistência, termômetros, etc.
Seu circuito básico é mostrado abaixo:
FIGURA 1 – Circuito básico de uma ponte de Wheatstone
Quando a ponte está em equilíbrio, obedecendo uma certa relação entre seus
resistores, a tensão na saída (VOUT) será igual a zero.
Para que isso ocorra devemos ter:
Daí podemos então deduzir como fica a relação entre esses resistores:
R2.R4 = R1.R3
Desta forma, para qualquer tensão de entrada, a tensão na saída será sempre zero,
desde que obedecidas as relações deduzidas acima. Nestas condições, dizemos que
a ponte está em equilíbrio.
Para desequilibrar a ponte, basta alterar o valor de qualquer um dos resistores.
A tensão VOUT então poderá assumir valores negativos ou positivos (supondo
o ponto D como referência).
2. OBJETIVO
a) Analisar os ramos da ponte de Wheatstone.
b) Determinar o valor aproximado da resistência não conhecida no circuito.
3. MATERIAIS NECESSÁRIOS

Fonte variável

Resistores: 100Ω, 150Ω

Potenciômetro

Multímetro

Protoboard
4. PROCEDIMENTOS
Iniciamos o experimento com a proposta de utilizar a ponte de Wheatstone para
identificar resistências desconhecida no sistema, utilizando um potenciômetro e a
equação
característica
da
mesma.
Uma
ponte
foi
montada
em
uma
protoboard contendo três resistores e um potenciômetro linear, sendo que um dos
resistores não tem o valor conhecido.
FIGURA 1 – A figura mostra a ponte montada com R3 desconhecido
Iniciamos o experimento ativando a fonte e verificando a tensão central com o
auxílio do multímetro em função voltímetro, sendo que o potenciômetro estava
ajustado de forma a exercer a menor resistência possível, o resultado obtido foi de
+0,76V.
FIGURA 2 – A figura mostra a leitura antes da ponte entar em equilibrio
O potenciômetro foi deslocado na direção horária levemente até que o valor
registrado no instrumento de medição atingisse 0V, ao alcançar este valor, a fonte foi
desativada e o potenciômetro foi removido do circuito e com o auxílio do multímetro
em função ohmímetro, aferiu-se o valor de 147,8Ω.
FIGURA 3 – A figura mostra a ponte em equilibrio, o multimetro acusa 0V.
Logo já é possível determinar o valor da resistência desconhecida, através da
fórmula:
R2.R3 = R1.Rv
R3= 98,53 Ω
4.3 ATIVIDADES PROPOSTAS
a) Recrie o experimento utilizando diferentes resistores e potenciômetro,
utilisados anteriormente.
5. REFERÊNCIAS
Capuano, F. G., & Marino, M. A. (2009). Laboratório de Eletricidade e Eletrônica (24ª
Edição ed.). Érica.
Gussow, M. (2009). Eletricidade Básica (2ª Edição ed.). (J. L. Nascimento, Trad.) Porto
Alegre: Bookman.
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluno: Silvio Marcos Pilatti
Tema: Circuito RC em série
Assunto: Eletrodinâmica
1. INTRODUÇÃO
1.1. CAPACITOR
Um capacitor é um dispositivo útil para armazenar carga elétrica e energia,
consistindo de dois condutores isolados um do outro entre os quais existe um
material isolante (dielétrico), como o ar, papéis, vidro, entre outros, que define o tipo
de capacitor.
Ligando-se um capacitor à uma fonte de tensão contínua, por exemplo uma
bateria, há transferência de carga de um condutor para o outro (através da bateria)
até que a ddp entre os dois condutores devido às cargas iguais e opostas seja igual
à ddp entre os terminais da fonte, nesse instante o capacitor estará carregado.
Existem vários tipos de capacitores, a figura abaixo mostra alguns exemplos.
Em um circuito, o capacitor geralmente é representado da forma mostrada na
figura abaixo:
A quantidade de carga separada, Q, depende da geometria do capacitor (por
exemplo, da área e da separação entre as placas no caso de um capacitor de placas
paralelas) e é diretamente proporcional à ddp aplicada, V. A constante de
proporcionalidade é chamada capacitância, C. Então:
C
Q
V
Onde:
C = Capacitância
Q = Carga Elétrica
V = Tensão
Quando aplicarmos uma tensão igual a 1 volt (V) e o capacitor armazenar 1
Coulomb (C), teremos então uma capacitância igual a 1 farad (F).
Devido às dificuldades construtivas, os capacitores encontram-se situados em
faixa de valores submúltiplos do farad como o micro farad (μ F), nano farad (nF) e o
pico farad (pF).
1 μ F = 10-6 F
1 nF = 10-9 F
1 pF = 10-12 F
A figura abaixo representa uma situação prática de carga e descarga de um
capacitor, usando uma bateria (neste caso duas pilhas) e um LED.
Abaixo temos a representação do fluxo de elétrons num processo de carga (a)
e descarga (b) de um capacitor.
1.2. Circuito RC em série
Se ligarmos em série um capacitor, um resistor e uma bateria, estamos
construindo o que chamamos circuito RC em série.
Quando um circuito é ligado, há um período de transição, durante o qual a
corrente e a queda de tensão variam de um valor inicial até um valor final em todos
os elementos. Depois deste período de transição, chamado transiente, o circuito é
dito estar em regime estacionário.
Analisemos agora o circuito transiente RC com tensão contínua aplicada,
conforme mostra a figura:
Tomemos a chave S na posição B. Nesta posição o capacitor estará
descarregado. Quando colocamos a chave na posição A, o capacitor começa a
carregar até atingir um valor máximo de carga, Qmáx = ε.C.
A tabela abaixo identifica as expressões matemáticas para carga e descarga
do capacitor.
O instante t = RC é denominado constante de tempo capacitiva do circuito, e
indicado pela letra τ . De acordo com a equação t = RC, uma constante de tempo é
igual ao tempo necessário para carregar um capacitor até 63% de sua tensão máxima.
Em geral, pode-se considerar um capacitor completamente carregado após decorrido
um tempo da ordem de cinco constantes de tempo (t = 5τ) pois neste caso V C = 99%
de V0.
Logo teremos:
1. Num instante inicial (chave S na posição A, figura 6): t = 0, temos V R = V0 e
VC = 0
2. Num instante intermediário: t = RC, temos VR = 0,37V0 e VC = 0,63V0
3. Ao fim do carregamento: t = ∞, temos VR = 0 e VC = V0
O gráfico abaixo mostra a variação da tensão no capacitor e no resistor em
função do tempo de carga do capacitor.
2. OBJETIVOS
a) Levantar, em um circuito RC, curvas de tensão no resistor e no capacitor em função
do tempo durante a carga do capacitor.
b) Levantar, no mesmo circuito RC, curvas de tensão no resistor e no capacitor em
função do tempo durante a descarga do capacitor.
c) Medir a constante de tempo de um circuito RC.
3. MATERIAIS NECESSÁRIOS
Materiais e componentes
•
1 Fonte de tensão 12V DC;
•
1 resistor 100kΩ x 1/8W (marrom, preto, laranja);
•
1 capacitor de 1000 μF/25V;
•
1 Cronômetro;
•
3 Conectores Jacaré;
•
2 Voltímetros;
•
4 Fios link;
•
1 Placa Protoboard.
4. PROCEDIMENTOS
4.1 CONSTANTE DE TEMPO- CARREGANDO O CAPACITOR
a) Faça a montagem do circuito da figura 6, utilizando o capacitor e o resistor
fornecidos;
b) Conecte um voltímetro em paralelo com o capacitor;
c) Conecte um voltímetro em paralelo com o resistor;
d) Cuidado !! O terminal (+) do capacitor é o borne vermelho.
e) Como o capacitor suporta no máximo 25V, utilize uma escala do voltímetro maior
que este valor.
f) Ligue a chave S no ponto A, ao mesmo tempo que o cronometro, anotando os
valores de tensão no resistor e no capacitor em intervalos de tempo de 10 segundos,
usando a tabela abaixo:
g) Faça o diagrama tensão versus tempo (V x t) para o capacitor e para o resistor.
h) Qual o valor da constante de tempo? Compare o valor experimental com o valor
calculado τ = RC.
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
i) Qual é a relação entre a constante τ e o tempo de carga do capacitor?
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
4.2. CONSTANTE DE TEMPO – DESCARREGANDO O CAPACITOR
O procedimento é análogo ao anterior, exceto pelo fato de que o capacitor é
descarregado por meio do resistor.
a) Ligue a chave S no ponto B gerando um curto circuito.
b) Anote, na tabela abaixo, o valor das tensões no resistor e no capacitor, em
intervalos de tempo de 10 segundos:
c) Faça o diagrama tensão versus tempo (V x t) para o capacitor e para o resistor, no
processo de descarga:
d) Faça um diagrama tensão versus tempo (V x t) para o capacitor no processo de
carga e descarga.
5. REFERÊNCIAS
HALLIDAY, D., RESNICK, R. Fundamentos de Física, 3.ed,Rio de Janeiro: Livros
Técnicos e Científicos Editôra S.A, 1993. v.3, p. 125 _ 129.
TIPLER, P. A. Física, 2.ed, Rio de Janeiro: Guanabara Dois, 1984. v.2a, p. 714 - 717.
Roteiros para Laboratório _ Eletricidade e Magnetismo, IFUFRGS,www.if.ufrgs.br/fis01202/index_lab.html, página acessada em 11/05/2015.
Zaro, M., Borchardt I. e Moraes J.: Experimentos de Física Básica - eletricidade,
magnetismo, eletromagnetismo - 1982.
CREDER, H. Instalações Elétricas. Rio de Janeiro, Livros Técnicos e Científicos,
Editora S.A., 1974.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Geislana Padeti Ferreira Duminelli
Tema: Circuito simples de controle de brilho de um LED com potenciômetro
Assunto: Eletrostática
1. INTRODUÇÃO
Um potenciômetro é um componente eletrônico que possui resistência
elétrica ajustável. Geralmente, é um resistor de três terminais onde a conexão central
é deslizante e manipulável. Se todos os três terminais são usados, ele atua como
um divisor de tensão.
Existem comercialmente, potenciômetros confeccionados com substrato em fio
e carvão condutivo, a depender da corrente elétrica que circula nestes. Há
potenciômetros cujo giro é de 270 graus e outros de maior precisão chamados multivoltas.
Em relação à curva de resposta em função do ângulo de giro do eixo, existem
dois tipos de potenciómetros, os lineares (sufixo B ao final do código) e os logarítmicos
(sufixo A ao final do código comercial do valor).
Exemplo de especificação de potenciômetro linear: 50 KΩ, ou seja, de 50.000 ohms,
linear.
Os potenciômetros lineares possuem curva de variação de resistência
constante (linear) em relação ao ângulo de giro do eixo. Os potenciômetros
logarítmicos, por sua vez, apresentam uma variação de resistência ao ângulo de giro
do eixo mais adaptada à curva de resposta de audibilidade do ouvido humano.
Considerando um aparelho de som, os potenciômetros lineares são recomendados
para uso em controle de tonalidade (graves, médios e agudos) já os logarítmicos são
mais recomendados para controles de volume.
2. OBJETIVO
 Montagem de um circuito utilizando o potenciômetro para controle de brilho
de um LED. O potenciômetro é um componente eletrônico de resistência variável
geralmente utilizado para ajustar parâmetros, como o volume de aparelhos de
som, brilho e contraste de telas LCD. Mas pode ser utilizado como um sensor de
posição em robôs e equipamentos industriais, onde são destinados a informar a
angulação exata de um braço mecânico, ver figura 1, os símbolos dos
componentes eletrônicos a serem utilizados.
3. MATERIAIS NECESSÁRIOS
 1 Multímetro
 Pontas de prova
 Cabos de conexão
 1 LED
 1 Potenciômetro de três terminais: 100 kΩ
 1 Resistor: 350 Ω.
 1 Protoboard
 Fonte de tensão
Figura 1: Símbolos dos componentes eletrônicos
Antes da prática, verificar o comportamento da resistência do potenciômetro com o
ohmímetro.
4. PROCEDIMENTOS
a) Conecte o LED, o potenciômetro, o resistor de modo a criar uma ponte entre o
positivo, ânodo, do LED e uma das extremidades do potenciômetro e a fonte variável,
conforme a figura 2.
Figura 2: Circuito elétrico simples com diodo, resistor e potenciômetro
Cálculo de um resistor mínimo para que o LED não venha queimar, na condição do
potenciômetro em 0 Ohm ou na resistência mínima.
Resistência = (Tensão da Fonte – Tensão do LED)/Corrente suportada pelo LED
Este experimento seguirá uma sugestão de uso, podendo ser utilizado um LED de luz
branca de 2 V e 30 mA, com invólucro vermelho e uma fonte de 12 Volts. Assim:
Resistência = (12 - 2)/0,03 A = 333,3 Ohms, conforme a figura 3, poderá calcular o
valor da resistência do resistor fixo, utilizando o código de cores.
Figura 3: tabela de código de cores para resistores
Resistor Ideal 1ª – Faixa: Laranja (3)
2ª – Faixa: Verde (5)
3º - Faixa [multiplicador]: Marrom (x10)
A partir da fórmula, calculou-se que o ideal seria um resistor de 350 Ohms da cor laranja
– verde – marrom, contudo é comum não se ter o resistor ideal em mãos, por isso procure por
valores aproximados, SEMPRE PARA MAIS!
b)
Adicione os fios conectores, um entre o negativo, cátodo, do LED e o negativo,
cátodo, da fonte. O outro entre o positivo, anodo, da fonte e o pino central do potenciômetro.
Cuidado ao conectar os fios, verifique se estão formando as ligações corretas, conforme a
figura 4.
Figura 4: Representação esquemática da montagem do circuito
4.1 ATIVIDADES PROPOSTAS
1. Calcule o valor da intensidade da corrente elétrica teoricamente nas condições em
que o potenciômetro estiver na mínima e máxima resistência, fazendo uma
analogia com o brilho do Led.
2. Agora, de acordo com o exercício 01, faça a comprovação dos resultados
utilizando o multímetro e medindo em seu circuito.
3. Comprove pela Lei de Kirchhoff das tensões, a medida de tensão em cada
componente teoricamente e na prática, em seguida faça a soma.
Tabela 1 – Medida de tensão de cada componente (Volts)
Tensão (V) Teórico
Tensão (V) Prático
Led
Potenciômetro
Resistor
5. CONSIDERAÇÕES FINAIS
A montagem do circuito proporciona ao estudante, um aprendizado satisfatório, pois a
partir do momento em que o LED ascende, se torna imprescindível verificar que ao girar o
botão do potenciômetro será possível perceber a alteração de intensidade luminosa. Isso
ocorre porque, o potenciômetro é um componente eletrônico, assim como o resistor, capaz de
restringir a passagem de corrente elétrica, contudo a resistência do potenciômetro é ajustável,
variando de 0 Ohms a resistência máxima do componente. Quando se aumenta a resistência
do potenciômetro, a corrente chega com menor intensidade ao LED, e quando se diminui a
resistência, a corrente chega ao LED com maior intensidade, aumentando a luminosidade.
6. REFERENCIAS
BATISTA, Michel Corci; FUSINATO, Polônia Altoé; Eletricidade Básica, Caderno de
Atividades Experimentais, Editora Massoni; 1ª Edição, Maringá-PR, 2014.
https://sites.google.com/site/netaula/blog/circuitosimplesdecontroledebrilhodeumledc
ompotenciometro, visitado em 13 de abril de 2015 as 09:25.
https://www.youtube.com/watch?v=HGi0ofysniw, visitado em 13 de abril de 2015 as
09:31.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Joslaine de Lima
Tema: Transformadores
Assunto: Eletrodinâmica
1. INTRODUÇÃO
Transformadores são dispositivos que transformam tensão ou corrente elétrica
em níveis de grandeza diferentes, para aplicações específicas. Em princípio não há
uma transformação de energia, apenas mudanças nos valores de tensão e/ou
corrente, porém há perdas, e a energia resultante torna-se menor que a energia
inicial.
Um transformador é composto de, no mínimo, uma bobina primária e outra bobina
secundária. Quando alimentamos a bobina primária com uma tensão elétrica, esta
gera um campo magnético que irá interferir na bobina secundária, induzindo uma
corrente elétrica nesta, ocasionado o surgimento de uma tensão elétrica na bobina
do secundário como indicado na figura 1.
Figura 1 – Indução da Corrente elétrica
Porém, para haver corrente induzida, é necessário que a espira do
secundário corte linhas de força diferentes. Como o transformador não é móvel,
é necessário que o campo magnético seja variável, portanto, um transformador só
funciona com corrente alternada.
Sabemos que o campo magnético de uma bobina é diretamente proporcional
à tensão aplicada e ao número de espiras que a compõe. Assim também uma
bobina que está sendo induzida terá sua corrente induzida diretamente proporcional
ao campo magnético ao qual está exposta e ao número de espiras que a compõe.
Daí surge a seguinte expressão:
Isto resulta na relação de transformação: se um transformador é composto de
600 espiras no primário e 60 espiras no secundário, terá uma relação de 10:1
(redutor). Isto quer dizer que a tensão injetada no primário será reduzida em 10
vezes no secundário.
Sabemos que o transformador não transforma energia, portanto, a potência
elétrica do primário, desprezando as perdas, será igual à potência do secundário.
PPRIMÁRIO  PSECUNDÁRIO
Em termos de tensão e corrente,
isto quer dizer:
V PRIMÁRIO.I PRIMÁRIO  VSECUNDÁRIO.I SECUNDÁRIO
Quanto à forma de onda, acontece uma inversão do sinal do primário, devido
à transmissão por campo magnético (defasagem 90° corrente e campo) como
mostrada na figura 2.
Figura 2 - Relação de fase entre as
bobinas de um transformador
2. OBJETIVO
Compreender o funcionamento de um transformador e aprender a medir sua
resistência e tensão.
3. MATERIAIS NECESSÁRIOS:

1 transformador com saída 9V+9V

1 multímetro
4. PROCEDIMENTOS
TESTE DO TRANSFORMADOR A FRIO – medida de sua resistência.
4.1.
a) Inicialmente coloca-se o multímetro na escala de resistência (fundo de escala
200Ω).
b) Em seguida meça a resistência entre o fio preto e o fio azul e anote na
tabela 1.
c) Agora meça a resistência entre o fio azul e o fio vermelho e anote na tabela
1.
Rpreto - azul
Razul Vermelho
Tabela 1: valor da resistência medida no primário do
transformador
Porque você fez essa medida?
Este tipo de transformador possui um único primário para 220 V. Ligando um
fio extremo com o central do primário, ele funciona em 127 V. Caso o transformador
que você deseja utilizar esteja sem identificação a ligação em 127V deve ser feita
do central para o extremo de menor resistência
4.2.
MEDIÇÃO DE TENSÃO NO SECUNDÁRIO DO TRANSFORMADOR
a) Inicialmente coloque a chave seletora do multímetro na escala de tensão
alternada (20V~);
b) Monte o circuito da figura abaixo;
CUIDADO PARA NÃO TOMAR UM CHOQUE E NEM FECHAR UM CURTO
CIRCUITO ENTRE OS FIO!
c) Faça a medida da tensão entre o fio preto (central do secundário) e uma
extremidade e anote o valor na tabela 2.
d) Faça a medida da tensão entre o fio preto (central do secundário) e a outra
extremidade e anote o valor na tabela 2.
e) Faça a medida da tensão entre as duas extremidades e anote o valor na
tabela 2.
Tensão medida (Vrms)
Fio central e
extremidade 1
Fio central e
extremidade 2
Extremidade 1 e
extremidade 2
Tabela 2: valor da tensão medida no secundário do transformador
f) Preencha a tabela 3.
Tensão medida (Vrms)
Tensão calculada (Vp)
Fio central e
extremidade 1
Fio central e
extremidade 2
Extremidade 1 e
extremidade 2
Tabela 3: valor da tensão calculada no secundário do transformador
5. REFERÊNCIAS
GOUVEA. L. Transformadores monofásicos. 2010. Disponível em:
<http://www.ebah.com.br/content/ABAAAe5CcAG/transformadores-monofasicos>.
Acesso em 20 de abr. 2015.
BATISTA, M.C., FUSINATO, P.A., Eletricidade Básica: caderno de atividades
experimentais; Maringá: Massoni, 2014.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Elissandra Beneti Cateli Mangolin
Tema: Mini-motor elétrico
Assunto: Eletrodinâmica
1. INTRODUÇÃO
A força magnética é resultado da interação entre dois corpos dotados de
propriedades magnéticas, como ímãs ou cargas elétricas em movimento.
A força magnética, ou força de Lorentz, é resultado da interação entre dois
corpos dotados de propriedades magnéticas, como ímãs ou cargas elétricas em
movimento.
No caso das cargas elétricas, a força magnética passa a existir quando
uma partícula eletricamente carregada movimenta-se em uma região onde atua
um campo magnético.
Considerando que uma carga pontual Q, com velocidade v, é lançada em uma
região onde existe um campo magnético uniforme B, passa a atuar sobre ela uma
força magnética com intensidade dada pela seguinte equação:
F = Q.v.B.senα
*α é o ângulo entre os vetores da velocidade v e do campo magnético B.
A direção do campo magnético é perpendicular ao plano que contém os
vetores v e B, e o sentido é dado pela regra da mão direita. Observe a figura:
FIGURA 1 – A regra da mão direita mostra o sentido da velocidade, do campo e da força magnética
Fonte: http://www.brasilescola.com/fisica/forca-magnetica.htm
Veja que o dedo médio aponta na direção da velocidade v em que a carga
está movimentando-se, já o indicador indica a direção do campo magnético B. O
polegar aponta no sentido da Força magnética F.
O movimento adquirido pela carga elétrica ao entrar em contato com o campo
magnético depende do ângulo em que ela foi lançada.
A unidade de medida da força magnética é a mesma de qualquer outro tipo
de força: o Newton. Existem inúmeras aplicações da força magnética, dentre elas,
podemos citar os motores elétricos.
2. OBJETIVO

O experimento objetiva levar o aluno a ter um contato maior com os motores
elétricos, bem como ajudá-lo a entender o princípio de funcionamento desses
motores.

É um experimento de baixo custo que visa à interação dos alunos com o
estudo da física aplicada no dia a dia.

Você aprenderá a montar um motor elétrico básico (realmente básico), com
uma rotação de até 10.000 rpm, em apenas 30 segundos!

Trata-se montar uma composição com elementos simples que atuam com
base nos princípios de funcionamento de um motor elétrico.
3. MATERIAIS NECESSÁRIOS

Um parafuso simples de rosca soberba (usado em madeira de cabeça chata);

Uma pilha alcalina tamanho grande (1,5 V);

Um fio de cobre (condutor) de aproximadamente 8 polegadas (20 cm), com as
pontas descascadas;

Um imã de neodímio de 22 mm x 10 mm (pode ser outro, porém circular);

Uma base de metal que seja atraído pelo ímã de neodímio, que lembre uma
hélice (pode ser a tampa de uma extrato de tomate);
FIGURA 2 – Materiais utilizados: Parafuso (cabeça chata), hélice de tampa de extrato de tomate,
pilha 1,5V, fio de cobre e o ímã de neodímio
4. PROCEDIMENTOS
4.1 Junte o ímã de neodímio com a base do parafuso de um lado e do outro junte a
base de metal em forma de hélice (fig. 3);
FIGURA 3 – Primeira parte do procedimento
4.2 Feito isso, coloque a ponta do parafuso no polo positivo da pilha, pressionando
uma extremidade do fio de cobre no seu lado oposto (polo negativo), (fig. 4);
FIGURA 4 – Mini motor montado
Pronto, seu motor está finalizado.
Para “dar ignição”, basta tocar o ímã de neodímio com a outra ponta do fio de cobre.
O parafuso passará a executar voltas o suficiente para estampar um sorriso em seu
rosto.
4.3 ATIVIDADES PROPOSTAS
a) Como podemos vaiar a velocidade do giro do parafuso?
b) O que acontecerá se o parafuso ficar do lado negativo da pilha? Justifique?
c) O que acontecerá se ímã for invertido, inverter os lados do parafuso com a
hélice? Justifique.
d) Qual o sentido da força magnética, velocidade e campo através da regra da
mão direita, para os itens 2 e 3.
5. REFERÊNCIAS
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de Física:
Eletromagnetismo, Volume 3; LTC; 2012.
KAZUHITO, Yamamoto; FUKE, Luiz Felipe; Física para o Ensino Médio:
Eletricidade Física Moderna, Volume 3, Saraiva, pg.219, 2013.
MENDES,
Marieane;
Força
Magnética.
Disponível
em:
http://www.brasilescola.com/fisica/forca-magnetica.htm. Acesso em 29 de junho de
2015.
MINISTÉRIO DA EDUCAÇÃO E CULTURA
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
CAMPUS CAMPO MOURÃO
Mestrado Nacional Profissional em Ensino de Física
Disciplina: Atividades Experimentais para o Ensino Fundamental e Médio
Aluna: Washington Roberto Lerias
Tema: Motor Elétrico Caseiro Didático
Assunto: Eletrodinâmica
1. INTRODUÇÃO
É fascinante o fato de poder dominar alguma tecnologia, aplicando e confirmando os
conhecimentos teóricos na prática. A montagem do motor elétrico e as atividades propostas
neste experimento são direcionadas à última aula de eletromagnetismo do 3º ano do ensino
médio.
2. OBJETIVOS
Este experimento tem como objetivo, explorar conteúdos do eletromagnetismo,
utilizando materiais de baixo custo, na construção de um motor elétrico caseiro e seus
princípios de funcionamento.
3. MATERIAIS
Fig.1 - Materiais utilizados
 1 pilha grande 1,5V
 1 ímã de auto falante
 60cm de fio sólido fino esmaltado desencapado; Sugestão de 19-21 awg
 30cm de fio sólido grosso; Sugestão de 1,5-2,5 mm
 1 ferro de solda
 estanho
 pasta de solda
 lixa
 alicate de bico
 alicate de corte
 régua ou trena
 multímetro
4. PROCEDIMENTOS
4.1. MONTAGEM
 Cortar o fio grosso em duas partes iguais de 10 a 15 cm;
Fig.2 - Fio que servirá de mancal
 Descascar e lixar bem as duas extremidades;
 Fazer um gancho com a abertura para cima em uma das extremidades de
ambas as partes, conforme figura, que servirá de suporte (mancal) para os
eixos da espira;
Fig.3 - Modelo de mancal
 Soldar a outra extremidade das partes na pilha, uma no lado positivo e a outra
no seu lado negativo, de forma que as partes fiquem paralelas entre si;
Fig.4 - Mancal soldado na pilha
 Com o auxílio de algum cilindro com cerca de 3 cm a 4cm de diâmetro, dar 5
voltas com o fio mais fino, cuidando que sobre uns 5 cm de cada lado e
centralizado conforme a figura, que servirá de eixo de rotação;
Fig.5 - Espira circular
 Lixar as extremidades dos eixos que estarão em contato com o suporte
(mancal), conforme esquema abaixo:
Fig. 6 - Esquema para confecção da espira de forma a simular corrente alternada
 Coloque os eixos da espira nos ganchos dos suportes da pilha;
 Aproxime o ímã direcionado à espira e a espira girará segundo o princípio de
funcionamento de um motor elétrico.
4.2. PROCEDIMENTOS TEÓRICO-METODOLÓGICOS
 Medir a resistência (R)da espira com o ohmímetro;
R = ___________Ω(ohm)
 Medir a diferença de potencial (U) da pilha com o voltímetro;
U = ___________V(volt)
 Utilizando a Lei de Ohm, U=Ri, calcular a corrente elétrica (i) estimada que
passa pela espira;
i = ____________A(ampère)
 Medir a corrente elétrica e compará-la com a estimada;
i = ____________A(ampère)
 Calcular o campo magnético ou o módulo do vetor indução magnética (B)
produzido pela corrente elétrica que atravessa a espira circular, sabendo que:
onde B no SI equivale ao A/m = T(tesla), n = nº de espiras,
µ0=4π.10-7 Tm/A = permeabilidade magnética no vácuo
espiras
e
= diâmetro das
B5 = ___________ T(tesla)
 Utilizando a Regra da Mão Direita, discutir a direção e o formato do campo
magnético;
Fig.8 - Regra da mão direita para uma espira circular
 Calcular a Força Magnética (FM) utilizando a expressão:
onde l=comprimento do fio e
= ângulo entre as direções do campo
magnético e a corrente elétrica
FM = _____________N
 Utilizando a regra da mão esquerda, identificar as direções do Campo
Magnético, Corrente Elétrica e a Força magnética.
Fig.9 - Regra da mão esquerda
 Calcular a potência elétrica (Pot ) do motor, utilizando-se da equação: Pot = iU
Pot = _____________W
 Calcular a energia elétrica Eel que o motor consumirá em kWh se ele
permanecer ligado por 48h:
Eel = P.Δt
Eel = _____________kWh
4.3. QUESTÕES E PROPOSTA DE ATIVIDADES
1) Como você faria para achar a frequência de rotação deste motor?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
2) Que dispositivo você colocaria no motor para ajudar a impulsionar o início da
rotação, ou seja, vencer a inércia?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
3) Como você faria para solucionar o problema do atrito entre o eixo e a base
(mancal)?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
4) Quais são as vantagens e desvantagens de se fazer muitas espiras neste
experimento?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
5) Quais as maiores dificuldades que você enfrentou para realizar este experimento?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
6) O que acontecerá se a espira se esquentar demais?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
7) Projete e construa o seu próprio protótipo de motor elétrico, buscando aperfeiçoar
e solucionar as dificuldades encontradas na sua construção e funcionamento:
5. REFERÊNCIAS
ALEXANDER, C.K.; SADIKU, M.N.O. Motores Elétricos e Acionamentos: Série
Tekne. 2013.
HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física 3,
Eletromagnetismo, Saraiva, 2012, 9ª Edição.