Exercícios de Análise de Circuitos com Kirchoff

Exercícios de Análise de Circuitos com Kirchoff – GVensino – http://gvensino.com.br
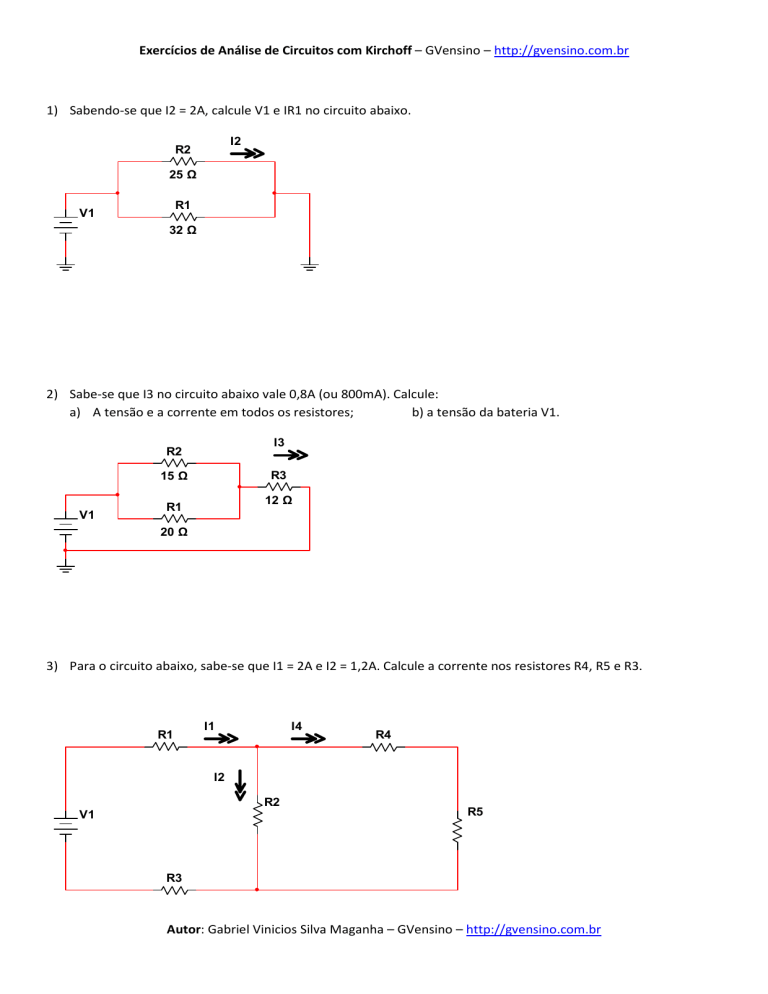
1) Sabendo-se que I2 = 2A, calcule V1 e IR1 no circuito abaixo.
I2
R2
25 Ω
R1
V1
32 Ω
2) Sabe-se que I3 no circuito abaixo vale 0,8A (ou 800mA). Calcule:
a) A tensão e a corrente em todos os resistores;
b) a tensão da bateria V1.
I3
R2
V1
15 Ω
R3
R1
12 Ω
20 Ω
3) Para o circuito abaixo, sabe-se que I1 = 2A e I2 = 1,2A. Calcule a corrente nos resistores R4, R5 e R3.
R1
I1
I4
R4
I2
R2
V1
R5
R3
Autor: Gabriel Vinicios Silva Maganha – GVensino – http://gvensino.com.br
4) Analise as tensões do circuito abaixo e calcule as tensões desconhecidas, sabendo-se que a bateria V1 possuí
uma tensão elétrica de 25V. Utilize a Segunda Lei de Kirchoff, lei das malhas.
6V
R1
R4
R5
R2
V1
R7
3V
3V
15 V
R8
R6
6V
1V
R3
R9
5) Analise o circuito abaixo, sendo R5 uma lâmpada que está dissipando uma potência 6W. Com as informações
que você tem no circuito, calcule a Tensão da Bateria V1:
R1
12 Ω
V1
R3
15 Ω
R2
R4
10 Ω
20 Ω
R5
VR5 = 12 V
PR5 = 6 W
Autor: Gabriel Vinicios Silva Maganha – GVensino – http://gvensino.com.br
Respostas:
1) Como I2 = 2A e R2 = 25 Ω, logo, VR2 = 50V. Como VR2 está em paralelo com a bateria e com VR1, logo, V1
também será 50V e VR1 = 50V.
Se VR1 = 50V e R1 = 32 Ω, IR1 será 50/32 => IR1 = 1,563A.
2) Se I3 = 0,8A e R3 = 12 Ω, logo, VR3 = 9,6 V.
Agora, vamos simplificar o circuito, resolvendo R1 e R2 em paralelo e desenhando o novo circuito. Ficaria:
I3
RA
RA =
15x 20
300
⇒ RA =
⇒ RA = 8,57Ω
15 + 20
35
8.57 Ω
R3
12 Ω
V1
Agora ficou um circuito em série. Portanto, IRA = IR3 (a corrente é a mesma). Portanto, IRA = 0,8A.
Podemos calcular VRA também: VRA = 8,57 x 0,8 -> VRA = 6,856V.
Portanto, temos:
6,856 V
9,6 V
RA
R3
8.57 Ω
12 Ω
V1
Letra a) Como R1 e R2 = RA, e R1 e R2 estão em paralelo, logo, a tensão de R1 e R2 será a mesma de RA. Portanto:
VR1 = 6,856V e VR2 = 6,856V
Portanto, IR1 = 6,856 / 20 -> IR1 = 343mA
IR2 = 6,856 / 15 -> IR2 = 457 mA
Letra b) Aplicando a segunda lei de kirchoff para o circuito série acima, sabemos que:
+VRA + VR3 – V1 = 0
+6,856 + 9,6 – V1 = 0
+16,456 – V1 = 0
Autor: Gabriel Vinicios Silva Maganha – GVensino – http://gvensino.com.br
16,456 = V1
Logo, V1 = 16,456 V
3) Aplicando-se a primeira Lei de Kirchoff (lei dos nós), sabemos que a soma das correntes que entram em
um nó é igual à soma das correntes que saem. Portanto, para o circuito dado, temos a seguinte
equação:
I1 = I2 + I4
2A = 1,2A + I4
2A – 1,2A = I4
0,8A = I4
Logo, IR4 e IR5 = 0,8A
IR3 = I2 + I4, pela 1ª lei de Kirchoff. Logo:
IR3 = 1,2A + 0,8A
IR3 = 2A
4) VR1 = 4V, VR6 = 6V, VR8 = 5V
5) Podemos calcular a corrente sobre a carga R5, através da fórmula IR5 = 6 / 12 -> IR5 = 0,5 A ou 500 mA.
Como R5 está em série com a bateria, sabemos que It = IR5. Portanto, It = 500 mA.
Para sabermos Vt, precisamos, além de It, sabermos o Rt. Então, vamos calcular a Req.
Pra calcular a Req, precisamos saber o valor de todos os resistores. Ainda não conhecemos o valor de R5, mas
podemos calcular este valor. Vejamos:
O resistor R5 possui uma resistência de: R5 = V2/P -> R5 = 144 / 6 -> R5 = 24 Ω
A REQ será igual a: R1 + [(R3 +R4) // R2 ] + R5 -> O símbolo // indica a associação paralela.
Portanto, a Req do circuito será de 43,777Ω
Logo, Vt = 46,777 x 0,5 -> Vt = 21,889 V
Observação: Esta não é a única maneira de resolver este exercício. Existem outras formas, mas todas levarão você
ao mesmo resultado.
Autor: Gabriel Vinicios Silva Maganha – GVensino – http://gvensino.com.br