Problema (flexão em 4 pontos)

Problema (flexão em 4 pontos)
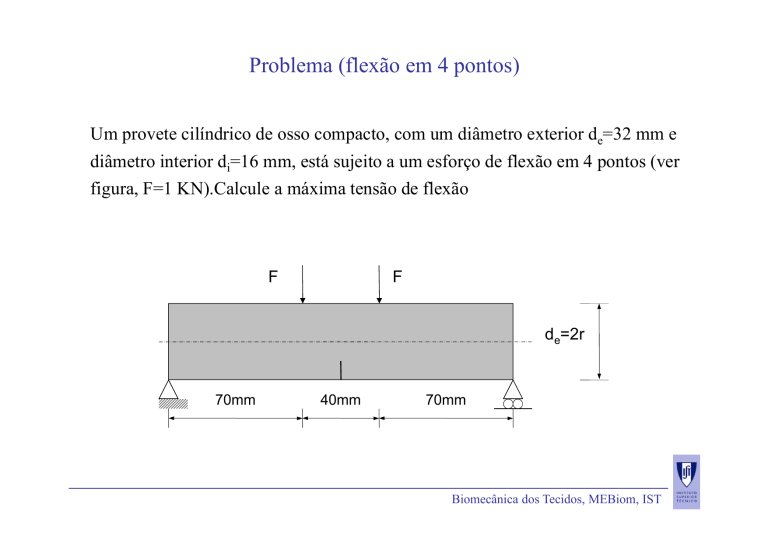
Um provete cilíndrico de osso compacto, com um diâmetro exterior de=32 mm e
diâmetro interior di=16 mm, está sujeito a um esforço de flexão em 4 pontos (ver
figura, F=1 KN).Calcule a máxima tensão de flexão
F
F
de=2r
70mm
40mm
70mm
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Problema (tensões principais)
Considere o estado de tensão bidimensional (estado de tensão plana):
6 3 
   

3
2



Determine as tensões principais e as correspondentes direcções principais.
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Problema (transformação de coordenadas)
Considere o estado de tensão bidimensional (estado de tensão plana):
6 3 
   

3
2



Escreva o anterior estado de tensão num referencial rodado de :
a) 90º
b) 18,4º
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Problema (transformação de coordenadas)
Considere o estado de tensão bidimensional (estado de tensão plana):
6 3 
   

3
2



Represente-o no circulo de Mohr.
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Tensão octaedral
z
y
x
 xx  xy  xz 

 yy  yz 


 zz 

3
1
 1 0 0 

2 0 
2 

 3 

Plano octaedral
1
3
1
3
 oct  ( 1   2   3 )  ( xx   yy   zz )
 oct
1
1
2
2
2 1/ 2
 ( 1   2 )  ( 2   3 )  ( 3   1 )   ( 2 I12  6 I 2 )1/ 2
3
3
1/ 2
1
 ( xx   yy ) 2  ( yy   zz ) 2  ( zz   xx ) 2  6( xy2   yz2   zx2 )
3
Biomecânica dos Tecidos, MEBiom, IST
Densidade de energia elástica de deformação
U 0    ij d ij
Para materiais lineares elásticos e isotrópicos, sujeitos a um estado de
tensão generalizado
1
U 0   ij  ij
2
U0 
1 2
1 2


 xx   yy2   zz2  2 ( xx yy   yy zz   zz xx ) 
 xy   yz2   zx2 
2E
2G
Quando apenas existe uma tensão xx
 xx2
1
U 0   xx xx 
2
2E
Biomecânica dos Tecidos, MEBiom, IST
Energia elástica de distorção
1
3
Tensão normal média
 a  ( 1   2   3 )   oct
Tensão desviadora
S      I 
ij
ij
 S xx



a
S xz   xx   a
 xy
 xz 
S yz   
 yy   a
 yz 
 

S zz  
 zz   a 
S xy
S yy
Ou seja, um estado de tensão pode ser decomposto na soma duma tensão
média com uma tensão desviadora
    I   S 
ij
a
ij
A componente média é responsável pela variação de volume
A componente desviadora é responsável pela alteração da forma
Biomecânica dos Tecidos, MEBiom, IST
Energia elástica de distorção
A energia elástica de distorção pode ser escrita na forma
U 0d 
1
3 2

 oct
( xx   yy ) 2  ( yy   zz ) 2  ( zz   xx ) 2  6( xy2   yz2   zx2 ) 
12G
4G
Alternativamente a energia elástica de distorção pode escrever-se em função
duma tensão equivalente (ou tensão de Von Mises)
U 0d 
onde
1 2
e
6G
1/ 2
1
2
2
2
2
2
2
( xx   yy )  ( yy   zz )  ( zz   xx )  6( xy   yz   xz )
e 
2
Num caso de tensão uniaxial, e=xx
Num caso de tensão hidroestático, e=0
Biomecânica dos Tecidos, MEBiom, IST
Critério de Von Mises
A entrada em cedência (em plasticidade) dum material isotrópico dúctil,
ocorre quando a energia elástica de distorção excede um valor limite
U 0d
 1  cedência
U 0d Y
Tendo em atenção a definição de tensão equivalente e que num ensaio
uniaxial, e=xx
U 0d
U 0d Y
1 2
 e   2
 6G
 e
1 2  Y 
Y
6G
Pelo que o critério de Von Mises pode ser escrito na forma
e
 1  cedência
Y
Biomecânica dos Tecidos, MEBiom, IST
Problema (critério de Von Mises)
Um provete cilíndrico, com um diâmetro exterior de=32 mm e diâmetro interior
di=16 mm, está sujeito a um momento flector M=140 N.m e a um momento
torsor T=210 N.m.
O material, considerado isotrópico, tem uma tensão de cedência e=115 MPa.
Verifique se existem condições para o material entrar em cedência.
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Problema (critério de Mohr)
Um provete cilíndrico, com um diâmetro exterior de=32 mm e diâmetro interior
di=16 mm, está sujeito a um momento flector M=140 N.m e a um momento
torsor T=210 N.m.
O material, considerado isotrópico, tem tendência a uma rotura frágil com
valores de tensão de falha à tracção tf=133 MPa e tensão de falha à compressão
cf=195 MPa.
Verifique se existem condições para a falha do material.
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST
Biomecânica dos Tecidos, MEBiom, IST