Gabarito

0.1 Problemas correspondentes ao Capítulo 2
1
0.1 Problemas correspondentes ao Capítulo 2
Cinemática unidimensional
1. A conclusão de Zeca está errada. Podemos verificar isso mesmo antes de fazer qualquer
cálculo, utilizando apenas a idéia de velocidade media. Como Juca percorreu distâncias
iguais com velocidades médias diferentes, os intervalos de tempo gastos para percorrer
cada trecho de 10km não são iguais. Gastou menos tempo no trecho em que manteve a
maior velocidade média. Conseqüentemente, sua velocidade média no trecho total não
pode ser, simplesmente, a média aritmética das respectivas velocidades médias em cada
trecho. Vejamos, agora, qual foi sua velocidade média em todo o movimento.
No trecho percorrido com a velocidade média de 12km/h, o tempo gasto por Juca foi
∆t1 = (10/12)h e no trecho percorrido com a velocidade média de 8km/h, o tempo gasto
foi ∆t2 = (10/8)h. Portanto, da definição de velocidade média, temos
hvi =
∆s
20
∆s
=
h
=
∆t
∆t1 + ∆t2
10/12 + 10/8
=⇒
hvi = 9, 6km/h .
(0.1)
Como era de se esperar, a velocidade média de Juca é menor que a média aritmética de
suas velocidades médias em cada trecho, uma vez que se movimentou mais tempo com a
velocidade média menor de 8km/h.
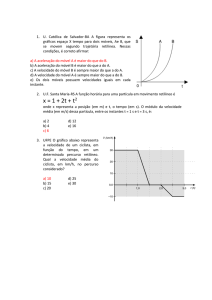
2.
(a) A partir das definições de velocidade e aceleração de uma partícula e sabendo que a
sua posição é dada por x(t) = −t2 + 6t + 16, obtemos
dx
= −2t + 6 ,
dt
dvx
=
= −2 .
dt
vx =
(0.2)
ax
(0.3)
Trata-se, portanto, de um movimento retilíneo uniformemente acelerado, pois a aceleração da partícula é constante, igual a −2m/s2 (no Sistema Internacional de Unidades).
(b) Para determinarmos os instantes nos quais a partícula passa pela origem, devemos
impor a condição x = 0, ou seja, devemos encontrar as raízes do polinômio x =
0.1 Problemas correspondentes ao Capítulo 2
2
−t2 + 6t + 16. É imediato encontrar os instantes t1 = −2s e t2 = 8s. Como a
partícula começou seu movimento apenas em t=0, significa que a partícula passou
pela origem apenas no instante t2 = 8s.
Como conhecemos a velocidade da partícula, dada pela equação (0.2) sua velocidade, vx2 , nesse instante, é dada por
vx2 = −2 × (8) + 6
=⇒
vx2 = −10m/s .
(0.4)
(c) Note que em função de suas raízes, o polinômio do segundo grau x = −t2 + 6t + 16
se escreve x = −(t + 2)(t − 8). Essa expressão torna evidente que x > 0 se
−2 < t < 8 e x < 0 se t < −2 ou t > 8. Portanto, a partícula permaneceria no
semi-eixo OX positivo (x > 0) no intervalo de tempo (−2, 8). No nosso caso nos
instantes tais que 0 < t < 8.
A equação da posição descreve uma parábola com concavidade para baixo e que
atinge seu máximo no ponto médio entre t = −2s e t = 8s. Portanto, o ponto mais
afastado da origem no semi-eixo positivo ocorrerá em t = 3s.
x(3) = −(3)2 + 6 × 3 + 16 = 25 ,
(0.5)
ou seja, a maior distância da origem atingida pela partícula no intervalo em que ela
se move no semi-eixo OX positivo é igual a 25m. Graficamente, temos para a posição da partícula (x versus t) a seguinte parábola (confira no gráfico as afirmativas
anteriores):
0.1 Problemas correspondentes ao Capítulo 2
3
x = fx (t)
25
8
3
3.
t
(a) Da definição de aceleração, temos dvx /dt = ax . Integrando essa equação, obtemos
(sempre que omitirmos as unidades, estará implícito o uso do SI)
Z t
Z t
′
vx − vx0 =
ax dt =
1 dt′ =⇒ vx = vx0 + t ,
0
(0.6)
0
onde a velocidade inicial será calculada com as condições dadas no problema. Analogamente, da definição de velocidade, temos dx/dt = vx , de modo que integrando
uma vez mais no tempo, obtemos
Z t
Z t
′
(vx0 + t′ ) dt′
vx dt =
x − x0 =
0
=⇒
0
1
x = d + vx0 t + t2 ,
2
(0.7)
onde usamos o fato de que x0 = d. Devemos, agora, utilizar a condição de que para
t′ = 4 a partícula se encontra na posição x′ = d − 6. Impondo essa condição, temos
d − 6 = d + 2vx0 + 2
=⇒
vx0 = −4 ,
(0.8)
e, conseqüentemente, a posição e a velocidade da partícula são dadas, respectivamente, por
1
x(t) = d − 4t + t2
2
vx (t) = t − 4 .
(0.9)
(0.10)
(b) A partícula inverte o sentido de seu movimento a partir do instante em que sua
velocidade é nula, isto é, em ti = 4s. Sabemos que, de fato, ela inverte o sentido de
seu movimento nesse instante pois sua velocidade muda de sinal em t = 4s.
0.1 Problemas correspondentes ao Capítulo 2
4
Para sabermos em que instante ela retorna à posição inicial, basta forçarmos que
sua posição seja igual a d, ou seja, d−4t+t2 /2 = d. Descartando, por razões óbvias,
o valor t = 0s, concluímos que ela retorna à posição inicial no instante t = 8s.
Observe que a partícula gasta 4s até parar e outros 4s até retornar à posição inicial.
Isso já era esperado, pois trata-se de um MRUV (o mesmo ocorre no movimento de
queda livre, no qual o tempo de subido é sempre igual ao tempo de descida).
(c) A condição para que a partícula não atinja o semi-eixo OX negativo é x > 0 para
qualquer instante de tempo. Como a x = d − 4t + t2 /2 corresponde a uma parábola
cuja parte côncava está do lado do semi-eixo OX positivo (pois o coeficiente que
acompanha o termo quadrático é positivo) o ponto mais próximo da origem (nos
casos em que não atinge a origem) é o vértice da parábola. Esse vértice ocorre no
instante ti = 4seg, no qual a partícula inverte o sentido de seu movimento (quando
sua velocidade é nula). Portanto, devemos impor a condição:
1
d − 4ti + t2i > 0
2
=⇒
(0.11)
d > 8m .
4. Escolhendo o eixo OY com direção vertical, apontando para cima e com a origem no
ponto de lançamento da partícula, a posição e a velocidade da partícula são dadas, respectivamente, por
1
y = v0 t − gt2
2
e
(0.12)
vy = v0 − gt ,
onde escolhemos t = 0 como o instante de lançamento e denotamos por g o módulo
da aceleração gravitacional na superfície terrestre. Quando a partícula atinge a altura
máxima de sua trajetória, sua velocidade é nula. Conseqüentemente, da última equação
obtemos o tempo de subida, ts , impondo a condição vy = 0 = v0 − gts , o que nos leva a
ts = v0 /g. Seja t1 = ts /2 = v0 /2g. A distância percorrida no intervalode tempo [0, t1 ] é
dada, então, por
d 1 = y1 − 0 = v 0
v0
2g
g
−
2
v0
2g
2
=⇒
d1 =
3v02
,
8g
(0.13)
onde a posição da partícula no instante t1 , y1 , foi calculada a partir da primeira equação
escrita em Eq(0.12). O instante final do segundo intervalo de tempo a ser considerado é
0.1 Problemas correspondentes ao Capítulo 2
5
justamente ts . A posição da particula, nesse instante, é ys = v0 (v0 /g) − (g/2)(v0 /g)2 .
Com isso, a distância percorrida no intervalo de tempo [t1 = ts /2, ts ] é dada por
2
g v0
v2
v0
−
− d1 =⇒ d2 = 0 .
d 2 = yf − d 1 = v 0
g
2 g
8g
(0.14)
Dessa forma, obtemos, para a razão desejada, o resultado
d1
3v 2 8g
= 0 2 =3 .
d2
8g v0
(0.15)
Note que esse resultado independe de v0 , ou seja, ocorre em qualquer lançamento
vertical. Como o tempo de subida é igual ao de descida, a distância percorrida pela partícula na primeira metade do tempo de descida é 1/3 da distância percorrida na segunda
metade.
5. Por conveniência, escolheremos o eixo OY vertical, apontando para baixo e com a origem
no alto do prédio, ou seja, na posição de onde a pedra foi abandonada a partir do repouso
no instante inicial t0 = 0. Com essa escolha, a posição da pedra é dada por
1
y(t) = gt2 .
2
(0.16)
Seja t1 o instante em que a pedra está a uma distância de 25 metros acima do solo.
Como ela demora 1 segundo a partir de t1 para atingir o solo, podemos escrever
y(t1 + 1) − y(t1 ) = 25 .
(0.17)
Utilizando a equação (0.16), a condição anterior toma a forma
1
1
g(t1 + 1)2 − g(t1 )2 = 25 ,
2
2
(0.18)
ou seja,
1
g t1 +
2
= 25 .
(0.19)
Substituindo o valor de g, temos, t1 = 2s. Uma vez que a pedra partiu do repouso em
t0 = 0 e atingiu o solo no instante t1 + 1 = 3s, a altura do prédio, h, é dada por
1
h = y(t1 + 1) = g(t1 + 1)2 = 45 m .
2
(0.20)
0.1 Problemas correspondentes ao Capítulo 2
6
6. Para facilitar a compreensão dos gráficos, repetimos o de posição versus tempo e exibimos
os gráficos de velocidade e aceleração versus tempo logo abaixo deste.
x
t1
t2
t1
t2
t
vx
t
ax
t1
t2
t
ax1
0.1 Problemas correspondentes ao Capítulo 2
7
A construção do gráfico vx versus t se baseia na análise da inclinação das retas tangentes
ao gráfico x versus t em cada ponto. A inclinação da reta tangente em cada ponto do
gráfico da posição corresponde ao valor da derivada dessa função, nesse ponto, ou seja,
a dx/dt, que é exatamente a sua velocidade. Resumidamente, dizemos que a velocidade,
num dado instante de tempo, descreve a inclinação do gráfico x versus t, nesse instante.
Assim, a velocidade no intervalo 0 ≤ t ≤ t1 diminui de um valor positivo até o valor
nulo, pois o gráfico xversus t diminui sua inclinação no intervalo 0 < t < t1 , começando
por um valor positivo qualquer em t = 0 e terminando com o valor nulo em t = t1 . No
intervalo t1 < t < t2 , a velocidade se torna negativa, mas seu módulo aumenta pois as
inclinações das retas tangentes ao gráfico xversus t aumentam em módulo. Para t > t2 a
inclinação do gráfico x versus t começa a diminuir em módulo, mas sempre assumindo
valores negativos. Desse modo, a velocidade alcança um mínimo em t = t2 . Para valores
de t muito grandes a inclinação do gráfico x versus t é cada vez menor em módulo, mas
sempre negativa, o que significa que para t > t2 a velocidade tende assintoticamente a
zero (por valores negativos).
De forma análoga é a construção do gráfico ax versus t, pois se baseia na análise
da inclinação das retas tangentes ao gráfico vx versus t em cada ponto. A inclinação da
reta tangente em cada ponto do gráfico da velocidade corresponde, agora, ao valor da
derivada dessa função nesse ponto, ou seja, a dvx /dt, que é exatamente a aceleração. Portanto, resumidamente, dizemos que a aceleração, num dado instante de tempo, descreve
a inclinação do gráfico vx versus t, nesse instante.
Note, que os máximos locais (ou mínimos locais) do gráfico x versus t correspondem aos pontos de retorno do movimento onde a velocidade é nula (derivada nula). Um
exemplo de ponto de retorno ocorre em t1 no gráfico mostrado. Por outro lado, máximos
locais (ou mínimos locais) do gráfico vx versus t correspondem a pontos de inflexão do
gráfico x versus t, i.e., pontos onde o gráfico da posição muda de concavidade. Esses
pontos indicam que a aceleração da partícula muda de sinal: por exemplo, uma partícula
0.1 Problemas correspondentes ao Capítulo 2
8
inicialmente acelerada, que vai diminuindo sua aceleração até que, a partir de um dado
instante (ponto de inflexão do gráfico de x versus t) passa a ser freada. Em outras palavras, à direita do ponto de inflexão a aceleração tem um sinal e à direita, o sinal oposto.
Exemplo de um ponto de inflexão ocorre no instante t2 .
7. Num gráfico de velocidade versus tempo, a área algebrica sob o gráfico é igual ao deslocamento da partícula no intervalo em consideração. No caso em questão, as respectivas
áreas sob os gráficos das velocidades de Pedro e Renata são iguais, pois ambos os triângulos têm a mesma base (tempo tf )e a mesma altura (a velocidade máxima vm ). Como
velocidade média é, por definição, hvi = ∆s/∆t, concluímos que vR = vP .
8.
(a) O gráfico pedido neste item corresponde ao feito com a linha contínua (o trecho com
a linha tracejada será útil na explicação do próximo item).
v
inclinação −β
inclinação α
área = d
O
t′′ t′
t
(b) Como a área sob a curva do gráfico de vx versus t no intervalo [0, t′ ] representa
a distância d percorrida pelo carro nesse intervalo, para que ele percorra a mesma
distância num intervalo de tempo menor ele deve seguir um movimento no qual
retorne ao repouso num instante menor que t′ (por exemplo, o instante t′′ da figura),
e que tenha a mesma área sob a nova curva vx versus t. No entanto, para que no
intervalo [0, t′′ ] a nova área sob o gráfico seja a mesma que antes, a desaceleração (ou
a aceleração) deve necessariamente superar o valor máximo permitido. Considere,
por exemplo, o movimento formado pela semireta que sai da origem até a velocidade
máxima e a linha pontilhada até o repouso. Observe, então, que, para compensar a
0.1 Problemas correspondentes ao Capítulo 2
9
área perdida no final do movimento, a curva pontilhada tem obrigatoriamente algum
trecho no qual as inclinações são superiores a β.
9.
(a) O movimento da partícula muda de sentido quando sua velocidade muda de sinal.
Para que isso ocorra a sua velocidade deve, necessariamente, passar pelo valor nulo
(esta é uma condição necessária, mas não suficiente, pois a velocidade de uma partícula pode diminuir, se anular e voltar a crescer sem inverter o sentido do movimento). No caso em questão, a partícula inverte o sentido de seu movimento
duas vezes, em t = 1 e t = 3, instantes que correspondem às raízes da equação
vx = t2 − 4t + 3 = 0.
(b) Da definição de aceleração e com vx = t2 − 4t + 3, temos
ax = dvx /dt = 2t − 4 .
(0.21)
Portanto, a aceleração da partícula é nula apenas no instante t = 2.
(c) O gráfico de vx versus t é dado por uma parábola com raízes 1 e 3, passando por
um mínimo em 2. Já o gráfico de ax versus t é dado por uma reta com inclinação
positiva e cortando o eixo do tempo em t = 2, como ilustram as figuras
vx
1
O
2
3
t
(d) Da definição de velocidade, temos dx/dt = vx . Integrando essa equação, obtemos
Z t
t3
2
(0.22)
x − x0 =
(t′ − 4t′ + 3) dt′ =⇒ x = − 2t2 + 3t .
3
0
0.1 Problemas correspondentes ao Capítulo 2
10
ax
O
t
2
−4
Observe, inicialmente, que o gráfico a ser desenhado não será uma parábola, pois a
equação anterior contém um termo cúbico no tempo. Lembrando que a velocidade
é o coeficiente angular no gráfico de posição versus tempo, vemos que a inclinação
no gráfico pedido deve diminuir até atingir um valor mínimo (negativo) em t = 2 e,
a partir daí, aumentar indefinidamente. Em t = 1 e t = 3 a inclinação no gráfico
deve ser nula, uma vez que a velocidade da partícula é nula nesses instantes. Além
disso, x = t3 /3−2t2 +3t = 0 apenas em t = 0 e t = 3, isntantes nos quais o gráfico
toca o eixo do tempo (partícula na origem). Confira no gráfico essas informações.
x
O
10.
1
2
3
t
(a) A unidade no SI do produto bt deve ser m/s2 . Logo, a constante b deve ser expressa
em m/s3 . Analogamente, a constante c deve ter unidade de aceleração, ou seja, m/s2 .
0.1 Problemas correspondentes ao Capítulo 2
(b) Da definição de aceleração, temos
Z t
1
dvx
(bt′ − c) dt′ =⇒ vx = bt2 − ct .
= ax =⇒ vx − vx0 =
dt
2
0
11
(0.23)
Nesse caso, a partícula inverte o sentido de seu movimento nos instantes em que a
sua velocidade se anula, ou seja, nos instantes t = 0 e t = 2c/b.
(c) Da definição de velocidade, temos
Z t
1
1
1 ′2
dx
′
= vx =⇒ x − x0 =
bt − ct dt′ =⇒ x = bt3 − ct2 . (0.24)
dt
2
6
2
0
É conveniente reescrever a posição como x = t2 (bt/6 − c/2). Dessa forma, é
imediato ver que a partícula está na origem nos instantes t = 0 e t = 3c/b. No
entanto, em t = 0 ela não cruza a origem, pois nesse instante, como vimos no
intem anterior, ela inverte o sentido de seu movimento. Portanto, ela cruza a origem
apenas no instante t = 3c/b (o gráfico mostrado no próximo item ilustra com clareza
o movimento da partícula).
(d) Para tempos negativos, a partícula está se aproximando da origem com velocidades
positivas de módulo cada vez menor. Em t = 0 ela está na origem e tem velocidade
nula pois, como já vimos, nesse instante ela inverte o sentido de seu movimento.
Como no intervalo 0 < t < c/b sua aceleração é negativa, nesse intervalo sua
velocidade é também negativa e de módulo crescente. No instante t = c/b sua
aceleração é nula e, a partir daí, sua aceleração é sempre positiva e cada vez maior.
Com isso, em t = c/b a velocidade passa por um mínimo e o gráfico de x versus
t tem inclinação negativa de maior valor. Entre t = c/b e t = 2c/b a inclinação
no gráfico da posição diminui em módulo, se anulando em t = 2c/b. A partir de
t = 2c/b essa inclinação cresce indefinidamente. A partícula cruza a origem no
instante t = 3c/b.
0.1 Problemas correspondentes ao Capítulo 2
12
x
O
c/b
2c/b
3c/b
vx = 0
t