TC – 2º Ano Olímpico Professor: Eduardo Kilder 01 ) (Unicamp

TC – 2º Ano Olímpico
Professor: Eduardo Kilder
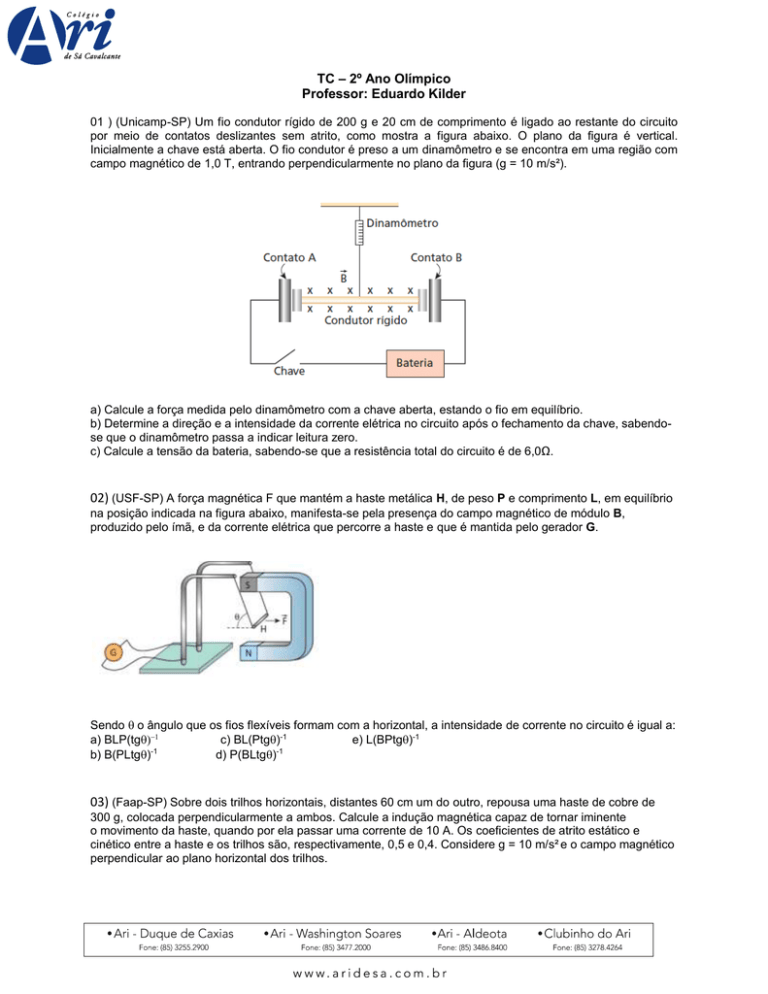
01 ) (Unicamp-SP) Um fio condutor rígido de 200 g e 20 cm de comprimento é ligado ao restante do circuito
por meio de contatos deslizantes sem atrito, como mostra a figura abaixo. O plano da figura é vertical.
Inicialmente a chave está aberta. O fio condutor é preso a um dinamômetro e se encontra em uma região com
campo magnético de 1,0 T, entrando perpendicularmente no plano da figura (g = 10 m/s²).
a) Calcule a força medida pelo dinamômetro com a chave aberta, estando o fio em equilíbrio.
b) Determine a direção e a intensidade da corrente elétrica no circuito após o fechamento da chave, sabendose que o dinamômetro passa a indicar leitura zero.
c) Calcule a tensão da bateria, sabendo-se que a resistência total do circuito é de 6,0Ω.
02) (USF-SP) A força magnética F que mantém a haste metálica H, de peso P e comprimento L, em equilíbrio
na posição indicada na figura abaixo, manifesta-se pela presença do campo magnético de módulo B,
produzido pelo ímã, e da corrente elétrica que percorre a haste e que é mantida pelo gerador G.
Sendo o ângulo que os fios flexíveis formam com a horizontal, a intensidade de corrente no circuito é igual a:
a) BLP(tg c) BL(Ptg)-1
e) L(BPtg)-1
-1
-1
b) B(PLtg)
d) P(BLtg)
03) (Faap-SP) Sobre dois trilhos horizontais, distantes 60 cm um do outro, repousa uma haste de cobre de
300 g, colocada perpendicularmente a ambos. Calcule a indução magnética capaz de tornar iminente
o movimento da haste, quando por ela passar uma corrente de 10 A. Os coeficientes de atrito estático e
cinético entre a haste e os trilhos são, respectivamente, 0,5 e 0,4. Considere g = 10 m/s² e o campo magnético
perpendicular ao plano horizontal dos trilhos.
04) Uma barra metálica de 2 N de peso apoia-se sobre dois trilhos, também metálicos, que formam 45° com o
plano horizontal. A distância entre os trilhos é de 1 m e suas extremidades superiores estão ligadas a uma
bateria. Nessa região do espaço existe um campo magnético uniforme e vertical dirigido de baixo para cima e
definido, em cada ponto, pelo vetor B, de módulo igual a 0,5 tesla. O atrito é considerado nulo.
05) No esquema da figura, a barra AB tem resistência R = 9 Ω, peso de módulo P = 20 N e comprimento L = 1
m. Essa barra faz contato praticamente sem atrito com dois trilhos verticais MN e M’N’, perfeitamente
condutores. Perpendicularmente ao plano dos trilhos, existe um campo de indução magnética uniforme e
constante de intensidade B = 0,5 T. Sabendo que a barra AB mantém-se em repouso, determine a força
eletromotriz do gerador.
06) Uma barra de material isolante, em forma de um “V”, pode girar livremente em torno de um eixo que passa
por O. Na extremidade direita da barra está suspenso um prato, em que poderão ser colocadas massas
conhecidas. Na parte esquerda da barra é fixado um fio condutor rígido ABCDEF, cujos terminais são A e F.
Os trechos BC e DE do fio são arcos de circunferência com centros em O. A região CD desse fio, de
comprimento 5,00 cm, está imersa em um campo magnético uniforme B, perpendicular ao plano da figura e
apontando para o leitor. O sistema descrito, inicialmente em equilíbrio, permite medir a intensidade
de B. Para isso, usando fios muito flexíveis, que não perturbem o equilíbrio do sistema, ligamos os terminais A
e F a um gerador em série com um medidor de corrente. Suponha que o sentido da corrente em CD seja de C
para D e que sua intensidade seja 10,0 A. Estabelecida essa corrente, o sistema desequilibra-se, sendo
necessário colocar uma massa de 15,0 g no prato para que o equilíbrio se restabeleça. Sendo g = 9,80 m/s²,
calcule a intensidade de B.
07) O espectrômetro de massa é um instrumento usado na determinação de massas atômicas e também na
separação de isótopos de um mesmo elemento químico. A figura mostra esquematicamente um
tipo de espectrômetro. A fonte produz íons que emergem dela com carga +e e são acelerados por um campo
elétrico não indicado na figura. As fendas F1 e F2 servem para colimar o feixe de íons, isto é, para que
prossigam apenas íons que se movem em uma determinada direção. Os íons que passam pela fenda F 2
invadem o seletor de velocidade, que é uma região onde existem um campo elétrico e um campo magnético,
ambos uniformes e constantes, perpendiculares entre si e perpendiculares ao feixe de íons. Só prosseguem
na mesma trajetória retilínea os íons que têm determinada velocidade v . Os íons que atravessam a
fenda F3 entram em movimento circular e uniforme de raio R.
Considerando E = 4,0 · 10³ N/C, B = 2,0 · 10-1 T e R = 2,0 · 10-2 m e sendo e = 1,6 · 10-19 C, determine a massa
do íon.
08) (UFPE) Partículas de massa m = 1,6 · 10-26 kg e carga q = 1,6 · 10-19C, após serem aceleradas desde o
repouso por uma diferença de potencial de 2 000 V, entram em um campo magnético igual a 0,5 T,
perpendicular à direção de seus movimentos. Qual é o raio de suas trajetórias, em milímetros?
09) Uma bolinha de massa m = 2,0 · 10-3kg, eletrizada com carga q = 8,0 · 10-6 C, move-se em linha reta em
um plano horizontal, com velocidade constante de 2,0 · 10-2 m/s. Ao passar pelo ponto A, a bolinha penetra
numa região onde existe um campo magnético uniforme e vertical, de intensidade 5,0 T (extremamente
maior que o campo magnético terrestre), que se estende até a parede vertical. Desprezando o atrito e as influências do ar, a que distância do ponto B a bolinha colidirá com a parede vertical?
10) (ITA-SP) Uma partícula de massa m carregada com carga q  0 encontra-se inicialmente em repouso
imersa num campo gravitacional g e num campo magnético B0 com sentido negativo em relação ao eixo
Oz, conforme indicado na figura. Sabemos que a velocidade e a aceleração da partícula na direção
Oy são funções harmônicas simples. Disso resulta uma trajetória cicloidal num plano perpendicular
a B0. Determine o deslocamento máximo (L) da partícula.
11) No cobre, o número de elétrons livres por unidade de volume é n = 8,5 · 1022elétrons/cm3. Na figura a
seguir temos uma f ita de cobre, percorrida por corrente constante de intensidade i = 100 A e imersa em
campo magnético uniforme de intensidade B = 4,0 T, perpendicular a ela. Calcule:
a) a velocidade média de deslocamento dos elétrons livres (e = 1,6 · 10-19 C);
b) a diferença de potencial entre os pontos P e Q, em valor absoluto.
12) (Fuvest-SP) Uma partícula, de massa m e com carga elétrica Q, cai verticalmente com velocidade
constante v0. Nessas condições, a força de resistência do ar pode ser considerada Rar = k v, sendo k uma
constante e v a velocidade. A partícula penetra, então, em uma região onde atua um campo magnético
uniforme e constante B , perpendicular ao plano do papel e, nele entrando, conforme a f igura a seguir. A
velocidade da partícula é, então, alterada, adquirindo, após certo intervalo de tempo, um novo valor vL,
constante.
(Lembre-se de que a intensidade da força magnética é |FM| = |q| |v| |B|, em unidades SI, para v perpendicular a
B .)
a) Expresse o valor da constante k em função de m, g e v0.
b) Esquematize os vetores das forças (Peso, Rar e FM) que agem sobre a partícula, em presença do campo B,
na situação em que a velocidade passa a ser a velocidade vL. Represente, por uma linha tracejada, a direção
e o sentido de vL.
c) Expresse o valor da velocidade vL da partícula, na região onde atua o campo B, em função de m, g, k, B e
Q.