Conversão de Energia I

Departamento de Engenharia Elétrica
Conversão de Energia I
Aula 5.5
Máquinas de Corrente Contínua
Prof. Clodomiro Unsihuay-Vila
Bibliografia
FITZGERALD, A. E., KINGSLEY Jr. C. E UMANS, S. D. Máquinas Elétricas:
com Introdução à Eletrônica De Potência. 6ª Edição, Bookman, 2006.
Capítulo 7 – Máquinas CC
KOSOW, I. Máquinas Elétricas e Transformadores.
Editora Globo. 1986.
Capítulo 3 – Relação de Tensão nas Máquinas CC –
Geradores CC
TORO, V. Del, MARTINS, O. A. Fundamentos de Máquinas
Elétricas. LTC, 1999.
Capítulo 7 – Geradores de Corrente Contínua;
Bim, Edson. Máquinas Elétricas e Acionamento.
Editora Elsevier, 2009.
Capítulo 7 – Regime permanente de máquinas de
corrente contínua
Conversão de Energia I
Tipos de Geradores de Corrente Contínua
Gerador com excitação composta
Representação da forma de
ligação do enrolamento de
campo para um gerador com
excitação composta.
Conversão de Energia I
Tipos de Geradores de Corrente Contínua
Gerador com excitação composta
Operando como gerador a tensão
apresenta uma boa regulação perto da
potência nominais.
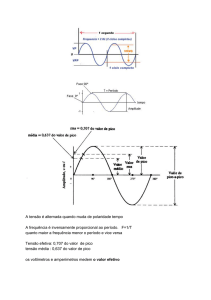
(↑ E ) = K ⋅ (↑ φ )⋅ w
a
Z
pico
m
Para baixas correntes de armadura o
fluxo magnético de campo fica baixo, o
que compromete a geração com
cargas de baixa potência.
Dependendo da relação entre as
espiras do campo série e do campo
em derivação, podemos obter os
comportamentos apresentados ao
lado.
Conversão de Energia I
Tipos de Geradores de Corrente Contínua
Gerador com excitação composta
Ligação em derivação longa de
um gerador ou motor composto.
Fmm produzida pelo enrolamento
de campo.
Fmmcampo = N S ⋅ I a + N f ⋅ I f
Qual é a corrente no enrolamento em derivação que produz a mesma
Fmm de campo produzida pelos enrolamentos série e derivação.
I shut _ equi
Conversão de Energia I
NS
=
⋅ Ia + I f
Nf
Tipos de Geradores de Corrente Contínua
Gerador com excitação composta
Ligação em derivação curta
de um gerador composto.
Fmm produzida pelo enrolamento
de campo.
Fmmcampo = N S ⋅ I S + N f ⋅ I f
Qual é a corrente no enrolamento em derivação que produz a mesma
Fmm de campo produzida pelos enrolamentos série e derivação.
I shut _ equi
Conversão de Energia I
NS
=
⋅ IS + I f
Nf
Exercícios
Um gerador composto de 100 [kW], 250 [V] e 400 [A], com uma ligação em
derivação longa, tem a resistência de armadura (incluindo as escovas) de
0,025 [Ω], a resistência de campo em série de 0,005 [Ω] e a curva de
magnetização apresentada na figura abaixo. Há um campo em derivação
com 1000 espiras por pólo e um campo em série de três espiras por pólo.
O campo em série é ligado de tal modo que uma corrente positiva de
armadura produz um Fmm no eixo direto que se soma à do campo em
derivação.
Calcule a tensão de terminal,
para a corrente nominal de
terminal, quando a corrente de
campo em derivação é 4,7 [A] e a
velocidade
é
1150
[rpm].
Despreze os efeitos da reação de
armadura. ( Vt = 251 [V])
Conversão de Energia I
Exercício
Um gerador composto de 100 [kW], 250 [V] e 400 [A], com uma ligação em
derivação longa, tem a resistência de armadura (incluindo as escovas) de
0,025 [Ω], a resistência de campo em série de 0,005 [Ω] e a curva de
magnetização apresentada na figura abaixo. Há um campo em derivação
com 1000 espiras por pólo e um campo em série de três espiras por pólo.
O campo em série é ligado de tal modo que uma corrente positiva de
armadura produz um Fmm no eixo direto que se soma à do campo em
derivação.
Calcule a tensão de terminal,
para a corrente nominal de
terminal, quando a corrente de
campo em derivação é 4,7 [A] e a
velocidade
é
1150
[rpm].
Considerar os efeitos da
reação de armadura.
(Vt = 238 [V] )
Conversão de Energia I
Exercício
Um gerador CC shunt de 12 [kW], 100 [V], 1000 [rpm] tem uma
resistência de armadura Ra = 0,1 [Ω], a resistência do enrolamento de
campo Rfw = 80 [Ω], e Nf = 1200 espiras por pólo. As características de
magnetização para 1000 [rpm] é apresentada abaixo. O gerador está
operando com uma velocidade de rotação de 1000 [rpm]. A reação de
armadura para carga nominal é de 0,06 [A].
Na máquina acima foi inserido um enrolamento em série para que opere
como uma máquina CC composta. Deseja-se que a máquina forneça
uma tensão terminal de 100 [V] sem carga e também com carga nominal
(regulação igual a zero). Quantas espiras no enrolamento série são
necessárias para obter a regulação igual a zero. Assumindo uma
conexão curta do gerador composto e que a resistência do enrolamento
série é Rsr =0,01 Ω.
Conversão de Energia I
Exercício
Conversão de Energia I
Exercício
Na máquina acima foi inserido um enrolamento em série para que opere
como uma máquina CC composta. Deseja-se que a máquina forneça
uma tensão terminal de 100 [V] sem carga e também com carga nominal
(regulação igual a zero). Quantas espiras no enrolamento série são
necessárias para obter a regulação igual a zero. Assumindo uma
conexão curta do gerador composto e que a resistência do enrolamento
série é Rsr =0,01 Ω.
Em exercícios anteriores vimos que um
Rf = 100 Ω produz a tensão a vazio de
100 [V]. (vazio não há corrente no
enrolamento série)
Conversão de Energia I
Exercício
Na máquina acima foi inserido um enrolamento em série para que opere
como uma máquina CC composta. Deseja-se que a máquina forneça
uma tensão terminal de 100 [V] sem carga e também com carga nominal
(regulação igual a zero). Quantas espiras no enrolamento série são
necessárias para obter a regulação igual a zero. Assumindo uma
conexão curta do gerador composto e que a resistência do enrolamento
série é Rsr =0,01 Ω.
Da curva de magnetização
podemos determinar a
corrente
de
campo
necessária para produzir
uma tensão de armadura
de 113,2 [V].
I f = 1,45[ A]
Conversão de Energia I
Motores de Corrente Contínua
Determinação da velocidade de rotação do motor
Va = Ea + Ra ⋅ I a
Ea = K Z ⋅ φ pico ⋅ wm
VF = RF ⋅ I F
⇒ φ = função ( I F )
T = K Z ⋅ φ pico ⋅ I a
T
⇔ Ia =
K Z ⋅ φ pico
Conversão de Energia I
Motores de Corrente Contínua
Determinação da velocidade de rotação do motor
Va = Ea + Ra ⋅ I a
⇒
Ea = Va − Ra ⋅ I a
T
Ea = Va − Ra ⋅ I a ⇒ K Z ⋅ φ pico ⋅ wm = Va − Ra ⋅
K Z ⋅ φ pico
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
Conversão de Energia I
Motores de Corrente Contínua
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
T = K Z ⋅ φ pico ⋅ I a
Ea = K Z ⋅ φ pico ⋅ wm
Conversão de Energia I
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
a) Reduzindo à metade a tensão de terminal de armadura enquanto o
fluxo de campo e o conjugado da carga permanecem constantes;
b) Reduzindo à metade a tensão de terminal de armadura enquanto a
corrente de campo e a potência da carga permanecem constante;
c) Dobrando o fluxo de campo enquanto a tensão de terminal de armadura
e o conjugado da carga permanecem constantes;
d) Reduzindo à metade ambos o fluxo de campo e a tensão de terminal de
armadura enquanto a potência da carga permanece constante;
e) Reduzindo à metade a tensão de terminal de armadura enquanto o
fluxo de campo permanece constante e o conjugado da carga varia
segundo o quadrado da velocidade.
Conversão de Energia I
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
a) Reduzindo à metade a tensão de terminal de armadura enquanto o
fluxo de campo e o conjugado da carga permanecem constantes;
Ea = K Z ⋅ φ pico ⋅ wm
T = K Z ⋅ φ pico ⋅ I a
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
wm = a velocidade reduz
aproximadamente a metade;
Ia = permanece constante.
Conversão de Energia I
a
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
b) Reduzindo à metade a tensão de terminal de armadura enquanto a
corrente de campo e a potência da carga permanecem constante;
Ea = K Z ⋅ φ pico ⋅ wm
T = K Z ⋅ φ pico ⋅ I a
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
wm
=
a
velocidade
reduz
aproximadamente a metade;
Ia = dobra o valor da corrente;
T = dobra o valor do torque.
Conversão de Energia I
a
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
c) Dobrando o fluxo de campo enquanto a tensão de terminal de armadura
e o conjugado da carga permanecem constantes;
Ea = K Z ⋅ φ pico ⋅ wm
T = K Z ⋅ φ pico ⋅ I a
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
wm
=
a
velocidade
reduz
aproximadamente a metade;
Ia = a corrente reduz a metade.
Conversão de Energia I
a
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
d) Reduzindo à metade ambos o fluxo de campo e a tensão de terminal de
armadura enquanto a potência da carga permanece constante;
Ea = K Z ⋅ φ pico ⋅ wm
T = K Z ⋅ φ pico ⋅ I a
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
wm = a velocidade permanece constante;
Ia = dobra o valor da corrente.
Conversão de Energia I
Exercício
Para cada uma das seguintes mudanças nas condições de operação de
um motor CC com excitação independente, descreva como a corrente de
armadura e a velocidade irão variar:
e) Reduzindo à metade a tensão de terminal de armadura enquanto o
fluxo de campo permanece constante e o conjugado da carga varia
segundo o quadrado da velocidade.
Ea = K Z ⋅ φ pico ⋅ wm
T = K Z ⋅ φ pico ⋅ I a
Va
Ra
wm =
−
⋅T
2
K Z ⋅ φ pico (K Z ⋅ φ pico )
wm
=
a
velocidade
reduz
aproximadamente a metade;
Ia = reduz a um quarto da corrente.
Conversão de Energia I
a
Exercícios
Utilizando um sistema para variação de velocidade de um motor CC com
excitação independente através da variação da tensão da fonte de alimentação
(tensão terminal). O torque e o perfil de tensão são apresentados na figura abaixo.
O controle de velocidade opera numa faixa de 0 a 1500 [rpm] através da variação
da tensão terminal de 0 a 500 [V], mantendo a corrente de campo constante.
a) Determine a corrente de armadura do motor
se o torque permanece constante em 300
[N.m] de 0 até a velocidade de 1500 [rpm].
b) Para velocidades acima de 1500 [rpm] o
controle de velocidade é obtido pelo
enfraquecimento do campo, mantendo a
tensão de armadura constante em 500 [V].
Determine o torque para uma velocidade de
3000 [rpm] se a corrente de armadura é
mantida constante no valor obtido no item (a).
Negligenciar todas as perdas.
Conversão de Energia I