LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
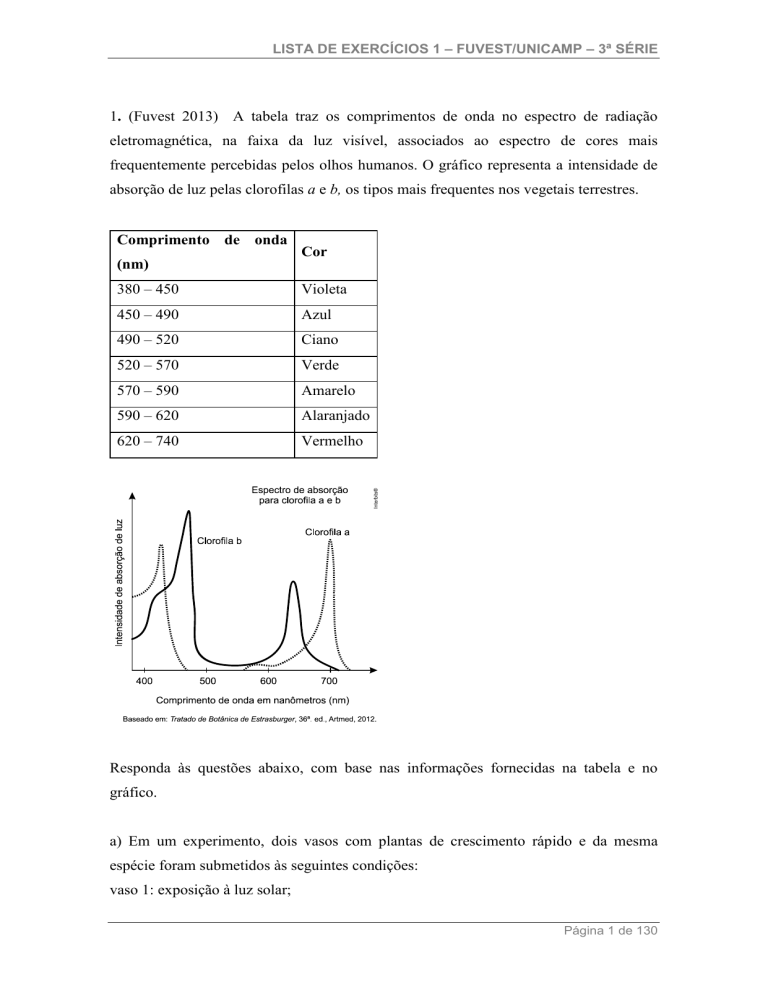
1. (Fuvest 2013) A tabela traz os comprimentos de onda no espectro de radiação
eletromagnética, na faixa da luz visível, associados ao espectro de cores mais
frequentemente percebidas pelos olhos humanos. O gráfico representa a intensidade de
absorção de luz pelas clorofilas a e b, os tipos mais frequentes nos vegetais terrestres.
Comprimento de onda
(nm)
Cor
380 – 450
Violeta
450 – 490
Azul
490 – 520
Ciano
520 – 570
Verde
570 – 590
Amarelo
590 – 620
Alaranjado
620 – 740
Vermelho
Responda às questões abaixo, com base nas informações fornecidas na tabela e no
gráfico.
a) Em um experimento, dois vasos com plantas de crescimento rápido e da mesma
espécie foram submetidos às seguintes condições:
vaso 1: exposição à luz solar;
Página 1 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
vaso 2: exposição à luz verde.
A temperatura e a disponibilidade hídrica foram as mesmas para os dois vasos. Depois
de algumas semanas, verificou-se que o crescimento das plantas diferiu entre os vasos.
Qual a razão dessa diferença?
b) Por que as pessoas, com visão normal para cores, enxergam como verdes, as folhas
da maioria das plantas?
2. (Fuvest 2012) Num ambiente iluminado, ao focalizar um objeto distante, o olho
humano se ajusta a essa situação. Se a pessoa passa, em seguida, para um ambiente de
penumbra, ao focalizar um objeto próximo, a íris
a) aumenta, diminuindo a abertura da pupila, e os músculos ciliares se contraem,
aumentando o poder refrativo do cristalino.
b) diminui, aumentando a abertura da pupila, e os músculos ciliares se contraem,
aumentando o poder refrativo do cristalino.
c) diminui, aumentando a abertura da pupila, e os músculos ciliares se relaxam,
aumentando o poder refrativo do cristalino.
d) aumenta, diminuindo a abertura da pupila, e os músculos ciliares se relaxam,
diminuindo o poder refrativo do cristalino.
e) diminui, aumentando a abertura da pupila, e os músculos ciliares se relaxam,
diminuindo o poder refrativo do cristalino.
3. (Unicamp 2015) Movimento browniano é o deslocamento aleatório de partículas
microscópicas suspensas em um fluido, devido às colisões com moléculas do fluido em
agitação térmica.
a) A figura abaixo mostra a trajetória de uma partícula em movimento browniano em
um líquido após várias colisões. Sabendo-se que os pontos negros correspondem a
posições da partícula a cada 30s, qual é o módulo da velocidade média desta partícula
entre as posições A e B?
b) Em um de seus famosos trabalhos, Einstein propôs uma teoria microscópica para
explicar o movimento de partículas sujeitas ao movimento browniano. Segundo essa
teoria, o valor eficaz do deslocamento de uma partícula em uma dimensão é dado por
Página 2 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
I 2 D t, onde t é o tempo em segundos e D kT r é o coeficiente de difusão de uma
partícula em um determinado fluido, em que k 3 1018 m3 sK, T é a temperatura
absoluta e r é o raio da partícula em suspensão. Qual é o deslocamento eficaz de uma
partícula de raio r 3μm neste fluido a T 300K após 10 minutos?
4. (Unicamp 2015) Os astrônomos estimam que a estrela estaria situada a uma distância
d 9,0 1018 m da Terra. Considerando um foguete que se desloca a uma velocidade
v 1,5 104 m / s, o tempo de viagem do foguete da Terra até essa estrela seria de
(1ano 3,0 107 s)
a) 2.000 anos.
b) 300.000 anos.
c) 6.000.000 anos.
d) 20.000.000 anos.
5. (Unicamp 2015) A Agência Espacial Brasileira está desenvolvendo um veículo
lançador de satélites (VLS) com a finalidade de colocar satélites em órbita ao redor da
Terra. A agência pretende lançar o VLS em 2016, a partir do Centro de Lançamento de
Alcântara, no Maranhão.
a) Considere que, durante um lançamento, o VLS percorre uma distância de 1200km em
800s. Qual é a velocidade média do VLS nesse trecho?
Página 3 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) Suponha que no primeiro estágio do lançamento o VLS suba a partir do repouso com
aceleração resultante constante de módulo aR . Considerando que o primeiro estágio
dura 80s, e que o VLS percorre uma distância de 32km, calcule aR .
6. (Fuvest 2015) O sistema de airbag de um carro é formado por um sensor que detecta
rápidas diminuições de velocidade, uma bolsa inflável e um dispositivo contendo azida
de sódio (NaN3 ) e outras substâncias secundárias. O sensor, ao detectar uma grande
desaceleração, produz uma descarga elétrica que provoca o aquecimento e a
decomposição da azida de sódio. O nitrogênio (N2 ) liberado na reação infla rapidamente
a bolsa, que, então, protege o motorista. Considere a situação em que o carro,
inicialmente a 36 km / h (10 m / s), dirigido por um motorista de 60 kg, para devido a
uma colisão frontal.
a) Nessa colisão, qual é a variação ΔE da energia cinética do motorista?
b) Durante o 0,2 s da interação do motorista com a bolsa, qual é o módulo α da
aceleração média desse motorista?
c) Escreva a reação química de decomposição da azida de sódio formando sódio
metálico e nitrogênio gasoso.
d) Sob pressão atmosférica de 1 atm e temperatura de 27 C, qual é o volume V de gás
nitrogênio formado pela decomposição de 65 g de azida de sódio?
Note e adote:
Desconsidere o intervalo de tempo para a bolsa inflar;
Ao término da interação com a bolsa do airbag, o motorista está em repouso;
Considere o nitrogênio como um gás ideal;
Constante universal dos gases: R 0,08 atm / (mol K);
0 C 273 K.
Página 4 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Elemento
Massa
atômica
(g / mol)
sódio
23
nitrogênio
14
7. (Unicamp 2015)
Considerando que a massa e as dimensões dessa estrela são
comparáveis às da Terra, espera-se que a aceleração da gravidade que atua em corpos
próximos à superfície de ambos os astros seja constante e de valor não muito diferente.
Suponha que um corpo abandonado, a partir do repouso, de uma altura h 54 m da
superfície da estrela, apresente um tempo de queda t 3,0 s. Desta forma, pode-se
afirmar que a aceleração da gravidade na estrela é de
a) 8,0 m / s2.
b) 10 m / s2.
c) 12 m / s2.
d) 18 m / s2.
8. (Fuvest 2015) Uma criança com uma bola nas mãos está sentada em um “gira‐gira”
que roda com velocidade angular constante e frequência f 0,25 Hz.
a) Considerando que a distância da bola ao centro do “gira‐gira” é 2 m, determine os
módulos da velocidade V T e da aceleração a da bola, em relação ao chão.
Num certo instante, a criança arremessa a bola horizontalmente em direção ao centro do
“gira‐gira”, com velocidade VR de módulo 4 m / s, em relação a si.
Determine, para um instante imediatamente após o lançamento,
b) o módulo da velocidade U da bola em relação ao chão;
c) o ângulo θ entre as direções das velocidades U e VR da bola.
Note e adote:
Página 5 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
π3
9. (Unicamp 2015) Considere um computador que armazena informações em um disco
rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um
comprimento físico de 0,2 μm na direção do movimento de rotação do disco. Quantas
informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver
posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado
apresentado abaixo?
(Considere π 3.)
a) 1,62 106.
b) 1,8 106.
c) 64,8 108.
d) 1,08 108.
10. (Fuvest 2015) Uma criança de 30 kg está em repouso no topo de um escorregador
plano de 2,5 m 2,5 m de altura, inclinado 30 em relação ao chão horizontal. Num certo
instante, ela começa a deslizar e percorre todo o escorregador.
Determine
a) a energia cinética E e o módulo Q da quantidade de movimento da criança, na
metade do percurso;
b) o módulo F da força de contato entre a criança e o escorregador;
c) o módulo a da aceleração da criança.
Página 6 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Note e adote:
Forças dissipativas devem ser ignoradas.
A aceleração local da gravidade é 10 m / s2.
sen 30 cos 60 0,5
sen 60 cos 30 0,9
11. (Unicamp 2015) O primeiro trecho do monotrilho de São Paulo, entre as estações
Vila Prudente e Oratório, foi inaugurado em agosto de 2014. Uma das vantagens do
trem utilizado em São Paulo é que cada carro é feito de ligas de alumínio, mais leve que
o aço, o que, ao lado de um motor mais eficiente, permite ao trem atingir uma
velocidade de oitenta quilômetros por hora.
a) A densidade do aço PE daço 7,9g / cm3 e a do alumínio é dAl 2,7g / cm3. Obtenha a
τaço
entre os trabalhos realizados pelas forças resultantes que aceleram dois
τAl
razão
trens de dimensões idênticas, um feito de aço e outro feito de alumínio, com a mesma
aceleração constante de módulo a, por uma mesma distância I.
b) Outra vantagem do monotrilho de São Paulo em relação a outros tipos de transporte
urbano é o menor nível de ruído que ele produz. Considere que o trem emite ondas
esféricas como uma fonte pontual. Se a potência sonora emitida pelo trem é igual a
P 1,2mW, qual é o nível sonoro S em dB, a uma distância R 10m do trem? O nível
I
I0
sonoro S em dB é dado pela expressão S 10dB log , em que I é a intensidade da inda
sonora e I0 1012 W / m2 é a intensidade de referência padrão correspondente ao limiar
da audição do ouvido humano.
12. (Fuvest 2015) A energia necessária para o funcionamento adequado do corpo
humano é obtida a partir de reações químicas de oxidação de substâncias provenientes
da alimentação, que produzem aproximadamente 5 kcal por litro de O2 consumido.
Durante uma corrida, um atleta consumiu 3 litros de O2 por minuto.
Página 7 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Determine
a) a potência P gerada pelo consumo de oxigênio durante a corrida;
b) a quantidade de energia E gerada pelo consumo de oxigênio durante 20 minutos da
corrida;
c) o volume V de oxigênio consumido por minuto se o atleta estivesse em repouso,
considerando que a sua taxa de metabolismo basal é 100 W.
Note e adote:
1cal 4 J.
13. (Fuvest 2015) O espelho principal de um dos maiores telescópios refletores do
mundo, localizado nas Ilhas Canárias, tem 10 m de diâmetro e distância focal de 15 m.
Supondo que, inadvertidamente, o espelho seja apontado diretamente para o Sol,
determine:
a) o diâmetro D da imagem do Sol;
b) a densidade S de potência no plano da imagem, em W / m2;
c) a variação ΔT da temperatura de um disco de alumínio de massa 0,6 kg colocado no
plano da imagem, considerando que ele tenha absorvido toda a energia incidente
durante 4 s.
Note e adote:
π3
O espelho deve ser considerado esférico.
Distância Terra Sol 1,5 1011 m.
Diâmetro do Sol 1,5 109 m.
Calor específico do Al 1 J / (g K). Calor específico do Al = 1 J/(g K).
Densidade de potência solar incidindo sobre o espelho principal do telescópio
1kW / m2.
O diâmetro do disco de alumínio é igual ao da imagem do Sol.
Página 8 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Desconsidere perdas de calor pelo disco de alumínio.
14. (Fuvest 2015)
No desenvolvimento do sistema amortecedor de queda de um
elevador de massa m, o engenheiro projetista impõe que a mola deve se contrair de um
valor máximo d, quando o elevador cai, a partir do repouso, de uma altura h, como
ilustrado na figura abaixo. Para que a exigência do projetista seja satisfeita, a mola a ser
empregada deve ter constante elástica dada por
Note e adote:
- forças dissipativas devem ser ignoradas;
- a aceleração local da gravidade é g.
a) 2 m g h d / d2
b) 2 m g h d / d2
c) 2 m g h / d2
d) m g h / d
e) m g / d
15. (Fuvest 2015) A figura abaixo mostra o gráfico da energia potencial gravitacional
U de uma esfera em uma pista, em função da componente horizontal x da posição da
esfera na pista.
Página 9 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
A esfera é colocada em repouso na pista, na posição de abscissa x x1, tendo energia
mecânica E 0. A partir dessa condição, sua energia cinética tem valor
Note e adote:
- desconsidere efeitos dissipativos.
a) máximo igual a U0 .
b) igual a E quando x x3 .
c) mínimo quando x x2.
d) máximo quando x x3 .
e) máximo quando x x2.
16. (Unicamp 2015) Jetlev é um equipamento de diversão movido a água. Consiste em
um colete conectado a uma mangueira que, por sua vez, está conectada a uma bomba de
água que permanece submersa. O aparelho retira água do mar e a transforma em jatos
para a propulsão do piloto, que pode ser elevado a até 10 metros de altura (ver figura
abaixo).
Página 10 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) Qual é a energia potencial gravitacional, em relação à superfície da água, de um
piloto de 60km, quando elevado a 10 metros de altura?
b) Considere que o volume de água por unidade de tempo que entra na mangueira na
superfície da água é o mesmo que sai nos jatos do colete, e que a bomba retira água do
mar a uma taxa de 30 litros / s. Lembre-se que o Impulso I de uma força constante F,
dado pelo produto desta força pelo intervalo de tempo Δt de sua aplicação I FΔt, é
igual, em módulo, à variação da quantidade de movimento ΔQ do objeto submetido a
esta força. Calcule a diferença de velocidade entre a água que passa pela mangueira e a
que sai nos jatos quando o colete propulsor estiver mantendo o piloto de m 60kg em
repouso acima da superfície da água. Considere somente a massa do piloto e use a
densidade da água ρ 1kg / litro.
17. (Fuvest 2015)
Para impedir que a pressão interna de uma panela de pressão
ultrapasse um certo valor, em sua tampa há um dispositivo formado por um pino
acoplado a um tubo cilíndrico, como esquematizado na figura abaixo. Enquanto a força
resultante sobre o pino for dirigida para baixo, a panela está perfeitamente vedada.
Considere o diâmetro interno do tubo cilíndrico igual a 4 mm e a massa do pino igual a
48 g. Na situação em que apenas a força gravitacional, a pressão atmosférica e a
exercida pelos gases na panela atuam no pino, a pressão absoluta máxima no interior da
panela é
Página 11 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Note e adote:
- π3
- 1atm 105 N / m2
- aceleração local da gravidade 10 m / s2
a) 1,1atm
b) 1,2 atm
c) 1,4 atm
d) 1,8 atm
e) 2,2 atm
18. (Unicamp 2015) Alguns experimentos muito importantes em física, tais como os
realizados em grandes aceleradores de partículas, necessitam de um ambiente com uma
atmosfera extremamente rarefeita, comumente denominada de ultra-alto-vácuo. Em tais
ambientes a pressão é menor ou igual a 106 Pa.
a) Supondo que as moléculas que compõem uma atmosfera de ultra-alto-vácuo estão
distribuídas uniformemente no espaço e se comportam como um gás ideal, qual é o
número de moléculas por unidade de volume em uma atmosfera cuja pressão seja
P 3,2 108 Pa, à temperatura ambiente T 300K? Se necessário, use: Número de
Avogrado NA 6 1023 e a Constante universal dos gases ideais R 8J / molK.
Página 12 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) Sabe-se que a pressão atmosférica diminui com a altitude, de tal forma que, a
centenas de quilômetros de altitude, ela se aproxima do vácuo absoluto. Por outro lado,
pressões acima da encontrada na superfície terrestre podem ser atingidas facilmente em
uma submersão aquática. Calcule a razão Psub Pnave entre as pressões que devem
suportar a carcaça de uma nave espacial (Pnave ) a centenas de quilômetros de altitude e
a de um submarino (Psub ) a 100m de profundidade, supondo que o interior de ambos os
veículos se encontra à pressão de 1atm. Considere a densidade da água como
ρ 1000kg / m3.
19. (Fuvest 2015) Um trabalhador de massa m está em pé, em repouso, sobre uma
plataforma de massa M. O conjunto se move, sem atrito, sobre trilhos horizontais e
retilíneos, com velocidade de módulo constante v. Num certo instante, o trabalhador
começa a caminhar sobre a plataforma e permanece com velocidade de módulo v, em
relação a ela, e com sentido oposto ao do movimento dela em relação aos trilhos. Nessa
situação, o módulo da velocidade da plataforma em relação aos trilhos é
a) 2 m M v / m M
b) 2 m M v / M
c) 2 m M v / m
d) M m v / M
e) m M v / M m
20. (Fuvest 2015)
Página 13 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
O guindaste da figura acima pesa 50.000 N sem carga e os pontos de apoio de suas rodas
no solo horizontal estão em x 0 e x 5 m. O centro de massa (CM) do guindaste sem
carga está localizado na posição (x 3 m, y 2 m). Na situação mostrada na figura, a
maior carga P que esse guindaste pode levantar pesa
a) 7.000 N
b) 50.000 N
c) 75.000 N
d) 100.000 N
e) 150.000 N
21. (Unicamp 2015) A primeira lei de Kepler demonstrou que os planetas se movem
em órbitas elípticas e não circulares. A segunda lei mostrou que os planetas não se
movem a uma velocidade constante.
PERRY, Marvin. Civilização Ocidental: uma história concisa. São Paulo: Martins
Fontes, 1999, p. 289. (Adaptado)
É correto afirmar que as leis de Kepler
a) confirmaram as teorias definidas por Copérnico e são exemplos do modelo científico
que passou a vigorar a partir da Alta Idade Média.
b) confirmaram as teorias defendidas por Ptolomeu e permitiram a produção das cartas
náuticas usadas no período do descobrimento da América.
c) são a base do modelo planetário geocêntrico e se tornaram as premissas cientificas
que vigoram até hoje.
d) forneceram subsídios para demonstrar o modelo planetário heliocêntrico e criticar as
posições defendidas pela Igreja naquela época.
22. (Fuvest 2015) A notícia “Satélite brasileiro cai na Terra após lançamento falhar”,
veiculada pelo jornal O Estado de S. Paulo de 10/12/2013, relata que o satélite CBERS3, desenvolvido em parceria entre Brasil e China, foi lançado no espaço a uma altitude
de 720 km (menor do que a planejada) e com uma velocidade abaixo da necessária para
colocá-lo em órbita em torno da Terra. Para que o satélite pudesse ser colocado em
órbita circular na altitude de 720 km, o módulo de sua velocidade (com direção tangente
à órbita) deveria ser de, aproximadamente,
Página 14 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Note e adote:
- raio da Terra 6 103 km
- massa da Terra 6 1024 kg
- constante da gravitação universal G 6,7 1011 m3 / s2kg
a) 61km / s
b) 25 km / s
c) 11km / s
d) 7,7 km / s
e) 3,3 km / s
23. (Fuvest 2015) Certa quantidade de gás sofre três transformações sucessivas, A B,
B C e C A, conforme o diagrama p V apresentado na figura abaixo.
A respeito dessas transformações, afirmou-se o seguinte:
I. O trabalho total realizado no ciclo ABCA é nulo.
II. A energia interna do gás no estado C é maior que no estado A.
III. Durante a transformação A B, o gás recebe calor e realiza trabalho.
Está correto o que se afirma em:
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
Página 15 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
24. (Fuvest 2015) O desenvolvimento de teorias científicas, geralmente, tem forte
relação com contextos políticos, econômicos, sociais e culturais mais amplos. A
evolução dos conceitos básicos da Termodinâmica ocorre, principalmente, no contexto
a) da Idade Média.
b) das grandes navegações.
c) da Revolução Industrial.
d) do período entre as duas grandes guerras mundiais.
e) da Segunda Guerra Mundial.
25. (Fuvest 2015) Um recipiente hermeticamente fechado e termicamente isolado, com
volume de 750 , contém ar inicialmente à pressão atmosférica de 1 atm 1 atm e à
temperatura de 27C. No interior do recipiente, foi colocada uma pequena vela acesa, de
2,5 g. Sabendo‐se que a massa da vela é consumida a uma taxa de 0,1 g / min e que a
queima da vela produz energia à razão de 3,6 104 J / g, determine
a) a potência W da vela acesa;
b) a quantidade de energia E produzida pela queima completa da vela;
c) o aumento ΔT da temperatura do ar no interior do recipiente, durante a queima da
vela;
d) a pressão P do ar no interior do recipiente, logo após a queima da vela.
Note e adote:
O ar deve ser tratado como gás ideal.
O volume de 1mol de gás ideal à pressão atmosférica de 1 atm e à temperatura de 27C
é 25 .
Calor molar do ar a volume constante: Cv 30 J / mol K .
Constante universal dos gases: R 1,08 atm / mol K .
0C 273 K. 0 °C = 273 K.
Devem ser desconsideradas a capacidade térmica do recipiente e a variação da massa de
gás no seu interior devido à queima da vela.
Página 16 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
26. (Unicamp 2015)
Espelhos esféricos côncavos são comumente utilizados por
dentistas porque, dependendo da posição relativa entre objeto e imagem, eles permitem
visualizar detalhes precisos dos dentes do paciente. Na figura abaixo, pode-se observar
esquematicamente a imagem formada por um espelho côncavo. Fazendo uso de raios
notáveis, podemos dizer que a flecha que representa o objeto
a) se encontra entre F e V e aponta na direção da imagem.
b) se encontra entre F e C e aponta na direção da imagem.
c) se encontra entre F e V e aponta na direção oposta à imagem.
d) se encontra entre F e C e aponta na direção oposta à imagem.
27. (Fuvest 2015) Em uma aula de laboratório de Física, para estudar propriedades de
cargas elétricas, foi realizado um experimento em que pequenas esferas eletrizadas são
injetadas na parte superior de uma câmara, em vácuo, onde há um campo elétrico
uniforme na mesma direção e sentido da aceleração local da gravidade. Observou-se
que, com campo elétrico de módulo igual a 2 103 V / m, uma das esferas, de massa
3,2 1015 kg, permanecia com velocidade constante no interior da câmara. Essa esfera
tem
Note e adote:
- carga do elétron 1,6 1019 C
- carga do próton 1,6 1019 C
- aceleração local da gravidade 10 m / s2
a) o mesmo número de elétrons e de prótons.
b) 100 elétrons a mais que prótons.
c) 100 elétrons a menos que prótons.
Página 17 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
d) 2000 elétrons a mais que prótons.
e) 2000 elétrons a menos que prótons.
28. (Fuvest 2015)
A região entre duas placas metálicas, planas e paralelas está
esquematizada na figura abaixo. As linhas tracejadas representam o campo elétrico
uniforme existente entre as placas. A distância entre as placas é 5 mm e a diferença de
potencial entre elas é 300 V. As coordenadas dos pontos A, B e C são mostradas na
figura. Determine
a) os módulos EA , EB e EC do campo elétrico nos pontos A, B e C, respectivamente;
b) as diferenças de potencial VAB e VBC entre os pontos A e B e entre os pontos B e C,
respectivamente;
c) o trabalho τ realizado pela força elétrica sobre um elétron que se desloca do ponto C
ao ponto A.
Note e adote:
O sistema está em vácuo.
Carga do elétron 1,6 1019 C.
29. (Unicamp 2015) Quando as fontes de tensão contínua que alimentam os aparelhos
elétricos e eletrônicos são desligadas, elas levam normalmente certo tempo para atingir
a tensão de U 0 V. Um estudante interessado em estudar tal fenômeno usa um
Página 18 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
amperímetro e um relógio para acompanhar o decréscimo da corrente que circula pelo
circuito a seguir em função do tempo, após a fonte ser desligada em t 0 s. Usando os
valores de corrente e tempo medidos pelo estudante, pode-se dizer que a diferença de
potencial sobre o resistor R 0,5 kΩ para t 400 ms é igual a
a) 6 V.
b) 12 V.
c) 20 V.
d) 40 V.
30. (Unicamp 2015) Por sua baixa eficiência energética, as lâmpadas incandescentes
deixarão de ser comercializadas para uso doméstico comum no Brasil. Nessas lâmpadas,
apenas 5% da energia elétrica consumida é convertida em luz visível, sendo o restante
transformado em calor. Considerando uma lâmpada incandescente que consome 60 W
de potência elétrica, qual a energia perdida em forma de calor em uma hora de
operação?
a) 10.800 J.
b) 34.200 J.
c) 205.200 J.
d) 216.000 J.
Página 19 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
31. (Fuvest 2015) O aquecimento de um forno elétrico é baseado na conversão de
energia elétrica em energia térmica em um resistor. A resistência R do resistor desse
forno, submetido a uma diferença de potencial V constante, varia com a sua
temperatura T. Na a seguir é mostrado o gráfico da função R(T) R0 α(T T0 ), sendo
R0 o valor da resistência na temperatura T0 e α uma constante.
Ao se ligar o forno, com o resistor a 20C, a corrente é 10 A. Ao atingir a temperatura
TM , a corrente é 5 A.
Determine a
a) constante α;
b) diferença de potencial V;
c) temperatura TM ;
d) potência P dissipada no resistor na temperatura TM .
32. (Unicamp 2015)
Um desafio tecnológico atual é a produção de baterias
biocompatíveis e biodegradáveis que possam ser usadas para alimentar dispositivos
inteligentes com funções médicas. Um parâmetro importante de uma bateria
biocompatível é sua capacidade específica (C), definida como a sua carga por unidade
massa, geralmente dada em mAh / g. O gráfico abaixo mostra de maneira simplificada a
diferença de potencial de uma bateria à base de melanina em função de C.
Página 20 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) Para uma diferença de potencial de 0,4V, que corrente média a bateria de massa
m 5,0g fornece, supondo que ela se descarregue completamente em um tempo t 4h?
b) Suponha que uma bateria preparada com C 10mAh / g esteja fornecendo uma
corrente constante total i 2mA a um dispositivo. Qual é a potência elétrica fornecida ao
dispositivo nessa situação?
33. (Unicamp 2015) A figura 1 apresentada a seguir representa a potência elétrica
dissipada pelo filamento de tungstênio de uma lâmpada incandescente em função da sua
resistência elétrica. Já a figura 2 apresenta a temperatura de operação do filamento em
função de sua resistência elétrica. Se uma lâmpada em funcionamento dissipa 150 W de
potência elétrica, a temperatura do filamento da lâmpada é mais próxima de:
Página 21 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) 325 C.
b) 1.250 C.
c) 3.000 C.
d) 3.750 C.
34. (Fuvest 2015) Dispõe se de várias lâmpadas incandescentes de diferentes potências,
projetadas para serem utilizadas em 110 V de tensão. Elas foram acopladas, como nas
figuras I, II e III abaixo, e ligadas em 220 V.
Página 22 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Em quais desses circuitos, as lâmpadas
funcionarão como se estivessem
individualmente ligadas a uma fonte de tensão de 110 V ?
a) Somente em I.
b) Somente em II.
c) Somente em III.
d) Em I e III.
e) Em II e III.
35. (Fuvest 2015)
A figura acima mostra parte do teclado de um piano. Os valores das frequências das
notas sucessivas, incluindo os sustenidos, representados pelo símbolo #, obedecem a
uma progressão geométrica crescente da esquerda para a direita; a razão entre as
frequências de duas notas Dó consecutivas vale 2; a frequência da nota Lá do teclado da
Página 23 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
figura é 440 Hz. O comprimento de onda, no ar, da nota Sol indicada na figura é
próximo de
Note e adote:
- 21 12 1,059
- 1,059 2 1,12
- velocidade do som no ar 340 m / s
a) 0,56 m
b) 0,86 m
c) 1,06 m
d) 1,12 m
e) 1,45 m
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
A figura abaixo mostra, de forma simplificada, o sistema de freios a disco de um
automóvel. Ao se pressionar o pedal do freio, este empurra o êmbolo de um primeiro
pistão que, por sua vez, através do óleo do circuito hidráulico, empurra um segundo
pistão. O segundo pistão pressiona uma pastilha de freio contra um disco metálico preso
à roda, fazendo com que ela diminua sua velocidade angular.
36. (Unicamp 2015) Qual o trabalho executado pela força de atrito entre o pneu e o solo
para parar um carro de massa m 1.000 kg, inicialmente a v 72 km / h, sabendo que os
Página 24 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
pneus travam no instante da frenagem, deixando de girar, e o carro desliza durante todo
o tempo de frenagem?
a) 3,6 104 J.
b) 2,0 105 J.
c) 4,0 105 J.
d) 2,6 106 J.
37. (Unicamp 2015) Considerando o diâmetro d2 do segundo pistão duas vezes maior
que o diâmetro d1 do primeiro, qual a razão entre a força aplicada ao pedal de freio pelo
pé do motorista e a força aplicada à pastilha de freio?
a) 1 4.
b) 1 2.
c) 2.
d) 4.
38. (Fuvest 2014) A primeira medida da velocidade da luz, sem o uso de métodos
astronômicos, foi realizada por Hippolyte Fizeau, em 1849. A figura abaixo mostra um
esquema simplificado da montagem experimental por ele utilizada.
Um feixe fino de luz, emitido pela fonte F, incide no espelho plano semitransparente E1.
A luz refletida por E1 passa entre dois dentes da roda dentada R, incide
perpendicularmente no espelho plano E2 que está a uma distância L da roda, é refletida e
chega ao olho do observador. A roda é então colocada a girar em uma velocidade
angular tal que a luz que atravessa o espaço entre dois dentes da roda e é refletida pelo
Página 25 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
espelho E2, não alcance o olho do observador, por atingir o dente seguinte da roda.
Nesta condição, a roda, com N dentes, gira com velocidade angular constante e dá V
voltas por segundo.
a) Escreva a expressão literal para o intervalo de tempo Δt em que a luz se desloca da
roda até E2 e retorna à roda, em função de L e da velocidade da luz c.
b) Considerando o movimento de rotação da roda, escreva, em função de N e V, a
expressão literal para o intervalo de tempo Δt decorrido entre o instante em que a luz
passa pelo ponto central entre os dentes A e B da roda e o instante em que, depois de
refletida por E2, é bloqueada no centro do dente B.
c) Determine o valor numérico da velocidade da luz, utilizando os dados abaixo.
Note e adote:
No experimento de Fizeau, os dentes da roda estão igualmente espaçados e têm a
mesma largura dos espaços vazios;
L = 8600 m;
N = 750;
V = 12 voltas por segundo.
39. (Unicamp 2014)
O encontro das águas do Rio Negro e do Solimões, nas
proximidades de Manaus, é um dos maiores espetáculos da natureza local. As águas dos
dois rios, que formam o Rio Amazonas, correm lado a lado por vários quilômetros sem
se misturarem.
a) Um dos fatores que explicam esse fenômeno é a diferença da velocidade da água nos
dois rios, cerca de vn 2 km / h para o Negro e VS 6 km / h para o Solimões. Se uma
embarcação, navegando no Rio Negro, demora tN 2 h para fazer um percurso entre
duas cidades distantes dcidades 48 km, quanto tempo levará para percorrer a mesma
distância no Rio Solimões, também rio acima, supondo que sua velocidade com relação
à água seja a mesma nos dois rios?
Página 26 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) Considere um ponto no Rio Negro e outro no Solimões, ambos à profundidade de 5
m e em águas calmas, de forma que as águas nesses dois pontos estejam em repouso. Se
a densidade da água do Rio Negro é ρN 996 kg / m3 e a do Rio Solimões é
ρS 998 kg / m3, qual a diferença de pressão entre os dois pontos?
40. (Unicamp 2014) Correr uma maratona requer preparo físico e determinação. A uma
pessoa comum se recomenda, para o treino de um dia, repetir 8 vezes a seguinte
sequência: correr a distância de 1 km à velocidade de 10,8 km/h e, posteriormente,
andar rápido a 7,2 km/h durante dois minutos.
a) Qual será a distância total percorrida pelo atleta ao terminar o treino?
b) Para atingir a velocidade de 10,8 km/h, partindo do repouso, o atleta percorre 3 m
com aceleração constante. Calcule o módulo da aceleração a do corredor neste trecho.
41. (Fuvest 2014) Arnaldo e Batista disputam uma corrida de longa distância. O gráfico
das velocidades dos dois atletas, no primeiro minuto da corrida, é mostrado na figura.
Determine
a) a aceleração aB de Batista em t = 10 s;
b) as distâncias dA e dB percorridas por Arnaldo e Batista, respectivamente, até t = 50
s;
c) a velocidade média v A de Arnaldo no intervalo de tempo entre 0 e 50 s.
Página 27 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
42. (Unicamp 2014) As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem
substituir dezenas de trabalhadores rurais, o que pode alterar de forma significativa a
relação de trabalho nas lavouras de cana-de-açúcar. A pá cortadeira da máquina
ilustrada na figura abaixo gira em movimento circular uniforme a uma frequência de
300 rpm. A velocidade de um ponto extremo P da pá vale
(Considere π 3. )
a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
43. (Fuvest 2014) Para passar de uma margem a outra de um rio, uma pessoa se
pendura na extremidade de um cipó esticado, formando um ângulo de 30° com a
vertical, e inicia, com velocidade nula, um movimento pendular. Do outro lado do rio, a
pessoa se solta do cipó no instante em que sua velocidade fica novamente igual a zero.
Imediatamente antes de se soltar, sua aceleração tem
Note e adote:
Forças dissipativas e o tamanho da pessoa devem ser ignorados.
A aceleração da gravidade local é g = 10 m/s2.
sen 30 cos 60 0,5
cos 30 sen 60 0,9
a) valor nulo.
b) direção que forma um ângulo de 30° com a vertical e módulo 9 m/s2.
Página 28 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
c) direção que forma um ângulo de 30° com a vertical e módulo 5 m/s2.
d) direção que forma um ângulo de 60° com a vertical e módulo 9 m/s2.
e) direção que forma um ângulo de 60° com a vertical e módulo 5 m/s2.
44. (Fuvest 2014) Duas pequenas esferas, cada uma com massa de 0,2 kg, estão presas
nas extremidades de uma haste rígida, de 10 cm de comprimento, cujo ponto médio está
fixo no eixo de um motor que fornece 4 W de potência mecânica. A figura abaixo
ilustra o sistema.
No instante t = 0, o motor é ligado e o sistema, inicialmente em repouso, passa a girar
em torno do eixo. Determine
a) a energia cinética total E das esferas em t = 5 s;
b) a velocidade angular ω de cada esfera em t = 5 s;
c) a intensidade F da força entre cada esfera e a haste, em t = 5 s;
d) a aceleração angular média α de cada esfera, entre t = 0 e t = 5 s.
Note e adote:
As massas da haste e do eixo do motor devem ser
ignoradas.
Não atuam forças dissipativas no sistema.
45. (Fuvest 2014) Uma estação espacial foi projetada com formato cilíndrico, de raio R
igual a 100 m, como ilustra a figura abaixo.
Página 29 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna
da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular
constante ω. As pessoas terão sensação de peso, como se estivessem na Terra, se a
velocidade ω for de, aproximadamente,
Note e adote:
A aceleração gravitacional na superfície da Terra é g = 10 m/s2.
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
46. (Fuvest 2014) Há um ponto no segmento de reta unindo o Sol à Terra, denominado
“Ponto de Lagrange L1”. Um satélite artificial colocado nesse ponto, em órbita ao redor
do Sol, permanecerá sempre na mesma posição relativa entre o Sol e a Terra.
Nessa situação, ilustrada na figura acima, a velocidade angular orbital ωA do satélite em
torno do Sol será igual à da Terra, ωT .
Para essa condição, determine
Página 30 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) ωT
em função da constante gravitacional G, da massa MS do Sol e da distância R
entre a Terra e o Sol;
b) o valor de
ωA em rad/s;
c) a expressão do módulo Fr da força gravitacional resultante que age sobre o satélite,
em função de G, MS ,MT, m, R e d, sendo MT e m, respectivamente, as massas da Terra
e do satélite e d a distância entre a Terra e o satélite.
Note e adote:
1ano 3,14 107 s.
O módulo da força gravitacional F entre dois corpos de massas M1 e M2, sendo r a
distância entre eles, é dado por F = G M1 M2/r2.
Considere as órbitas circulares.
47. (Fuvest 2014) Um contêiner com equipamentos científicos é mantido em uma
estação de pesquisa na Antártida. Ele é feito com material de boa isolação térmica e é
possível, com um pequeno aquecedor elétrico, manter sua temperatura interna
constante, Ti 20C, quando a temperatura externa é Te 40C. As paredes, o piso e o
teto do contêiner têm a mesma espessura, ε 26 cm, e são de um mesmo material, de
condutividade térmica k 0,05 J / (s m C). Suas dimensões internas são 2 3 4 m3.
Para essas condições, determine
a) a área A da superfície interna total do contêiner;
b) a potência P do aquecedor, considerando ser ele a única fonte de calor;
c) a energia E, em kWh, consumida pelo aquecedor em um dia.
Note e adote:
A quantidade de calor por unidade de tempo (Φ) que flui através de um material de
área A, espessura ε
e condutividade térmica k, com diferença de temperatura ΔT
entre as faces do material, é dada por: Φ kAΔT / ε.
Página 31 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
48. (Fuvest 2014) No sistema cardiovascular de um ser humano, o coração funciona
como uma bomba, com potência média de 10 W, responsável pela circulação sanguínea.
Se uma pessoa fizer uma dieta alimentar de 2500 kcal diárias, a porcentagem dessa
energia utilizada para manter sua circulação sanguínea será, aproximadamente, igual a
Note e adote:
1 cal = 4 J.
a) 1%
b) 4%
c) 9%
d) 20%
e) 25%
49. (Fuvest 2014) Um corpo de massa M desliza sem atrito, sujeito a uma força
gravitacional vertical uniforme, sobre um “escorregador logarítmico”: suas coordenadas
(x, y) no plano cartesiano, que representam distâncias medidas em metros, pertencem ao
gráfico da função
f(x) log 1 x 4.
2
O corpo começa sua trajetória, em repouso, no ponto A, de abscissa x 1, e atinge o
chão no ponto B, de ordenada y 0, conforme figura abaixo.
Não levando em conta as dimensões do corpo e adotando 10m/s2 como o valor da
aceleração da gravidade,
Página 32 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) encontre a abscissa do ponto B;
b) escreva uma expressão para a energia mecânica do corpo em termos de sua massa M,
de sua altura y e de sua velocidade escalar v;
c) obtenha a velocidade escalar v como função da abscissa do ponto ocupado pelo
corpo;
d) encontre a abscissa do ponto a partir do qual v é maior do que 60 m / s.
50. (Unicamp 2014)
a) O ar atmosférico oferece uma resistência significativa ao
movimento dos automóveis. Suponha que um determinado automóvel movido a
gasolina, trafegando em linha reta a uma velocidade constante de v 72 km / h com
relação ao ar, seja submetido a uma força de atrito de Far 380 N. Em uma viagem de
uma hora, aproximadamente quantos litros de gasolina serão consumidos somente para
“vencer” o atrito imposto pelo ar?
Dados: calor de combustão da gasolina: 35 MJ/l. Rendimento do motor a gasolina:
30%.
b) A má calibração dos pneus é outro fator que gera gasto extra de combustível. Isso
porque o rolamento é real e a baixa pressão aumenta a superfície de contato entre o solo
e o pneu. Como consequência, o ponto efetivo da aplicação da força normal de módulo
N não está verticalmente abaixo do eixo de rotação da roda (ponto O) e sim ligeiramente
deslocado para a frente a uma distância d , como indica a figura abaixo.
Página 33 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
As forças que atuam sobre a roda não tracionada são: força F, que leva a roda para a
frente, força peso P, força de atrito estático Fat e força normal N. Para uma velocidade
de translação V constante, o torque em relação ao ponto O, resultante das forças de
atrito estático Fat e normal N, deve ser nulo. Sendo R = 30 cm, d = 0,3 cm e N = 2.500
N, calcule o módulo da força de atrito estático Fat .
51. (Fuvest 2014) Em uma competição de salto em distância, um atleta de 70 kg tem,
imediatamente antes do salto, uma velocidade na direção horizontal de módulo 10 m/s.
Ao saltar, o atleta usa seus músculos para empurrar o chão na direção vertical,
produzindo uma energia de 500 J, sendo 70% desse valor na forma de energia cinética.
Imediatamente após se separar do chão, o módulo da velocidade do atleta é mais
próximo de
a) 10,0 m/s
b) 10,5 m/s
c) 12,2 m/s
d) 13,2 m/s
e) 13,8 m/s
52. (Fuvest 2014) Uma pessoa faz, diariamente, uma caminhada de 6 km em uma pista
horizontal, consumindo 80 cal a cada metro. Num certo dia, ela fez sua caminhada
habitual e, além disso, subiu um morro de 300 m de altura. Essa pessoa faz uma
alimentação diária de 2000 kcal, com a qual manteria seu peso, se não fizesse
exercícios.
Com base nessas informações, determine
Página 34 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) a percentagem P da energia química proveniente dos alimentos ingeridos em um dia
por essa pessoa, equivalente à energia consumida na caminhada de 6 km;
b) a quantidade C de calorias equivalente à variação de energia potencial dessa pessoa
entre a base e o topo do morro, se sua massa for 80 kg;
c) o número N de caminhadas de 6 km que essa pessoa precisa fazer para perder 2,4 kg
de gordura, se mantiver a dieta diária de 2000 kcal.
Note e adote:
A aceleração da gravidade local é igual a 10 m/s2.
1 cal = 4 J.
9 kcal são produzidas com a queima de 1 g de
gordura.
53. (Unicamp 2014) A figura abaixo exibe, em porcentagem, a previsão da oferta de
energia no Brasil em 2030, segundo o Plano Nacional de Energia.
Página 35 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Segundo o plano, em 2030, a oferta total de energia do país irá atingir 557 milhões de
tep (toneladas equivalentes de petróleo). Nesse caso, podemos prever que a parcela
oriunda de fontes renováveis, indicada em cinza na figura, equivalerá a
a) 178,240 milhões de tep.
b) 297,995 milhões de tep.
c) 353,138 milhões de tep.
d) 259,562 milhões de tep.
54. (Unicamp 2014)
Uma boia de sinalização marítima muito simples pode ser
construída unindo-se dois cilindros de mesmas dimensões e de densidades diferentes,
sendo um de densidade menor e outro de densidade maior que a da água, tal como
esquematizado na figura abaixo. Submergindo-se totalmente esta boia de sinalização na
água, quais serão os pontos efetivos mais prováveis de aplicação das forças Peso e
Empuxo?
a) Peso em C e Empuxo em B.
b) Peso em B e Empuxo em B.
c) Peso em C e Empuxo em A.
d) Peso em B e Empuxo em C.
55. (Fuvest 2014)
Um bloco de madeira impermeável, de massa M e dimensões 2 3 3 cm3, é inserido
muito lentamente na água de um balde, até a condição de equilíbrio, com metade de seu
Página 36 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
volume submersa. A água que vaza do balde é coletada em um copo e tem massa m. A
figura ilustra as situações inicial e final; em ambos os casos, o balde encontra-se cheio
de água até sua capacidade máxima. A relação entre as massas m e M é tal que
a) m = M/3
b) m = M/2
c) m = M
d) m = 2M
e) m = 3M
56. (Unicamp 2014) Existem inúmeros tipos de extintores de incêndio que devem ser
utilizados de acordo com a classe do fogo a se extinguir. No caso de incêndio
envolvendo líquidos inflamáveis, classe B, os extintores à base de pó químico ou de
dióxido de carbono (CO2) são recomendados, enquanto extintores de água devem ser
evitados, pois podem espalhar o fogo.
a) Considere um extintor de CO2 cilíndrico de volume interno V = 1800 cm3 que contém
uma massa de CO2 m = 6 kg. Tratando o CO2 como um gás ideal, calcule a pressão no
interior do extintor para uma temperatura T = 300 K.
Dados: R = 8,3 J/mol K e a massa molar do CO2 M = 44 g/mol.
b) Suponha que um extintor de CO2 (similar ao do item a), completamente carregado,
isolado e inicialmente em repouso, lance um jato de CO2 de massa m = 50 g com
velocidade v = 20 m/s. Estime a massa total do extintor mEXT e calcule a sua
velocidade de recuo provocada pelo lançamento do gás.
Despreze a variação da massa total do cilindro decorrente do lançamento do jato.
Página 37 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
57. (Fuvest 2014) Um núcleo de polônio-204 (204Po), em repouso, transmuta-se em um
núcleo de chumbo-200 (200Pb), emitindo uma partícula alfa (α ) com energia cinética
Eα . Nesta reação, a energia cinética do núcleo de chumbo é igual a
Note e adote:
Núcleo
Massa (u)
204
Po
204
200
Pb
200
4
α
1 u = 1 unidade de massa
atômica.
a) Eα .
b) Eα / 4
c) Eα / 50
d) Eα / 200
e) Eα / 204
58. (Unicamp 2014) “As denúncias de violação de telefonemas e transmissão de dados
de empresas e cidadãos brasileiros serviram para reforçar a tese das Forças Armadas da
necessidade de o Brasil dispor de seu próprio satélite geoestacionário de comunicação
militar” (O Estado de São Paulo, 15/07/2013). Uma órbita geoestacionária é
caracterizada por estar no plano equatorial terrestre, sendo que o satélite que a executa
está sempre acima do mesmo ponto no equador da superfície terrestre. Considere que a
órbita geoestacionária tem um raio r
42000 km.
a) Calcule a aceleração centrípeta de um satélite em órbita circular geoestacionária.
b) A energia mecânica de um satélite de massa m em órbita circular em torno da terra é
dada por E
G 6,7 1011
GMm
, em que r é o raio da órbita, M 6 1024 kg é a massa da Terra e
2r
Nm2
kg2
. O raio de órbita de satélites comuns de observação (não
Página 38 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
geoestacionários) é tipicamente de 7000 km. Calcule a energia adicional necessária para
colocar um satélite de 200 kg de massa em uma órbita geoestacionária, em comparação
a colocá-lo em uma órbita comum de observação.
59. (Fuvest 2014) Uma lâmina bimetálica de bronze e ferro, na temperatura ambiente, é
fixada por uma de suas extremidades, como visto na figura abaixo.
Nessa situação, a lâmina está plana e horizontal. A seguir, ela é aquecida por uma
chama de gás. Após algum tempo de aquecimento, a forma assumida pela lâmina será
mais adequadamente representada pela figura:
Note e adote:
O coeficiente de dilatação térmica linear do ferro é 1,2 105 C1.
O coeficiente de dilatação térmica linear do bronze é 1,8 105 C1.
Após o aquecimento, a temperatura da lâmina é uniforme.
a)
b)
c)
d)
e)
60. (Unicamp 2014) a) Segundo as especificações de um fabricante, um forno de
micro-ondas necessita, para funcionar, de uma potência de entrada de P = 1400 W, dos
quais 50% são totalmente utilizados no aquecimento dos alimentos. Calcule o tempo
Página 39 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
necessário para elevar em Δθ 20 C a temperatura de m = 100 g de água. O calor
específico da água é ca 4,2 J / gC.
b) A figura abaixo mostra o esquema de um forno de micro-ondas, com 30 cm de
distância entre duas de suas paredes internas paralelas, assim como uma representação
simplificada de certo padrão de ondas estacionárias em seu interior. Considere a
velocidade das ondas no interior do forno como c 3 108 m / s e calcule a frequência f
das ondas que formam o padrão representado na figura.
61. (Unicamp 2014) O sistema de imagens street view disponível na internet permite a
visualização de vários lugares do mundo através de fotografias de alta definição,
tomadas em 360 graus, no nível da rua.
a) Em uma câmera fotográfica tradicional, como a representada na figura abaixo, a
imagem é gravada em um filme fotográfico para posterior revelação. A posição da lente
é ajustada de modo a produzir a imagem no filme colocado na parte posterior da
câmera. Considere uma câmera para a qual um objeto muito distante fornece uma
imagem pontual no filme em uma posição p’ = 5 cm. O objeto é então colocado mais
perto da câmera, em uma posição p = 100 cm, e a distância entre a lente e o filme é
ajustada até que uma imagem nítida real invertida se forme no filme, conforme mostra a
figura. Obtenha a variação da posição da imagem p’ decorrente da troca de posição do
objeto.
b) Nas câmeras fotográficas modernas, a captação da imagem é feita normalmente por
um sensor tipo CCD (Charge Couple Devide). Esse tipo de dispositivo possui trilhas de
capacitores que acumulam cargas elétricas proporcionalmente à intensidade da luz
Página 40 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
incidente em cada parte da trilha. Considere um conjunto de 3 capacitores de mesma
capacitância C = 0,6 pF, ligados em série conforme a figura ao lado. Se o conjunto de
capacitores é submetido a uma diferença de potencial V = 5,0 V, qual é a carga elétrica
total acumulada no conjunto?
62. (Fuvest 2014) Um estudante construiu um microscópio ótico digital usando uma
webcam, da qual ele removeu a lente original. Ele preparou um tubo adaptador e fixou
uma lente convergente, de distância focal f = 50 mm, a uma distância d = 175 mm do
sensor de imagem da webcam, como visto na figura abaixo.
No manual da webcam, ele descobriu que seu sensor de imagem tem dimensão total útil
de 6 6 mm2, com 500 500 pixels. Com estas informações, determine
a) as dimensões do espaço ocupado por cada pixel;
b) a distância L entre a lente e um objeto, para que este fique focalizado no sensor;
c) o diâmetro máximo D que uma pequena esfera pode ter, para que esteja integralmente
dentro do campo visual do microscópio, quando focalizada.
Note e adote:
Página 41 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Pixel é a menor componente de uma imagem digital.
Para todos os cálculos, desconsidere a espessura da
lente.
63. (Unicamp 2014) A atração e a repulsão entre partículas carregadas têm inúmeras
aplicações industriais, tal como a pintura eletrostática. As figuras abaixo mostram um
mesmo conjunto de partículas carregadas, nos vértices de um quadrado de lado a, que
exercem forças eletrostáticas sobre a carga A no centro desse quadrado. Na situação
apresentada, o vetor que melhor representa a força resultante agindo sobre a carga A se
encontra na figura
a)
b)
c)
d)
64. (Fuvest 2014) Dois fios metálicos, F1 e F2, cilíndricos, do mesmo material de
resistividade ρ, de seções transversais de áreas, respectivamente, A1 e A2 = 2A1, têm
Página 42 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
comprimento L e são emendados, como ilustra a figura abaixo. O sistema formado pelos
fios é conectado a uma bateria de tensão V.
Nessas condições, a diferença de potencial V1, entre as extremidades de F1, e V2, entre
as de F2, são tais que
a) V1 = V2/4
b) V1 = V2/2
c) V1 = V2
d) V1 = 2V2
e) V1 = 4V2
65. (Unicamp 2014) No fenômeno de “Magneto impedância gigante”, a resistência
elétrica de determinado material pelo qual circula uma corrente alternada de frequência f
varia com a aplicação de um campo magnético H . O gráfico da figura 1 mostra a
resistência elétrica de determinado fio de resistividade elétrica
ρ 64,8 108 Ωm em função da frequência f da corrente elétrica alternada que circula
por esse fio, para diferentes valores de H .
a) Como podemos ver na figura 1, o valor da resistência elétrica do fio para f 0 Hz é
R 1,5Ω. Calcule o comprimento L desse fio, cuja área de seção transversal vale
A 1,296 108 m2.
b) Para altas frequências, a corrente elétrica alternada não está uniformemente
distribuída na seção reta do fio, mas sim confinada em uma região próxima a sua
superfície. Esta região é determinada pelo comprimento de penetração, que é dado por
δk
ρ
, em que ρ
μr f
é a resistividade do fio, f é a frequência da corrente elétrica
Página 43 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
alternada, μ r
que μ r
é a permeabilidade magnética relativa do fio e k 500
m Hz
. Sabendo
Ω
varia com o campo magnético aplicado H , como mostra a figura 2, e que, para
o particular valor de f 8 MHz temos R 4 Ω, calcule o valor de δ
para essa situação.
66. (Fuvest 2014) A curva característica de uma lâmpada do tipo led (diodo emissor de
luz) é mostrada no gráfico.
Essa lâmpada e um resistor de resistência R estão ligados em série a uma bateria de 4,5
V, como representado na figura abaixo.
Página 44 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Nessa condição, a tensão na lâmpada é 2,5 V.
a) Qual é o valor da corrente iR no resistor?
b) Determine o valor da resistência R.
c) A bateria de 4,5 V é substituída por outra de 3 V, que fornece 60 mW de potência ao
circuito, sem que sejam trocados a lâmpada e o resistor. Nessas condições, qual é a
potência PR dissipada no resistor?
Note e adote:
As resistências internas das baterias devem ser
ignoradas.
67. (Fuvest 2014) Partículas com carga elétrica positiva penetram em uma câmara em
vácuo, onde há, em todo seu interior, um campo elétrico de módulo E e um campo
magnético de módulo B, ambos uniformes e constantes, perpendiculares entre si, nas
direções e sentidos indicados na figura. As partículas entram na câmara com
velocidades perpendiculares aos campos e de módulos v1 (grupo 1), v2 (grupo 2) e v3
(grupo 3). As partículas do grupo 1 têm sua trajetória encurvada em um sentido, as do
grupo 2, em sentido oposto, e as do grupo 3 não têm sua trajetória desviada. A situação
está ilustrada na figura abaixo.
Considere as seguintes afirmações sobre as velocidades das partículas de cada grupo:
I. v1 > v2 e v1 > E/B
II. v1 < v2 e v1 < E/B
III. v3 = E/B
Página 45 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Está correto apenas o que se afirma em
Note e adote:
Os módulos das forças elétrica (FE) e magnética (FM) são:
FE = qE
FM = qvB
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
68. (Fuvest 2014) O resultado do exame de audiometria de uma pessoa é mostrado nas
figuras abaixo. Os gráficos representam o nível de intensidade sonora mínima I, em
decibéis (dB), audível por suas orelhas direita e esquerda, em função da frequência f do
som, em kHz. A comparação desse resultado com o de exames anteriores mostrou que,
com o passar dos anos, ela teve perda auditiva. Com base nessas informações, foram
feitas as seguintes afirmações sobre a audição dessa pessoa:
I. Ela ouve sons de frequência de 6 kHz e intensidade de 20 dB com a orelha direita,
mas não com a esquerda.
II. Um sussurro de 15 dB e frequência de 0,25 kHz é ouvido por ambas as orelhas.
III. A diminuição de sua sensibilidade auditiva, com o passar do tempo, pode ser
atribuída a degenerações dos ossos martelo, bigorna e estribo, da orelha externa, onde
ocorre a conversão do som em impulsos elétricos.
Página 46 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
É correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
69. (Unicamp 2014) A tecnologia de telefonia celular 4G passou a ser utilizada no
Brasil em 2013, como parte da iniciativa de melhoria geral dos serviços no Brasil, em
preparação para a Copa do Mundo de 2014. Algumas operadoras inauguraram serviços
com ondas eletromagnéticas na frequência de 40 MHz. Sendo a velocidade da luz no
vácuo c 3,0 108 m / s, o comprimento de onda dessas ondas eletromagnéticas é
a) 1,2 m.
b) 7,5 m.
c) 5,0 m.
d) 12,0 m.
70. (Fuvest 2014) O Sr. Rubinato, um músico aposentado, gosta de ouvir seus velhos
discos sentado em uma poltrona. Está ouvindo um conhecido solo de violino quando
sua esposa Matilde afasta a caixa acústica da direita (Cd) de uma distância l, como visto
na figura abaixo.
Página 47 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Em seguida, Sr. Rubinato reclama: _ Não consigo mais ouvir o Lá do violino, que antes
soava bastante forte! Dentre as alternativas abaixo para a distância l, a única compatível
com a reclamação do Sr. Rubinato é
Note e adote:
O mesmo sinal elétrico do amplificador é ligado aos dois alto-falantes, cujos cones se
movimentam em fase.
A frequência da nota Lá é 440 Hz.
A velocidade do som no ar é 330 m/s.
A distância entre as orelhas do Sr. Rubinato deve ser ignorada.
a) 38 cm
b) 44 cm
c) 60 cm
d) 75 cm
e) 150 cm
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Leia o texto:
Andar de bondinho no complexo do Pão de Açúcar no Rio de Janeiro é um dos passeios
aéreos urbanos mais famosos do mundo. Marca registrada da cidade, o Morro do Pão de
Açúcar é constituído de um único bloco de granito, despido de vegetação em sua quase
totalidade e tem mais de 600 milhões de anos.
Página 48 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
71. (Unicamp 2014) O passeio completo no complexo do Pão de Açúcar inclui um
trecho de bondinho de aproximadamente 540 m, da Praia Vermelha ao Morro da Urca,
uma caminhada até a segunda estação no Morro da Urca, e um segundo trecho de
bondinho de cerca de 720 m, do Morro da Urca ao Pão de Açúcar. A velocidade escalar
média do bondinho no primeiro trecho é v1 10,8 km / h e, no segundo, é
v 2 14,4 km / h. Supondo que, em certo dia, o tempo gasto na caminhada no Morro da
Urca somado ao tempo de espera nas estações é de 30 minutos, o tempo total do passeio
completo da Praia Vermelha até o Pão de Açúcar será igual a
a) 33 min.
b) 36 min.
c) 42 min.
d) 50 min.
72. (Unicamp 2014) A altura do Morro da Urca é de 220 m e a altura do Pão de Açúcar
é de cerca de 400 m, ambas em relação ao solo. A variação da energia potencial
gravitacional do bondinho com passageiros de massa total M = 5000 kg, no segundo
trecho do passeio, é
(Use g 10 m / s2. )
a) 11 106 J.
b) 20 106 J.
c) 31 106 J.
d) 9 106 J.
73. (Fuvest 2013) Antes do início dos Jogos Olímpicos de 2012, que aconteceram em
Londres, a chama olímpica percorreu todo o Reino Unido, pelas mãos de cerca de 8000
pessoas, que se revezaram nessa tarefa. Cada pessoa correu durante um determinado
tempo e transferiu a chama de sua tocha para a do próximo participante.
Suponha que
(i) cada pessoa tenha recebido uma tocha contendo cerca de 1,02 g de uma mistura de
butano e propano, em igual proporção, em mols;
(ii) a vazão de gás de cada tocha fosse de 48 mL/minuto.
Página 49 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Calcule:
a) a quantidade de matéria, em mols, da mistura butano+propano contida em cada tocha;
b) o tempo durante o qual a chama de cada tocha podia ficar acesa.
Um determinado participante P do revezamento correu a uma velocidade média de 2,5
m/s. Sua tocha se apagou no exato instante em que a chama foi transferida para a tocha
do participante que o sucedeu.
c) Calcule a distância, em metros, percorrida pelo participante P enquanto a chama de
sua tocha permaneceu acesa.
Dados: Massa molar (g/mol): butano = 58, propano = 44; Volume molar nas condições
ambientes: 24 L/mol.
74. (Unicamp 2013) O prêmio Nobel de Física de 2011 foi concedido a três astrônomos
que verificaram a expansão acelerada do universo a partir da observação de supernovas
distantes. A velocidade da luz é c = 3 108 m/s.
a) Observações anteriores sobre a expansão do universo mostraram uma relação direta
entre a velocidade v de afastamento de uma galáxia e a distância r em que ela se
encontra da Terra, dada por v = H r, em que H = 2,3 10–18 s–1 é a constante de Hubble.
Em muitos casos, a velocidade v da galáxia pode ser obtida pela expressão v
c λ
, em
λ0
que λ 0 é o comprimento de onda da luz emitida e λ é o deslocamento Doppler da luz.
Considerando ambas as expressões acima, calcule a que distância da Terra se encontra
uma galáxia, se λ 0,092 λ0 .
b) Uma supernova, ao explodir, libera para o espaço massa em forma de energia, de
acordo com a expressão E = mc2. Numa explosão de supernova foram liberados 3,24
1048 J, de forma que sua massa foi reduzida para mfinal = 4,0 1030 kg. Qual era a massa
da estrela antes da explosão?
75. (Unicamp 2013) Alguns tênis esportivos modernos possuem um sensor na sola que
permite o monitoramento do desempenho do usuário durante as corridas. O
Página 50 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
monitoramento pode ser feito através de relógios ou telefones celulares que recebem as
informações do sensor durante os exercícios. Considere um atleta de massa m = 70 kg
que usa um tênis com sensor durante uma série de três corridas.
a) O gráfico 1) abaixo mostra a distância percorrida pelo atleta e a duração em horas das
três corridas realizadas em velocidades constantes distintas. Considere que, para essa
série de corridas, o consumo de energia do corredor pode ser aproximado por
E CMET m t , onde m é a massa do corredor, t é a duração da corrida e CMET é uma
kJ
constante que depende da velocidade do corredor e é expressa em unidade de
.
kg h
Usando o gráfico 2) abaixo, que expressa CMET em função da velocidade do corredor,
calcule a quantidade de energia que o atleta gastou na terceira corrida.
b) O sensor detecta o contato da sola do tênis com o solo pela variação da pressão.
Estime a área de contato entre o tênis e o solo e calcule a pressão aplicada no solo
quando o atleta está em repouso e apoiado sobre um único pé.
76. (Unicamp 2013) Em 2012 foi comemorado o centenário da descoberta dos raios
cósmicos, que são partículas provenientes do espaço.
a) Os neutrinos são partículas que atingem a Terra, provenientes em sua maioria do Sol.
Sabendo-se que a distância do Sol à Terra é igual a 1,5 1011 m , e considerando a
velocidade dos neutrinos igual a 3,0 108 m/s , calcule o tempo de viagem de um
neutrino solar até a Terra.
Página 51 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) As partículas ionizam o ar e um instrumento usado para medir esta ionização é o
eletroscópio. Ele consiste em duas hastes metálicas que se repelem quando carregadas.
De forma simplificada, as hastes podem ser tratadas como dois pêndulos simples de
mesma massa m e mesma carga q localizadas nas suas extremidades. O módulo da força
elétrica entre as cargas é dado por Fe k
q2
d2
9
2
2
, sendo k = 9 10 N m /C . Para a situação
ilustrada na figura abaixo, qual é a carga q, se m = 0,004 g?
77. (Unicamp 2013) Para fins de registros de recordes mundiais, nas provas de 100
metros rasos não são consideradas as marcas em competições em que houver vento
favorável (mesmo sentido do corredor) com velocidade superior a 2 m s. Sabe-se que,
com vento favorável de 2 m s, o tempo necessário para a conclusão da prova é reduzido
em 0,1s. Se um velocista realiza a prova em 10 s sem vento, qual seria sua velocidade
se o vento fosse favorável com velocidade de 2 m s?
a) 8,0 m/s.
b) 9,9 m/s.
c) 10,1 m/s.
d) 12,0 m/s.
78. (Fuvest 2013) Um DJ, ao preparar seu equipamento, esquece uma caixa de fósforos
sobre o disco de vinil, em um toca-discos desligado. A caixa se encontra a 10 cm do
centro do disco. Quando o toca-discos é ligado, no instante t 0, ele passa a girar com
aceleração angular constante α 1,1rad/s2, até que o disco atinja a frequência final
f 33 rpm que permanece constante. O coeficiente de atrito estático entre a caixa de
fósforos e o disco é μe 0,09. Determine
Página 52 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) a velocidade angular final do disco, ωf , em rad/s;
b) o instante tf em que o disco atinge a velocidade angular ωf ;
c) a velocidade angular ωc do disco no instante tc em que a caixa de fósforos passa a se
deslocar em relação ao mesmo;
d) o ângulo total θ percorrido pela caixa de fósforos desde o instante t 0 até o
instante t tc .
Note e adote: Aceleração da gravidade local g 10 m/s2; π 3.
79. (Unicamp 2013) Em agosto de 2012, a NASA anunciou o pouso da sonda Curiosity
na superfície de Marte. A sonda, de massa m = 1000 kg, entrou na atmosfera marciana a
uma velocidade v0 = 6000 m/s.
a) A sonda atingiu o repouso, na superfície de Marte, 7 minutos após a sua entrada na
atmosfera. Calcule o módulo da força resultante média de desaceleração da sonda
durante sua descida.
b) Considere que, após a entrada na atmosfera a uma altitude h0 = 125 km, a força de
atrito reduziu a velocidade da sonda para v = 4000 m/s quando a altitude atingiu h =100
km. A partir da variação da energia mecânica, calcule o trabalho realizado pela força de
atrito neste trecho. Considere a aceleração da gravidade de Marte, neste trecho,
constante e igual a gMarte = 4 m/s2.
80. (Unicamp 2013) As nuvens são formadas por gotículas de água que são facilmente
arrastadas pelo vento. Em determinadas situações, várias gotículas se juntam para
formar uma gota maior, que cai, produzindo a chuva. De forma simplificada, a queda da
gota ocorre quando a força gravitacional que age sobre ela fica maior que a força do
vento ascendente. A densidade da água é ρágua 1,0 103 kg/m3 .
a) O módulo da força, que é vertical e para cima, que certo vento aplica sobre uma gota
esférica de raio r pode ser aproximado por Fvento b r , com b 1,6 103 N/m. Calcule o
raio mínimo da gota para que ela comece a cair.
Página 53 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) O volume de chuva e a velocidade com que as gotas atingem o solo são fatores
importantes na erosão. O volume é usualmente expresso pelo índice pluviométrico, que
corresponde à altura do nível da água da chuva acumulada em um recipiente aberto e
disposto horizontalmente. Calcule o impulso transferido pelas gotas da chuva para cada
metro quadrado de solo horizontal, se a velocidade média das gotas ao chegar ao solo é
de 2,5 m/s e o índice pluviométrico é igual a 20 mm. Considere a colisão como
perfeitamente inelástica.
81. (Fuvest 2013) O pêndulo de um relógio é constituído por uma haste rígida com um
disco de metal preso em uma de suas extremidades. O disco oscila entre as posições A e
C, enquanto a outra extremidade da haste permanece imóvel no ponto P. A figura
abaixo ilustra o sistema. A força resultante que atua no disco quando ele passa por B,
com a haste na direção vertical, é
(Note e adote: g é a aceleração local da gravidade.)
a) nula.
b) vertical, com sentido para cima.
c) vertical, com sentido para baixo.
d) horizontal, com sentido para a direita.
e) horizontal, com sentido para a esquerda.
82. (Fuvest 2013) A potência elétrica instalada no Brasil é 100 GW. Considerando que
o equivalente energético do petróleo seja igual a 4 107 J/L, que a potência média de
radiação solar por unidade de área incidente na superfície terrestre seja igual a 250
W/m2 e que a relação de equivalência entre massa m e energia E é expressa por E mc2,
determine
Página 54 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) a área A de superfície terrestre, na qual incide uma potência média de radiação solar
equivalente à potência elétrica instalada no Brasil;
b) a energia elétrica EB consumida no Brasil em um ano, supondo que, em média, 80%
da potência instalada seja utilizada;
c) o volume V de petróleo equivalente à energia elétrica consumida no Brasil em um
ano;
d) a massa m equivalente à energia elétrica consumida no Brasil em um ano.
Note e adote: 1GW 109 W; c 3 108 m/s; 1 ano = 3 107 s.
83. (Unicamp 2013) Um aerogerador, que converte energia eólica em elétrica, tem uma
hélice como a representada na figura abaixo. A massa do sistema que gira é M 50
toneladas, e a distância do eixo ao ponto P, chamada de raio de giração, é R 10 m. A
1
2
energia cinética do gerador com a hélice em movimento é dada por E MVP2 , sendo
VP o módulo da velocidade do ponto P. Se o período de rotação da hélice é igual a 2 s,
qual é a energia cinética do gerador? Considere π 3.
a) 6,250 105 J.
b) 2,250 107 J.
c) 5,625 107 J.
d) 9,000 107 J.
84. (Unicamp 2013)
Muitos carros possuem um sistema de segurança para os
passageiros chamado airbag. Este sistema consiste em uma bolsa de plástico que é
Página 55 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
rapidamente inflada quando o carro sofre uma desaceleração brusca, interpondo-se entre
o passageiro e o painel do veículo. Em uma colisão, a função do airbag é
a) aumentar o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo
assim a força recebida pelo passageiro.
b) aumentar a variação de momento linear do passageiro durante a colisão, reduzindo
assim a força recebida pelo passageiro.
c) diminuir o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo
assim a força recebida pelo passageiro.
d) diminuir o impulso recebido pelo passageiro devido ao choque, reduzindo assim a
força recebida pelo passageiro.
85. (Fuvest 2013) Compare as colisões de uma bola de vôlei e de uma bola de golfe
com o tórax de uma pessoa, parada e em pé. A bola de vôlei, com massa de 270 g, tem
velocidade de 30 m/s quando atinge a pessoa, e a de golfe, com 45 g, tem velocidade de
60 m/s ao atingir a mesma pessoa, nas mesmas condições. Considere ambas as colisões
totalmente inelásticas. É correto apenas o que se afirma em:
(Note e adote: a massa da pessoa é muito maior que a massa das bolas; as colisões são
frontais; o tempo de interação da bola de vôlei com o tórax da pessoa é o dobro do
tempo de interação da bola de golfe; a área média de contato da bola de vôlei com o
tórax é 10 vezes maior que a área média de contato da bola de golfe.)
a) Antes das colisões, a quantidade de movimento da bola de golfe é maior que a da
bola de vôlei.
b) Antes das colisões, a energia cinética da bola de golfe é maior que a da bola de vôlei.
c) Após as colisões, a velocidade da bola de golfe é maior que a da bola de vôlei.
d) Durante as colisões, a força média exercida pela bola de golfe sobre o tórax da pessoa
é maior que a exercida pela bola de vôlei.
e) Durante as colisões, a pressão média exercida pela bola de golfe sobre o tórax da
pessoa é maior que a exercida pela bola de vôlei.
86. (Fuvest 2013) Um fóton, com quantidade de movimento na direção e sentido do
eixo x, colide com um elétron em repouso. Depois da colisão, o elétron passa a se mover
com quantidade de movimento pe , no plano xy, como ilustra a figura abaixo.
Página 56 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Dos vetores pf abaixo, o único que poderia representar a direção e sentido da
quantidade de movimento do fóton, após a colisão, é
(Note e adote: O princípio da conservação da quantidade de movimento é válido
também para a interação entre fótons e elétrons.)
a)
b)
c)
d)
e)
87. (Fuvest 2013) Uma das hipóteses para explicar a extinção dos dinossauros, ocorrida
há cerca de 60 milhões de anos, foi a colisão de um grande meteoro com a Terra.
Estimativas indicam que o meteoro tinha massa igual a 1016 kg e velocidade de 30 km/s,
imediatamente antes da colisão. Supondo que esse meteoro estivesse se aproximando da
Página 57 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Terra, numa direção radial em relação à orbita desse planeta em torno do Sol, para uma
colisão frontal, determine
a) a quantidade de movimento Pi do meteoro imediatamente antes da colisão;
b) a energia cinética Ec do meteoro imediatamente antes da colisão;
c) a componente radial da velocidade da Terra, Vr, pouco depois da colisão;
d) a energia Ed, em megatons, dissipada na colisão.
Note e adote: A órbita da Terra é circular; Massa da Terra = 6 1024 kg; 1 megaton =
4 1015 J é a energia liberada pela explosão de um milhão de toneladas de
trinitrotolueno.
88. (Unicamp 2013) A boa ventilação em ambientes fechados é um fator importante
para o conforto térmico em regiões de clima quente. Uma chaminé solar pode ser usada
para aumentar a ventilação de um edifício. Ela faz uso da energia solar para aquecer o ar
de sua parte superior, tornando-o menos denso e fazendo com que ele suba, aspirando
assim o ar dos ambientes e substituindo-o por ar vindo do exterior.
a) A intensidade da radiação solar absorvida por uma placa usada para aquecer o ar é
igual a 400 W/m2. A energia absorvida durante 1,0 min por uma placa de 2 m2 é usada
para aquecer 6,0 kg de ar. O calor específico do ar é c 1000
J
. Qual é a variação de
kg C
temperatura do ar nesse período?
b) A densidade do ar a 290 K é ρ 1,2 kg/m3. Adotando-se um número fixo de moles de
ar mantido a pressão constante, calcule a sua densidade para a temperatura de 300 K.
Considere o ar como um gás ideal.
89. (Unicamp 2013) Pressão parcial é a pressão que um gás pertencente a uma mistura
teria se o mesmo gás ocupasse sozinho todo o volume disponível. Na temperatura
ambiente, quando a umidade relativa do ar é de 100%, a pressão parcial de vapor de
água vale 3,0 103 Pa. Nesta situação, qual seria a porcentagem de moléculas de água no
ar?
Dados: a pressão atmosférica vale 1,0 105 Pa; considere que o ar se comporta como um
gás ideal.
Página 58 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) 100%.
b) 97%.
c) 33%.
d) 3%.
90. (Fuvest 2013)
Em um recipiente termicamente isolado e mantido a pressão
constante, são colocados 138 g de etanol líquido. A seguir, o etanol é aquecido e sua
temperatura T é medida como função da quantidade de calor Q a ele transferida. A partir
do gráfico de TxQ, apresentado na figura abaixo, pode-se determinar o calor específico
molar para o estado líquido e o calor latente molar de vaporização do etanol como
sendo, respectivamente, próximos de
Dados: Fórmula do etanol = C2H5OH; Massas molares = C(12g/mol), H(1g/mol),
O(16g/mol).
a) 0,12 kJ/(mol°C) e 36 kJ/mol.
b) 0,12 kJ/(mol°C) e 48 kJ/mol.
c) 0,21 kJ/(mol°C) e 36 kJ/mol.
d) 0,21 kJ/(mol°C) e 48 kJ/mol.
e) 0,35 kJ/(mol°C) e 110 kJ/mol.
91. (Fuvest 2013) O telêmetro de superposição é um instrumento ótico, de concepção
simples, que no passado foi muito utilizado em câmeras fotográficas e em aparelhos de
medição de distâncias. Uma representação esquemática de um desses instrumentos está
abaixo. O espelho semitransparente E1 está posicionado a 45° em relação à linha de
Página 59 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
visão, horizontal, AB. O espelho E2 pode ser girado, com precisão, em torno de um eixo
perpendicular à figura, passando por C, variando-se assim o ângulo β entre o plano de
E2 e a linha horizontal. Deseja-se determinar a distância AB do objeto que está no ponto
B ao instrumento.
a) Desenhe na figura abaixo, com linhas cheias, os raios de luz que, partindo do objeto
que está em B, atingem o olho do observador – um atravessa o espelho E1 e o outro é
refletido por E2 no ponto C. Suponha que ambos cheguem ao olho do observador
paralelos e superpostos.
b) Desenhe, com linhas tracejadas, o trajeto aproximado de um raio de luz que parte
do objeto em B’, incide em C e é refletido por E2.
Com o objeto em um ponto B específico, o ângulo β foi ajustado em 44°, para que os
raios cheguem ao olho do observador paralelos e superpostos. Nessa condição,
c) determine o valor do ângulo γ entre as linhas AB e BC;
d) com AC 10 cm, determine o valor de AB.
Note
e
adote:
sen(22°)=0,37;
cos(22°)=0,93;
sen(44°)=0,70;
cos(44°)=0,72;
sen(88°)=0,99; cos(88°)=0,03; As direções AB e AC são perpendiculares entre si.
92. (Unicamp 2013) O efeito de imagem tridimensional no cinema e nos televisores 3D
é obtido quando se expõe cada olho a uma mesma imagem em duas posições
ligeiramente diferentes. Um modo de se conseguir imagens distintas em cada olho é
através do uso de óculos com filtros polarizadores.
Página 60 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) Quando a luz é polarizada, as direções dos campos elétricos e magnéticos são bem
definidas. A intensidade da luz polarizada que atravessa um filtro polarizador é dada por
I I0cos2θ, onde I0 é a intensidade da luz incidente e θ é o ângulo entre o campo
elétrico E e a direção de polarização do filtro. A intensidade luminosa, a uma distância
d de uma fonte que emite luz polarizada, é dada por I0
P0
4πd 2
, em que P0 é a potência
da fonte. Sendo P0 = 24 W, calcule a intensidade luminosa que atravessa um polarizador
que se encontra a d = 2 m da fonte e para o qual θ 60.
b) Uma maneira de polarizar a luz é por reflexão. Quando uma luz não polarizada incide
na interface entre dois meios de índices de refração diferentes com o ângulo de
incidência θB , conhecido como ângulo de Brewster, a luz refletida é polarizada, como
mostra a figura abaixo. Nessas condições, θB θr 90, em que θr é o ângulo do raio
refratado. Sendo n1 = 1,0 o índice de refração do meio 1 e θB 60, calcule o índice de
refração do meio 2.
93. (Unicamp 2013)
Um objeto é disposto em frente a uma lente convergente,
conforme a figura abaixo. Os focos principais da lente são indicados com a letra F.
Pode-se afirmar que a imagem formada pela lente
Página 61 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) é real, invertida e mede 4 cm.
b) é virtual, direta e fica a 6 cm da lente.
c) é real, direta e mede 2 cm.
d) é real, invertida e fica a 3 cm da lente.
94. (Fuvest 2013) A extremidade de uma fibra ótica adquire o formato arredondado de
uma microlente ao ser aquecida por um laser, acima da temperatura de fusão. A figura
abaixo ilustra o formato da microlente para tempos de aquecimento crescentes
(t1<t2<t3).
Considere as afirmações:
I. O raio de curvatura da microlente aumenta com tempos crescentes de aquecimento.
II. A distância focal da microlente diminui com tempos crescentes de aquecimento.
III. Para os tempos de aquecimento apresentados na figura, a microlente é convergente.
Está correto apenas o que se afirma em
(Note e adote: a luz se propaga no interior da fibra ótica, da esquerda para a direita,
paralelamente ao seu eixo; a fibra está imersa no ar e o índice de refração do seu
material é 1,5.)
Página 62 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
95. (Fuvest 2013) A energia potencial elétrica U de duas partículas em função da
distância r que as separa está representada no gráfico da figura abaixo.
Uma das partículas está fixa em uma posição, enquanto a outra se move apenas devido à
força elétrica de interação entre elas. Quando a distância entre as partículas varia de
ri 3 1010 m a rf 9 1010 m, a energia cinética da partícula em movimento
a) diminui 1 1018 J.
b) aumenta 1 1018 J.
c) diminui 2 1018 J.
d) aumenta 2 1018 J.
e) não se altera.
96. (Unicamp 2013) O carro elétrico é uma alternativa aos veículos com motor a
combustão interna. Qual é a autonomia de um carro elétrico que se desloca a 60 km h,
se a corrente elétrica empregada nesta velocidade é igual a 50 A e a carga máxima
armazenada em suas baterias é q 75 Ah?
a) 40,0 km.
Página 63 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) 62,5 km.
c) 90,0 km.
d) 160,0 km.
97. (Fuvest 2013) No circuito da figura abaixo, a diferença de potencial, em módulo,
entre os pontos A e B é de
a) 5 V.
b) 4 V.
c) 3 V.
d) 1 V.
e) 0 V.
98. (Fuvest 2013)
Em uma aula de laboratório, os alunos determinaram a força
eletromotriz هe a resistência interna r de uma bateria. Para realizar a tarefa, montaram
o circuito representado na figura abaixo e, utilizando o voltímetro, mediram a diferença
de potencial V para diferentes valores da resistência R do reostato. A partir dos
resultados obtidos, calcularam a corrente I no reostato e construíram a tabela
apresentada logo abaixo.
Página 64 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
a) Complete a tabela abaixo com os valores da corrente I.
V(V) R( ) I(A)
1,14
7,55
1,10
4,40
1,05
2,62
0,96
1,60
0,85
0,94
0,15
0,40
0,90
b) Utilizando os eixos abaixo, faça o gráfico de V em função de I.
c) Determine a força eletromotriz ε e a resistência interna r da bateria.
Note e adote: Um reostato é um resistor de resistência variável; Ignore efeitos resistivos
dos fios de ligação do circuito.
99. (Unicamp 2013) Uma forma alternativa de transmissão de energia elétrica a grandes
distâncias (das unidades geradoras até os centros urbanos) consiste na utilização de
Página 65 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
linhas de transmissão de extensão aproximadamente igual a meio comprimento de onda
da corrente alternada transmitida. Este comprimento de onda é muito próximo do
comprimento de uma onda eletromagnética que viaja no ar com a mesma frequência da
corrente alternada.
a) Qual é o comprimento de onda de uma onda eletromagnética que viaja no ar com
uma frequência igual a 60 Hz? A velocidade da luz no ar é c = 3 108 m/s.
b) Se a tensão na linha é de 500 kV e a potência transmitida é de 400 MW, qual é a
corrente na linha?
100. (Fuvest 2013) Um raio proveniente de uma nuvem transportou para o solo uma
carga de 10 C sob uma diferença de potencial de 100 milhões de volts. A energia
liberada por esse raio é
(Note e adote: 1J 3 107 kWh. )
a) 30 MWh.
b) 3 MWh.
c) 300 kWh.
d) 30 kWh.
e) 3 kWh.
Página 66 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Gabarito:
Resposta
da
questão
1:
[Resposta do ponto de vista da disciplina de Biologia]
a) No vaso 1, a planta cresce normalmente, pois consegue absorver os comprimentos de
onda equivalentes ao azul e ao vermelho. Esses comprimentos de onda tornam a taxa de
fotossíntese mais eficiente. A planta do vaso 2 reflete a radiação verde e não consegue
crescer devido à ineficiência de sua taxa fotossintética.
[Resposta do ponto de vista da disciplina de Física]
b) A cor de um objeto é a mesma cor da radiação que ele mais difunde (reflete).
Portanto, se as pessoas com visão normal enxergam as folhas como verdes, é porque
elas refletem com maior intensidade a radiação correspondente à luz verde.
Resposta
da
questão
2:
[B]
Resposta de Biologia: Em um ambiente de penumbra, ao focalizar um objeto próximo,
a íris do olho relaxa, aumentando o diâmetro da pupila. Os músculos ciliares que
prendem o cristalino se contraem, causando o aumento do poder refrativo da lente do
olho.
Resposta de Física: Da maneira como a questão está, não tem resposta. Do ponto de
vista físico, a segunda afirmativa está errada em todas as opções.
Quando o indivíduo passa para um ambiente de penumbra, a íris diminui, aumentando a
abertura da pupila para que os olhos recebam maior luminosidade. Correto. Porém, para
focalizar um objeto mais próximo, os músculos ciliares se contraem, aumentando a
curvatura do cristalino, diminuindo a sua distância focal para que a imagem caia na
retina. Não ocorre variação alguma no poder refrativo do cristalino. Para mudar o
poder refrativo de um sistema óptico é necessário que se mude a substância ou
material que o constitui.
Página 67 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
3:
a) Como não foi especificado velocidade escalar média, trata-se de velocidade vetorial
média, pois velocidade é uma grandeza vetorial.
A figura mostra o deslocamento vetorial (d) entre os pontos A e B.
O módulo (d) desse deslocamento é:
d2 402 302 d 50 μm 50 106 m.
Na figura dada, contamos 10 deslocamentos sucessivos entre A e B. Assim:
Δt 10 30 Δt 300 s.
Então:
vm
d 50 106
vm 1,67 107 m/s.
Δt
300
b) Dados: I 2 D t; D kT r; k 3 1018 m3 sK; r 3 μm 3 106 m; T 300 K;
Δt 10 min 600 s.
Combinando as expressões dadas e substituindo os valores, vem:
I 2
kT
t I
r
Resposta
2
3 1018 300
3 106
da
600
I 6 104 m.
questão
4:
[D]
Página 68 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Δt
d 9 108
6 1014 s
6 1014 s
2 107 anos
7
v 1,5 104
3 10 s/ano
Δt 20.000.000 anos.
Resposta
da
questão
5:
a) Dados: ΔS 1.200 km 1.200 103 m; Δt 800 s.
vm
ΔS 1.200 103
Δt
800
vm 1.500 m/s.
b) Dados: S 32 km 32.000 m; S0 0; v0 0; t 80 s.
S S0 v0 t
aR 2
aR
t 32.000
802
2
2
Resposta
a R 10 m/s2.
da
questão
6:
[Resposta do ponto de vista da disciplina de Física]
Dados: m 60 kg; v 0; v 0 10 m/s; Δt 0,2 s.
a) A variação da energia cinética (ΔE) é:
ΔE E E0
m 2
60 2
v v02
0 102
2
2
ΔE 3.000 J.
b) Calculando o módulo da aceleração:
a
Δv
0 10
a 50 m/s2.
Δt
0,2
[Resposta do ponto de vista da disciplina de Química]
c) Reação química de decomposição da azida de sódio formando sódio metálico e
nitrogênio gasoso: 2NaN3 (s) 2Na(s) 3N2 (g).
d) Cálculo do volume V de gás nitrogênio formado pela decomposição de 65 g de
azida de sódio sob pressão atmosférica de 1 atm e temperatura de 27 C :
Página 69 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
NaN3 65
2NaN3 (s) 2Na(s) 3N2 (g)
2 65 g
3 mols
65 g
1,5 mol
T 27 273 300 K
R 0,08 atm. .mol1.K 1
P V nR T
1 V 1,5 0,08 300
VN2 36 L
Resposta
da
questão
7:
questão
8:
[C]
h
2 h 2 54
g 2
t g
2
t2
32
Resposta
g 12 m/s2.
da
Dados: f 0,25 Hz; r 2 m; VR 4 m/s; π 3.
a) Como se trata de movimento circular uniforme, somente há a componente centrípeta
da aceleração.
VT 2 π f r 2 3 0,25 2
a
VT
r
2
32
2
VT 3 m/s.
a 4,5 m/s2.
b) A figura mostra a velocidade resultante U da bola num ponto qualquer da trajetória.
Página 70 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
U2 VT2 VR2 32 42
c) cos θ
U 5 m/s.
VR 4
0,8
U 5
θ arccos0,8.
Resposta
da
questão
9:
[D]
- Espaço ocupado por cada informação:
L 0,2 μm 2 107 m.
- Comprimento de uma volta:
C 2 π r 2 3 3 103 18 103 m.
- Número de informações armazenadas em cada volta:
n
C 18 103
9 104.
L
2 107
- Como são 120 voltas por segundo, o número de informações armazenadas a cada
segundo é:
N n f 9 104 120
N 1,08 108.
Resposta
da
questão
10:
a) Dados: m 30 kg; g 10 m/s2; H 2,5 m.
Analisemos a figura a seguir:
Página 71 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Por semelhança de triângulos:
d
h
H 2,5
2 h
h 1,25 m.
H d
2
2
O sistema é conservativo. Com referencial na base do plano, vem:
A
A
A
B
B
B
EMec
EB
Mec ECin EPot ECin EPot 0 m g H ECin mg h
E EB
Cin m g H h 30 10 1,25
E 375 J.
Calculando a velocidade e a quantidade de movimento (Q) no ponto B:
m vB2
2 E 2 375
E vB2
25 vB 5 m/s.
2
m
30
Q m vB 30 5
Q 150 kg m/s.
b) Dados: m 30 kg; g 10 m/s2; cos30 0,9.
Como não há atritos a considerar, a força de contato entre o escorregador e a criança é a
força normal, de intensidade F.
F Py Pcos θ m g cos30 30 10 0,9
F 270 N.
Página 72 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
c) Dados: m 30 kg; g 10 m/s2; sen30 0,5.
A força resultante sobre a criança é a componente tangencial do peso, Px.
Fres Px m gsen θ m a m gsen30 10 0,5
a 5 m/s2.
Resposta
questão
da
11:
a) τres Fres ΔS cos α m a ΔS cos α τres d Va ΔS cos α
Como os volumes, as acelerações e as distâncias são iguais para os dois trens e
cosα = 1, vem:
τaço
τAl
daço Va ΔS
dAl Va ΔS
τaço
τAl
daço
dAl
7,9
2,7
τaço
τAl
2,93.
b) Dados: P 1,2 mW 1,2 103 W; R 10 m; π 3.
A intensidade da onda é a razão entre a potência da fonte (P) e a área abrangida (A).
Como são ondas esféricas:
I
P
P
1,2 103
I 106 W/m2
A 4 π R2
4 3 102
S 10 log
I
106
10 log
10 6
I0
1012
Resposta
S 60 dB.
da
questão
12:
5 kcal V
3L
;
; 1 cal 4 J.
a) Dados : E V
Δ
t
L
min
P
E V 5 kcal 3 L
kcal 15 4 kJ
15
V Δt
L
min
min
60 s
P 1 kW 1.000 W.
b) Dados: Δt 20 min 1.200 s.
E P Δt 1.000 1.200
E 1,2 106 J.
5 kcal
; Δt 1 min 60 s; 1 cal 4 J.
c) Dados : Pb 100 W; E V
L
A energia basal consumida em 1 min é:
Eb Pb Δt 100 60 6.000 J 1.500 cal 1,5 kcal.
Página 73 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
O volume consumido de O2 pode ser obtido por proporção direta:
5 kcal 1 L
1,5 kcal V
V
1,5
5
Resposta
V 0,3 L.
da
questão
13:
Dados: f 15 m; D 1,5 109 m; L 1,5 1011m.
a) O Sol comporta-se como objeto impróprio para o espelho, portanto a imagem formase no foco principal. Assim, p' = 15 m, conforme ilustra a figura.
Sendo D o diâmetro da imagem, por semelhança de triângulos:
D
f
D
15
15
D
9
11
DSol L
1,5 10
1,5 10
102
D 0,15 m.
b) Dados: DE 10 m; S1 1 kW/m2.
A densidade de potência (S) é a razão entre a potência recebida e a área de captação (A).
Pela conservação da energia:
S
S
P1 A1 S1
P
P A S
A
P2 A2 S
DE2 S1
2
D
100 1.000
0,152
2
π D2
π DE
S1
S
4
4
S 4,44 106 W/m2.
Página 74 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
c) Dados: m 0,6 kg 600 g; Δt 4 s; c 1 J / g K.
Como todo calor recebido é usado no aquecimento do disco de alumínio, temos:
Q P Δt m c ΔT A1 S1 Δt ΔT
ΔT
3
A1 S1 Δt
mc
102
1.000 4
4
600 1
ΔT 500 K.
Resposta
da
questão
14:
[A]
No ponto de compressão máxima, a velocidade é nula. Adotando esse ponto como
referencial de altura, nele, a energia potencial gravitacional também é nula. Assim,
aplicando a conservação da energia mecânica.
i
f
EMec
EMec
m g h d
Resposta
k d2
2
k
2 m g h d
d2
da
.
questão
15:
[E]
A energia cinética é máxima no ponto onde a energia potencial é mínima. Isso ocorre no
ponto de abscissa x x2.
Resposta
da
questão
16:
a) Dados: m 60 kg; g 10 m/s2; h 10 m.
Epot m g h 60 10 10
b)
Epot 6.000 J.
ma
V
L
kg
30
30
; m 60 kg; g 10 m/s2.
Δt
s
Δt
s
O piloto está em equilíbrio: Fa P m g 60 10 Fa 600 N.
Página 75 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
ΔQ= Fa Δt ma Δv Fa Δt
ma
Δv Fa 30 Δv 600
Δt
Δv 20 m/s.
Resposta
da
questão
17:
[C]
Dados: m 48 g 48 103 kg; g 10 m/s2; d 4 mm 4 103 m; π 3.
Na situação proposta, a força de pressão exercida pelos gases equilibra a força peso do
tubo cilíndrico e a força exercida pela pressão atmosférica sobre ele. Assim:
Fgas P Fatm pgas
pgas
48 103 10 4
3 4 10
3 2
mg
P
patm pgas
patm
A
d2
π
4
1 105 0,4 105 1 105 1,4 105 N/m2
pgas 1,4 atm.
Resposta
da
questão
18:
a) Dados: NA 6 1023; P 3,2 108 Pa; T 300 K; R 8 J/mol K.
Sendo n o número de mols, o número de partículas (N) é:
N n NA n
N
.
NA
Aplicando a equação de Clapeyron:
n RT P V
N
N NA P 6 1023 3,2 108
RT PV
NA
V
RT
8 300
N
8 1012 moléculas 3 .
V
m
b) Dados: pint p0 1 atm; ρ 103 kg/m3; h 100 m; g 10 m/s2.
A pressão suportada pela carcaça é o módulo da diferença entre as pressões externa e
interna. Assim:
Página 76 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Psub Pext Pint P0 ρ g h P0 Psub ρ g h 103 10 100
Psub 10 105 Pa.
Pnave Pint Pext P0 0 Pnave 1 atm Pnave 105 Pa.
Psub 10 105
Pnave
105
Psub
10.
Pnave
Resposta
da
questão
19:
[A]
A figura ilustra a situação, mostrando as velocidades do trabalhador e da plataforma, em
relação ao referencial fixo no solo nas situações (I) e (II).
Pela conservação da Quantidade de Movimento:
Q(I) Q(II) m M v M v ' m v ' v m v M v M v ' m v ' m v
2 m v M v M m v '
v'
2 m
M
Resposta
2 m
M v M m v '
M v
.
m
da
questão
20:
[C]
Página 77 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Dados:
PG 50.000 N; dG 3 m; dP 2 m.
Na condição de carga máxima, há iminência de tombamento, sendo nula a normal em
cada uma das rodas traseiras.
O momento resultante em relação às rodas dianteiras é nulo.
MPG M P 50.000 3 P 2
Resposta
P 75.000 N.
da
questão
21:
[D]
[Resposta do ponto de vista da disciplina de Física]
As leis de Kepler forneceram subsídios para o modelo heliocêntrico (Sol no centro)
contrapondo-se ao sistema geocêntrico (Terra no centro) até, então, defendido pela
igreja naquela época.
[Resposta do ponto de vista da disciplina de História]
Somente a alternativa [D] está correta. A questão remete ao Renascimento Científico
vinculado ao Renascimento Cultural dos séculos XIV, XV e XVI. O espírito
Renascentista é pautado pela investigação, a busca do conhecimento, seja pelo método
indutivo vinculado ao Empirismo ou ao pelo método dedutivo associado ao
Racionalismo. Questionava-se qualquer tipo de autoridade, sobretudo o poder da Igreja
que era ancorada na filosofia grega de Aristóteles. Este pensador defendia uma visão
geocêntrica de mundo e teve apoiou de outros estudiosos antigos como Ptolomeu. A
Igreja católica no medievo baseou-se no pensamento aristotélico-ptolomaico antigo e
também defendeu o geocentrismo. No entanto, alguns estudiosos do Renascimento
Científico começaram a questionar esta pseudo-visão. Entre eles estão Copérnico, 14731543, que escreveu o livro “Da Revolução Das Esferas Celestes”, em que combateu a
tese geocêntrica e defendeu o heliocentrismo e Johannes Kepler, 1571-1630, pensador
alemão que formulou três leis importantes para a Revolução Cientifica do século XVII
que consolidou o heliocentrismo. Primeira Lei: das órbitas, os planetas giram em
órbitas elípticas ao redor do sol. Segunda Lei: das áreas, um planeta girará com maior
velocidade quanto mais próximo estiver do sol. Terceira Lei: a relação do cubo da
Página 78 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
distância média de um planeta ao sol e o quadrado do período da revolução do planeta é
uma constante sendo a mesma para todos os planetas.
Resposta
da
questão
22:
[D]
Dados:
R 6 103 km 6 106 m; h 720 km 0,72 106 m; M 6 1024 kg;
G 6,7 1011 m3 /kg s2.
Como a órbita é circular, a gravidade tem a função de aceleração centrípeta.
ac g
v
GM
GM
v2
6,7 1011 6 1024
v
R h R h2
Rh
6 106 0,72 106
6,7 1011 6 1024
6,72 106
60 106 7,7 103 m/s
v 7,7 km/s.
Resposta
da
questão
23:
[E]
[I] Incorreta. Como o ciclo é anti-horário, o trabalho é negativo e seu módulo é
numericamente igual a área do ciclo.
[II] Correta. A energia interna (U) é diretamente proporcional ao produto pressão
volume. Assim: pC VC pA VA UC UA .
[III] Correta. Na transformação A B, ocorre expansão, indicando que o gás realiza
trabalho (W 0). Como há também aumento da energia interna (ΔU 0).
Pela 1ª Lei da Termodinâmica:
Q ΔU W Q 0 o gás recebe calor.
Resposta
da
questão
24:
[C]
[Resposta do ponto de vista da disciplina de Física]
Página 79 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Os conceitos básicos da Termodinâmica foram alavancados a partir de 1698 com a
invenção da primeira térmica, uma bomba d'água que funcionava com vapor, criada por
Thomas Severy para retirar água das minas de carvão, na Inglaterra. A partir daí, essa
máquina foi sendo cada vez mais aprimorada com a contribuição de vários engenheiros,
inventores e construtores de instrumentos, como James Watt. Por volta de 1760, a
máquina térmica já era um sucesso, tendo importante contribuição na Revolução
Industrial.
[Resposta do ponto de vista da disciplina de História]
A Primeira Revolução Industrial revolucionou a maneira como se produziam as
mercadorias, em especial com a criação de maquinários movidos a vapor. Na Inglaterra
da década de 1770, o mercado de tecidos, os transportes (como trens e navios) e as
comunicações funcionavam a partir de máquina a vapor. Logo, a termodinâmica está
relacionada à Revolução Industrial.
Resposta
da
questão
25:
a) Dados: ΔE m 3,6 104 J/g; m Δt 0,1g/min.
Usando análise dimensional:
W
g
ΔE ΔE m
J
J
3.600 J
P 3,6 104
0,1
3.600
Δt
m Δt
g
min
min
60 s
W 60 W.
b) Dado: m = 2,5 g.
Usando os dados e resultados do item anterior e análise dimensional, vem:
E
3.600 J
2,5 g
g
min
0,1
min
E 9 104 J.
c) Dados:
atm
J
J
p0 1 atm; V0 750 ; Cv 30
; R 0,08
8
;
mol K
mol K
mol K
T0 27 C 300 K; 1 mol 25 .
Página 80 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
O excesso de dados com valores aproximados e inconsistentes permite duas resoluções
que chegam a diferentes resultados.
Calculando o número de mols:
- Pela equação de Clapeyron:
p0 V n RT0 n
p0 V
RT
1 750
n 31,25 mol.
0,08 300
- Por proporção direta:
1 mol
25
750
n
n
750
n 30 mol.
25
Nota: por comodidade, será usado nos cálculos a seguir o segundo resultado: n = 30
mol.
- A energia liberada pela queima da vela é absorvida pelo ar na forma de calor,
aquecendo o ar do recipiente.
E Q n Cv ΔT ΔT
Q
9 104
n Cv 30 30
ΔT 100 K 100 C.
- A queima da vela ocorre a volume constante, portanto toda a energia liberada é usada
para aumentar a energia interna do gás. Como o ar deve ser tratado como gás perfeito,
usando a expressão da variação da energia interna para um gás diatômico, vem:
2 ΔU
5
9 104
E ΔU n R ΔT ΔT
2
5 n R 5 30 8
ΔT 75 K 75 C.
Nota: por comodidade, será usado nos cálculos a seguir o primeiro resultado:
ΔT 100K.
d) Aplicando a equação geral dos gases ideais:
p0 V
T0
pV
1
p
4
p atm
T0 ΔT
300 300 100
3
Resposta
da
p 1,33 atm.
questão
26:
[A]
Página 81 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
A figura mostra o traçado dos raios, determinando a posição do objeto.
Resposta
da
questão
27:
[B]
Dados:
q e 1,6 1019 C; g 10 m/s2; E 2 103 N/m; m 3,2 1015 kg.
Como a velocidade é constante, a resultante das forças que agem sobre essa esfera é
nula. Isso significa que o peso e a força elétrica têm mesma intensidade e sentidos
opostos. Assim, a força elétrica tem sentido oposto ao do campo elétrico, indicando que
a carga dessa esfera é negativa. Portanto, a esfera tem mais elétrons que prótons.
A figura ilustra a situação.
Sendo n o número de elétrons a mais, temos:
Página 82 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
F P q E m g n eE m g n
mg
3,2 1015 10
n
eE
1,6 1019 2 103
n 100.
Resposta
da
questão
28:
a) Dados: V 300 V; d 5 mm 5 103 m.
A figura ilustra os dados.
Como se trata de campo elétrico uniforme, EA = EB = EC = E.
Ed V E
V
300
60 103
d 5 103
E 6 104 V/m.
b) Da figura: xA = 1 mm e xB = 4 mm.
VAB E dAB E xB x A 6 104 4 1 103
VAB 180 V.
Como os pontos B e C estão na mesma superfície equipotencial:
VBC 0 V.
c) Dado: q 1,6 1019 C.
Analisando a figura dada: VCA VBA VAB 180V.
Página 83 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
τ q VCA 1,6 1019 180
τ 2,88 1017 J.
Resposta
da
questão
29:
questão
30:
[A]
Dado: R 0,5 kΩ 0,5 103 Ω; i 12 mA 12 103 A.
Aplicando a 1ª Lei de Ohm:
U R i 0,5 103 12 103
Resposta
U 6 V.
da
[C]
Eperd 95% Econs 0,95 Pcons Δt Eperd 0,95 60 3.600
Eperd 205.200 J.
Resposta
da
questão
31:
a) A constante α é dada pela declividade da reta.
Página 84 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
α tgθ
18 12
6
120 20 100
α 0,06
Ω
.
C
b) Dados: T0 20 C R0 12 Ω do gráfico ; i 10 A.
A 20 °C:
V R i 12 10
V 120 V.
c) À temperatura TM:
V R i 120 R 5 R 24 Ω.
Do gráfico: R 24Ω
TM 220 °C.
Resposta
da
questão
32:
A figura ilustra os pontos destacados no gráfico que são relevantes para as resoluções
dos dois itens.
a) Dados: V 0,4 V; m 5 g; Δt 4 h.
Do gráfico:
V 0,4 V C 20 mAh/g.
Q m C 5 20 Q 100 mAh.
im
Q 100
Δt
4
Q 25 mA.
Página 85 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) Dados: i 2 mA.
Do gráfico:
C 10 mAh/g V 0,2 V .
P i V 2 0,2
Resposta
P 0,4 mW.
da
questão
33:
[C]
Basta seguir a seta em cada um dos gráficos.
No gráfico da figura 1, para a potência de 150 W obtemos que a resistência é de 325Ω.
No gráfico da figura 2, para a resistência de 325Ω, obtemos a temperatura de 3.000C.
Página 86 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
34:
[D]
Considerações:
1ª) A expressão que relaciona tensão, potência e resistência é P
U2
. Com base nessa
R
expressão, se definirmos como R a resistência das lâmpadas de 120 W, as lâmpadas de
60 W e 40 W têm resistências iguais a 2 R e 3 R, respectivamente;
2ª) Na associação em série, lâmpadas de mesma resistência estão sob mesma tensão. Se
as resistências são diferentes, as tensões são divididas em proporção direta aos valores
das resistências.
3ª) Na associação em paralelo, a tensão é a mesma em todas as lâmpadas;
4ª) A tensão em cada lâmpada deve ser 110 V.
As figuras abaixo mostram as simplificações de cada um dos arranjos, destacando as
tensões nas lâmpadas em cada um dos ramos.
Arranjo (I): todas as lâmpadas estão sob tensão de 110 V.
Arranjo (II): somente uma das lâmpadas está sob tensão de 110 V.
Página 87 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Arranjo (III): todas as lâmpadas estão sob tensão de 110 V.
Resposta
da
questão
35:
[B]
A figura mostra as frequências das sucessivas notas com os respectivos índices de 1 a
14.
Página 88 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Usando a expressão do termo geral de uma progressão geométrica de razão q, temos:
1
f13 f1q12 2 f1 f1q12 q12 2 q 212 q 1,059.
f f q9
9
1
f10 f 1q
f
q9
2
n1 10
fn f1q
10
f10 f 8q2 440 f 8 1,059
7
7
7
f 8 f 1q
f8 q
f 8 f1q
440
440 f8 1,12 f 8 1,12 393 Hz.
v 340
v λ 8 f8 λ8
f 8 393
λ 8 0,86 m.
Comentário: as duas notas Dó consecutivas a que se refere o enunciado não podem ser
um Dó normal e um Dó sustenido (1ª e 2ª notas). Caso uma má interpretação levasse a
esse equacionamento, a razão da P.G. seria 2 e teríamos:
440
f10 f1 29 f 1
0,86 Hz
512
Absurdo! Um som com essa frequência não é audível para o ser humano!
Resposta
da
questão
36:
[B]
Página 89 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Como a força de atrito é a resultante das forças, podemos aplicar o teorema da energia
cinética.
final
WFat Ecin
Einicial
0
cin
m v2
1.000 202
0
2 105 J
2
2
WFat 2 105 J.
Resposta
da
questão
37:
questão
38:
[A]
Pelo Teorema de Pascal:
2
F
F d
2 1 1
F2 d2
d12 d12
F1
2
Resposta
F1 d1
F2 2 d1
F1 1
.
F2 4
da
a) Da expressão da distância percorrida no movimento uniforme:
d v Δt 2 L c Δt
Δt
2L
.
c
b) Considerações:
- como a largura de um dente é igual à largura de um espaço vazio, o comprimento da
circunferência envolvente da roda corresponde à largura de 2 N dentes;
- assim, a distância entre um ponto central entre dentes e o dente seguinte é igual à
largura de um dente.
- a frequência da roda dentada é V voltas por segundo. Então o período (T) é:
T
1
.
V
Estabelecendo proporção direta:
2 N dentes T
1 dente Δt
Δt
2 N Δt T Δt
1
T
V
2N 2N
1
.
2NV
Página 90 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
c) Dados: L = 8600 m; N = 750; V = 12 voltas por segundo.
Os intervalos de tempo calculados nos itens anteriores são iguais.
Então:
2 L
1
c
2 NV
c 4 L N V 4 8.600 750 12 309.600.000
c 3,1 108 m/s.
Resposta
da
questão
39:
a) Dados: vN = 2 km/h; vS = 6 km/h; tN = 2 h; ΔS dcidades 48km.
Sendo vemb a velocidade da embarcação em relação às águas, a velocidade da
embarcação (v) em relação às margens é:
v v emb vágua .
Para o Rio Negro:
v1
ΔS
Δt
vemb vN
ΔS
tN
vemb
ΔS
48
vN v emb
2
tN
2
ΔS
tS
26 6
v emb 26 km/h.
Para o Rio Solimões:
v2
ΔS
Δt
vemb vS
48
tS
20
48
tS
tS
48
20
tS 2,4 h 2 h e 24 min.
b) Dados: ρN 996 kg / m3; ρS 998 kg / m3.
Pelo Teorema de Stevin:
pN pat dN g h
p pat dS g h
S
Δp pS pN dS dN g h 998 996 10 5
Δp 100 N/m2 .
Resposta
da
questão
40:
a) Dados: d1 = 1 km = 1.000 m; v2 = 7,2 km/h = 2 m/s; Δt2 2min 120s.
A distância total (d) percorrida nas 8 vezes é:
Página 91 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
d 8 d1 d2 8 d1 v 2 Δt 2 8 1.000 2 120 8 1.240
d 9.920 m.
b) Dados: v0 = 0; v1 = 10,8 km/h = 3 m/s; ΔS 3m.
Aplicando a equação de Torricelli:
v12 v02 2 a ΔS a
v12 v02 32 0 9
2 Δs
23
6
a 1,5 m/s2.
Resposta
da
questão
41:
a) No gráfico, nota-se que o movimento de Batista é uniformemente variado.
Entendendo como aceleração o módulo da componente tangencial da aceleração ou a
aceleração escalar, tem-se:
aB
ΔvB
40
4
1
ΔtB 20 0 20 5
aB 0,2 m/s2.
b) No gráfico velocidade x tempo, a distância percorrida é numericamente igual à
“área” entre a linha do gráfico e o eixo dos tempos.
Assim:
50 5
dA 125 m.
dA 2
d 50 30 4 d 160 m.
B
B
2
c) A velocidade escalar média de Arnaldo no intervalo pedido é:
vA
dA 125
Δt A
50
Resposta
v A 2,5 m/s.
da
questão
42:
[C]
Dados: f = 300 rpm = 5 Hz; π = 3; R = 60 cm = 0,6 m.
Página 92 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
A velocidade linear do ponto P é:
v ω R 2 f R 2 3 5 0,6
v 18 m/s.
Resposta
da
questão
43:
[E]
Se a velocidade é nula, a aceleração (a) tem direção tangencial, formando com a
vertical ângulo de 60°, como indicado na figura.
A resultante é a componente tangencial do peso. Aplicando o Princípio Fundamental da
Dinâmica:
1
Px m a m gcos60 m a a 10
2
a 5 m/s2.
Resposta
da
questão
44:
a) Dados: P = 4 W; Δt 5 s.
E P Δt 4 5
E 20 J.
b) Dados: m = 0,2 kg; R 5 cm 5 102 m.
A energia cinética das duas esferas é:
Página 93 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
m v2
2
m ω R E m ω2 R2
2
1 E
1
20 100
ω
100
2
R m 5 10
0,2
5
E2
ω 200 rad/s.
c) A aceleração (a) da esfera tem duas componentes: tangencial (aT ) e centrípeta (aC ).
- Componente tangencial:
v aT t ω R aT t aT
ω R 200 5 102
t
5
aT 0,2 m/s2.
- Componente centrípeta:
aC ω2 R 2 102
2
5 102 4 104 5 102 aC 2 103 m/s2.
Comparando os valores obtidos, a componente tangencial tem intensidade desprezível.
Então a intensidade da resultante é igual à da componente centrípeta.
aT aC a aC 2 103 m / s2.
Aplicando o Princípio Fundamental da Dinâmica:
Fres m a 0,2 2 103 0,4 103
Fres 400 N.
d) α
aT
2
0,4 102 α 40 rad/s2.
R 5 102
Resposta
da
questão
45:
[B]
A normal, que age como resultante centrípeta, no pé de uma pessoa tem a mesma
intensidade de seu peso na Terra.
N Rcent P m ω2 R m g ω
g
10
1
r
100
10
ω 0,3 rad/s.
Página 94 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
46:
Nota: o termo órbita em torno do Sol é redundante, pois a órbita já é em torno de
algo.
a) a força que o satélite exerce sobre a Terra é desprezível. Então, a resultante centrípeta
sobre a Terra é a força gravitacional que o Sol exerce sobre ela, conforme indica a
figura.
Rcent FST MT ω2T R
ωT
G MS
R3
G MS MT
2
R
ωT2
G MS
R3
.
b) O período de translação do satélite é igual ao período de translação da Terra:
TA TT 1ano 3,14 107 s.
ωA
2π
2 3,14
TA
3,14 107
ωA 2 107 rad/s.
c) A força resultante gravitacional sobre o satélite é a soma vetorial das forças
gravitacionais que o satélite recebe do Sol e da Terra, conforme ilustra a figura.
Página 95 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Fres FS FT
G MS m
R d2
G MT m
d2
M
M
S
Fres G m
T .
R d2 d2
Resposta
da
questão
47:
a) A área total é igual à soma das áreas das seis faces.
A 2 2 3 2 4 3 4
A 52 m2.
b) Dados: k 5 102 J(s m C); ε 26cm 26 102m; Ti 20C; Te 40C.
Para manter a temperatura constante, a potência do aquecedor deve compensar o fluxo
de calor para o meio.
Assim:
PΦ
2
k A ΔT 5 10 52 20 -40
6 102 W
ε
26 102
P 0,6 kW.
c) Da expressão da energia consumida:
E P Δt 0,6 24
Resposta
E 14,4 kWh.
da
questão
48:
[C]
Dados: Pco = 10 W; ET = 2.500 kcal = 2,5 106 cal; 1 cal = 4 J.
Página 96 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Calculando a potência total:
E
2,5 106 4
PT T
115,74 W 116 W.
Δt
24 3 600
116 W 100%
10 W x%
x 8,62%
x 9%.
Resposta
da
questão
49:
a) Quando x xB yB 0.
Assim:
1
log 1 x 4 0 log 1 x 4
2
2
2
4
x x 24
x 16 unidades de comprimento.
b) Usando a expressão da Energia Mecânica:
Emec Ecin Epot Emec
v2
M v2
M g y Emec M
g y
2
2
v2
Emec M
10 y unidades de energia.
2
c) Como o corpo parte do repouso em x = 1, temos v0 = 0.
Na expressão dada, para x = 1, temos:
y log 1 1 4 0 4 y 4.
2
Aplicando esses dados na expressão obtida no anterior:
v2
02
Emec M
10 y Emec M
10 4
2
2
Emec 40 M.
Pela conservação da Energia Mecânica:
Página 97 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
2
v
v2
v2
M 10 log 1 x 4 40 M
40 10 log 1 x 40
-10 log 1 x
2
2
2
2
2
2
v
-20 log 1 x .
2
Caso queiramos eliminar o sinal (–) do radicando, podemos mudar o logaritmo para a
base 2:
log 1 x
2
log2 x log2 x
1
1
log2
2
log 1 x log2 x.
2
Assim:
v
20 log2 x unidades de velocidade.
Resposta
da
questão
50:
a) Dados: v = 72 km/h = 20 m/s; C = 35 MJ/L = 35 106 J/L;
η 30% 0,3; Δt 1h 3.600s.
Como a velocidade é constante, a força motriz tem a mesma intensidade da força de
resistência do ar. Assim, a energia útil (EU) é igual ao trabalho realizado pela força
motriz.
EU τF F ΔS F v Δt EU 380 20 3.600 EU 2,74 107 J.
Calculando a energia total (ET):
E
η U
ET
E
2,74 106
ET U
η
0,3
ET 9,12 107 J.
Por proporção direta, calculamos o consumo de gasolina:
35 106 J
1L
7
9,12 10 J V
V
9,12 107
35 106
V 2,6 L.
b) Dados: N = 2.500 N; R = 30 cm; d = 0,3 cm.
O torque total em relação ao ponto O deve ser nulo. Então, em relação a esse ponto, o
somatório dos momentos horários é igual ao somatório dos momentos anti-horários.
Assim:
Página 98 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Fat R N d Fat
N d 2.500 0,3 2.500
R
30
100
Fat 25 N.
Resposta
da
questão
51:
[B]
Dados: m = 70 kg; v0 = 10 m/s; ΔEC 0,7(500) 350J.
A energia cinética depois do salto é igual à energia cinética inicial somada à variação
adquirida no salto.
f
EC
EiC ΔEC
70 v 2 70 10
350
2
2
2
m v 2 m v02
ΔEC
2
2
35 v 2 35 100 350 v 2 100 10 v 110
v 10,5 m/s.
Resposta
da
questão
52:
a) Dados: D = 60 km = 6.000 m; C = 80 cal/m; ET = 2.000 kcal.
Calculando a energia consumida (E1) em uma caminhada:
80 cal
1 m
6.000
m
E1
E1 6.000 80 480.000 cal E1 480 kcal.
Para a percentagem P temos:
100%
P%
2.000 kcal
480 kcal
P
100 480
2.000
P 24%.
b) Dados: M = 80 kg; g = 10 m/s2; h = 300 m.
Da expressão da energia potencial:
C m g h 80 10 300 C 2,4 104 J
24 104 J
4 J/cal
C 6 104 cal.
c) Dados: m = 2,4 kg = 2400 g.
Página 99 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Do Note e adote, para perder 2400 g de gordura terá que queimar a quantidade de
energia:
E 2400 9 21600 kcal.
Estabelecendo proporção direta:
480 kcal
1 caminhada
N caminhadas 21600 kcal
N
21600
480
N 45.
Resposta
da
questão
53:
questão
54:
[D]
Somando os percentuais indicados em cinza:
9,1% + 13,5% + 18,5% + 5,5% = 46,6%.
557 milhões 100%
46,6%
x milhões
x
557 46,6
100
x 259,562 milhões.
Resposta
da
[A]
Lembrando as expressões das forças mencionadas:
P m g P dcorpo V g
E dlíq Vim g
Considerando os cilindros homogêneos, o Peso e o Empuxo são aplicados no centro de
gravidade de cada um. O empuxo tem a mesma densidade nos dois casos, pois os
volumes imersos são iguais, mas o Peso do cilindro mais denso é maior. Assim, o
Empuxo no conjunto é aplicado no ponto médio (B) e o Peso do conjunto fica deslocado
para direita. As figuras ilustram a situação.
Página 100 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Comentário: Essa posição horizontal não é a de equilíbrio do conjunto. Assim que
abandonado, ele sofrerá um giro no sentido horário, ficando em equilíbrio estável na
vertical, com o cilindro mais denso totalmente imerso e o menos denso parcialmente
imerso, pois, para que o conjunto funcione como boia, sua densidade deve ser menor
que a da água.
Resposta
da
questão
55:
[C]
No equilíbrio, o empuxo sobre o bloco tem a mesma intensidade do peso do bloco.
A água que extravasa cai no copo, portanto o volume deslocado de água é igual ao
volume que está no copo.
m dágua Vdesloc
E dágua Vdesloc g
P M g
E P dágua Vdesloc g M g dágua Vdesloc M
m M.
Resposta
da
questão
56:
a) Dados:
V 1.800 cm3 1,8 103 m3; m 6 kg 6 103 g; M 44 g / mol; R 8,3 J / mol K; T 300 K.
Da equação de Clapeyron:
p V
m R T 6 103 8,3 300
m
R T p
M
VM
1,8 103 44
p 1,89 108 N/m2.
Página 101 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
b) Dados: m = 50 g; v = 20 m/s.
Estimando a massa do extintor: Mext = 10 kg = 10.000 g.
Como se trata de um sistema mecanicamente isolado ocorre conservação do momento
linear. Assim, em módulo:
Mext V m v V
m v 50 20
Mext 10.000
Resposta
V 0,1 m/s.
da
questão
57:
[C]
A energia cinética da partícula vale Eα .
Então:
mα vα2
Eα
2
4 vα2
Eα
2
vα
Eα
.
2
Como o sistema é mecanicamente isolado, temos:
mα vα mPb vPb 4
2
vPb
Eα
1 Eα
200 vPb vPb
2
50 2
Eα
.
5 000
Assim:
EPb
2
mPb vPb
Resposta
2
EPb
E
200 Eα
EPb α .
2 5 000
50
da
questão
58:
a) Dados: re = 42.000 km; π 3.
Como o satélite é geoestacionário, seu período orbital é igual ao período de rotação da
Terra:
T = 24 h.
Calculando a intensidade da aceleração centrípeta:
Página 102 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
2
4 π2
4 32
2π
ac ω2 re
re ac
42.000
42.000
576
T
242
1.000 m
ac 2.625 km/h2 ac 2.625
3.600 s2
ac 0,2 m/s2.
b) Dados:
re 42.000km 42 106 m; M 6 1024 kg; G 6,7 1011kg m2 / kg2; rc 7.000 km 7 106 m.
G M m G M m
G M m 1 1
Ead Ee Ec
Ead
2 re rc
2 re 2 rc
Ead
6,7 1011 6 1024 2 102 1
1
6
2
7 106
42 10
1 6
2 1017
Ead 40,2 1015
E
ad
42 106
42 106
Ead 4,8 109 J.
Resposta
da
questão
59:
[D]
Coeficiente de dilatação linear do bronze é maior que o do ferro, portanto a lâmina de
bronze fica com comprimento maior, vergando como mostrado na alternativa [D].
Resposta
da
questão
60:
a) Dados: P 1.400W; η 50% 0,5; Δθ 20 C; m 100g; ca 4,2J / g C.
Calculando a potência útil:
PU η PT 0,5 1.400 PU 700 W.
Da expressão da potência térmica:
Página 103 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
PU
Q
Δt
Δt
Q m ca Δθ
100 4,2 20
Δt
PU
PU
700
Δt 12 s.
b) Dados: L = 30 cm; v c 3 108 m / s
Observando a figura dada, concluímos que entre as paredes cabem 2,5 comprimentos de
onda. Assim:
2,5 λ L
λ
30
2,5
λ 12 cm 12 102 m.
Da equação fundamental da ondulatória:
vλ f f
v
3 108
0,25 1010 Hz 2,5 109 Hz
λ 12 102
f 2,5 GHz.
Resposta
da
questão
61:
a) Sendo a lente convergente e o objeto muito distante (impróprio), a imagem forma-se
no foco imagem. Assim:
f p' 5 cm.
Para a nova situação, a imagem é p’’. Aplicando a equação dos pontos conjugados:
1 1 1
f p p''
1
1
1
5 100 p''
1 20 1 19
p''
100
100
p''
100
cm.
19
A variação na posição da imagem é:
p'' p'
100
100 95
5
19
19
p'' p'
5
cm.
19
b) Dados: n = 3; C = 0,6 pF; V = 5 V.
Para uma associação de n capacitores de mesma capacitância C, a capacitância
equivalente é:
Ceq
C 0,6
n
3
Ceq 0,2 pF.
Calculando a carga armazenada:
Página 104 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Q Ceq V 0,2 5
Q 1 pC 1 1012 C.
Resposta
da
questão
62:
a) A área do sensor é A 6 6 36 mm2, e o número de pixels é N 500 500 25 104.
Assim, a área (A1) de cada pixel é:
A1
A
36
N 25 104
A1 1,44 104 mm2 .
b) Dados: f = 50 mm; p’ = d = 175 mm.
Da equação dos pontos conjugados:
1 1 1
1 1 1
p' f
p
f p p'
p f p'
p' f
L
df
175 50
df
125
L 70 mm.
c) Da equação do aumento linear transversal, em módulo:
y'
p'
y
p
D' d
6 175
D L
D 70
D
420
175
D 2,4 mm.
Resposta
da
questão
63:
[D]
A figura mostra as forças atrativas e repulsivas agindo sobre a carga A, bem como a
resultante dessas forças.
Página 105 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
64:
[D]
Dado: A2 = 2 A1.
Combinando a primeira e a segunda lei de Ohm:
ρL
i
V1 R1 i V1
A1
V R i V ρ L i
2
2
2
2 A1
V1 ρ L i
2 A1
V2
A1
ρLi
V1
2
V2
V1 2 V2 .
Resposta
da
questão
65:
a) Dados: R 1,5Ω; ρ 64,8 108 Ω m; A 1,296 108 m2.
Da segunda lei de Ohm:
R
ρL
A
L
R A 1,5 1,296 108
1,5 0,02 0,03 m
ρ
64,8 108
L 3 cm.
b) Do gráfico da Figura 1, conforme ponto assinalado:
f = 8 MHz e R 4Ω H 35Oe.
Do gráfico da Figura 2, conforme ponto assinalado:
Página 106 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
H 35Oe μr 1.000
Substituindo os valores obtidos na expressão fornecida:
δk
64,8 108
ρ
δ 500
500 81 1018 500 9 109 δ 4,5 106 m
3
6
μr f
10 8 10
δ 4,5 μm.
Resposta
da
questão
66:
O gráfico destaca os valores relevantes para a resolução da questão.
a) Como o resistor e a lâmpada estão em série, a corrente é a mesma nos dois.
Do gráfico:
V 2,5 V iR i 0,04 A.
b) A força eletromotriz da bateria é E = 4,5 V. A tensão no resistor é VR.
Página 107 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
VE E VR 4,5 2,5 VR 2,0 V.
Aplicando a 1ª lei de Ohm:
VR R i R 2 R 0,04 R
2
0,04
R 50 Ω.
c) Com a nova bateria (E’ = 3 V), para a potência total PT = 60 mW, a corrente na
lâmpada é i' .
P E' i'
i' i'R 20 mA 0,02 A 2 102 A.
60 3 i'
A potência PR dissipada no resistor é:
2
PR R i'R
50 2 102
2
50 4 104 20 103 W
PR 20 mW.
Resposta
da
questão
67:
[E]
Como as partículas estão eletrizadas positivamente, a força elétrica FE tem o mesmo
sentido do vetor campo elétrico. A força magnética FM , pela regra prática da mão
direita nº 2 (regra do “tapa”) é em sentido oposto ao da força elétrica, como mostra a
figura.
Nas partículas do grupo 3, a força magnética é equilibrada pela força elétrica, ou seja:
q v3 B q E v3
E
.
B
Página 108 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Nas partículas do grupo 1, a força magnética é menos intensa que a força elétrica.
q v1 B q E v1
E
B
v1 v3 .
Nas partículas do grupo 2, a força magnética é mais intensa que a força elétrica.
q v2 B q E v2
Conclusão: v1 v3
Resposta
E
B
v 2 v3
v3
E
v2 .
B
E
v2 .
B
da
questão
68:
[B]
Notemos que a escala de nível sonoro cresce de cima para baixo. A área em cinza
representa a região de audição de cada uma das orelhas.
[I] Falsa. Analisando os gráficos, concluímos que sons de frequência 6 kHz e nível
sonoro de 20 dB não são ouvidos pela orelha direita, mas o são para o orelha esquerda.
[II] Verdadeira. Os gráficos mostram que sussurros de frequência 0,25 Hz e nível de
15 dB são ouvidos pelas duas orelhas.
Página 109 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
[III] Falsa. A diminuição da capacidade auditiva não ocorre pela degeneração dos ossos
descritos acima, assim como estes não estão na orelha externa e sim no ouvido médio.
Resposta
da
questão
69:
questão
70:
[B]
Dados: c = 3 108 m/s; f = 40 MHz = 4 107 Hz.
Da equação fundamental da ondulatória:
λ
v 3 108
f 4 107
Resposta
λ 7,5 m.
da
[A]
Dados: v = 330 m/s; f = 440 Hz.
Se o Sr. Rubinato não está mais ouvindo o Lá é porque está ocorrendo interferência
destrutiva. Para que ocorra tal fenômeno é necessário que a diferença de percurso entre
o ouvinte e as duas fontes ( no caso,
comprimentos de onda. O menor valor de
) seja um número ímpar (i) de meios
é para i = 1.
Página 110 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
2
v
f
2
330
2 400
0,375 m
38 cm.
Resposta
da
questão
71:
[B]
Dados: D1 = 540 m; v1 = 10,8 km/h = 3 m/s; D2 = 720 m; v2 = 14,4 km/h = 4 m/s; Δtc =
30 min.
Calculando o tempo total:
D1 540
Δt1 v 3 180 s 3min.
1
D2 720
180 s 3min.
Δt2
v2
4
Δt 30min.
c
Δt Δt1 Δt 2 Δtc 3 3 30
Δt 36min.
Resposta
da
questão
72:
[D]
Dados: M = 500 kb; h1 = 220 m; h2 = 400 m; g = 10 m/s2.
A variação da energia potencial é:
ΔEP M g h2 M g h1 M g h2 h1 ΔEP 5 000 10 400 220
ΔEP 9 106 J.
Resposta
da
questão
73:
[Resposta do ponto de vista da disciplina de Química]
a) Teremos:
Página 111 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Para n mols de butano:
1 mol C4H10
n
58 g
mC4H10
mC4H10 58n g
Para n mols de propano:
1mol C3H8
n
44 g
mC3H8
mC3H8 44n g
mC4H10 mC3H8 1,02 g
58ng 44ng 1,02g
n 0,01mol
ntotal 2n 2 0,01 0,02 mol
b) Para a mistura de propano e butano, teremos:
24 L
1 mol
V
0,02 mol
V 0,48 L 480 mL
V(volume)
t (tempo)
480
mL
48 mL.min1
t
t 10 min
Vazão do gás
c) Teremos:
Página 112 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
t 10 min 10 60 s 600 s
S
Velocidade
t
S
2,5m.s1
600s
S 1500 m
ou
S 1,5 103 m
[Resposta do ponto de vista da disciplina de Física]
a) Química.
b) Química.
c) Dado: vm 2,5 m/s.
Do item anterior: t 10 min 600 s.
D vm Δt 2,5 600 D 1.500 m.
Resposta
da
questão
74:
a) Dados: c = 3 108 m/s; H = 2,3 10–18 s-1; Δλ 0,092 λ0 .
Combinando as duas expressões dadas:
v H r
c Δλ
v λ
0
Hr
c Δλ
λ0
r
3 108 0,092 λ 0
c Δλ
H λ0
2,3 108 λ 0
r 1,2 1025 m.
b) Dados: E = 3,24 1048 J; mfinal = 4 1030 kg.
Calculando a massa consumida para produzir essa energia:
E mc 2 m
E
c
2
3,24 1048
3 10
8 2
3,24 1048
16
9 10
m 3,6 1031 kg.
minicial mfinal m minicial 4 1030 3,6 1031 4 1030 36 1030
minicial 4 1031 kg.
Página 113 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
75:
a) Analisando o gráfico 1, referente à terceira corrida, teremos:
ΔS 7,5km
Δt 0,5h
ΔS 7,5km
V
V 15 km
h
Δt
0,5h
Com a velocidade do atleta, teremos a constante CMET do gráfico 2:
V 15
km
kJ
CMET 60
h
kg.h
E CMET .m.t = 60.70.0,5 E = 2100kJ
Resposta: E = 2,1x103 kJ
b) Considerando que o pé de um adulto possui aproximadamente 0,1m x 0,25m,
podemos estimar sua área: A 0,1x0,25 2,5x102 m2 .
Cálculo da pressão:
F
A
F Peso m.g
m.g
70.10
P
2,8x104 N 2
A
m
2,5x102
P
Resposta: P 2,8x104 Pa
Resposta
da
questão
76:
a) Como V ΔS , teremos:
Δt
V
ΔS
1,5x1011
3,0x108
Δt 0,5x103 s
Δt
Δt
Resposta: Δt 5,0x102 s
b) T mg Fe 0
Página 114 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Tg45
Fe
F
1 e Fe mg
mg
mg
Como Fe k
Fe mg k
q2
d2
q2
d2
:
mg
De acordo com o enunciado:
k = 9 109 N m2/C2
d = 3 cm = 3x10-2 m
m = 0,004 g = 4x10-6 kg
g = 10 m/s2
Substituindo os valores:
k
q2
d2
mg
9x109.q2
(3x102 )2
4x106.10 q2 4x1018
Resposta: | q | 2,0x109 C
Resposta
da
questão
77:
questão
78:
[C]
Velocidade média do atleta com a ajuda do vento:
Δs 100m
Δt
9.9s
v 10.1m s
v
Resposta
da
a) Dado: f = 33 rpm.
Página 115 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
f
33 rot 33 rot
min
60 s
f 0,55 Hz.
ωf 2 π f ωf 2 3 0,55 ωf 3,3 rad / s.
b) Dados: α = 1,1 rad/s2; ω0 = 0.
Da equação da velocidade angular para o movimento circular uniformemente variado:
ω
3,3
ωf ω0 α t f t f f
t f 3 s.
α
1,1
c) Dados: μ e = 0,09; g = 10 m/s2; r = 10 cm = 0,1 m.
A componente de atrito da força que o disco aplica na caixa de fósforos exerce a função
de resultante centrípeta. A caixa começa a se deslocar em relação ao disco no instante
em que a força de atrito atinge intensidade máxima.
Da figura:
Fmáx Fcent
at
r es
N P m g
ωc
μe g
2
2
μe N m ωc r μe m g m ωc r
ωc
r
ωc 3 rad / s.
0,09 10
9
0,1
d) Aplicando os resultados obtidos nos itens anteriores na equação de Torricelli para o
movimento circular uniformemente variado:
ωc2 ω02 2 α Δθ Δθ
ωc2
32
2 α 2 1,1
Δθ 4,1 rad.
Página 116 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
79:
a) Dados: m = 1000 kg; v0 = 6000 m/s; v = 0; Δt = 7 min = 420 s.
Da segunda lei de Newton, para a força resultante tangencial:
v
0 6000
6 106
Fres m a Fres m
1000
t
420
4,2 102
Fres 1,43 104 N.
b) Dados: m = 1000 kg; h0 = 125 km = 125 103 m; h = 100 km = 100 103 m; v =
4000 m/s; v0 = 6000 m/s; gMarte = 4 m/s2.
Sendo WFat o trabalho da força de atrito, aplicando o Teorema da Energia Mecânica:
m v2
m v02
final
inicial
WFat EMec
EMec
WFat
m gMarteh
m gMarteh0
2
2
m 2
WFat
v v02 m gMarte h h0
2
1000
WFat
40002 60002 1000 4 100 125 1000
2
WFat 500 2 107
4 106 25
1 1010 1 108
WFat 1,01 1010 J.
Resposta
da
questão
80:
a) Dados: π 3; g = 10 m/s2; ρágua = 1,0 103 kg/m3; b = 1,6 10-3 N.m.
Na iminência de começar a cair, a força exercida pelo vento ascendente tem mesma
intensidade que o peso. Lembrando que o volume de uma esfera de raio r é
V
4
π r 3 , vem:
3
P Fvento m g b r ρágua V g b r ρágua
r
b
1,6 103
4 108
4
3 4
ρágua π g
10 3 10
3
3
4
π r3 b r
3
r 2 104 m.
b) Dados: A = 1 m2; h = 20 mm = 20 10–3 m; ρágua = 1,0 103 kg/m3; v0 = 2,5 m/s; v =
0.
Página 117 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
O volume de água despejado nessa área é:
V A h 1 20 103 m3.
Calculando a massa correspondente:
m ρágua V 103 20 103 m 20 kg.
Pelo Teorema do Impulso:
I ΔQ I m v v0 20 0 2,5
I 50 N s.
Resposta
da
questão
81:
[B]
No ponto considerado (B), a componente tangencial da resultante é nula, restando
apenas a componente centrípeta, radial e apontando para o centro da curva (P). Portanto,
a força resultante tem direção vertical, com sentido para cima.
Resposta
da
questão
82:
a) Dados: PT = 100 GW = 100 109 W; I = 250 W/m2.
P
100 109
A T
I
250
P
I T
A
A 4 108 m2.
b) Dados: P = 0,8 PT; 1 ano = 3 107 s.
EB P t EB 0,8 PT t 0,8 100 109 3 107
EB 2,4 1018 J.
c) Dado: equivalente energético do petróleo igual a 4 107 J/L.
4 107 J
18
2,4 10 J
1L
V
V
2,4 1018
4 107
V 6 1010 L.
d) Dado: c = 3 108 m/s.
E
2,4 1018 2,4 1018
EB m c 2 m B
2
c2
9 1016
3 108
m 26,7 kg.
Página 118 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
83:
questão
84:
[B]
2
1
1
2πR
E MVP2 E M
2
2
T
2
1
2.3.10
50000
45000000
E 50000
900
2
2
2
2
E 22500000J
E 2,25 107 J
Resposta
da
[A]
Utilizando o teorema do impulso temos:
I F Δt m ΔV
De forma escalar temos:
I F Δt m Δv
m Δv
F
Δt
Analisando esta última expressão, podemos concluir que para a frenagem do veículo a
força é inversamente proporcional ao tempo da colisão. A colisão direta da cabeça do
motorista no volante ocorre em um intervalo de tempo muito pequeno, o que resulta em
uma grande força de impacto. Entretanto, o airbag aumenta o tempo de colisão
(frenagem da cabeça do motorista), o que diminui a força do impacto.
Resposta
da
questão
85:
[E]
Pelo Teorema do Impulso, a intensidade da força média (Fm) é dada pela razão entre o
módulo da variação da quantidade de movimento (|v|) e o tempo de interação (t). A
Página 119 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
pressão média (pm) é dada pela razão entre intensidade da força média e a área de
contato (A). Assim:
m Δv
Fm
Δt
p Fm
m A
I
II
I em II: pm
m Δv
.
Δt A
Dados: mV = 270 g; mG = 45 g; v0V = 30 m/s; vV = 0; v0G = 60 m/s; vG = 0; tV = 2 tG;
AV = 10 AG.
Então, fazendo a razão entre as pressões exercidas pela bola de golfe (pmG) e pela bola
de vôlei (pmV):
pmG mG ΔvG Δt V A V
pmG 45 0 60 2 ΔtG 10 AG
pmV
ΔtG AG mv Δv V
pmV
ΔtG AG
270 0 30
pmG 6,7 pmV pmG pmV .
Resposta
da
questão
pmG 20
pmV
3
86:
[A]
Pela conservação da quantidade de movimento:
pe pf final pe pf inicial.
Mas, antes da colisão, apenas o fóton apresenta quantidade de movimento, que tem
direção e sentido do eixo x. Então:
pe pf final pf inicial.
A figura mostra três possibilidades.
Nota-se que a figura (II) está de acordo com a opção [A].
Página 120 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
87:
Dados: M = 6 1024 kg; m = 1016 kg; v0 = 30 km/s = 3 104 m/s; 1 megaton = 4
1015 J.
a) Pi m v0 1016 3 104 Pi 3 1020 kg m / s.
16
m v02 10
b) Ec
2
3 104
2
2
Ec 4,5 1024 J.
c) Trata-se de um choque inelástico. A massa do meteoro é desprezível em relação à
massa da Terra, por isso, depois do choque, a massa do sistema é apenas a massa da
Terra, pois:
6 1024 1016 6,00000001 1024 6 1024.
Pela Conservação da Quantidade de movimento:
Antes
QSist
QDepois
m vo M m v v
Sist
m v0 3 1020
5 105 m / s
24
M
6 10
v 0.
O choque do meteoro com a Terra praticamente não altera a velocidade da Terra.
d) Pela resposta do item anterior, conclui-se que toda energia cinética do meteoro é
dissipada na colisão. Passando para megaton:
4 1015 J 1 megaton
24
Edissip
4,5 10
Edissip
4,5 1024
4 1015
Edissip 1,125 109 megaton.
Resposta
da
questão
88:
a) Dados: I = 400 W/m2; A = 2 m2; Δt = 1 min = 60 s.
Calculando a quantidade de calor absorvida e aplicando na equação do calor sensível:
Q I A Δt Q 400 2 60 48.000 J.
Q m c Δθ Δθ
Q
48000
m c 6 1000
Δθ 8 C.
b) Dados: T1 = 290 K; T2 = 300 K; ρ1 = 1,2 kg/m3.
Página 121 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Sendo a pressão constante, da equação geral dos gases:
V1 V2
T1 T2
m
m
ρ1 T1 ρ2 T2
ρ2
ρ1 T1
T2
1,2 290
300
ρ2 1,16 kg / m3 .
Resposta
da
questão
89:
da
questão
90:
[D]
r
PP
PT
3.103
3
100.10
3
100
r 3%
Resposta
[A]
Dados: Fórmula do etanol = C2H5OH; Massas molares = C(12g/mol), H(1g/mol),
O(16g/mol); m = 138 g
Calculando a massa molar do etanol:
M = 2(12) + 5(1) + 16 + 1 = 46 g.
O número de mols contido nessa amostra é:
n
m 148
M 36
n 3.
Analisando o gráfico, notamos que durante o aquecimento a energia absorvida na forma
de calor sensível (QS) e a correspondente variação de temperatura () são,
respectivamente:
QS 35 kcal; 78 (18) 96 C.
Aplicando a equação do calor sensível na forma molar:
QS n cL cL
Q
35
n 3 96
cL 0,12 kJ / mol C.
Ainda do gráfico, a quantidade de calor absorvida durante a vaporização (QV) é:
Q 145 35 110 kJ.
V
Aplicando a equação do calor latente, também na forma molar:
Página 122 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Q
110
QV n LV LV v
n
3
Resposta
LV 36,7 kJ / mol.
da
questão
91:
a)
b) Embora o examinador quisesse os traçados numa mesma figura, para melhor
visualização, foi construída uma segunda figura.
c) Dado: β 44.
Na figura acima, cada lado de α é perpendicular a cada lado de β. Então:
α β 44.
Página 123 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
O
triângulo
ABC
é
retângulo.
Então:
γ 2 α 90 180 γ 2 44 90 180 γ 180 90 88
γ 2.
d) Dado: AC = 10 cm; sen (22°) = 0,37; cos (22°) = 0,93; sen (44°) = 0,70; cos (44°) =
0,72;
sen (88°) = 0,99; cos (88°) = 0,03.
Do item anterior, γ 2. Da trigonometria:
sen 2° = cos 88° = 0,03; cos 2° = sen 88° = 0,99.
No triângulo ABC:
AC
AB
AB 330 cm.
tg γ
sen 2 10
cos2 AB
Resposta
0,03 10
0,99 AB
da
1
10
33 AB
questão
92:
a) Dados: P0 = 24 W; d = 2 m; π 3; θ 60.
Combinando as expressões dadas:
I I cos2 θ
0
P0
I0
4π d2
I
P0
4π d2
cos2 θ
24
4 3 22
cos2 60
2
1 1
1
2 2
8
I 0,125 W / m2.
b) Dados: θB 60; θB θr 90; n1 1.
θB θr 90 60 θr 90 θr 30.
Na lei de Snell:
n1 sen θB n2 sen θr n1 sen 60 n2 sen 30 1
3
1
n2
2
2
n2 3.
Resposta
da
questão
93:
[A]
Página 124 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Utilizando a equação de Gauss temos:
1 1 1
f P P'
Observando a ilustração temos:
P 3 cm e f 2 cm
1 1 1
1 1 1 32
2 3 P'
P' 2 3
6
1 1
P' 6 cm
P' 6
Sabendo que P' é positivo, concluímos que a imagem é REAL. Vejamos agora se a
imagem é direita ou invertida.
P' 6 cm
P
3 cm
A 2
A
Logo, a imagem é duas vezes maior (fator 2) que o tamanho do objeto, porém é
invertida (sinal negativo).
Observando a imagem apresentada, podemos observar que o objeto tem 2 cm de altura,
logo sua imagem será invertida e de tamanho igual a 4 cm.
Assim concluímos que a imagem será é REAL, INVERTIDA e de tamanho igual a 4
cm.
Resposta
da
questão
94:
[E]
Analisando cada uma das afirmativas.
I. Incorreta. A figura ilustra os perfis adquiridos pela microlente com os tempos
Página 125 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
crescentes de aquecimento.
Nota-se nela que R3 < R2 < R1. Assim, o raio de curvatura da microlente diminui com
os tempos crescentes de aquecimento.
II. Correta. De acordo com a equação do fabricante de lentes (I), a vergência (V) de
uma lente plano convexa é dada pela expressão:
nlente
1
1
(I)
V
nmeio
R
1
f V (II)
Ela nos mostra que à medida que o raio de curvatura diminui a vergência aumenta. A
expressão (II) mostra que a distância focal é o inverso da vergência. Portanto, a
distância focal da microlente diminui com os tempos crescentes de aquecimento.
III. Correta. Como são lentes plano-convexas imersas no ar, e o índice de refração do
material da fibra (nlente = 1,5) é maior que o do meio (nar = 1), a microlente tem
vergência positiva. Logo, a microlente é convergente.
Resposta
da
questão
95:
[D]
Dados obtidos a partir da leitura do gráfico:
ri = 3 10–10 m Ui = 3 10–18 J;
rf = 9 10–10 m Uf = 1 10–18 J.
Como a força elétrica (força conservativa), nesse caso, é a própria força resultante,
podemos combinar os Teoremas da Energia Potencial (TEP) e da Energia Cinética
(TEC).
Página 126 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
τFconservativa ΔU
τFresultante ΔEcin
ΔEcin ΔU
ΔEcin Uf Ui 1 3 1018
ΔEcin 2 1018 J.
Ecin > 0 a energia cinética aumenta.
Resposta
da
questão
96:
[C]
A quantidade de carga elétrica contida na bateria é dada por:
q i Δt
75Ah 50A Δt
75
Δt
h
50
Δt 1,5h
Sabendo que a autonomia (em horas) da bateria é 1,5 horas temos:
Δs v Δt
Δs 60 1,5
Δs 90 km
Resposta
da
questão
97:
[B]
Como o circuito está aberto entre os pontos A e B, a corrente elétrica entre esses pontos
é nula, sendo, portanto, também nula a corrente pelo resistor de R2 = 4 , ligado ao
ponto A; ou seja, esse resistor não tem função, não entrando no cálculo da resistência
equivalente. O circuito da figura 2 é uma simplificação do circuito da figura 1.
Página 127 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Calculando a resistência equivalente:
Req
2
4 5 .
2
A ddp no trecho é U = 5 V, e a ddp entre os pontos A e B (UAB) é a própria ddp no
resistor R1. Assim:
U Req I I
U
5
1 A.
Req 5
UAB R1 i 4 1 UAB 4 V.
Resposta
da
questão
98:
a) Aplicando a 1ª Lei de Ohm na 2ª e 4ª linhas:
V
V R I I
R
1,1
I2 4,4 0,25 A.
I 0,96 0,60 A.
4
1,6
Página 128 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
V(V) R( ) I(A)
1,14
7,55
0,15
1,10
4,40
0,25
1,05
2,62
0,40
0,96
1,60
0,60
0,85
0,94
0,90
b) Substituindo os valores da tabela do item anterior:
Obs.: no eixo das tensões, os valores começam a partir de V = 0,7 V, por isso a reta não
cruza o eixo das correntes no valor da corrente de curto circuito.
c) Substituindo os dois primeiros valores de V e de I da tabela na equação do gerador e
subtraindo membro a membro as duas equações:
1,14 ε r 0,15
V ε r I 1,10 ε r 0,25
0,04 0 0,10 r
1,14 ε 0,4 0,15
r
0,04
r 0,4 Ω.
0,1
ε 1,14 0,06 ε 1,2 V.
Obs.: A equação dessa bateria é:
V 1,2 0,4 I.
Para V = 0,7 V:
0,7 1,2 0,4 I I
1,2 0,7
0,4
i 1,25 A.
Página 129 de 130
LISTA DE EXERCÍCIOS 1 – FUVEST/UNICAMP – 3ª SÉRIE
Esse é o valor em que a linha do gráfico corta o eixo das correntes, como assinalado no
gráfico do item anterior.
Resposta
da
questão
99:
a) Dados: c = 3 10 m/s; f = 60 Hz.
8
Da equação fundamental da ondulatória:
cλ f λ
c 3 108
f
60
λ 5 106 m.
b) Dados: P = 400 MW = 400 106 W; U = 500 kV = 500 103 V.
Da expressão da potência elétrica:
PU i i
Resposta
P 400 106
U 500 103
da
i 800 A.
questão
100:
[C]
Dados: U = 100 106 V; Q = 10 C; 1 J = 3 10-7 kWh.
kW h
ΔE U Q 100 106 10 109 J ΔE 109 J 3 107
.
J
ΔE 300 kW h.
Página 130 de 130