Melhor caminho entre duas estações de metro

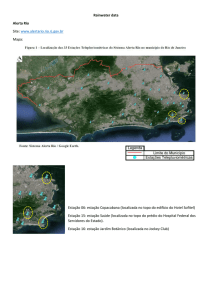
Faculdade de Engenharia da Universidade do Porto
Mestrado Integrado em Engenharia Informática e Computação
Melhor caminho entre duas estações de metro
Relatório do Trabalho Prático de CPAL 2008/2009
João Carlos Figueiredo Rodrigues Prudêncio
Seraphin Rodrigues Miranda
Turma 6
14 de Maio de 2009
Melhor caminho entre duas estações de metro
1
Declaração de originalidade
Os autores declaram que o relatório e código fonte submetido é da sua autoria, excepto
nas partes explicitamente assinaladas com referência à respectiva fonte. A utilização de
uma fonte não referenciada implica a anulação do trabalho.
Melhor caminho entre duas estações de metro
2
1 Introdução
Este relatório descreve o trabalho realizado na disciplina de CPAL, o qual teve como
objectivo o desenvolvimento de um programa em Java para determinar qual o melhor
caminho entre duas estações de metro.
Para a elaboração do trabalho acima descrito será necessário responder aos seguintes
requisitos:
• A configuração das linhas de metro deverá ser definida num ficheiro de texto;
• Na escolha do melhor caminho entre duas estações deverá ter-se em conta, em
primeiro lugar, a minimização das mudanças de linha de circulação e em segundo
lugar a minimização do número de estações atravessadas.
• No caso de haver dois caminhos igualmente bons, por esses critérios acima
descritos, o programa poderá escolher qualquer um desses caminhos.
• O programa deverá funcionar consoante os parâmetros de chamada.
Necessariamente deverá ser passado como primeiro parâmetro, o nome do ficheiro
com a configuração da rede. Para além do nome do ficheiro poderá, opcionalmente,
ser passado a estação de origem, ou ainda, a estação de origem e a estação de
destino. Consoante as entradas o programa deverá escrever no standard output a
respectiva solução.
o No caso de serem inseridos os três argumentos (nome do ficheiro de texto,
estação de origem e estação de destino) o programa deverá escrever no
standard output o melhor caminho entre as estações indicadas.
o No caso de serem inseridos os dois argumentos (nome do ficheiro e a estação
de origem) o programa deverá escrever no standard output os melhores
caminhos entre a estação de origem e todas as outras estações.
o No caso de ser inserido apenas o nome do ficheiro, o programa deverá
escrever no standard output os melhores caminhos entre todos os pares de
estações.
• Opcionalmente poderá ser desenvolvido uma interface gráfica, para o programa, de
modo a facilitar a interacção do programa com o utilizador.
Melhor caminho entre duas estações de metro
3
2 Desenvolvimento
2.1
Algoritmos e estruturas de dados
Para a elaboração deste projecto o conhecimento de alguns conceitos e
algoritmos é essencial.
Grafo é o objecto básico de estudo da teoria dos grafos. É representado como um
conjunto de vértices ligados por arestas.
Figura 1 – Um grafo com 6 aresta e 7 vértices
Os grafos são usados correntemente em muitos problemas da vida real. Uma
dessas utilizações é encontrar o caminho mais curto entre dois locais ( dois vértices ). O
algoritmo de Dijkstra, inventado pelo cientista da computação Edsger Dijkstra,
resolve esse problema em tempo computacional O([m+n]log n) onde m é o número de
arestas e n é o número de vértices.
•
Algoritmo de Dijkstra
o 1º passo: iniciar valores
para todo v ∈ V[G]
d[v]← ∞
π[v] ← nulo
d[s] ← 0
V[G] é o conjunto de vértices(v) que formam o Grafo G. d[v] é o vector de
distâncias de s até cada v. π[v] identifica o vértice de onde se origina uma
conexão até v de maneira a formar um caminho mínimo.
o 2º passo: usam-se dois conjuntos: S, que representa todos os vértices v onde
d[v] já contem o custo do menor caminho e Q que contem todos os outros
vértices.
o 3º passo:
enquanto Q ≠ ø
u ← extraia-mín(Q)
Melhor caminho entre duas estações de metro
4
S ← S ∪ {u}
para cada v adjacente a u
se d[v] > d[u] + w(u, v)
então d[v] ← d[u] + w(u, v)
π[v] ← u
w(u, v) é o peso(weight) da aresta que vai de u a v.
u e v são vértices quaisquer e s é o vértice inicial.
extrai-mín(Q), pode ser um heap de mínimo ou uma lista ordenada de vértices
onde obtém-se o menor elemento, ou qualquer estrutura do tipo.
No final do algoritmo teremos o menor caminho entre s e qualquer outro vértice
de G.
•
Priority Queue
O algoritmo para encontrar o caminho mais curto acima descrito, necessita de
uma fila de prioridade. A API do java já disponibiliza uma mas que não é eficiente
para este método, resolvemos portanto usar outra que foi leccionada numa das aulas
práticas da disciplina. Esta estrutura está baseada num heap mínimo. Existem dois
tipos de heaps: Os heaps de máximo (max heap), em que o valor de todos os nós são
menores que os de seus respectivos pais; e os heaps de mínimo (min heap), em que
o valor todos os nós são maiores que os de seus respectivos pais. Assim, em um
heap máximo, o maior valor do conjunto está na raiz da árvore, enquanto no heap de
mínimo a raiz armazena o menor valor existente.
Irão existir um conjunto de métodos que vão alterando as prioridades do conjunto de
elementos, garantindo sempre que na cabeça do heap se encontro o valor mínimo.
•
Eficiência do algoritmo de Dijkstra:
Tempo de execução é O(|V| + |E| + |V| log|V| + |E| log |V|), ou simplesmente
O(|E| log |V|) se |E|>|V|.
O( |V| log |V|) - extracção e inserção na fila de prioridades. O número de
extracções e inserções é |V|.
Cada operação destas pode ser feita em tempo “logarítmico” no tamanho da fila, que no
máximo é |V|.
O( |E| log |V|) – decreaseKey
Feito no máximo |E| vezes (uma vez por cada aresta)
Cada operação destas pode ser feita em tempo “logarítmico” no tamanho da
fila, que no máximo é |V|.
Melhor caminho entre duas estações de metro
2.2
Estrutura de classes
Figura 2 – Diagrama de classes em UML
Principais bibliotecas utilizadas:
o java.io.IOException;
o java.util.LinkedList;
o java.io.BufferedInputStream;
o java.io.DataInputStream;
o java.io.File;
o java.io.FileInputStream;
o java.io.IOException;
o java.io.Serializable;
o java.util.ArrayList;
o java.util.Iterator;
5
Melhor caminho entre duas estações de metro
6
Estas bibliotecas foram importadas para o uso de contentores, para a leitura e
escrita de dados em ficheiros de texto, para o uso de excepções.
As classes necessárias para o desenvolvimento da aplicação foram:
o Vértice;
o Aresta;
o Grafo;
o MyPriorityQueue;
As classes Vértice, Aresta e Grafo foram definidas com base nos slides de CPAL
(grafos1a.pdf – slide 11). A classe MyProirityQueue também foi retirado de uma das
aulas de CPAL.
No desenho do diagrama de classes verificou-se que não houve necessidade de
usar o conceito de herança, também não tivemos a necessidade de usar polimorfismo. O
uso do encapsulamento foi diminuto dado que para resolver o problema foram
necessárias poucas classes.
2.3 Interface gráfica (opcional)
1. Opção para abrir o ficheiro que contém a configuração das linhas
2. Menu que permite escolher o ficheiro e a sua localização, só admite abertura de ficheiro com extensão .txt
Melhor caminho entre duas estações de metro
7
3. Escolha do caminho baseado nas escolhas e desenho do respectivo caminho em modo de texto e em modo gráfico
4. Permite guardar os resultados num ficheiro de texto para futura visualização
5. Consulta do menu de ajuda com explicação do funcionamento da aplicação
Dada a simplicidade do interface gráfica pode resumir-se a sua elaboração através das
seguintes principais componentes:
o JPanel;
o JButton;
o jComboBox;
o jFileChooser;
o JMenuItem;
O principal evento foi o MouseClicked dado que interface funciona a base de clicks.
Na realização da interface gráfica, no desenho do grafo em modo gráfico, foi usado
a toolkit PREFUSE obtida do site http://prefuse.org/ a qual adaptamos ao nosso
projecto.
Melhor caminho entre duas estações de metro
8
3 Utilização
Dado que criamos uma interface gráfica para a nossa aplicação tornamos esta
aplicação fácil de manusear. A utilização da aplicação pode ser detalhada em
poucas etapas:
1- Abrir o executável.
2- Opção File -> Open.
3- Escolher o ficheiro que contém as configurações das linhas.
4- Carregar no botão Abrir.
5- Escolher as linhas dos campos FROM e TO.
a. No caso de não serem escolhidas estações dos campos FROM e TO
serão calculados todos os melhores caminhos entre todas as estações.
b. No caso de ser escolhidas apenas uma estação do campo FROM, a
aplicação irá calcular todos os melhores caminhos entre a estação do
campo FROM entre todas as restantes.
c. No caso de serem escolhidas os dois campos será calculado o melhor
caminho entre as duas estações.
6- Após as escolhas, deverá carregar no botão calcular que apresentará os
resultados em modo texto e também em modo gráfico.
7- No fim terá a possibilidade de guardar o caminho calculado em modo texto num
ficheiro de texto, usando a opção Save do menu File.
8- Poderá sair da aplicação recorrendo ao menu File -> opção Exit.
O ficheiro de entrada deve seguir a seguinte estrutura:
6
A16578
B1241
C5412
D3174
E8259
F9415
6 -> número de linhas
A 1 6 5 7 8 -> linha A com a estação 1 que liga a estação 6, com estação 6 que
liga a estação 5, com estação 5 que liga a estação 7 e com estação 7 que liga a
estação 8. O mesmo acontece para as restantes linhas.
A saída para o ficheiro seguirá a seguinte estrutura:
1A6
1 A 6 –> caminho que passa pela estação 1 para a estação 6 através da linha A.
Melhor caminho entre duas estações de metro
4
9
Testes
Foram elaborados um conjunto de testes ao nosso programa para assegurar que
este cumpria os requisitos pretendidos. Para tal usamos a ferramenta JUnit que nos
disponibiliza algumas funções úteis para testarmos o nosso programa. Inicialmente
começamos por testar as funcionalidades básicas, tais como criar arestas, vértices e
grafos. Posteriormente procedemos a testes relativos ao algoritmo para determinar o
caminho mais curto.
Usamos vários grafos de teste, variando a sua dimensão e complexidade para nos
certificarmos se o algoritmo estava a funcionar correctamente. Após alguns testes
consideramos razoável aceitar que o algoritmo não tinha falhas.
Relativamente à complexidade temporal elaboramos também um teste ao tempo
de execução do programa. Os resultados foram sempre valores residuais e que variavam
consoante o computador que estivessemos a usar.
Uma lista extensiva destes testes pode ser encontrada no ficheiro "testes.java".
5 Conclusões
Métricas:
- LOC:
a) Total: cerca de 2500 linhas
b) Original: 2400 linhas
c) Reutilizado: 100 linhas
- Horas gastas:
a) João Prudêncio: 31 horas
b) Seraphin Miranda: 31 horas
Todas as especificações e requisitos foram cumpridos incluindo o desenvolvimento
da interface gráfica opcional. Não foi encontrado até a data qualquer problema com
a nossa aplicação.
6 Referências
•
•
•
http://paginas.fe.up.pt/~nflores/dokuwiki/lib/exe/fetch.php?id=teaching%3A0809%
3Acpal&cache=cache&media=teaching:0809:cpal:grafos2b.pdf - Algoritmo de
Dijkstra.
http://paginas.fe.up.pt/~nflores/dokuwiki/lib/exe/fetch.php?id=teaching%3A0809%
3Acpal&cache=cache&media=teaching:0809:cpal:grafos1a.pdf - Definições base de
Vértice, Aresta e Grafo.
http://prefuse.org/ - toolkit para desenho gráfico da linhas e estações com a
respectiva solução do problema.