1aLista de Exercícios - Cinemática em 1 dimensão

1 Lista de Exercícios - Cinemática em 1 dimensão
a
1. (Halliday1 25E) O gráfico abaixo representa o movimento de uma partícula ao longo do
eixo-x. Faça um esboço dos gráficos correspondentes para a velocidade e a aceleração.
2. (Halliday 29E) A posição de uma partícula é dada pela função: x(t) = 20t − 5t3 , sendo
x em metros e t em segundos. (a) Quando, se ocorrer, a velocidade da particula e
nula?, (b) Quando a aceleração é nula?, (c) Quando a aceleração é positiva e quando
é negativa? (assuma que a lei do movimento é valida para t < 0) (d) Trace os gráficos
a(t), v(t) e x(t).
[Respostas: a) t = ±1.15 s; b) t = 0; c) a > 0 se t < 0 e a < 0 se t > 0]
3. (Halliday 47P) Um trem parte do repouso e se move com aceleração constante. Em um
determinado instante ele viaja a 30 m/s e 160 m adiante trafega a 50 m/s. Calcule:
(a) sua aceleração, (b) o tempo necessário para percorrer os 160 m mencionados, (c) o
tempo necessário para atingir a velocidade de 30 m/s, (d) a distância percorrida desde
o repouso até ele atingir a velocidade de 30 m/s. (e) Faça os gráficos v(t) e x(t), a
partir do ponto de repouso.
[Respostas: a) 5 m/s2 ; b) 4 s; c) 6 s; d) 90 m]
4. (Halliday 52P) Quando um motorista para um carro tão rapidamente quanto possível,
a distância percorrida até o carro parar é a soma da “distância de reação”, Dr , com a
“distância de frenagem”, Df . A primeira corresponde à velocidade inicial, v0 , multiplicada pelo tempo de reação do motorista. A segunda é a distância percorrida pelo carro
enquanto está freando. A tabela abaixo, mostra valores típicos destas quantidades para
algumas velocidades iniciais. Pede-se: (a) qual o tempo de reação do motorista? (b)
se a velocidade inicial do carro fosse 25 m/s, qual seria distância total percorrida até
o carro parar?
v0 (m/s) Dr (m) Df (m) Dtotal (m)
10
7,5
5,0
12,5
20
15
20
35
30
22,5
45
67,5
[Respostas: a) 0.75 s; b) 50 m]
5. (Halliday 65E) Um modelo de foguete propelido por queima de combustível decola
verticalmente com aceleração a constante, partindo do repouso. Quando é decorrido
um intervalo de tempo T , o combustível acaba e o foguete entra em queda livre. Trace
qualitativamente (não são necessários valores numéricos) os gráficos y(t), v(t) e a(t).
1
Halliday significa a 4a edição de Fundamentos de Física - vol I, de Halliday, Resnick e Walker.
1
6. (Halliday 73P) Uma pedra é atirada verticalmente para baixo, de uma altura H, com
velocidade inicial de módulo u. (a) Qual será sua velocidade no instante em que tocar
no solo? (b) Quanto tempo a pedra levará para chegar ao solo? (c) Quais seriam as
respostas para os ítens (a) e (b) se a pedra fosse lançada com a mesma velocidade
para cima? Antes de fazer qualquer cálculo, responda se cada uma das respostas será
maior, menor ou igual à da questão original
[Respostas: a) v = − u2 + 2gH; b) t =
u2 + 2gH − u /g; c) v não muda, t =
u2 + 2gH + u /g]
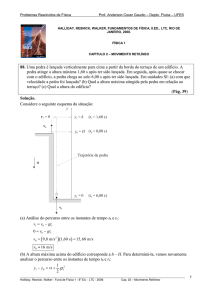
7. (Halliday 71P) No National Physical Laboratory, na Inglaterra, foi realizada uma medida
da aceleração da gravidade, g, atirando-se uma bola de vidro para cima no interior de
um tubo onde se fez vácuo. Na figura abaixo, que representa graficamente a posição
da bola em função do tempo, consideremos ∆Ts o intervalo de tempo decorrido entre
as duas passagens da bola pelo nível superior e ∆Ti o intervalo entre as duas passagens
pelo nível inferior. Sabendo-se que a distância entre estes dois níveis é H, mostre que
g=
8H
− ∆Ts2
∆Ti2
8. (Halliday 96) Uma pedra é lançada verticalmente para cima do topo de um edifício muito
alto. A pedra alcança a altura máxima, acima do prédio, 1,60 s após o lançamento.
A seguir, ela passa junto à borda do prédio, chocando-se com o solo 6,00 s após ter
sido lançada. Calcule em unidades SI: (a) com que velocidade inicial foi lançada, (b)
que altura máxima acima do prédio a pedra alcançou e (c) qual a altura do prédio.
[Respostas: a) 15.7 m/s; b) 12.6 m; c) 82.4 m]
∆T
T S
x(t)
s
H
t
Tl ∆T
Problema 1
I
Problema 7
2