O que é capacitor?

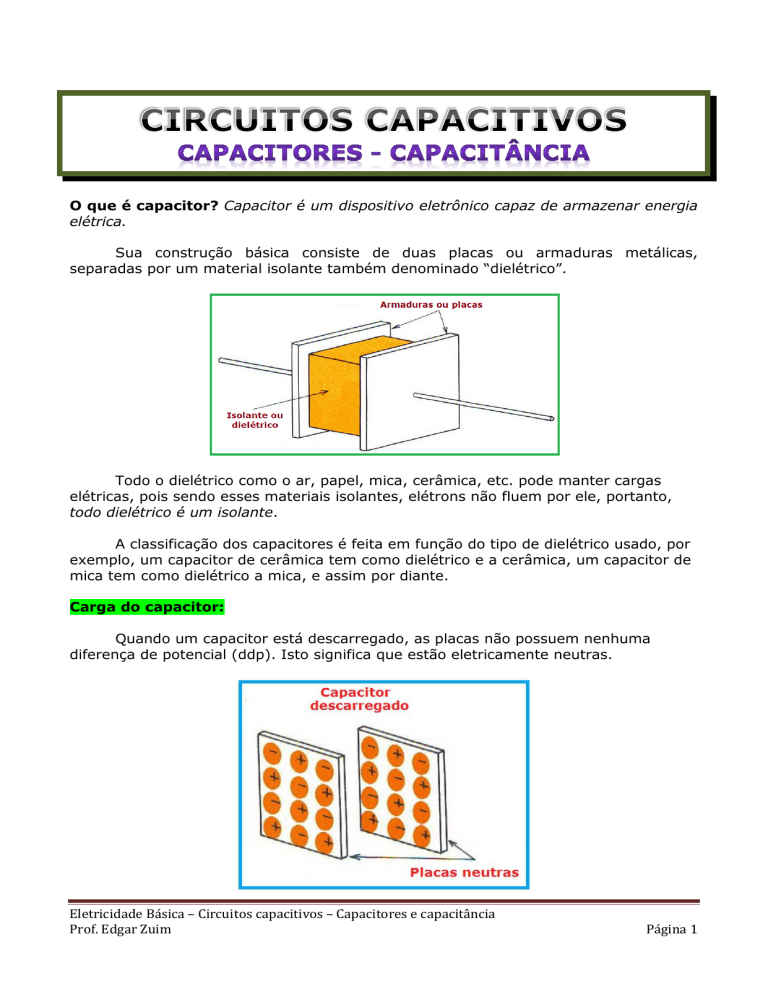
O que é capacitor? Capacitor é um dispositivo eletrônico capaz de armazenar energia
elétrica.
Sua construção básica consiste de duas placas ou armaduras metálicas,
separadas por um material isolante também denominado “dielétrico”.
Todo o dielétrico como o ar, papel, mica, cerâmica, etc. pode manter cargas
elétricas, pois sendo esses materiais isolantes, elétrons não fluem por ele, portanto,
todo dielétrico é um isolante.
A classificação dos capacitores é feita em função do tipo de dielétrico usado, por
exemplo, um capacitor de cerâmica tem como dielétrico e a cerâmica, um capacitor de
mica tem como dielétrico a mica, e assim por diante.
Carga do capacitor:
Quando um capacitor está descarregado, as placas não possuem nenhuma
diferença de potencial (ddp). Isto significa que estão eletricamente neutras.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 1
Quando um capacitor é carregado, uma placa recebe excesso de elétrons
tornando-se eletrizada negativamente, enquanto que na outra elétrons são removidos,
tornando-se eletrizada positivamente.
Entre as duas placas existirá então uma ddp. No exemplo ilustrado na figura
acima, o dielétrico é o ar.
Simbologia:
Veja na figura abaixo as simbologias mais conhecidas para a representação de
capacitores.
Armazenando cargas em um capacitor:
Para armazenar cargas em um capacitor, é preciso que no mesmo seja aplicada
uma tensão.
A figura a seguir mostra um circuito básico, onde um capacitor é submetido a
uma tensão DC.
No momento em que a chave Sw é fechada, ocorrerá uma diferença de potencial
entre as placas do mesmo pela ação da bateria.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 2
1. Quando a chave Sw é fechada, os elétrons do terminal negativo da bateria se
acumulam na placa inferior, pois a mesma está ligada ao terminal negativo da bateria.
2. Enquanto isso a placa superior perde elétrons ficando então positiva (falta de
elétrons). Nessa condição cria-se um campo eletrostático entre as duas placas e a
placa inferior tende a repelir os elétrons da placa superior.
3. Se por exemplo, na placa inferior forem acumulados 6,25 . 1018 elétrons, então, o
capacitor estará com uma carga de 1 coulomb.
4. Podemos levar em consideração os elétrons acumulados em apenas uma das placas
para efeito de carga adquirida uma vez que, a quantidade de elétrons acumulados em
uma das placas é a mesma tomada da outra placa.
5. Logo, se em uma das placas existirem 6,25 . 1018 elétrons, na outra faltará a
mesma quantidade de elétrons, ou seja, 6,25 . 1018 elétrons.
6. Isso se explica pois o campo eletrostático (campo elétrico) formado pelos elétrons
em uma das placas, repele os elétrons da outra placa.
Portanto, quanto mais carregado estiver o capacitor, maior será esse campo
elétrico.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 3
Carga de um capacitor num circuito DC:
Inicialmente, quando Sw estiver aberta, nenhuma corrente circulará pelo
circuito, pois não há ddp nos terminais do capacitor.
Quando Sw for fechada a corrente no circuito será instantânea e irá diminuindo
até se tornar nula, pois o capacitor inicialmente descarregado se encarregará de
redistribuir as cargas elétricas pelo circuito.
Depois de um tempo, não haverá mais corrente pelo circuito. O capacitor
bloqueia totalmente a passagem de DC.
“Quanto maior for a valor da capacitância do capacitor, maior será a corrente
inicial no circuito”.
Observe no gráfico que quando Sw for fechada o valor da corrente no circuito é
máximo, sendo a corrente limitada apenas pela resistência do circuito (resistência do
fio e até a própria resistência interna da fonte ou também, de uma resistência
externa).
Quando a chave Sw for aberta, o capacitor se manterá carregado com a tensão
que lhe foi aplicada.
Resumindo: “Quando o capacitor estiver totalmente carregado, nenhuma
corrente fluirá pelo circuito”.
Podemos então afirmar que o capacitor bloqueia corrente contínua.
Quando o capacitor está se carregando, a corrente que flui pelo circuito é
denominada corrente de carga. À medida que essa corrente diminui, a tensão sobre o
capacitor aumenta tendendo a se opor à tensão de entrada.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 4
Descarga do capacitor:
Quando o capacitor está carregado, teoricamente sua carga será mantida
indefinidamente, a não ser que seja provoca a descarga entre suas placas por um meio
qualquer.
Na prática quando um capacitor é removido da fonte de carga, uma série de
fatores, como por exemplo, a própria resistência interna (fuga) do capacitor não
permite que essa carga seja mantida indefinidamente.
“Qualquer meio condutor entre as duas placas de um capacitor totalmente
carregado provocará a anulação da ddp entre as duas placas. A isto
denominamos descarga do capacitor”.
A figura acima ilustra o processo de carga e descarga de um capacitor. Observe
o acionamento da chave Sw2 durante o processo de descarga.
Fechando Sw2, ocorre a anulação da ddp entre as mesmas.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 5
UNIDADE DE CAPACITÂNCIA
A capacitância é a quantidade de carga que um capacitor pode armazenar.
É importante lembrar que, quando falamos de carga armazenada em um
capacitor, essa carga refere-se a uma das placas, porquanto as mesmas possuem o
mesmo valor, porém, com polaridades opostas.
A unidade de medida da capacitância é o farad, em homenagem ao físico e
químico inglês Michael Faraday (1791-1867).
O que é o farad?
O farad é uma unidade de capacidade elétrica equivalente a um capacitor em
cujas placas aparece uma diferença de potencial de 1 volt, quando ele é carregado com
uma quantidade de eletricidade equivalente a 1 coulomb.
A carga armazenada pode ser calculada pela fórmula:
Q = C.V
Onde:
Q = carga armazenada, em coulombs
C = capacitância em farads
V = tensão em volts
Como a unidade “farad” é muito grande, costuma-se utilizar os submúltiplos
para os capacitores utilizados em circuitos eletrônicos.
Assim, temos:
farad (F) = unidade
milifarad (mF) = milésima parte do farad (10-3)
microfarad (µF) = milionésima parte do farad (10-6)
nanofarad (nF) = bilionésima parte do farad (10-9)
picofarad = trilionésima parte do farad (10-12)
O submúltiplo milifarad (10-3) raramente é usado em capacitores convencionais
para circuitos eletrônicos.
Exemplos:
1. Qual é a carga adquirida por um capacitor de 2µF quando submetido a uma tensão
de 200 volts?
Q = C.E
Q = 2µF x 200V = 400µC (microcoulomb)
ou
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 6
400 x 10-6 C
2. Um capacitor quando submetido a uma tensão de 1.000 volts, armazena 0,05C.
Qual é a capacitância do mesmo?
Q = C.E, logo, C = Q/E
C = 0,05C / 1.000 volts
C = 0,00005F ou 50µF
3. Um capacitor de 100µF ao ser submetido a uma determinada tensão adquiriu uma
carga de 0,0015C. A que tensão o mesmo foi submetido?
Q = C.E, logo, E = Q/C
E = 0,0015C / 0,0001F = 15 volts
CONTANTE DE TEMPO CAPACITIVA
Quando um capacitor é ligado a uma fonte DC, se não houver nenhuma
resistência, carrega-se totalmente quase que instantaneamente.
Quando no circuito houver uma resistência (do próprio fio, resistência interna da
fonte ou até mesmo uma resistência externa) haverá um tempo de atraso para que o
capacitor atinja a carga total, que é o produto da capacitância pela resistência,
conhecido como constante de tempo.
τ = R.C
τ = tempo em segundos
R = resistência em ohms
C = capacitância em farads
Tomemos como exemplo o circuito abaixo:
Quando Sw for fechada, circulará uma corrente máxima pelo circuito que vai
diminuindo até que o capacitor se carregue com a tensão da fonte.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 7
Esse tempo de carga é dado pela constante de tempo: τ = R.C
τ = 1.106 x 1.10-6 = 1 segundo
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 8
Interpretando a constante de tempo:
Analisando o gráfico referente a carga do capacitor no circuito, que representa o
aumento da tensão sobre o mesmo, concluímos:
1. A constante de tempo do circuito é de 1 segundo (1s).
2. Em 1 segundo a tensão sobre o capacitor será igual a 63,2% da tensão da fonte, ou
seja, 6,32 volts.
3. Em 2 segundos, que equivale a 2 constantes de tempo, a tensão sobre o capacitor
será de 86,4% da tensão da fonte, ou seja, 8,64 volts.
4. De forma análoga, em 3 constantes de tempo, o capacitor se carregará com 9,49
volts e em 4 constantes de tempo e capacitor estará carregado com 9,81 volts.
5. A carga total do capacitor ocorrerá somente após 5 constantes de tempo, ou seja, 5
segundos, com 9,99 volts, arredondando: 10 volts.
A constante de tempo para a descarga obedece ao mesmo procedimento de
cálculo.
Tomemos como exemplo o circuito abaixo:
1. Quando Sw é posicionada em “a”, o capacitor carrega-se com a tensão da
fonte através do resistor de 100k.
2. Com Sw em “c” o capacitor mantém a sua carga.
3. Ligando Sw em “b” o capacitor descarrega-se através do resistor de 100k.
Como os valores dos resistores para carga e descarga são iguais, a constante de
tempo será igual tanto para a carga como para a descarga do capacitor.
τ = R.C
τ = 100.103 x 5.10-6 = 0,5s (meio segundo)
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 9
Portanto:
a) em meio segundo (0,5s) o capacitor estará carregado com 6,32 volts
b) no processo de descarga, em meio segundo (0,5s), a tensão remanescente no
capacitor será de 3,68 volts.
c) o processo de carga e descarga do capacitor será de 5 constantes de tempo, o
que equivale a 2,5 segundos.
Veja o gráfico abaixo referente ao processo de descarga do capacitor com
respectivos percentuais, para 5 constantes de tempo.
FATORES QUE DETERMINAM A CAPACITÂNCIA
Na fabricação de um capacitor 3 fatores primordiais devem ser levados em
conta, para definir a sua capacitância:
1. Área das placas: Quanto maior for a área das placas, maior será a capacitância. É
fácil imaginar que um capacitor com área de placa maior, armazenará mais energia.
2. Tipo de dielétrico: Quanto maior for a constante dielétrica do dielétrico, maior será
a capacitância.
A constante dielétrica é representada pela letra “k”. O ar ou vácuo é utilizado
como referencial para a constante dielétrica, onde k= 1.
A tabela a seguir mostra a constante dielétrica de alguns dielétricos.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 10
DIELÉTRICO
Vácuo
Ar
Baquelite
Fibra
Vidro
Mica
Cerâmica
Óleo
Papel
Porcelana
Parafina
Quartzo
Borracha
Água (20ºC)
k
1,0000(ref)
1,00058986
4 a 8,5
5,5
8
3a6
80 a 1.200
2a5
2a6
4a6
2,5
4,5 a 5
3 a 35
80,1
Se analisarmos a tabela acima, um capacitor com dielétrico de vidro tem uma
capacidade de armazenamento 8 vezes maior do que o dielétrico a ar, levando-se em
conta as características físicas iguais para os dois tipos de capacitores.
3. Distância entre as placas: A distância entre as placas é determinada pela
espessura do dielétrico. Quanto mais fino o dielétrico, maior será a capacitância.
Existe outro fator importante na definição da capacitância que é a quantidade
de placas.
É o caso dos capacitores usados na sintonia de estações de rádio, compostos de
várias placas, cujo dielétrico normalmente é o ar. São os capacitores variáveis.
A figura a seguir ilustra um capacitor variável com múltiplas placas para uso
geral.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 11
A tecnologia de múltiplas placas em capacitores, que na realidade representa
multicamadas, é muito utilizada quando se deseja capacitores para altas tensões de
trabalho.
CÁLCULO DA CAPACITÂNCIA
plano.
Através da fórmula a seguir pode-se calcular a capacitância de um capacitor
Onde:
C = capacitância em picofarad (10-12)
0,0885 = constante eletrônica
A = área da superfície das placas em centímetros quadrados
d = distância entre as placas, em centímetros (espessura do dielétrico)
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 12
N = número de placas
Observe que a fórmula usada para o cálculo da capacitância foi convertida para o
sistema CGS (do SI para o CGS), daí então a área das placas ser especificada em
centímetros quadrados e a distância em centímetros.
Dessa forma, o resultado deverá ser expresso em picofarad.
OBS: a constante eletrônica 0,0885 é a permissividade elétrica no vácuo, que
corresponde no SI a:
Para melhor entendimento, alguns exemplos a seguir:
1. Qual é a capacitância de um capacitor de 2 placas quadradas, sendo que cada placa
mede 0,5cm de lado, cujo dielétrico é a cerâmica (k=1.200) e a espessura do dielétrico
é 0,3mm.
Solução:
0,5cm de lado para cada placa quadrada, teremos uma área de 0,25cm2
0,3mm = 0,03cm.
C = 0,0885 . 1200 . 0,25 . (2-1) / 0,03
C = 26,55 / 0,03 = 885pF
Resolvendo o mesmo exercício no SI:
Lembrando que:
a) a área é dada em metros quadrados
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 13
b) a distância é dada em metros
c) a unidade de medida em farads (F)
 0,5cm = 0,005 metros
 0,3mm = 0,0003 metros
d) o resultado: 8,85 . 10-10 F é a mesma coisa do que 885pF ou 885 . 10-12F
2. Qual é a capacitância de um capacitor plano formado por duas placas de 18cm x
18cm, com dielétrico de vidro com espessura de 2mm?
Solução:
18cm x 18cm = 324cm2 = área de cada placa
2mm = 0,2cm
K = 8 (conforme tabela)
C = 0,0885 . 324 . 8 . (2-1) / 0,2
C = 229,392 / 0,2 = 1.146,96pF
Resolvendo o mesmo exercício no SI:
18cm = 0,18m (0,18m)2 = 0,0324m2
2mm de espessura equivale a 0,002m
OBS: 1,147 . 10-9 F é a mesma coisa do que 1,147nF ou 1.147pF
ou
0,001147µF
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 14
Quando um capacitor é ligado a uma fonte AC, alternadamente ele se carrega e
descarrega, com sentidos opostos.
A figura a seguir ilustra o processo de carga e descarga do capacitor quando
submetido a uma tensão AC.
A cada meio ciclo o capacitor carrega-se e descarrega-se. Como cada um dos
semiciclos tem suas polaridades invertidas, ocorre a carga e descarga em um sentido e
depois em outro sentido.
Vamos analisar o que ocorre nos semiciclo positivo e negativo:
1. de 0 a 90º o capacitor carrega-se positivamente.
2. de 90º a 180º o capacitor começa a se descarregar, porém não muda de
polaridade, que é positiva.
3. de 180º a 270º o capacitor começa a carregar-se novamente porém com
sentido oposto.
4. de 270º a 360º o capacitor começa a se descarregar, porém não muda de
polaridade, que agora é negativa.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 15
Relação entre as tensões:
Observe na figura mostrada anteriormente o sentido das correntes no processo
de carga e descarga do capacitor durante um ciclo.
a) no processo de carga (0 a 90º) e no processo de descarga (270 a 360º) o
sentido da corrente é o mesmo.
b) no processo de descarga (90 a 180º) e no processo de carga no sentido
negativo (180 a 270º) o sentido de corrente também é o mesmo.
Vamos considerar, por exemplo, o que ocorre entre 90º e 270º:
 de 90 a 180º o capacitor começa o processo de descarga. O capacitor
descarrega totalmente quando a tensão aplicada cai a zero (180º) e começa a
carregar-se no mesmo sentido no qual estava se descarregando anteriormente.
 conclui-se então que existe uma corrente AC circulando pelo circuito
continuadamente. Logo, um capacitor permite a passagem de corrente AC.
 a acumulação de cargas nas placas do capacitor, varia senoidalmente
acompanhando a tensão aplicada.
 em virtude disso no capacitor é desenvolvida uma contratensão que está
defasada 180º em relação à tensão aplicada.
Relação entre a tensão e a corrente:
Quando uma fonte de tensão AC é ligada aos terminais de um capacitor, a
corrente no circuito é máxima, no instante em que a tensão da fonte, senoidalmente
começa a crescer a partir do zero.
Isso é explicável, pois um capacitor completamente descarregado atua como um
“curto” no instante em que a fonte é ligada, e à medida que as placas vão se
carregando, as placas começam a apresentar uma oposição à corrente.
Quando a tensão alcança o seu valor de pico, o capacitor estará carregado
apresentando assim uma oposição à passagem da corrente de maneira a cancelar o
fluxo da mesma.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 16
Conforme podemos verificar na figura a seguir, a relação de fase entre a tensão
e a corrente é de 90º, estando a corrente adiantada em relação à tensão aplicada.
O gráfico a seguir ilustra as defasagens entre corrente, tensão aplicada e
contratensão.
CONCLUINDO: A corrente através do capacitor está defasada 90º tanto em
relação à tensão aplicada como em relação à contratensão. A corrente está adiantada
90º em relação à tensão aplicada e atrasada 90º em relação à contratensão.
O efeito da frequência e capacitância na corrente do capacitor:
Quando uma tensão AC é aplicada em um capacitor, este se carrega e se
descarrega alternadamente (em ambos os sentidos) durante cada ciclo da tensão
aplicada.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 17
A intensidade do fluxo de elétrons (corrente) é determinada pela quantidade de
elétrons que passa por um ponto do circuito em um determinado tempo unitário (no SI
esse tempo é igual a 1 segundo).
Em outras palavras a corrente á igual a taxa do fluxo de elétrons sendo expressa
pela equação:
I=Q/t
I = corrente em ampères
Q = carga em coulomb
t = tempo em segundos
A carga e descarga do capacitor em AC acompanham exatamente as variações
de tensão desde o seu valor zero até o seu valor de pico, pouco importando a
frequência.
Assim, se tivermos dois capacitores iguais ligados a uma fonte de tensão com
amplitudes iguais, mas, de frequências diferentes, os valores de Q serão iguais, porém
os valores da corrente serão diferentes, devido aos valores de “t” serem diferentes,
lembrando que “t” é o período do ciclo.
Resumindo: Dois capacitores iguais, submetidos à mesma amplitude de tensão,
porém com frequências diferentes, terão o mesmo valor de “Q”, no entanto, a corrente
através do capacitor é diretamente proporcional à frequência (I = Q/t).
Considerando que a carga máxima do capacitor se dá no valor de pico da tensão
(em qualquer um dos sentidos), mostramos acima as condições para as frequências de
30 e 60Hz ode se observa que a carga máxima é atingida, porém, em tempos
diferentes.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 18
No entanto, levando-se em consideração a expressão: I = Q/t, teremos:
Para 30Hz:
I = Q/t  t = 1/120 = 0,008333s
I = 1/0,00833 = 120 ampères
Para 60Hz:
I = Q/t  t = 1/240 = 0,0041667s
I = 1/0,0041667 = 240 ampères
Logo, comprova-se que a corrente é diretamente proporcional à frequência
Partindo do conceito visto anteriormente, de que a capacitância é a quantidade
de carga armazenada no capacitor podemos concluir que capacitor de maior
capacitância armazena maior carga, conforme indica a expressão:
Q = C.E
A figura acima mostra a relação entre a tensão aplicada e a carga armazenada,
que, sendo as duas tensões de amplitudes e frequências iguais.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 19
Nos circuitos 1 e 2 mostrados na figura, a tensão aplicada é 10 volts e a
frequência 60Hz, porém, as capacitâncias são diferentes.
Nos dois casos o tempo para atingir a carga máxima é o mesmo, porém como as
capacitâncias são diferentes as cargas também serão diferentes.
CIRCUITO 1:
Q = C.E = 0,05F x 10 volts = 0,5C
I = Q/t  t = 0,0041667s
I = 0,5/0,0041667 = 120 ampères
CIRCUITO 2:
Q = C.E = 0,1F x 10 volts = 1C
I = Q/t  t = 0,0041667s
I = 01/0,0041667 = 240 ampères
Logo, comprova-se que a corrente é diretamente proporcional à capacitância
REATÂNCIA CAPACITIVA
Um capacitor oferece oposição à passagem da corrente
forma que uma resistência ou um indutor.
elétrica AC da mesma
Sabemos que a intensidade da corrente AC que um capacitor conduz depende da
frequência, da tensão aplicada e da capacitância.
Evidentemente, a amplitude da tensão aplicada controla o valor da corrente, no
entanto, se a amplitude for mantida constante a corrente dependerá apenas da
capacitância e da frequência.
Num circuito puramente capacitivo, a reatância capacitiva possui o mesmo efeito
que uma resistência num circuito DC ou num circuito AC.
A forma mais conveniente para calcular os efeitos de uma reatância capacitiva
em um circuito AC é usando os princípios da Lei de Ohm.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 20
Xc = reatância capacitiva em ohms
C = capacitância em farads
f = frequência em hertz
Nas curvas acima podemos concluir:
 a variação da reatância capacitiva não é linear com o aumento ou diminuição da
frequência ou capacitância.
 a variação da corrente através do capacitor varia linearmente com o aumento ou
diminuição da frequência ou da capacitância.
As curvas acima mostram uma diminuição da reatância capacitiva e um aumento
linear da corrente.
No caso de aumento da reatância capacitiva ou diminuição da corrente os
gráficos serão invertidos, conforme ilustra a figura a seguir.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 21
A figura a seguir mostra dois circuitos (circuitos 1 e 2) onde muda apenas a
frequência mantendo o valor da amplitude da tensão aplicada e o valor da
capacitância.
A reatância capacitiva (Xc) atua como uma resistência. À medida que a
frequência aumenta, Xc diminui e a corrente no circuito aumenta.
Procedendo aos cálculos:
Circuito 1:
Tensão aplicada: 20 volts
Frequência 10Hz
Xc = 1 / 2πfC
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 22
Xc = 1 / 6,28 x 10 x 100.10-6
Xc = 1 / 0,0063  Xc = 159,236 ohms
I = 20 / 159,236 = 125,6mA
Circuito 2:
Tensão aplicada: 20 volts
Frequência 100Hz
Xc = 1 / 2πfC
Xc = 1 / 6,28 x 100 x 100.10-6
Xc = 1 / 0,0063  Xc = 15,925 ohms
I = 20 / 15,924 = 1,256A
RESISTÊNCIA DE PERDA DO CAPACITOR
Um capacitor tem como principal aplicação em eletrônica o bloqueio de DC e
permitir a passagem da corrente alternada (AC).
Como sabemos, o fluxo da corrente AC num capacitor depende da frequência e
da capacitância, em outras palavras, a resistência para a corrente alternada depende
da reatância capacitiva.
O fluxo de corrente em um capacitor depende então de fatores vistos
anteriormente como:
1.
2.
3.
4.
tipo de dielétrico
área das placas
espessura do dielétrico
quantidade de placas
No entanto, como não existe um isolante perfeito, podemos admitir que entre as
placas dos capacitores , por força do dielétrico, existe uma resistência de perda.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 23
A resistência de perda pode ser comparada a uma resistência em paralelo com
as placas (shunt), que nos capacitores de boa qualidade é da ordem de alguns
megohms.
Logo, quanto mais alta for essa resistência, menor será o efeito sobre o
capacitor, e essa eficiência é denominada fator “Q” do capacitor.
Logo, maior resistência, melhor o fator “Q”.
Embora essas perdas sejam minimizadas quanto melhor for o fator “Q”, justificase o fato de um capacitor após totalmente carregado e removido do circuito, não
manter sua carga indefinidamente.
Além disso, em algumas aplicações devemos levar em consideração também a
resistência de perda das placas e dos fios dos terminais do capacitor, que deve ser
extremamente baixa para capacitores de boa qualidade.
Essa resistência pode ser representada como uma resistência em série,
conforme ilustra a figura.
Eletricidade Básica – Circuitos capacitivos – Capacitores e capacitância
Prof. Edgar Zuim
Página 24