Aula de Física II - Capacitância e Energia

Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Aula de Física II - Capacitância e Energia
Prof.: Leandro Aguiar Fernandes
([email protected])
Universidade do Estado do Rio de Janeiro
Instituto Politécnico - IPRJ/UERJ
Departamento de Engenharia Mecânica e Energia
Graduação em Engenharia Mecânica/Computação
25 de novembro de 2010
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Plano
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Plano
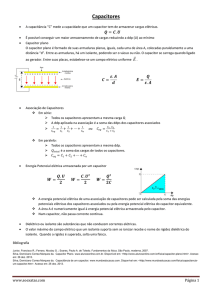
Seja um par de placas metálicas planas paralelas carregadas,
conforme a gura:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Plano
Seja um par de placas metálicas planas paralelas carregadas,
conforme a gura:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Plano
Seja um par de placas metálicas planas paralelas carregadas,
conforme a gura:
O campo elétrico devido às placas (Verique!!!) é dado por:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Plano
Seja um par de placas metálicas planas paralelas carregadas,
conforme a gura:
O campo elétrico devido às placas (Verique!!!) é dado por:
~| =
|E
σ
; σ=
0
Prof.: Leandro Aguiar Fernandes([email protected])
Q
A
Aula de Física II - Capacitância e Energia
(1)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Z
V
≡ V+ − V− =
Prof.: Leandro Aguiar Fernandes([email protected])
−
+
E~ ∗ dl~ = E ∗ d
Aula de Física II - Capacitância e Energia
(2)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Z
V
≡ V+ − V− =
−
+
E~ ∗ dl~ = E ∗ d
(2)
~ aponta no sentido da placa positiva pra negativa.
De fato, pois E
Logo:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Z
V
≡ V+ − V− =
−
+
E~ ∗ dl~ = E ∗ d
(2)
~ aponta no sentido da placa positiva pra negativa.
De fato, pois E
Logo:
V
=
σd
Qd
=
0
0 A
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(3)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Z
V
≡ V+ − V− =
−
+
E~ ∗ dl~ = E ∗ d
(2)
~ aponta no sentido da placa positiva pra negativa.
De fato, pois E
Logo:
V
=
σd
Qd
=
0
0 A
é proporcional à carga Q da placa. Denimos como sendo a
capacitância ζ do par de condutores, que se diz constituir um
capacitor, o coeciente:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(3)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
onde A é a área das placas. A diferença de potencial entre elas é
dada por:
Z
V
≡ V+ − V− =
−
+
E~ ∗ dl~ = E ∗ d
(2)
~ aponta no sentido da placa positiva pra negativa.
De fato, pois E
Logo:
V
=
σd
Qd
=
0
0 A
(3)
é proporcional à carga Q da placa. Denimos como sendo a
capacitância ζ do par de condutores, que se diz constituir um
capacitor, o coeciente:
ζ≡
Q
V
Prof.: Leandro Aguiar Fernandes([email protected])
=
0 A
d
Aula de Física II - Capacitância e Energia
(4)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A unidade de medida de capacitância é o Farad (1F ≡ 11C∨ ). Por
exemplo, para um capacitor de placas planas com 1mm de
distãncia, para ter uma capacitância de 1F, precisaríamos de placas
de área:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A unidade de medida de capacitância é o Farad (1F ≡ 11C∨ ). Por
exemplo, para um capacitor de placas planas com 1mm de
distãncia, para ter uma capacitância de 1F, precisaríamos de placas
de área:
ζ=
0 A
d
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A unidade de medida de capacitância é o Farad (1F ≡ 11C∨ ). Por
exemplo, para um capacitor de placas planas com 1mm de
distãncia, para ter uma capacitância de 1F, precisaríamos de placas
de área:
ζ=
0 A
d
=⇒
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A unidade de medida de capacitância é o Farad (1F ≡ 11C∨ ). Por
exemplo, para um capacitor de placas planas com 1mm de
distãncia, para ter uma capacitância de 1F, precisaríamos de placas
de área:
ζ=
0 A
d
=⇒ A =
dC
0
=
10−3 m ∗ 1F
= 1, 13 ∗ 108 m2
−
12 F
8, 85 ∗ 10 m
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(5)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A unidade de medida de capacitância é o Farad (1F ≡ 11C∨ ). Por
exemplo, para um capacitor de placas planas com 1mm de
distãncia, para ter uma capacitância de 1F, precisaríamos de placas
de área:
ζ=
0 A
d
=⇒ A =
dC
0
=
10−3 m ∗ 1F
= 1, 13 ∗ 108 m2
−
12 F
8, 85 ∗ 10 m
(5)
o que corresponde a 100 km2 , o que mostra que F é uma unidade
de grandes dimensões. As mais usadas são µF e pF .
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Cilíndrico
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Cilíndrico
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Cilíndrico
Neste caso, sendo l o comprimento do capacitor, então:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Cilíndrico
Neste caso, sendo l o comprimento do capacitor, então:
= Ba = 2πQ0 al
0
= − Bb = − 2πQ0 bl
E (a) = σ+
E (b) = − σ−
0
Prof.: Leandro Aguiar Fernandes([email protected])
)
B=
Q
2π0 l
Aula de Física II - Capacitância e Energia
(6)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
≡ V+ − V− =
Z
−
+
E (ρ)d ρ = BV
Prof.: Leandro Aguiar Fernandes([email protected])
Z b
b
dρ
= B ln
ρ
a
a
Aula de Física II - Capacitância e Energia
(7)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
≡ V+ − V− =
Z
−
+
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
o que por (6) dá:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(7)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
≡ V+ − V− =
Z
−
+
E (ρ)d ρ = BV
o que por (6) dá:
ζ=
Prof.: Leandro Aguiar Fernandes([email protected])
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
Aula de Física II - Capacitância e Energia
(7)
(8)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
≡ V+ − V− =
o que por (6) dá:
Z
−
+
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
<< a, então:
ζ=
Se
b = a + d , com d
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(7)
(8)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
Z
≡ V+ − V− =
−
+
o que por (6) dá:
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
<< a, então:
ζ=
Se
b = a + d , com d
b
ln
a
d
= ln 1 +
a
≈
Prof.: Leandro Aguiar Fernandes([email protected])
d
a
Aula de Física II - Capacitância e Energia
(7)
(8)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
Z
≡ V+ − V− =
−
+
o que por (6) dá:
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
<< a, então:
ζ=
Se
b = a + d , com d
b
ln
a
d
= ln 1 +
a
≈
Prof.: Leandro Aguiar Fernandes([email protected])
d
a
=⇒
Aula de Física II - Capacitância e Energia
(7)
(8)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
Z
≡ V+ − V− =
−
+
o que por (6) dá:
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
<< a, então:
(8)
ζ=
Se
b = a + d , com d
b
ln
a
d
= ln 1 +
a
≈
Prof.: Leandro Aguiar Fernandes([email protected])
d
a
=⇒ ζ =
(7)
2π0 al
d
=
0 A
d
Aula de Física II - Capacitância e Energia
(9)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
A diferença de potencial entre os cilindros é:
V
Z
≡ V+ − V− =
−
+
o que por (6) dá:
E (ρ)d ρ = BV
Z b
b
dρ
= B ln
ρ
a
a
2π0 l
ln ba
<< a, então:
(8)
ζ=
Se
b = a + d , com d
b
ln
a
d
= ln 1 +
a
≈
d
a
=⇒ ζ =
(7)
2π0 al
d
=
0 A
d
(9)
onde A = 2π al é a área da superfície lateral do cilindro, ou seja, o
capacitor cilíndrico funciona como um "capacitor plano enrolado".
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Esférico
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Esférico
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Capacitor Esférico
E~ =
Q
4π0 r 2
r̂ ; V
=
Prof.: Leandro Aguiar Fernandes([email protected])
Q
4π0
1
R
1
−
1
R
2
Aula de Física II - Capacitância e Energia
(10)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a capacitância será:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a capacitância será:
ζ = 4π0
Prof.: Leandro Aguiar Fernandes([email protected])
RR
R −R
1
2
2
1
Aula de Física II - Capacitância e Energia
(11)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a capacitância será:
ζ = 4π0
RR
R −R
1
2
2
1
(11)
Caso R2 − R1 = d << R1 , obtemos (9) novamente. Em particular,
se R2 → ∞, obtemos a capacitância de uma esfera de raio R
(ζ = 4π0 R ). As linhas de força vão da superfície da esfera ao
innito. Um exemplo é a Terra, cujo raio é R ≈ 6, 37 ∗ 106 m, o que
dá:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a capacitância será:
ζ = 4π0
RR
R −R
1
2
2
(11)
1
Caso R2 − R1 = d << R1 , obtemos (9) novamente. Em particular,
se R2 → ∞, obtemos a capacitância de uma esfera de raio R
(ζ = 4π0 R ). As linhas de força vão da superfície da esfera ao
innito. Um exemplo é a Terra, cujo raio é R ≈ 6, 37 ∗ 106 m, o que
dá:
F
ζ ≈ 4π ∗ 6, 37 ∗ 106 m ∗ 8, 85 ∗ 10−12 ≈ 710µF
(12)
m
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a capacitância será:
ζ = 4π0
RR
R −R
1
2
2
(11)
1
Caso R2 − R1 = d << R1 , obtemos (9) novamente. Em particular,
se R2 → ∞, obtemos a capacitância de uma esfera de raio R
(ζ = 4π0 R ). As linhas de força vão da superfície da esfera ao
innito. Um exemplo é a Terra, cujo raio é R ≈ 6, 37 ∗ 106 m, o que
dá:
F
ζ ≈ 4π ∗ 6, 37 ∗ 106 m ∗ 8, 85 ∗ 10−12 ≈ 710µF
(12)
m
o que é considerável para que se possa escoar bastante carga para a
Terra sem alterar apreciavelmente seu potencial ("ligação terra").
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Associação de Capacitores
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Associação de Capacitores
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Associação de Capacitores
As placas superiores de uma conexão em paralelo formam um
condutor único, de carga:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Associação de Capacitores
As placas superiores de uma conexão em paralelo formam um
condutor único, de carga:
Q=Q
1
+ Q2 + Q3 = ζ1 V + ζ2 V + ζ3 V = (ζ1 + ζ2 + ζ3 )V = ζeq V
Prof.: Leandro Aguiar Fernandes([email protected])
(13)
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Agora, numa asociação em série de capacitores:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Agora, numa asociação em série de capacitores:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Agora, numa asociação em série de capacitores:
A diferença de potencial entre as extremidades é:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Agora, numa asociação em série de capacitores:
A diferença de potencial entre as extremidades é:
V
=
Q
ζ1
+
Q
ζ2
+
Q
ζ3
=Q
1
ζ1
Prof.: Leandro Aguiar Fernandes([email protected])
+
1
ζ2
+
1
ζ3
=Q
1
ζeq
Aula de Física II - Capacitância e Energia
(14)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
ζ
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
ζ
=⇒
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
ζ
=⇒ U =
Prof.: Leandro Aguiar Fernandes([email protected])
1
ζ
qZ=Q
q dq
q =0
ζ
=
2ζ q
2
0
Aula de Física II - Capacitância e Energia
(15)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
ζ
=⇒ U =
1
ζ
qZ=Q
q dq
q =0
ζ
=
2ζ q
2
0
o que dá:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(15)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
o que dá:
U=
ζ
Q
2
2ζ
=⇒ U =
1
2
1
ζ
= ζV 2 =
Prof.: Leandro Aguiar Fernandes([email protected])
qZ=Q
q dq
q =0
ζ
=
2ζ q
2
(15)
0
1
QV
2
Aula de Física II - Capacitância e Energia
(16)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Energia Eletrostática
Consideremos a carga gradual do capacitor por uma bateria. Num
instante em que a carga armazenada é q, a diferença de potencial
instantânea entre as placas é V = qζ , e a bateria realiza um
trabalho V dq para transferir uma carga adicional dq . Logo:
dU = V dq =
q dq
o que dá:
U=
ζ
Q
2
2ζ
=⇒ U =
1
2
1
ζ
= ζV 2 =
qZ=Q
q dq
q =0
ζ
=
2ζ q
2
1
QV
2
para a energia total armazenada até atingir a carga nal Q.
Prof.: Leandro Aguiar Fernandes([email protected])
(15)
0
Aula de Física II - Capacitância e Energia
(16)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U=
1 0 A 2
V
2 d
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
Prof.: Leandro Aguiar Fernandes([email protected])
V
d
2
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
Prof.: Leandro Aguiar Fernandes([email protected])
V
d
2
=
0 ~ 2
2
E Ad
Aula de Física II - Capacitância e Energia
(17)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
V
d
2
=
0 ~ 2
2
E Ad
(17)
Logo, podemos pensar na energia como estando armazenada no
campo, no espaço entre as placas, como uma densidade de
energia:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
V
d
2
=
0 ~ 2
2
E Ad
(17)
Logo, podemos pensar na energia como estando armazenada no
campo, no espaço entre as placas, como uma densidade de
energia:
u=
U
Ad
Prof.: Leandro Aguiar Fernandes([email protected])
=
0 ~ 2
2
E
Aula de Física II - Capacitância e Energia
(18)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
V
d
2
=
0 ~ 2
2
E Ad
(17)
Logo, podemos pensar na energia como estando armazenada no
campo, no espaço entre as placas, como uma densidade de
energia:
u=
U
Ad
0 ~ 2
E
(18)
2
Consideremos agora uma esfera condutora, isolada, com carga Q.
Tratando-a como um capacitor, a energia potencial armazenada é:
Prof.: Leandro Aguiar Fernandes([email protected])
=
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Para um capacitor plano, isto leva a:
U
1 0 A 2 0
=
V = Ad
2
2 d
V
d
2
=
0 ~ 2
2
E Ad
(17)
Logo, podemos pensar na energia como estando armazenada no
campo, no espaço entre as placas, como uma densidade de
energia:
u=
U
Ad
=
0 ~ 2
=
Q
E
(18)
2
Consideremos agora uma esfera condutora, isolada, com carga Q.
Tratando-a como um capacitor, a energia potencial armazenada é:
U=
Q
2
2ζ
Prof.: Leandro Aguiar Fernandes([email protected])
2
8π0 R
Aula de Física II - Capacitância e Energia
(19)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Prof.: Leandro Aguiar Fernandes([email protected])
Q
4π0 R
Aula de Física II - Capacitância e Energia
(20)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Q
4π0 R
o potencial na superfície, e de ser:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(20)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Q
4π0 R
(20)
o potencial na superfície, e de ser:
1
2
Z
1
2
V σdS = QV
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(21)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Q
4π0 R
(20)
o potencial na superfície, e de ser:
1
2
Z
1
2
V σdS = QV
a energia potencial das cargas distribuídas na superfície com
densidade σ . Supondo (18) válida, então:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(21)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Q
4π0 R
(20)
o potencial na superfície, e de ser:
1
2
Z
1
2
V σdS = QV
a energia potencial das cargas distribuídas na superfície com
densidade σ . Supondo (18) válida, então:
u (~r ) =
0 ~ 2
2
E (~r )
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(21)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
o que também resulta de ser:
V
=
Q
(20)
4π0 R
o potencial na superfície, e de ser:
1
2
Z
1
2
V σdS = QV
(21)
a energia potencial das cargas distribuídas na superfície com
densidade σ . Supondo (18) válida, então:
u (~r ) =
0 ~ 2
2
E (~r ) =
Prof.: Leandro Aguiar Fernandes([email protected])
0
Q
2
2 16π 2 20 r 4
Aula de Física II - Capacitância e Energia
(22)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
dU (r ) = 4πr dr u (r ) =
2
Prof.: Leandro Aguiar Fernandes([email protected])
Q
2
8π0 r 2
dr
Aula de Física II - Capacitância e Energia
(23)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
dU (r ) = 4πr dr u (r ) =
2
Q
2
8π0 r 2
dr
e a energia total contida no campo seria:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(23)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
dU (r ) = 4πr dr u (r ) =
2
Q
2
8π0 r 2
dr
(23)
e a energia total contida no campo seria:
U=
Q
2
8π0
Z∞
R
Prof.: Leandro Aguiar Fernandes([email protected])
dr
Q
=
r
8
π
R
|{z}
2
2
0
= R1
Aula de Física II - Capacitância e Energia
(24)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
dU (r ) = 4πr dr u (r ) =
2
Q
2
8π0 r 2
dr
(23)
e a energia total contida no campo seria:
U=
Q
2
8π0
Z∞
R
dr
Q
=
r
8
π
R
|{z}
2
2
0
= R1
que concorda com (19). De modo geral, podemos armar que:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(24)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Logo, a energia contida numa camada esférica de raio r e espessura
dr seria:
dU (r ) = 4πr dr u (r ) =
2
Q
2
8π0 r 2
dr
(23)
e a energia total contida no campo seria:
U=
Q
2
8π0
Z∞
R
dr
Q
=
r
8
π
R
|{z}
2
2
0
(24)
= R1
que concorda com (19). De modo geral, podemos armar que:
U=
0
2
Z
1
E~ 2 (~r )dV =
Prof.: Leandro Aguiar Fernandes([email protected])
2
Z
ρ(~r )V (~r )dV
Aula de Física II - Capacitância e Energia
(25)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ
~ ∗E
∇
0
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒
~ ∗E
∇
0
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(26)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Então:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(26)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Então:
U=
0
2
~
~ ∗ EdV
(~r )∇
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(26)
(27)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Então:
U=
0
2
~
~ ∗ EdV
(~r )∇
Aplicando a identidade:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(26)
(27)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Então:
U=
0
2
~
~ ∗ EdV
(~r )∇
(26)
(27)
Aplicando a identidade:
~) = V∇
~ + E∇
~ − E2
~ ∗ (V E
~ ∗E
~ V = V∇
~ ∗E
∇
Temos:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(28)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
De fato, se tomarmos a Equação de Poisson:
~ = ρ =⇒ ρ = 0 ∇
~
~ ∗E
~ ∗E
∇
0
Então:
U=
0
2
~
~ ∗ EdV
(~r )∇
(26)
(27)
Aplicando a identidade:
~) = V∇
~ + E∇
~ − E2
~ ∗ (V E
~ ∗E
~ V = V∇
~ ∗E
∇
Temos:
UV
=
0
Z
2 V
E~ dV +
2
Prof.: Leandro Aguiar Fernandes([email protected])
0
Z
2 V
~ )dV
~ ∗ (V E
∇
Aula de Física II - Capacitância e Energia
(28)
(29)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Pelo Teorema da Divergência:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Pelo Teorema da Divergência:
Z
V
~ )dV =
~ ∗ (V E
∇
Prof.: Leandro Aguiar Fernandes([email protected])
I
S
V ~r E~ (~r ) ∗ n̂ dS
Aula de Física II - Capacitância e Energia
(30)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Pelo Teorema da Divergência:
Z
V
~ )dV =
~ ∗ (V E
∇
I
S
V ~r E~ (~r ) ∗ n̂ dS
(30)
Se afastarmos a superfície S indenidamente, V (~r ) sobre S Hcai
~ (~r ) cai como 12 e dS cresce como R 2 . Logo, a
como R1 , E
S cai
R
1
como R e tende a zero para R → ∞. Portanto:
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Pelo Teorema da Divergência:
Z
V
~ )dV =
~ ∗ (V E
∇
I
S
V ~r E~ (~r ) ∗ n̂ dS
(30)
Se afastarmos a superfície S indenidamente, V (~r ) sobre S Hcai
~ (~r ) cai como 12 e dS cresce como R 2 . Logo, a
como R1 , E
S cai
R
1
como R e tende a zero para R → ∞. Portanto:
U=
0
2
Prof.: Leandro Aguiar Fernandes([email protected])
Z
E~ dV
2
Aula de Física II - Capacitância e Energia
(31)
Capacitor Plano
Capacitor Cilíndrico
Capacitor Esférico
Associação de Capacitores
Energia Eletrostática
Pelo Teorema da Divergência:
Z
V
~ )dV =
~ ∗ (V E
∇
I
S
V ~r E~ (~r ) ∗ n̂ dS
(30)
Se afastarmos a superfície S indenidamente, V (~r ) sobre S Hcai
~ (~r ) cai como 12 e dS cresce como R 2 . Logo, a
como R1 , E
S cai
R
1
como R e tende a zero para R → ∞. Portanto:
U=
0
2
Z
E~ dV
2
onde integramos sobre todo o espaço, o que demonstra a (25).
Prof.: Leandro Aguiar Fernandes([email protected])
Aula de Física II - Capacitância e Energia
(31)