Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 8 – CONSERVAÇÃO DE ENERGIA
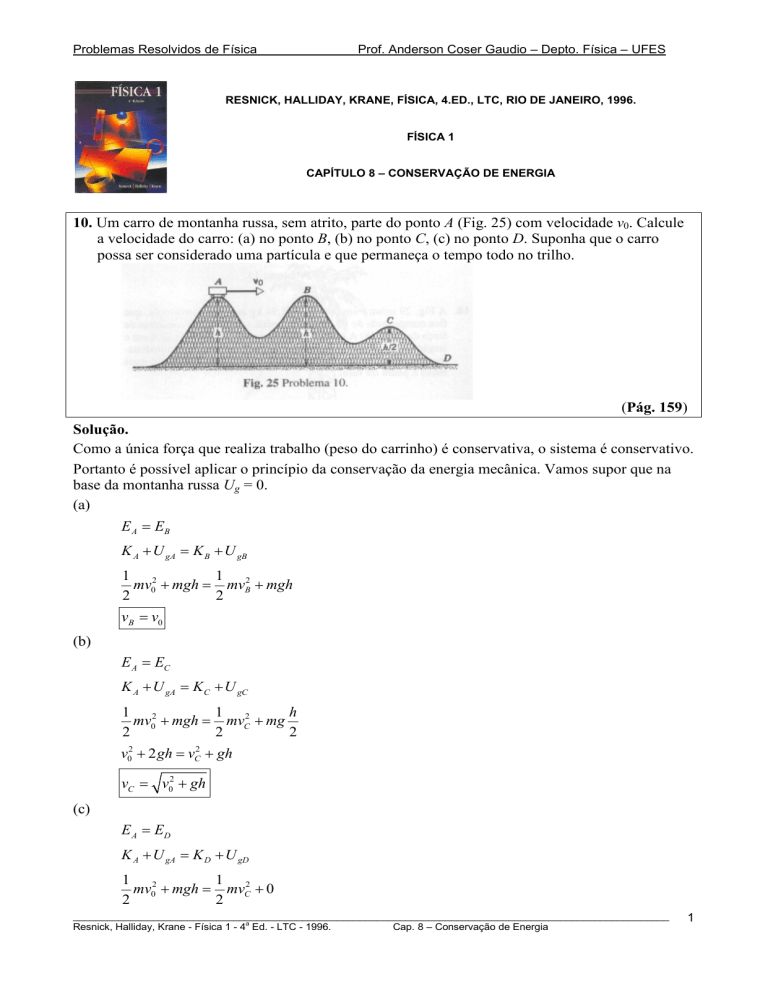
10. Um carro de montanha russa, sem atrito, parte do ponto A (Fig. 25) com velocidade v0. Calcule
a velocidade do carro: (a) no ponto B, (b) no ponto C, (c) no ponto D. Suponha que o carro
possa ser considerado uma partícula e que permaneça o tempo todo no trilho.
(Pág. 159)
Solução.
Como a única força que realiza trabalho (peso do carrinho) é conservativa, o sistema é conservativo.
Portanto é possível aplicar o princípio da conservação da energia mecânica. Vamos supor que na
base da montanha russa Ug = 0.
(a)
E A = EB
K A + U gA =K B + U gB
1 2
1 2
mv0 + mgh =
mvB + mgh
2
2
vB = v0
(b)
E A = EC
K A + U gA = K C + U gC
1 2
1 2
h
mv0 + mgh =
mvC + mg
2
2
2
v02 + 2 gh =vC2 + gh
=
vC
v02 + gh
(c)
E A = ED
K A + U gA = K D + U gD
1 2
1 2
mv0 + mgh =
mvC + 0
2
2
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação de Energia
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
v02 + 2 gh =
vC2
=
vC
v02 + 2 gh
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 1 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação de Energia
2