Capítulo 4

Criptografia e
Segurança de Rede
Capítulo 4
Quarta Edição
por William Stallings
Capítulo 4 – Corpos Finitos
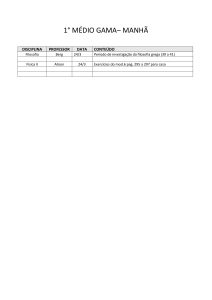
Na manhã seguinte, ao nascer o dia, Star entrou em
casa, aparentemente ávida por uma lição. Eu disse,
"Mostre oito". Ela fez uma exibição brilhante, primeiro
batendo 4-4, depois batendo rapidamente 2-2-2-2,
antes de entrar. É incrível como Star aprendeu a contar
até oito sem dificuldade. E do seu próprio jeito descobriu
que cada número pode ser dado com diferentes
divisões, isso não deixa dúvida de que estava
conscientemente pensando em cada número. De fato,
ela fez a aritmética mental, embora não possa, como os
humanos, dar nome aos números. Mas ela aprendeu a
reconhecer seus nomes falados quase imediatamente e
lembrar dos sons dos nomes. Star é um pássaro
silvestre único que, por vontade própria, buscou a
ciência dos números com ávido interesse e incrível
inteligência.
Living with birds, Len Howard
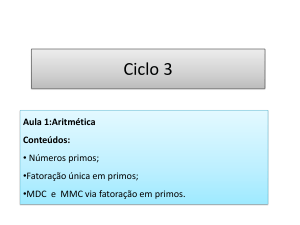
Introdução
 Tópico de importância crescente na criptografia

AES, Curvas Elípticas, IDEA, Chave pública
 Diz respeito à operações com números

Onde o conceito de “número” e os tipos de
operação podem variar consideravelmente.
 Começaremos com conceitos de grupos, anéis
e corpos da álgebra abstrata.
Grupo
 Um conjunto de elementos ou números
 Com algumas operações cujo resultado
também está no conjunto (fechado)
 Obedece:



Associatividade: (a.b).c = a.(b.c)
Possui identidade e: e.a = a.e = a
Possui elemento inverso a-1:a.a-1 = e
 Se for comutativa

a.b = b.a
Então constitui um grupo abeliano.
Grupo Cíclico
 Define-se exponenciação como a
aplicação repetida de um operador

exemplo:
a3 = a.a.a
 A identidade é:
e=a0
 Um grupo é cíclico se cada elemento for
uma potência de um elemento fixo.

Ex.: b = ak para algum a e todo b no grupo
 a é dito gerador do grupo
Anél



Um conjunto de números
Com duas operações (adição e multiplicação)
que formam:
Um grupo comutativo em relação à operação de
adição:





Fechado
Associativo
Distributivo em relação à adição:
• a(b+c) = ab + ac
Se a operação de multiplicação for comutativa,
constitui um anel comutativo
Se a operação de multiplicação tem um
elemento identidade e nenhum divisor que
resulte em zero, consitui um domínio integral
Corpos
 Um conjunto de números
 Com duas operações que formam:



Um grupo comutativo para adição
Um grupo comutativo para multiplicação
(ignorando o 0)
Um anél
 Segue uma hierarquia de axiomas/leis

grupo -> anél -> corpo
Aritmética Modular


Define-se módulo “a
divisão de a por n
Congruência: para a



mod n” como o resto da
= b mod n
Quando divididos por n, a & b tem o mesmo resto
Ex.: 100 mod 11 = 34 mod 11
b é chamado o resíduo de a mod n


Uma vez que com inteiros pode-se sempre escrever:
a = qn + b
Normalmente escolhe-se o menor inteiro positivo
para deixar como resíduo
• 0 <= b <= n-1

o processo é conhecido como Redução de Módulo
Divisores
 Dizemos que b
divide a se a=mb para
algum m, onde a,b e m são inteiros
 b divide a se não houver resto na divisão
 A notação é b|a
 Dizemos que b é um divisor de a
 Ex.: todos 1,2,3,4,6,8,12,24 dividem 24
Operações de Aritmética
Modular
 Usa um número finito de valores e
considera contíguos ambos os extremos
 Aritmética modular considera adição &
multiplicação, com a redução de
módulo do resultado
 Pode-se fazer a redução a qualquer
momento, Ex.:

a+b mod n = [a mod n + b mod n] mod n
Aritmética Modular

Pode-se realizar aritmética modular com
qualquer grupo de inteiros:
– Zn = {0, 1, … , n-1}

Formando um anel comutativo para adição
Com um elemento identidade para multiplicação
Algumas peculiaridades




se (a+b)=(a+c) mod n
então b=c mod n
mas se (a.b)=(a.c) mod n
then b=c mod n somente se a e n forem
primos entre si
Modulo 8 Addition Example
+ 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7 0
2 2 3 4 5 6 7 0 1
3 3 4 5 6 7 0 1 2
4 4 5 6 7 0 1 2 3
5 5 6 7 0 1 2 3 4
6 6 7 0 1 2 3 4 5
7 7 0 1 2 3 4 5 6
Máximo Divisor Comum (MDC)
 Um problema comum na teoria dos
números
 MDC (a,b) de a e b é o maior número que
divide a e b

Ex.: MDC(60,24) = 12
 Dizemos que dois inteiros a e b são
primos entre si quando o MDC = 1


Ex.: MDC(8,15) = 1
8 & 15 são primos entre si
Algoritmo Euclidiano


Um método eficiente para encontrar o MDC(a,b)
Baseado no teorema:


MDC(a,b) = MDC(b, a mod b)
O algoritmo euclidiano para encontrar MDC(a,b)
é:
EUCLID(a,b)
1.
2.
3.
4.
5.
6.
A = a; B = b
if B = 0 return
R = A mod B
A = B
B = R
goto 2
A = mdc(a, b)
Exemplo MDC(1970,1066)
1970 = 1 x 1066 + 904
1066 = 1 x 904 + 162
904 = 5 x 162 + 94
162 = 1 x 94 + 68
94 = 1 x 68 + 26
68 = 2 x 26 + 16
26 = 1 x 16 + 10
16 = 1 x 10 + 6
10 = 1 x 6 + 4
6 = 1 x 4 + 2
4 = 2 x 2 + 0
gcd(1066, 904)
gcd(904, 162)
gcd(162, 94)
gcd(94, 68)
gcd(68, 26)
gcd(26, 16)
gcd(16, 10)
gcd(10, 6)
gcd(6, 4)
gcd(4, 2)
gcd(2, 0)
Corpo de Galois GF(p)
 Pode-se mostrar que o número de
elementos em um corpo finito deve ser a
potência de um número primo p (pn)
 Conhecidos por corpo de Galois
 Denotados por GF(pn)
 De interesse em particular os corpos:
– GF(p)
– GF(2n)
Corpo de Galois GF(p)
 É o conjunto de inteiros {0,1,2...p-1}
juntamente com as operações aritméticas
de módulo p (primo)
 Forma um anel comutativo
GF(7) Exemplo para
Multiplicação
 0 1 2 3 4 5 6
0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6
2 0 2 4 6 1 3 5
3 0 3 6 2 5 1 4
4 0 4 1 5 2 6 3
5 0 5 3 1 6 4 2
6 0 6 5 4 3 2 1
Algoritmo Euclidiano
Extendido
 Encontra não somente o MDC(a,b) = d,
mas também os inteiros x e y que
satisfazem a sequinte relação:
– ax+by = d = MCD(a,b)
Algoritmo Euclidiano
Extendido
EXTENDED EUCLID(m, b)
1. (A1, A2, A3)=(1, 0, m);
(B1, B2, B3)=(0, 1, b)
2. if B3 = 0
return A3 = gcd(m, b); no inverse
3. if B3 = 1
return B3 = gcd(m, b); B2 = b–1 mod m
4. Q = A3 div B3
5. (T1, T2, T3)=(A1 – Q B1, A2 – Q B2, A3 – Q B3)
6. (A1, A2, A3)=(B1, B2, B3)
7. (B1, B2, B3)=(T1, T2, T3)
8. goto 2
Aritmética Polinomial

Um polinômio de grau n é uma expressão na
forma
f(x) = anxn + an-1xn-1 + … + a1x + a0 = ∑ aixi

Podemos distinguir três classes de aritmética de
polinômios:



Aritmética de polinômios ordinária;
Aritmética de polinômios em que a aritmética
sobre os coeficientes é realizada mod p
Aritmética de polinômios em que os coeficientes
estão em GF(p)
Aritmérica Polinomial Comum
 Adição ou subtração dos coeficientes
correspondentes
 Multiplicação de cada termo pelos outros
 Ex.:
let f(x) = x3 + x2 + 2 and g(x) = x2 – x + 1
f(x) + g(x) = x3 + 2x2 – x + 3
f(x) – g(x) = x3 + x + 1
f(x) x g(x) = x5 + 3x2 – 2x + 2
Aritmética de Polinomial com
Coeficientes em Módulo
 No cálculo de do valor de cada
coeficiente, utiliza aritmética de módulo

Forma um anel polinomial
 Pode ser modulo com qualquer número
primo, mas existe interesse especial no
módulo 2.


Isto é, os coeficientes são 0 ou 1
Ex.: f(x) = x3 + x2 e g(x) = x2 + x + 1
f(x) + g(x) = x3 + x + 1
f(x) x g(x) = x5 + x2
Divisão Polinomial
 Pode-se escrever qualquer polinômio da
seguinte forma:



f(x) = q(x) g(x) + r(x)
r(x) é o resto.
r(x) = f(x) mod g(x)
 Se r(x) = 0, diz-se que
g(x) divide f(x)
 se g(x) não tem outro divisor além dele
mesmo & 1 dizemos ser um polinômio
irredutível (ou primo)
 Arimética de módulo com um polinômio
primo constitui um corpo
Encontrando o Máximo
Divisor Comum

Pode-se encontrar o maior divisor comum para
um polinômio


c(x) = MDC(a(x), b(x)) se c(x) for o polinômio de
maior grau que divide os dois a(x), b(x)
Pode-se usar o algoritmo euclidiano pra tal:
EUCLID[a(x), b(x)]
1. A(x) = a(x); B(x) = b(x)
2. if B(x) = 0 return A(x) = mdc[a(x), b(x)]
3. R(x) = A(x) mod B(x)
4. A(x) ¨ B(x)
5. B(x) ¨ R(x)
6. goto 2
Aritmética Polinomial Modular
 Interesse principal em GF(2n)



Polinômios com coeficientes de módulo 2
Cujo grau é inferior a n
Por isso deve-se reduzir o modulo a um
polinômio irredutível de grau n (para
multiplicação somente)
 Isso forma um corpo finito
 Pode-se sempre encontrar o inverso

Usando o algoritmo do Inverso Euclidiano.
Examplo: GF(23)
Considerações
Computacionais
 Como os coeficientes são 0 ou 1, pode-se
representar qualquer polinômio como uma
string de bits
 Adições se tornam um XOR bit a bit
 Multiplicação é deslocamento a esquerda
seguido de um XOR
Exemplo Computacional


para GF(23) temos (x2+1) é 1012 & (x2+x+1) é 1112
Então a adição é:



E a multiplicação é:



(x2+1) + (x2+x+1) = x
101 XOR 111 = 0102
(x+1).(x2+1) = x.(x2+1) + 1.(x2+1)
= x3+x+x2+1 = x3+x2+x+1
011.101 = (101)<<1 XOR (101)<<0 =
1010 XOR 101 = 11112
Redução do modulo polinomial (get q(x) & r(x)) é


(x3+x2+x+1 ) mod (x3+x+1) = 1.(x3+x+1) + (x2) = x2
1111 mod 1011 = 1111 XOR 1011 = 01002
Usando um Gerador
 Técnica equivalente para definir um corpo
finito
 um gerador g é um elemento cujas
potências geram todos os elementos
diferentes de zero
– 0, g0, g1, …, gq-2
 Implementa-se a multiplicação
adicionando expoentes do gerador
Resumo
 Considerações





Conceito de grupos, anéis, corpos
Aritmética modular com inteiros
Algoritmo Euclidiano para MDC
Corpos Finitos GF(p)
Aritmética Polinomial em geral e para GF(2n)