Baixar o arquivo

LISTA DE EXERCÍCIOS - PRA
FENÔMENOS DE TRANSPORTE
A - Viscosidade
1. (Exercício 1.1, pág. 11, Brunetti) A viscosidade cinemática ν de um óleo é
de 0,028 m2/s e o seu peso específico relativo r é de 0,85. Encontrar a
viscosidade dinâmica µ em unidades dos sistemas MKS, CGS e SI. Dado: g =
9,81 m/s2, 1 kgf = 9,81 N, 1 N = 105 dina.
Resp.: μMK*S = 2,43 kgfs/m2; μCGS = 238 dinas/cm2; μSI = 23,8 Ns/m2.
2. (Exercício 1.3, pág. 11, Brunetti) O peso de 3 dm3 de certa substância é 23,5
N. A viscosidade cinemática é 10-5 m2/s. Se g = 9,81 m/s2, qual será a
viscosidade dinâmica μ nos sistemas SI, MK*S e CGS? Dado: 1 d (decímetro) =
10-1 m.
Resp.: μ SI = 7,99 × 10-3 Ns/m2; μ MK*S = 8,14 × 10-4 kgfs/m2; μ CGS = 7,99 × 102
poise.
3. (Exercício 1.4, pág. 12, Brunetti) São dadas duas placas planas paralelas à
distância de 2 mm. A placa superior move-se com velocidade de 4 m/s, enquanto
a inferior é fixa. Se o espaço entre as
placas for preenchido com óleo (ν =
0,1 St; ρ = 830 kg/m3), qual será a
tensão de cisalhamento que agirá no
óleo?
Resp.: τ = 16,6 N/m2.
4. (Exercício 1.5, pág. 12, Brunetti) Uma placa quadrada de 1.0 m de lado e 20
N de peso desliza sobre um plano inclinado de 30°, sobre uma película de óleo.
A velocidade da placa é de 2 m/s constante.
Qual a viscosidade dinâmica do óleo se a
espessura da película é de 2 mm?
Resp.: μ = 10-2 Ns/m2.
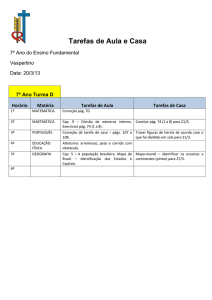
5. (Exercício 1.6, pág. 12, Brunetti) O pistão da figura tem uma massa de 0,5
kg. O cilindro de comprimento ilimitado é
puxado
para
cima
com
velocidade
constante. O diâmetro do cilindro é 10 cm e
do pistão é 9 cm e entre os dois existe óleo
com ν = 10-4 m2/s e γ = 8000 N/m3. Com que
velocidade deve subir o cilindro para que o
pistão permaneça em repouso? Dados: g =
9,81 m/s2; Scircunferência = πD.
Resp.: V = 21,27 m/s.
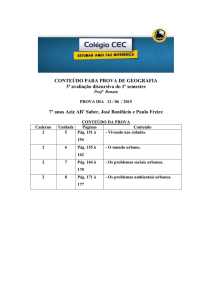
6 . Duas superfícies grandes planas estão separadas por um espaço de 25 mm.
Entre elas encontra-se óleo de massa específica de 850 kg/m 3 e viscosidade
cinemática igual a 7,615x10-5 m2/s. Determinar a força necessária para puxar
uma placa muito fina de 0,4m2 de área a uma velocidade de 0,15 m/s que se
move equidistante entre ambas as superfícies.
7. (Exercício 1.15, pág. 15, Brunetti) A placa da figura tem uma área de 4 m2 e
espessura desprezível. Entre a placa e o solo existe um fluido que escoa,
formando um diagrama de velocidades dado por V = 20y·Vmax·(1 − 5y). A
viscosidade dinâmica do fluido é 10−2 Ns/m2 e a velocidade máxima do
escoamento é 4 m/s. Pede-se: a) o gradiente de velocidades junto ao solo; b) a
força necessária para manter a placa em equilíbrio
. Resp.: a) −80 s−1; b) 3,2 N.
B - Estática dos Fuidos, Manometria
8. (Exercício 2.2, pág. 50, Brunetti) Aplica-se uma força de 200 N na
A na figura. Qual é a força F que deve ser
alavanca AB, como é mostrado
exercida sobre a haste do cilindro para que o sistema permaneça em
equilíbrio? Dado: 𝐴círculo = 𝜋𝑅 2 , 𝑀 = 𝐹𝑑, ∑ 𝑀𝑖 = 0. Resp.: 𝑭 = 10 kN.
B
9. (Exercício 2.5, pág. 50, Brunetti) O manômetro da figura, o fluido A é água
e o fluido B, mercúrio. Qual é a pressão 𝑝1? Dados: 𝛾𝐻𝑔 = 136000 N/m3; 𝛾𝐻2 𝑂
= 10000 N/m3. Resp.: 𝒑𝟏 = 13,35 kPa.
10. A figura abaixo apresenta esquematicamente um manômetro. Pede-se a
diferença de pressões entre os
pontos
A
e
conhecendo-se
B
em
os
Pascal,
seguintes
dados dos pesos específicos e
alturas: 1 = 104 N/m3, 2 = 13,6
 104 N/m3, 3 = 0,8  104 N/m3,
h1 = 1,0 m,
h3 = 2,5 m,
h2 = 2,0 m,
h4 = 5,0 m.
11. No piezômetro inclinado da figura, 𝛾1 = 800 kgf/m3 e 𝛾2 =1700 kgf/m3, 𝐿1 =
20 cm e 𝐿2 = 15 cm e 𝛼 = 30°.
a) Qual a pressão efetiva em Pa no
ponto 𝑃1 ?
b) Qual é a pressão absoluta em mca
no ponto 𝑃1 ?
Dados: 1 atm = 101230 Pa = 10330 kgf/m2
= 10,33 mca. Resp.: a) 𝒑𝐞𝐟𝟏 = 2033,42 Pa, b) 𝒑𝐚𝐛𝐬𝟏 = 10,54 mca.
12. (Exercício 2.6, pág. 51, Brunetti) No manômetro diferencial da figura, o
fluido A é água, B é óleo e o fluido manométrico é mercúrio. Sendo h1 = 25 cm,
h2 = 100 cm, h3 = 80 cm, e h4 = 10 cm, qual é a diferença de pressão pA – pB?
Dados: Dados: 𝛾𝐻𝑔 = 136000 N/m3; 𝛾𝐻2 𝑂 = 10000 N/m3; 𝛾ó𝑙𝑒𝑜 = 8000 N/m3. Resp.:
pA – pB = –132,1 kPa.
13. (Exercício 2.8, pág. 51, Brunetti)
Determinar as pressões efetivas e
absolutas:
a) do ar;
b) no ponto M na configuração a seguir.
Dados: leitura barométrica da pressão atmosférica 740 mmHg; 𝛾ó𝑙𝑒𝑜 = 8500
N/m3; 𝛾𝐻𝑔 = 136000 N/m3; 𝛾𝐻2 𝑂 = 10000 N/m3. Resp: a) pAref = 34 kPa, pArabs =
132,57 kPa; b) pMef = 36,55 kPa, pMabs = 135,12 kPa.
14. Dado o dispositivo da figura, onde h1 = 25 cm, h2 = 10 cm e h3 = 25 cm, h4 =
25 cm, calcular:
a) a pressão do Gás 2;
b) a pressão do Gás 1, sabendo que o manômetro metálico indica uma
pressão de 15000 N/m2;
c) A pressão absoluta do Gás 1, considerando que a pressão atmosférica
local é 730 mmHg.
Dados: γóleo = 8000 N/m3; γHg = 133280 N/m3; γágua = 9800 N/m3. Resp: a) pG2
= 32970 Pa; b) pG1 = 17970 Pa; pABS,G1 = 115204,08 Pa.
C - Empuxo e Peso Aparente
15. (Exemplo 14.5, pág. 69, Halliday & Resnick, V2, 8ª Ed.) Um bloco de
massa específica de B = 800 kg/m3 flutua em um fluido de
massa específica F = 1200 kg/m3. O bloco tem uma altura
H = 6 cm. Qual é a parte h que fica submersa do bloco?
.
Resp.: h = 4 cm.
16. (Exercício 2.45, pág. 63, Brunetti) Um cilindro, de peso específico 𝛾𝑐 =
5000 N/m3, flutua num líquido, conforme mostra a Figura 1. Sob a ação de uma
força 𝐹 = 10000 N, o
cilindro permanece
na posição indicada
na
Figura
2.
Determinar os pesos
específicos
dos
líquidos A e B. Dado: área da base do cilindro = 1 m2. Resp.: 𝜸𝐀 = 15000 N/m3;
𝜸𝐁 = 25000 N/m3.
17. Numa barragem de concreto está instalada uma
comporta circular de ferro fundido com 0,20 m de raio, à
profundidade indicada (figura). Determinar o empuxo que
atua na comporta (utilizar sistema MKS*).
Resp.: F = 528 kgf
18. A figura mostra uma comporta de
largura b = 2 m, instalada no fundo de um
reservatório de água. Algumas dimensões
estão indicadas na figura. Determinar o
módulo do empuxo.
Obs.: Utilize a altura do centro de massa
D - Vazão, Equação de Continuidade
19. (Exercício 3.5, pág. 79, Brunetti) Em um tubo convergente, determinar a
vazão em volume, em massa e a velocidade
média na seção (2), sabendo que o fluido é
água e que A1 = 10 cm2 e A2 = 5 cm2. Dados:
H2O = 1000 kg/m3 e V1 = 1 m/s.
Resp.: 𝒎̇𝟏 = 1 kg/s; Q = 1 l/s; V2 = 2 m/s.
20. (Exercício 3.7, pág. 79, Brunetti) Um tubo admite água (ρ1 = 1000 kg/m3)
num reservatório com uma vazão de 20
L/s. No mesmo reservatório é injetado
óleo (ρ2 = 800 kg/m3) por outro tubo com
uma vazão de 10 L/s. A mistura
homogênea formada é descarregada
por um tubo cuja seção tem uma área de
30 cm2. Determinar a massa específica da mistura no tubo de descarga e a
velocidade da mesma.
Resp.: ρ3 = 933,3 kg/m3; V3 = 10 m/s.
21. (Exercício 3.17, pág. 83, Brunetti) Um
propulsor a jato queima 1 kg/s de combustível
quando o avião voa à velocidade de 200 m/s.
Sabendo que a massa específica do ar = 1,2
kg/m3, a massa específica dos gases
exaustos do propulsor na seção (2) é g = 0,5
kg/m3, a área da seção (1) é A1 = 0,3 m2 e a
área da seção (2) é A2 = 0,2 m2, determine a velocidade dos gases na seção
(2).
Resp.: V2 = 730 m/s.
22. Ar escoa em um tubo divergente, conforme a figura abaixo. A área da menor
seção do tubo é 50 cm2 e a da maior seção é 100
cm2. A velocidade do ar na seção (1) é 18 m/s
enquanto que na seção (2) é 5 m/s. Sendo a
massa específica do ar na seção (1) é 0,026
kg/m3, determine:
a) a massa específica do ar na seção (2);
b) a vazão em massa de ar nas seções (1) e (2);
c) a vazão em volume de ar nas seções (1) e (2).
Dados e informações adicionais: considere regime permanente e lembre-se
que o ar é um fluido compressível e portanto somente a vazão em massa é
conservada. Resp.: a) 2 = 0,0468 kg/m3; b) Qm1 = 0,00234 kg/s e Qm2 =
0,00234 kg/s; c) Q1 = 0,09 m3/s e Q2 = 0,05 m3/s
23. Água a 20 oC escoa em regime permanente através da bifurcação de
tubulação mostrada na figura ao lado,
entrando na seção (1) com vazão volumétrica
de 75 L/min. Os diâmetros nas seções (1) e
(2) são iguais a 2 cm. A velocidade média na
seção (2) é
2,5 m/s. Uma porção do
escoamento é desviada para um chuveiro que contem 100 orifícios de 1 mm de
diâmetro. Considerando uniforme o escoamento na ducha, determine a
velocidade de saída dos jatos do chuveiro.
E - Equação de Bernoulli
24. (Ex. 4.1, pág. 107, Brunetti) Determinar a velocidade do jato do líquido, no
orifício do tanque de grandes dimensões da figura. Considerar fluido ideal.
Resp.: 𝑽 = √𝟐𝒈𝒉.
25. - Quais são as vazões de óleo em massa e em peso no tubo convergente
da figura, para elevar uma coluna de 20 cm de óleo no ponto 0?
Dados:
desprezar as perdas; 𝛾óleo = 8000N/m³; g = 10m/s2. Resp.: a) Qm = 2,1 kg/s; b)
Qp = 21 N/s.
26. - (Ex. 4.4, pág. 107, Brunetti) Um tubo de Pilot é preso num barco que se
desloca a 45 km/h. Qual será a altura 𝒉 alcançada pela água no ramo vertical?
Considere a base do tubo a
uma profundidade 𝑎. Dado:
𝑔 = 9,81 m/s2.
Resp.: 𝒉 = 7,96 m/s.
27 - A água escoa por um tubo cilíndrico e convergente como mostra a figura
ao lado. Determine a vazão em volume de água em L/s sabendo-se que a
diferença de altura no manômetro é constante e igual a 𝐻 = 0,45 m e que o
diâmetro da saída é 𝐷 = 0,05 m. Dados: g = 10 m/s2; 𝛾𝐻2 𝑂 = 10.000 N/m2.
28 . - A água contida em um reservatório elevado, de grandes dimensões,
alimenta por gravidade a linha de engarrafamento, em uma fábrica de água
mineral gasosa, conforme mostra a figura. O reservatório é pressurizado e o
manômetro no topo indica uma pressão de 50 kPa. O diâmetro da tubulação de
descarga é 1,6 cm. Considerando a água um fluido ideal, determine a vazão da
água mineral na saída do tubo. Dado: g = 9,8m/s2.
Resp.: Q2 = 3,46 L/s.