1. (Fuvest 2013) A tabela traz os comprimentos de

LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
1. (Fuvest 2013) A tabela traz os comprimentos de onda no espectro de radiação
eletromagnética, na faixa da luz visível, associados ao espectro de cores mais
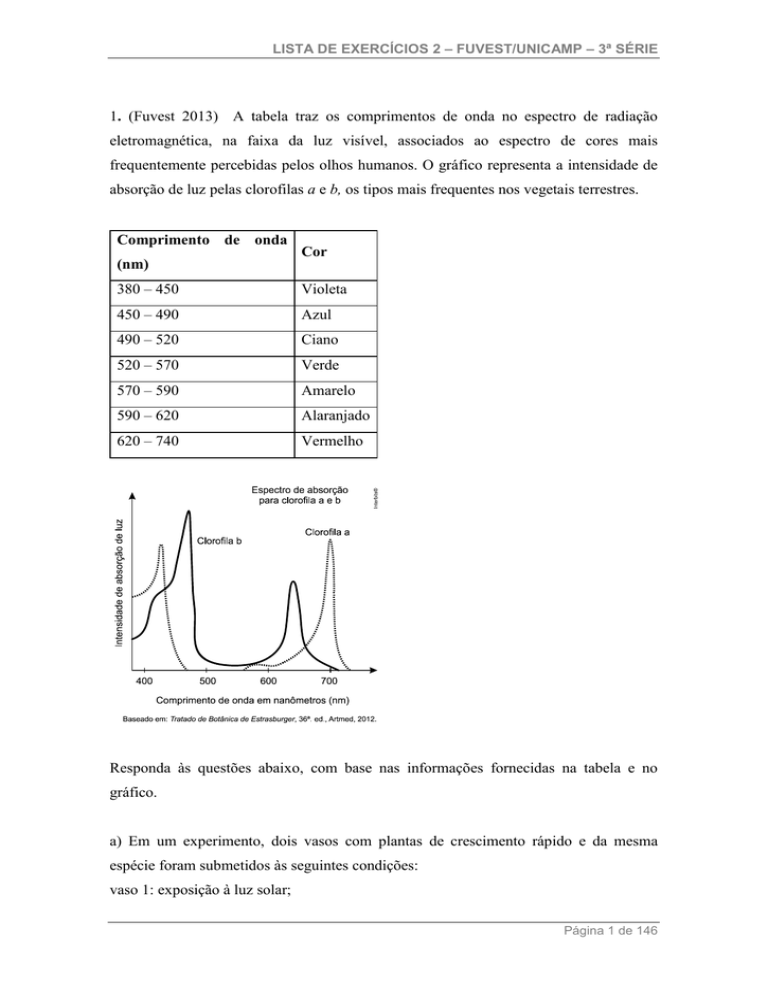
frequentemente percebidas pelos olhos humanos. O gráfico representa a intensidade de
absorção de luz pelas clorofilas a e b, os tipos mais frequentes nos vegetais terrestres.
Comprimento de onda
(nm)
Cor
380 – 450
Violeta
450 – 490
Azul
490 – 520
Ciano
520 – 570
Verde
570 – 590
Amarelo
590 – 620
Alaranjado
620 – 740
Vermelho
Responda às questões abaixo, com base nas informações fornecidas na tabela e no
gráfico.
a) Em um experimento, dois vasos com plantas de crescimento rápido e da mesma
espécie foram submetidos às seguintes condições:
vaso 1: exposição à luz solar;
Página 1 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
vaso 2: exposição à luz verde.
A temperatura e a disponibilidade hídrica foram as mesmas para os dois vasos. Depois
de algumas semanas, verificou-se que o crescimento das plantas diferiu entre os vasos.
Qual a razão dessa diferença?
b) Por que as pessoas, com visão normal para cores, enxergam como verdes, as folhas
da maioria das plantas?
2. (Fuvest 2012) Num ambiente iluminado, ao focalizar um objeto distante, o olho
humano se ajusta a essa situação. Se a pessoa passa, em seguida, para um ambiente de
penumbra, ao focalizar um objeto próximo, a íris
a) aumenta, diminuindo a abertura da pupila, e os músculos ciliares se contraem,
aumentando o poder refrativo do cristalino.
b) diminui, aumentando a abertura da pupila, e os músculos ciliares se contraem,
aumentando o poder refrativo do cristalino.
c) diminui, aumentando a abertura da pupila, e os músculos ciliares se relaxam,
aumentando o poder refrativo do cristalino.
d) aumenta, diminuindo a abertura da pupila, e os músculos ciliares se relaxam,
diminuindo o poder refrativo do cristalino.
e) diminui, aumentando a abertura da pupila, e os músculos ciliares se relaxam,
diminuindo o poder refrativo do cristalino.
3. (Fuvest 2011) As sensações provocadas nos passageiros, dentro de um carrinho,
durante o trajeto em uma montanha-russa, podem ser associadas a determinadas
transformações históricas, como se observa no texto:
A primeira é a da ascensão contínua, metódica e persistente. Essa fase pode
representar o período que vai, mais ou menos, do século XVI até meados do século
XIX. A segunda é a fase em que, num repente, nos precipitamos numa queda
vertiginosa, perdendo as referências do espaço, das circunstâncias que nos cercam e até
o controle das faculdades conscientes. Isso aconteceu por volta de 1870. Nunca é
demais lembrar que esse foi o momento no qual surgiram os parques de diversões e sua
mais espetacular atração, a montanha-russa, é claro. A terceira fase, na nossa imagem da
montanha-russa, é a do “loop”, a síncope final e definitiva, o clímax da aceleração
precipitada. A escala das mudanças desencadeadas, a partir desse momento, é de uma
Página 2 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
tal magnitude que faz os dois momentos anteriores parecerem projeções em câmara
lenta.
N. Sevcenko, No loop da montanha-russa, 2009. Adaptado.
a) Explique duas das fases históricas mencionadas no texto.
b) Na montanha-russa esquematizada abaixo, um motor leva o carrinho até o ponto 1.
Desse ponto, ele parte, saindo do repouso, em direção ao ponto 2, localizado em um
trecho retilíneo, para percorrer o resto do trajeto sob a ação da gravidade (g = 10 m/s2).
Desprezando a resistência do ar e as forças de atrito, calcule
1. o módulo da aceleração tangencial do carrinho no ponto 2.
2. a velocidade escalar do carrinho no ponto 3, dentro do loop.
4. (Unicamp 2015) Movimento browniano é o deslocamento aleatório de partículas
microscópicas suspensas em um fluido, devido às colisões com moléculas do fluido em
agitação térmica.
a) A figura abaixo mostra a trajetória de uma partícula em movimento browniano em
um líquido após várias colisões. Sabendo-se que os pontos negros correspondem a
posições da partícula a cada 30s, qual é o módulo da velocidade média desta partícula
entre as posições A e B?
b) Em um de seus famosos trabalhos, Einstein propôs uma teoria microscópica para
explicar o movimento de partículas sujeitas ao movimento browniano. Segundo essa
teoria, o valor eficaz do deslocamento de uma partícula em uma dimensão é dado por
Página 3 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
I  2 D t, onde t é o tempo em segundos e D  kT r é o coeficiente de difusão de uma
partícula em um determinado fluido, em que k  3 1018 m3 sK, T é a temperatura
absoluta e r é o raio da partícula em suspensão. Qual é o deslocamento eficaz de uma
partícula de raio r  3μm neste fluido a T  300K após 10 minutos?
5. (Unicamp 2012)
O transporte fluvial de cargas é pouco explorado no Brasil,
considerando-se nosso vasto conjunto de rios navegáveis. Uma embarcação navega a
uma velocidade de 26 nós, medida em relação à água do rio (use 1 nó = 0,5 m/s). A
correnteza do rio, por sua vez, tem velocidade aproximadamente constante de 5,0 m/s
em relação às margens. Qual é o tempo aproximado de viagem entre duas cidades
separadas por uma extensão de 40 km de rio, se o barco navega rio acima, ou seja,
contra a correnteza?
a) 2 horas e 13 minutos.
b) 1 hora e 23 minutos.
c) 51 minutos.
d) 37 minutos.
6. (Unicamp 2012) Em 2011 o Atlantis realizou a última missão dos ônibus espaciais,
levando quatro astronautas à Estação Espacial Internacional.
a) A Estação Espacial Internacional gira em torno da Terra numa órbita
aproximadamente circular de raio R = 6800 km e completa 16 voltas por dia. Qual é a
velocidade escalar média da Estação Espacial Internacional?
Página 4 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Próximo da reentrada na atmosfera, na viagem de volta, o ônibus espacial tem
velocidade de cerca de 8000 m/s, e sua massa é de aproximadamente 90 toneladas. Qual
é a sua energia cinética?
7. (Unicamp 2012) Um jogador de futebol chuta uma bola a 30 m do gol adversário. A
bola descreve uma trajetória parabólica, passa por cima da trave e cai a uma distância de
40 m de sua posição original. Se, ao cruzar a linha do gol, a bola estava a 3 m do chão, a
altura máxima por ela alcançada esteve entre
a) 4,1 e 4,4 m.
b) 3,8 e 4,1 m.
c) 3,2 e 3,5 m.
d) 3,5 e 3,8 m.
8. (Fuvest 2012) Nina e José estão sentados em cadeiras, diametralmente opostas, de
uma roda gigante que gira com velocidade angular constante. Num certo momento,
Nina se encontra no ponto mais alto do percurso e José, no mais baixo; após 15 s, antes
de a roda completar uma volta, suas posições estão invertidas. A roda gigante tem raio
R = 20 m e as massas de Nina e José são, respectivamente, MN = 60 kg e MJ = 70 kg.
Calcule
a) o módulo v da velocidade linear das cadeiras da roda gigante;
b) o módulo aR da aceleração radial de Nina e de José;
c) os módulos NN e NJ das forças normais que as cadeiras exercem, respectivamente,
sobre Nina e sobre José no instante em que Nina se encontra no ponto mais alto do
percurso e José, no mais baixo.
Página 5 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
NOTE E ADOTE
π3
Aceleração da gravidade g = 10 m/s2
9. (Fuvest 2012) O gráfico abaixo representa a força F exercida pela musculatura
eretora sobre a coluna vertebral, ao se levantar um peso, em função do ângulo  , entre a
direção da coluna e a horizontal. Ao se levantar pesos com postura incorreta, essa força
pode se tornar muito grande, causando dores lombares e problemas na coluna.
Com base nas informações dadas e no gráfico acima, foram feitas as seguintes
afirmações:
I. Quanto menor o valor de  , maior o peso que se consegue levantar.
II. Para evitar problemas na coluna, um halterofilista deve procurar levantar pesos
adotando postura corporal cujo ângulo  seja grande.
III. Quanto maior o valor de  , menor a tensão na musculatura eretora ao se levantar
um peso.
Está correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
10. (Fuvest 2012)
Página 6 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Um pequeno cata-vento do tipo Savonius, como o esquematizado na figura ao lado,
acoplado a uma bomba d'água, é utilizado em uma propriedade rural. A potência útil P
(W) desse sistema para bombeamento de água pode ser obtida pela expressão
2
P  0,1 A  v3 , em que A (m ) é a área total das pás do cata-vento e v (m/s), a velocidade
do vento. Considerando um cata-vento com área total das pás de 2 m2, velocidade do
vento de 5 m/s e a água sendo elevada de 7,5 m na vertical, calcule
a) a potência útil P do sistema;
b) a energia E necessária para elevar 1 L de água;
c) o volume V1 de água bombeado por segundo;
d) o volume V2 de água, bombeado por segundo, se a velocidade do vento cair pela
metade.
NOTE E ADOTE
Densidade da água = 1 g/cm3.
Aceleração da gravidade g = 10 m/s2.
11. (Fuvest 2012) A energia que um atleta gasta pode ser determinada pelo volume de
oxigênio por ele consumido na respiração. Abaixo está apresentado o gráfico do volume
V de oxigênio, em litros por minuto, consumido por um atleta de massa corporal de 70
kg, em função de sua velocidade, quando ele anda ou corre.
Página 7 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Considerando que para cada litro de oxigênio consumido são gastas 5 kcal e usando as
informações do gráfico, determine, para esse atleta,
a) a velocidade a partir da qual ele passa a gastar menos energia correndo do que
andando;
b) a quantidade de energia por ele gasta durante 12 horas de repouso (parado);
c) a potência dissipada, em watts, quando ele corre a 15 km/h;
d) quantos minutos ele deve andar, a 7 km/h, para gastar a quantidade de energia
armazenada com a ingestão de uma barra de chocolate de 100 g, cujo conteúdo
energético é 560 kcal.
NOTE E ADOTE
1 cal = 4 J.
12. (Unicamp 2012) O óleo lubrificante tem a função de reduzir o atrito entre as partes
em movimento no interior do motor e auxiliar na sua refrigeração. O nível de óleo no
cárter varia com a temperatura do motor, pois a densidade do óleo muda com a
temperatura. A tabela abaixo apresenta a densidade de certo tipo de óleo para várias
temperaturas.
T (ºC)
ρ (kg/litro)
0
0,900
20
0,882
40
0,876
Página 8 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
60
0,864
80
0,852
100
0,840
120
0,829
140
0,817
a) Se forem colocados 4 litros de óleo a 20ºC no motor de um carro, qual será o volume
ocupado pelo óleo quando o motor estiver a 100ºC?
b) A força de atrito que um cilindro de motor exerce sobre o pistão que se desloca em
seu interior tem módulo Fatrito  3,0 N . A cada ciclo o pistão desloca-se 6,0 cm para
frente e 6,0 cm para trás, num movimento de vai e vem. Se a frequência do movimento
do pistão é de 2500 ciclos por minuto, qual é a potência média dissipada pelo atrito?
13. (Unicamp 2012) As eclusas permitem que as embarcações façam a transposição dos
desníveis causados pelas barragens. Além de ser uma monumental obra de engenharia
hidráulica, a eclusa tem um funcionamento simples e econômico. Ela nada mais é do
que um elevador de águas que serve para subir e descer as embarcações. A eclusa de
Barra Bonita, no rio Tietê, tem um desnível de aproximadamente 25 m. Qual é o
aumento da energia potencial gravitacional quando uma embarcação de massa
m  1,2  104 kg é elevada na eclusa?
a) 4,8  102 J
b) 1,2  105 J
c) 3,0  105 J
d) 3,0  106 J
14. (Fuvest 2012) Em uma sala fechada e isolada termicamente, uma geladeira, em
funcionamento, tem, num dado instante, sua porta completamente aberta. Antes da
abertura dessa porta, a temperatura da sala é maior que a do interior da geladeira. Após
a abertura da porta, a temperatura da sala,
a) diminui até que o equilíbrio térmico seja estabelecido.
b) diminui continuamente enquanto a porta permanecer aberta.
c) diminui inicialmente, mas, posteriormente, será maior do que quando a porta foi
aberta.
Página 9 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
d) aumenta inicialmente, mas, posteriormente, será menor do que quando a porta foi
aberta.
e) não se altera, pois se trata de um sistema fechado e termicamente isolado.
15. (Unicamp 2012)
Os balões desempenham papel importante em pesquisas
atmosféricas e sempre encantaram os espectadores. Bartolomeu de Gusmão, nascido em
Santos em 1685, é considerado o inventor do aeróstato, balão empregado como
aeronave. Em temperatura ambiente, Tamb  300 K , a densidade do ar atmosférico vale
ρamb  1,26 kg/m3 . Quando o ar no interior de um balão é aquecido, sua densidade
diminui, sendo que a pressão e o volume permanecem constantes. Com isso, o balão é
acelerado para cima à medida que seu peso fica menor que o empuxo.
a) Um balão tripulado possui volume total V  3,0  106 litros . Encontre o empuxo que
atua no balão.
b) Qual será a temperatura do ar no interior do balão quando sua densidade for reduzida
a ρquente  1,05 kg/m3 ? Considere que o ar se comporta como um gás ideal e note que o
número de moles de ar no interior do balão é proporcional à sua densidade.
16. (Fuvest 2012)
Maria e Luísa, ambas de massa M, patinam no gelo. Luísa vai ao encontro de Maria
com velocidade de módulo V. Maria, parada na pista, segura uma bola de massa m e,
num certo instante, joga a bola para Luísa. A bola tem velocidade de módulo  , na
mesma direção de V . Depois que Luísa agarra a bola, as velocidades de Maria e Luísa,
em relação ao solo, são, respectivamente,
a) 0 ;   V
b)  ;   V / 2
c) m / M ; MV / m
Página 10 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
d) m / M ; (m - MV) / (M  m)
e) (M V / 2 - m)/ M ; (m - MV / 2) / (M  m)
17. (Fuvest 2012) Uma pequena bola de borracha maciça é solta do repouso de uma
altura de 1 m em relação a um piso liso e sólido. A colisão da bola com o piso tem
coeficiente de restituição   0,8 . A altura máxima atingida pela bola, depois da sua
terceira colisão com o piso, é
Note e adote:   V2f /V2i , em que Vf e Vi são, respectivamente, os módulos das
velocidades da bola logo após e imediatamente antes da colisão com o piso.
Aceleração da gravidade g  10 m/s2 .
a) 0,80 m.
b) 0,76 m.
c) 0,64 m.
d) 0,51 m.
e) 0,20 m.
18. (Unicamp 2012) O tempo de viagem de qualquer entrada da Unicamp até a região
central do campus é de apenas alguns minutos. Assim, a economia de tempo obtida,
desrespeitando-se o limite de velocidade, é muito pequena, enquanto o risco de
acidentes aumenta significativamente.
a) Considere que um ônibus de massa M = 9000, viajando a 80 km/h, colide na traseira
de um carro de massa ma  1000 kg que se encontrava parado. A colisão é inelástica, ou
Página 11 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
seja, carro e ônibus seguem grudados após a batida. Calcule a velocidade do conjunto
logo após a colisão.
b) Além do excesso de velocidade, a falta de manutenção do veículo pode causar
acidentes. Por exemplo, o desalinhamento das rodas faz com que o carro sofra a ação de
uma força lateral. Considere um carro com um pneu dianteiro desalinhado de 3°,
conforme a figura acima, gerando uma componente lateral da força de atrito FL em uma
das rodas. Para um carro de massa mb  1600 kg , calcule o módulo da aceleração lateral
do carro, sabendo que o módulo da força de atrito em cada roda vale Fat  8000 N .
Dados: sen 3° = 0,05 e cos 3° = 0,99.
19. (Fuvest 2012) Um móbile pendurado no teto tem três elefantezinhos presos um ao
outro por fios, como mostra a figura. As massas dos elefantes de cima, do meio e de
baixo são, respectivamente, 20g, 30g e 70g. Os valores de tensão, em newtons, nos fios
superior, médio e inferior são, respectivamente, iguais a
Note e adote: Desconsidere as massas dos fios.
Aceleração da gravidade g  10 m/s2 .
a) 1,2; 1,0; 0,7.
b) 1,2; 0,5; 0,2.
c) 0,7; 0,3; 0,2.
d) 0,2; 0,5; 1,2.
e) 0,2; 0,3; 0,7.
20. (Fuvest 2012)
Página 12 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Para ilustrar a dilatação dos corpos, um grupo de estudantes apresenta, em uma feira de
ciências, o instrumento esquematizado na figura acima. Nessa montagem, uma barra de
alumínio com 30cm de comprimento está apoiada sobre dois suportes, tendo uma
extremidade presa ao ponto inferior do ponteiro indicador e a outra encostada num
anteparo fixo. O ponteiro pode girar livremente em torno do ponto O, sendo que o
comprimento de sua parte superior é 10cm e, o da inferior, 2cm. Se a barra de alumínio,
inicialmente à temperatura de 25 ºC, for aquecida a 225 ºC, o deslocamento da
extremidade superior do ponteiro será, aproximadamente, de
Note e adote: Coeficiente de dilatação linear do alumínio: 2  105 ºC1
a) 1 mm.
b) 3 mm.
c) 6 mm.
d) 12 mm.
e) 30 mm.
21. (Unicamp 2012) Em 2015, estima-se que o câncer será responsável por uma dezena
de milhões de mortes em todo o mundo, sendo o tabagismo a principal causa evitável da
doença. Além das inúmeras substâncias tóxicas e cancerígenas contidas no cigarro, a
cada tragada, o fumante aspira fumaça a altas temperaturas, o que leva à morte células
da boca e da garganta, aumentando ainda mais o risco de câncer.
a) Para avaliar o efeito nocivo da fumaça, N0  9,0  104 células humanas foram expostas,
em laboratório, à fumaça de cigarro à temperatura de 72ºC, valor típico para a fumaça
tragada pelos fumantes. Nos primeiros instantes, o número de células que permanecem
vivas em função do tempo t é dado por N(t)  N0 1 

2t 
, onde τ é o tempo necessário
τ 
Página 13 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
para que 90% das células morram. O gráfico abaixo mostra como varia com a
temperatura θ . Quantas células morrem por segundo nos instantes iniciais?
b) A cada tragada, o fumante aspira aproximadamente 35 mililitros de fumaça. A
fumaça possui uma capacidade calorífica molar C  32
J
e um volume molar de 28
K  mol
litros/mol. Assumindo que a fumaça entra no corpo humano a 72ºC e sai a 37ºC, calcule
o calor transferido ao fumante numa tragada
.
22. (Unicamp 2012) A figura abaixo mostra um espelho retrovisor plano na lateral
esquerda de um carro. O espelho está disposto verticalmente e a altura do seu centro
coincide com a altura dos olhos do motorista. Os pontos da figura pertencem a um plano
horizontal que passa pelo centro do espelho. Nesse caso, os pontos que podem ser vistos
pelo motorista são:
a) 1, 4, 5 e 9.
Página 14 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) 4, 7, 8 e 9.
c) 1, 2, 5 e 9.
d) 2, 5, 6 e 9.
23. (Fuvest 2012) Um rapaz com chapéu observa sua imagem em um espelho plano e
vertical. O espelho tem o tamanho mínimo necessário, y = 1,0 m, para que o rapaz, a
uma distância d = 0,5 m, veja a sua imagem do topo do chapéu à ponta dos pés. A
distância de seus olhos ao piso horizontal é h=1,60m. A figura da página de resposta
ilustra essa situação e, em linha tracejada, mostra o percurso do raio de luz relativo à
formação da imagem do ponto mais alto do chapéu.
a) Desenhe, na figura da página de resposta, o percurso do raio de luz relativo à
formação da imagem da ponta dos pés do rapaz.
b) Determine a altura H do topo do chapéu ao chão.
c) Determine a distância Y da base do espelho ao chão.
d) Quais os novos valores do tamanho mínimo do espelho ( y’ ) e da distância da base
do espelho ao chão ( Y’ ) para que o rapaz veja sua imagem do topo do chapéu à ponta
dos pés, quando se afasta para uma distância d’ igual a 1 m do espelho?
NOTE E ADOTE
O topo do chapéu, os olhos e a ponta dos pés do rapaz estão em uma mesma linha
vertical.
24. (Fuvest 2012)
Página 15 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Uma fibra ótica é um guia de luz, flexível e transparente, cilíndrico, feito de sílica ou
polímero, de diâmetro não muito maior que o de um fio de cabelo, usado para transmitir
sinais luminosos a grandes distâncias, com baixas perdas de intensidade. A fibra ótica é
constituída de um núcleo, por onde a luz se propaga e de um revestimento, como
esquematizado na figura acima (corte longitudinal). Sendo o índice de refração do
núcleo 1,60 e o do revestimento, 1,45, o menor valor do ângulo de incidência  do feixe
luminoso, para que toda a luz incidente permaneça no núcleo, é, aproximadamente,
Note e adote
 (graus)
sen 
cos 
25
0,42
0,91
30
0,50
0,87
45
0,71
0,71
50
0,77
0,64
55
0,82
0,57
60
0,87
0,50
65
0,91
0,42
n1 sen 1  n2 sen 2
a) 45º.
b) 50º.
c) 55º.
d) 60º.
e) 65º.
25. (Fuvest 2012)
Página 16 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
O fluxo de íons através de membranas celulares gera impulsos elétricos que regulam
ações fisiológicas em seres vivos. A figura acima ilustra o comportamento do potencial
elétrico V em diferentes pontos no interior de uma célula, na membrana celular e no
líquido extracelular. O gráfico desse potencial sugere que a membrana da célula pode
ser tratada como um capacitor de placas paralelas com distância entre as placas igual à
espessura da membrana, d = 8 nm. No contexto desse modelo, determine
a) o sentido do movimento - de dentro para fora ou de fora para dentro da célula - dos
íons de cloro ( C  ) e de cálcio (Ca2+), presentes nas soluções intra e extracelular;
b) a intensidade E do campo elétrico no interior da membrana;
c) as intensidades FC e FCa das forças elétricas que atuam, respectivamente, nos íons
C

e Ca2+ enquanto atravessam a membrana;
d) o valor da carga elétrica Q na superfície da membrana em contato com o exterior da
célula, se a capacitância C do sistema for igual a 12 pF.
NOTE E ADOTE
Carga do elétron = 1,6  1019 C .
1 pF = 10-12 F.
1 nm = 10-9 m.
C = Q/V.
26. (Unicamp 2012)
Em 1963, Hodgkin e Huxley receberam o prêmio Nobel de
Fisiologia por suas descobertas sobre a geração de potenciais elétricos em neurônios.
Página 17 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Membranas celulares separam o meio intracelular do meio externo à célula, sendo
polarizadas em decorrência do fluxo de íons. O acúmulo de cargas opostas nas
superfícies interna e externa faz com que a membrana possa ser tratada, de forma
aproximada, como um capacitor.
a) Considere uma célula em que íons, de carga unitária e  1,6  1019 C , cruzam a
membrana e dão origem a uma diferença de potencial elétrico de 80mV . Quantos íons
atravessaram a membrana, cuja área é A  5  105 cm2 , se sua capacitância por unidade
de área é Cárea  0,8  106F/cm2 v?
b) Se uma membrana, inicialmente polarizada, é despolarizada por uma corrente de
íons, qual a potência elétrica entregue ao conjunto de íons no momento em que a
diferença de potencial for 20mV e a corrente for 5  108íons/s , sendo a carga de cada íon
e  1,6  1019 C ?
27. (Fuvest 2012)
A figura acima representa, de forma esquemática, a instalação elétrica de uma
residência, com circuitos de tomadas de uso geral e circuito específico para um chuveiro
elétrico. Nessa residência, os seguintes equipamentos permaneceram ligados durante 3
horas a tomadas de uso geral, conforme o esquema da figura: um aquecedor elétrico
(Aq) de 990 W, um ferro de passar roupas de 980 W e duas lâmpadas, L1 e L2, de 60 W
cada uma. Nesse período, além desses equipamentos, um chuveiro elétrico de 4400 W,
Página 18 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
ligado ao circuito específico, como indicado na figura, funcionou durante 12 minutos.
Para essas condições, determine
a) a energia total, em kWh, consumida durante esse período de 3 horas;
b) a corrente elétrica que percorre cada um dos fios fase, no circuito primário do quadro
de distribuição, com todos os equipamentos, inclusive o chuveiro, ligados;
c) a corrente elétrica que percorre o condutor neutro, no circuito primário do quadro de
distribuição, com todos os equipamentos, inclusive o chuveiro, ligados.
NOTE E ADOTE
- A tensão entre fase e neutro é 110 V e, entre as fases, 220 V.
- Ignorar perdas dissipativas nos fios.
- O símbolo  representa o ponto de ligação entre dois fios.
28. (Fuvest 2012) Energia elétrica gerada em Itaipu é transmitida da subestação de Foz
do Iguaçu (Paraná) a Tijuco Preto (São Paulo), em alta tensão de 750 kV, por linhas de
900 km de comprimento. Se a mesma potência fosse transmitida por meio das mesmas
linhas, mas em 30 kV, que é a tensão utilizada em redes urbanas, a perda de energia por
efeito Joule seria, aproximadamente,
a) 27.000 vezes maior.
b) 625 vezes maior.
c) 30 vezes maior.
d) 25 vezes maior.
e) a mesma.
29. (Fuvest 2012) Em uma aula de laboratório, os estudantes foram divididos em dois
grupos. O grupo A fez experimentos com o objetivo de desenhar linhas de campo
elétrico e magnético. Os desenhos feitos estão apresentados nas figuras I, II, III e IV
abaixo.
Página 19 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Aos alunos do grupo B, coube analisar os desenhos produzidos pelo grupo A e formular
hipóteses. Dentre elas, a única correta é que as figuras I, II, III e IV podem representar,
respectivamente, linhas de campo
a) eletrostático, eletrostático, magnético e magnético.
b) magnético, magnético, eletrostático e eletrostático.
c) eletrostático, magnético, eletrostático e magnético.
d) magnético, eletrostático, eletrostático e magnético.
e) eletrostático, magnético, magnético e magnético.
30. (Fuvest 2012)
Página 20 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Um ciclista pedala sua bicicleta, cujas rodas completam uma volta a cada 0,5 segundo.
Em contato com a lateral do pneu dianteiro da bicicleta, está o eixo de um dínamo que
alimenta uma lâmpada, conforme a figura acima. Os raios da roda dianteira da bicicleta
e do eixo do dínamo são, respectivamente, R = 50 cm e r = 0,8 cm. Determine
a) os módulos das velocidades angulares ωR da roda dianteira da bicicleta e ωD do eixo
do dínamo, em rad/s;
b) o tempo T que o eixo do dínamo leva para completar uma volta;
c) a força eletromotriz E que alimenta a lâmpada quando ela está operando em sua
potência máxima.
NOTE E ADOTE
π33
O filamento da lâmpada tem resistência elétrica de 6  quando ela está operando em
sua potência máxima de 24 W.
Considere que o contato do eixo do dínamo com o pneu se dá em R = 50 cm.
31. (Fuvest 2012) A figura abaixo representa imagens instantâneas de duas cordas
flexíveis idênticas, C1 e C2 , tracionadas por forças diferentes, nas quais se propagam
ondas.
Durante uma aula, estudantes afirmaram que as ondas nas cordas C1 e C2 têm:
I. A mesma velocidade de propagação.
II. O mesmo comprimento de onda.
III. A mesma frequência.
Página 21 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Note e adote: A velocidade de propagação de uma onda transversal em uma corda é
igual a
t
, sendo T a tração na corda e  , a densidade linear da corda.

Está correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
32. (Unicamp 2012) Nos últimos anos, o Brasil vem implantando em diversas cidades o
sinal de televisão digital. O sinal de televisão é transmitido através de antenas e cabos,
por ondas eletromagnéticas cuja velocidade no ar é aproximadamente igual à da luz no
vácuo.
a) Um tipo de antena usada na recepção do sinal é a log-periódica, representada na
figura abaixo, na qual o comprimento das hastes metálicas de uma extremidade à outra,
L, é variável. A maior eficiência de recepção é obtida quando L é cerca de meio
comprimento de onda da onda eletromagnética que transmite o sinal no ar (L ~ λ / 2) .
Encontre a menor frequência que a antena ilustrada na figura consegue sintonizar de
forma eficiente, e marque na figura a haste correspondente.
b) Cabos coaxiais são constituídos por dois condutores separados por um isolante de
índice de refração n e constante dielétrica K, relacionados por K  n2 . A velocidade de
uma onda eletromagnética no interior do cabo é dada por v  c / n . Qual é o
comprimento de onda de uma onda de frequência f = 400 MHz que se propaga num
cabo cujo isolante é o polietileno (K=2,25)?
Página 22 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
33. (Unicamp 2012) Raios X, descobertos por Röntgen em 1895, são largamente
utilizados como ferramenta de diagnóstico médico por radiografia e tomografia. Além
disso, o uso de raios X foi essencial em importantes descobertas científicas, como, por
exemplo, na determinação da estrutura do DNA.
a) Em um dos métodos usados para gerar raios X, elétrons colidem com um alvo
metálico perdendo energia cinética e gerando fótons de energia E  hv, sendo
h  6,6  1034 J  s e v a frequência da radiação. A figura abaixo mostra a intensidade da
radiação emitida em função do comprimento de onda, λ . Se toda a energia cinética de
um elétron for convertida na energia de um fóton, obtemos o fóton de maior energia.
Nesse caso, a frequência do fóton torna-se a maior possível, ou seja, acima dela a
intensidade emitida é nula. Marque na figura o comprimento de onda correspondente a
este caso e calcule a energia cinética dos elétrons incidentes
b) O arranjo atômico de certos materiais pode ser representado por planos paralelos
separados por uma distância d. Quando incidem nestes materiais, os raios X sofrem
reflexão especular, como ilustra a figura abaixo. Uma situação em que ocorre
Página 23 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
interferência construtiva é aquela em que a diferença do caminho percorrido por dois
raios paralelos, 2  L, é igual a λ , um comprimento de onda da radiação incidente. Qual
a distância d entre planos para os quais foi observada interferência construtiva em
θ  14,5 usando-se raios X de λ  0,15nm? Dados: sen 14,5  0,25 e cos 14,5  0,97.
34. (Fuvest 2012) Em um laboratório de física, estudantes fazem um experimento em
que radiação eletromagnética de comprimento de onda λ  300 nm incide em uma placa
de sódio, provocando a emissão de elétrons. Os elétrons escapam da placa de sódio com
energia cinética máxima EC  E  W , sendo E a energia de um fóton da radiação e W a
energia mínima necessária para extrair um elétron da placa. A energia de cada fóton é E
= h f, sendo h a constante de Planck e f a frequência da radiação. Determine
a) a frequência f da radiação incidente na placa de sódio;
b) a energia E de um fóton dessa radiação;
c) a energia cinética máxima Ec de um elétron que escapa da placa de sódio;
d) a frequência f0 da radiação eletromagnética, abaixo da qual é impossível haver
emissão de elétrons da placa de sódio.
NOTE E ADOTE
Velocidade da radiação eletromagnética: c  3  108 m/s .
1 nm  109 m.
h  4  1015 eV.s.
W (sódio)  2,3 eV.
1 eV  1,6  1019 J.
TEXTO PARA AS PRÓXIMAS 3 QUESTÕES:
Em setembro de 2010, Júpiter atingiu a menor distância da Terra em muitos anos. As
figuras abaixo ilustram a situação de maior afastamento e a de maior aproximação dos
Página 24 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
planetas, considerando que suas órbitas são circulares, que o raio da órbita terrestre
(RT ) mede 1,5  1011m e que o raio da órbita de Júpiter (RJ ) equivale a 7,5  1011m .
35. (Unicamp 2012) Quando o segmento de reta que liga Júpiter ao Sol faz um ângulo
de 120º com o segmento de reta que liga a Terra ao Sol, a distância entre os dois
planetas é de
a) R2J  RT2  RJRT 3
b) R2J  RT2  RJRT 3
c) R2J  RT2  RJRT
d) R2J  RT2  RJRT
36. (Unicamp 2012) De acordo com a terceira lei de Kepler, o período de revolução e o
2
3
 TJ 
 RJ 
 

 TT 
 RT 
raio da órbita desses planetas em torno do Sol obedecem à relação 
em
que em que TJ e TT são os períodos de Júpiter e da Terra, respectivamente.
Considerando as órbitas circulares representadas na figura, o valor de TJ em anos
terrestres é mais próximo de
Página 25 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
a) 0,1.
b) 5.
c) 12.
d) 125.
37. (Unicamp 2012) A força gravitacional entre dois corpos de massa m1 e m2 tem
módulo F  G
m1m2
r2
, em que r é a distância entre eles e G  6,7  1011
Nm2
kg2
. Sabendo que
a massa de Júpiter é mJ  2,0  1027 kg e que a massa da Terra é mT  6,0  1024 kg , o
módulo da força gravitacional entre Júpiter e a Terra no momento de maior proximidade
é
a) 1,4  1018 N
b) 2,2  1018 N
c) 3,5  1019 N
d) 1,3  1030 N
TEXTO PARA A PRÓXIMA QUESTÃO:
Atualmente há um número cada vez maior de equipamentos elétricos portáteis e isto
tem levado a grandes esforços no desenvolvimento de baterias com maior capacidade de
carga, menor volume, menor peso, maior quantidade de ciclos e menor tempo de
recarga, entre outras qualidades.
38. (Unicamp 2012) Outro exemplo de desenvolvimento, com vistas a recargas rápidas,
é o protótipo de uma bateria de íon-lítio, com estrutura tridimensional. Considere que
uma bateria, inicialmente descarregada, é carregada com uma corrente média im  3,2 A
até atingir sua carga máxima de Q = 0,8 Ah . O tempo gasto para carregar a bateria é de
a) 240 minutos.
b) 90 minutos.
c) 15 minutos.
d) 4 minutos.
Página 26 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
39. (Fuvest 2011) Um automóvel consome, em média, um litro de gasolina para
percorrer, em região urbana, uma distância de 10 km. Esse automóvel é do tipo
conhecido como flex, ou seja, pode utilizar, como combustível, gasolina e/ou álcool,
com as propriedades fornecidas na tabela abaixo. Com base nas informações dadas,
determine:
a) Os valores das energias EG e EA liberadas pela combustão de um litro de gasolina e de
um litro de álcool, respectivamente.
b) A distância dA percorrida, em média, pelo automóvel com 1 litro de álcool.
c) O preço máximo Pm de um litro de álcool, acima do qual não seria conveniente, do
ponto de vista financeiro, utilizar esse combustível, caso o litro de gasolina custasse R$
2,40.
d) O gasto médio G com combustível, por quilômetro rodado pelo automóvel, em região
urbana, usando exclusivamente álcool, se o litro desse combustível custar R$ 1,60.
NOTE E ADOTE
poder
calorífico densidade (g/cm3)
(kcal/kg)
gasolina
1,0 x 104
0,7
álcool
7,0 x 103
0,8
A distância percorrida pelo automóvel é diretamente
proporcional à energia liberada pelo combustível consumido.
40. (Unicamp 2011) Várias Leis da Física são facilmente verificadas em brinquedos
encontrados em parques de diversões. Suponha que em certo parque de diversões uma
criança está brincando em uma roda gigante e outra em um carrossel.
a) A roda gigante de raio R = 20 m gira com velocidade angular constante e executa
uma volta completa em T = 240 s. No gráfico a) abaixo, marque claramente com um
ponto a altura h da criança em relação à base da roda gigante nos instantes t = 60 s, t =
120 s, t = 180 s e t = 240 s, e, em seguida, esboce o comportamento de h em função do
tempo. Considere que, para t = 0, a criança se encontra na base da roda gigante, onde h
= 0.
Página 27 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) No carrossel, a criança se mantém a uma distância r = 4 m do centro do carrossel e
gira com velocidade angular constante 0 . Baseado em sua experiência cotidiana,
estime o valor de 0 para o carrossel e, a partir dele, calcule o módulo da aceleração
centrípeta ac da criança nos instantes t = 10 s, t = 20 s, t = 30 s e t = 40 s. Em seguida,
esboce o comportamento de ac em função do tempo no gráfico b) abaixo, marcando
claramente com um ponto os valores de ac para cada um dos instantes acima. Considere
que, para t = 0, o carrossel já se encontra em movimento.
41. (Fuvest 2011) Os modelos permitem-nos fazer previsões sobre situações reais,
sendo, em geral, simplificações, válidas em certas condições, de questões complexas.
Por exemplo, num jogo de futebol, a trajetória da bola, após o chute, e o débito cardíaco
dos jogadores podem ser descritos por modelos.
Trajetória da bola: quando se despreza a resistência do ar, a trajetória da bola
chutada, sob a ação da gravidade (g = 10 m/s2), é dada por h  d tg  5  d² / v02  (1 + tg2 
), em que v0 é a velocidade escalar inicial (em m/s),  é o ângulo de elevação (em
radianos) e h é a altura (em m) da bola a uma distância d (em m), do local do chute,
conforme figura abaixo.
Página 28 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Débito cardíaco (DC): está relacionado ao volume sistólico VS (volume de
sangue bombeado a cada batimento) e à frequência cardíaca FC pela fórmula DC = VS
x FC.
Utilize esses modelos para responder às seguintes questões:
a) Durante uma partida, um jogador de futebol quer fazer um passe para um
companheiro a 32 m de distância. Seu chute produz uma velocidade inicial na bola de
72 km/h. Calcule os valores de tg  necessários para que o passe caia exatamente nos
pés do companheiro.
b) Dois jogadores, A e B, correndo moderadamente pelo campo, têm frequência
cardíaca de 120 batimentos por minuto. O jogador A tem o volume sistólico igual a 4/5
do volume sistólico do jogador B. Os dois passam a correr mais rapidamente. A
frequência cardíaca do jogador B eleva-se para 150 batimentos por minuto. Para quanto
subirá a frequência cardíaca do jogador A se a variação no débito cardíaco (DCfinal –
DCinicial) de ambos for a mesma?
42. (Fuvest 2011)
Um menino puxa, com uma corda, na direção horizontal, um
cachorro de brinquedo formado por duas partes, A e B, ligadas entre si por uma mola,
como ilustra a figura abaixo. As partes A e B têm, respectivamente, massas mA = 0,5 kg
e mB = 1 kg, sendo  = 0,3 o coeficiente de atrito cinético entre cada parte e o piso. A
constante elástica da mola é k = 10 N/m e, na posição relaxada, seu comprimento é x0 =
10 cm. O conjunto se move com velocidade constante v = 0,1 m/s.
NOTE E ADOTE
Aceleração da gravidade no local: g = 10 m/s2
Página 29 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Despreze a massa da mola.
Nessas condições, determine:
a) O módulo T da força exercida pelo menino sobre a parte B.
b) O trabalho W realizado pela força que o menino faz para puxar o brinquedo por 2
minutos.
c) O módulo F da força exercida pela mola sobre a parte A.
d) O comprimento x da mola, com o brinquedo em movimento.
43. (Fuvest 2011) Usando um sistema formado por uma corda e uma roldana, um
homem levanta uma caixa de massa m, aplicando na corda uma força F que forma um
ângulo  com a direção vertical, como mostra a figura. O trabalho realizado pela
resultante das forças que atuam na caixa
- peso e força da corda -, quando o centro de massa da caixa é elevado, com velocidade
constante v, desde a altura ya até a altura yb, é:
a) nulo.
b) F (yb – ya).
c) mg (yb – ya).
Página 30 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
d) F cos    (yb – ya).
e) mg (yb – ya) + mv2/2.
44. (Unicamp 2011) A importância e a obrigatoriedade do uso do cinto de segurança
nos bancos dianteiros e traseiros dos veículos têm sido bastante divulgadas pelos meios
de comunicação. Há grande negligência especialmente quanto ao uso dos cintos
traseiros. No entanto, existem registros de acidentes em que os sobreviventes foram
apenas os passageiros da frente, que estavam utilizando o cinto de segurança.
a) Considere um carro com velocidade v = 72 km/h que, ao colidir com um obstáculo, é
freado com desaceleração constante até parar completamente após ∆t = 0,1 s. Calcule o
módulo da força que o cinto de segurança exerce sobre um passageiro com massa m =
70 kg durante a colisão para mantê-lo preso no banco até a parada completa do veículo.
b) Um passageiro sem o cinto de segurança pode sofrer um impacto equivalente ao
causado por uma queda de um edifício de vários andares. Considere que, para uma
colisão como a descrita acima, a energia mecânica associada ao impacto vale E = 12 kJ.
Calcule a altura de queda de uma pessoa de massa m = 60 kg, inicialmente em repouso,
que tem essa mesma quantidade de energia em forma de energia cinética no momento
da colisão com o solo.
45. (Fuvest 2011) Um esqueitista treina em uma pista cujo perfil está representado na
figura abaixo. O trecho horizontal AB está a uma altura h = 2,4 m em relação ao trecho,
também horizontal, CD. O esqueitista percorre a pista no sentido de A para D. No
trecho AB, ele está com velocidade constante, de módulo v = 4 m/s; em seguida, desce a
rampa BC, percorre o trecho CD, o mais baixo da pista, e sobe a outra rampa até atingir
uma altura máxima H, em relação a CD. A velocidade do esqueitista no trecho CD e a
altura máxima H são, respectivamente, iguais a
Página 31 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
NOTE E ADOTE
g = 10 m/s2
Desconsiderar:
- Efeitos dissipativos.
- Movimentos do esqueitista em relação ao esqueite.
a) 5 m/s e 2,4 m.
b) 7 m/s e 2,4 m.
c) 7 m/s e 3,2 m.
d) 8 m/s e 2,4 m.
e) 8 m/s e 3,2 m.
46. (Fuvest 2011) Trens de alta velocidade, chamados trens-bala, deverão estar em
funcionamento no Brasil nos próximos anos. Características típicas desses trens são:
velocidade máxima de 300 km/h, massa total (incluindo 500 passageiros) de 500 t e
potência máxima dos motores elétricos igual a 8 MW. Nesses trens, as máquinas
elétricas que atuam como motores também podem ser usadas como geradores, freando o
movimento (freios regenerativos). Nas ferrovias, as curvas têm raio de curvatura de, no
mínimo, 5 km. Considerando um trem e uma ferrovia com essas características,
determine:
a) O tempo necessário para o trem atingir a velocidade de 288 km/h, a partir do repouso,
supondo que os motores forneçam a potência máxima o tempo todo.
b) A força máxima na direção horizontal, entre cada roda e o trilho, numa curva
horizontal percorrida a 288 km/h, supondo que o trem tenha 80 rodas e que as forças
entre cada uma delas e o trilho tenham a mesma intensidade.
c) A aceleração do trem quando, na velocidade de 288 km/h, as máquinas elétricas são
acionadas como geradores de 8 MW de potência, freando o movimento.
NOTE E ADOTE
1 t = 1000 kg
Desconsidere o fato de que, ao partir, os motores demoram alguns segundos para atingir
sua potência máxima.
Página 32 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
47. (Fuvest 2011) Num espetáculo de circo, um homem deita-se no chão do picadeiro e
sobre seu peito é colocada uma tábua, de 30 cm x 30 cm, na qual foram cravados 400
pregos, de mesmo tamanho, que atravessam a tábua. No clímax do espetáculo, um saco
com 20 kg de areia é solto, a partir do repouso, de 5 m de altura em relação à tábua, e
cai sobre ela. Suponha que as pontas de todos os pregos estejam igualmente em contato
com o peito do homem.
Determine:
a) A velocidade do saco de areia ao tocar a tábua de pregos.
b) A força média total aplicada no peito do homem se o saco de areia parar 0,05 s após
seu contato com a tábua.
c) A pressão, em N/cm2, exercida no peito do homem por cada prego, cuja ponta tem 4
mm2 de área.
NOTE E ADOTE
Aceleração da gravidade no local: g = 10 m/s2
Despreze o peso da tábua com os pregos.
Não tente reproduzir esse número de circo!
48. (Fuvest 2011) Um gavião avista, abaixo dele, um melro e, para apanhá-lo, passa a
voar verticalmente, conseguindo agarrá-lo. Imediatamente antes do instante em que o
gavião, de massa MG = 300 g, agarra o melro, de massa MM = 100 g, as velocidades do
gavião e do melro são, respectivamente, VG = 80 km/h na direção vertical, para baixo, e
VM = 24 km/h na direção horizontal, para a direita, como ilustra a figura acima.
Imediatamente após a caça, o vetor velocidade u do gavião, que voa segurando o melro,
forma um ângulo  com o plano horizontal tal que tg  é aproximadamente igual a
Página 33 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
a) 20.
b) 10.
c) 3.
d) 0,3.
e) 0,1.
49. (Fuvest 2011) Para manter-se equilibrado em um tronco de árvore vertical, um picapau agarra-se pelos pés, puxando-se contra o tronco, e apoia sobre ele sua cauda,
constituída de penas muito rígidas, conforme figura ao lado. No esquema abaixo estão
indicadas as direções das forças nos pés (T) e na cauda (C) do pica-pau - que passam
pelo seu centro de massa (CM) – e a distância da extremidade da cauda ao CM do picapau, que tem 1 N de peso (P).
a) Calcule os momentos da forças P e C em relação ao ponto O indicado no esquema.
Página 34 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Escreva a expressão para o momento da força T em relação ao ponto O e determine o
módulo dessa força.
c) Determine o módulo da força C na cauda do pica-pau.
50. (Fuvest 2011) Um forno solar simples foi construído com uma caixa de isopor,
forrada internamente com papel alumínio e fechada com uma tampa de vidro de 40 cm
x 50 cm. Dentro desse forno, foi colocada uma pequena panela contendo 1 xícara de
arroz e 300 ml de água à temperatura ambiente de 25 ºC.
Suponha que os raios solares incidam perpendicularmente à tampa de vidro e que toda a
energia incidente na tampa do forno a atravesse e seja absorvida pela água. Para essas
condições, calcule:
a) A potência solar total P absorvida pela água.
b) A energia E necessária para aquecer o conteúdo da panela até 100 ºC.
c) O tempo total T necessário para aquecer o conteúdo da panela até 100 ºC e evaporar
1/3 da água nessa temperatura (cozer o arroz).
NOTE E ADOTE
Potência solar incidente na superfície da Terra: 1 kW/m2
Densidade da água: 1 g/cm3
Calor específico da água: 4 J/(g ºC)
Calor latente de evaporação da água: 2200 J/g
Desconsidere as capacidades caloríficas do arroz e da panela.
51. (Unicamp 2011) O homem tem criado diversas ferramentas especializadas, sendo
que para a execução de quase todas as suas tarefas há uma ferramenta própria.
a) Uma das tarefas enfrentadas usualmente é a de levantar massas cujo peso excede as
nossas forças. Uma ferramenta usada em alguns desses casos é o guincho girafa,
representado na figura adiante. Um braço móvel é movido por um pistão e gira em torno
do ponto O para levantar uma massa M. Na situação da figura, o braço encontra-se na
v
posição horizontal, sendo D = 2,4 m e d = 0,6 m. Calcule o módulo da força F exercida
pelo pistão para equilibrar uma massa M = 430 kg. Despreze o peso do braço.
Página 35 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Dados: cos 30° = 0,86 e sen 30° = 0,50.
b) Ferramentas de corte são largamente usadas nas mais diferentes situações como, por
exemplo, no preparo dos alimentos, em intervenções cirúrgicas, em trabalhos com
metais e em madeira. Uma dessas ferramentas é o formão, ilustrado na figura adiante,
que é usado para entalhar madeira. A área da extremidade cortante do formão que tem
contato com a madeira é detalhada com linhas diagonais na figura, sobre uma escala
graduada.
Sabendo que o módulo da força exercida por um martelo ao golpear a base do
cabo do formão e F = 4,5 N, calcule a pressão exercida na madeira.
52. (Fuvest 2011) Um objeto decorativo consiste de um bloco de vidro transparente, de
índice de refração igual a 1,4, com a forma de um paralelepípedo, que tem, em seu
interior, uma bolha, aproximadamente esférica, preenchida com um líquido, também
transparente, de índice de refração n. A figura a seguir mostra um perfil do objeto.
Página 36 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Nessas condições, quando a luz visível incide perpendicularmente em uma das faces do
bloco e atravessa a bolha, o objeto se comporta, aproximadamente, como
a) uma lente divergente, somente se n > 1,4.
b) uma lente convergente, somente se n > 1,4.
c) uma lente convergente, para qualquer valor de n.
d) uma lente divergente, para qualquer valor de n.
e) se a bolha não existisse, para qualquer valor de n.
53. (Fuvest 2011) Um jovem pesca em uma lagoa de água transparente, utilizando, para
isto, uma lança. Ao enxergar um peixe, ele atira sua lança na direção em que o observa.
O jovem está fora da água e o peixe está 1 m abaixo da superfície. A lança atinge a água
a uma distância x = 90 cm da direção vertical em que o peixe se encontra, como ilustra a
figura abaixo. Para essas condições, determine:
a) O ângulo  , de incidência na superfície da água, da luz refletida pelo peixe.
b) O ângulo  que a lança faz com a superfície da água.
c) A distância y, da superfície da água, em que o jovem enxerga o peixe.
NOTE E ADOTE
Página 37 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Índice de refração do ar = 1
Índice de refração da água = 1,3
Lei de Snell: v1 / v 2  sen1 / sen2
Ângulo 
sen 
tg 
30º
0,50
0,58
40º
0,64
0,84
42º
0,67
0,90
53º
0,80
1,33
60º
0,87
1,73
54. (Fuvest 2011) O olho é o senhor da astronomia, autor da cosmografia, conselheiro e
corretor de todas as artes humanas (...). É o príncipe das matemáticas; suas disciplinas
são intimamente certas; determinou as altitudes e dimensões das estrelas; descobriu os
elementos e seus níveis; permitiu o anúncio de acontecimentos futuros, graças ao curso
dos astros; engendrou a arquitetura, a perspectiva, a divina pintura (...). O engenho
humano lhe deve a descoberta do fogo, que oferece ao olhar o que as trevas haviam
roubado.
Leonardo da Vinci, Tratado da pintura.
Considere as afirmações abaixo:
I. O excerto de Leonardo da Vinci é um exemplo do humanismo renascentista que
valoriza o racionalismo como instrumento de investigação dos fenômenos naturais e a
aplicação da perspectiva em suas representações pictóricas.
II. Num olho humano com visão perfeita, o cristalino focaliza exatamente sobre a retina
um feixe de luz vindo de um objeto. Quando o cristalino está em sua forma mais
alongada, é possível focalizar o feixe de luz vindo de um objeto distante. Quando o
cristalino encontra-se em sua forma mais arredondada, é possível a focalização de
objetos cada vez mais próximos do olho, até uma distância mínima.
Página 38 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
III. Um dos problemas de visão humana é a miopia. No olho míope, a imagem de um
objeto distante forma-se depois da retina. Para corrigir tal defeito, utiliza-se uma lente
divergente.
Está correto o que se afirma em
a) I, apenas.
b) I e II, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.
55. (Fuvest 2011) O filamento de uma lâmpada incandescente, submetido a uma tensão
U, é percorrido por uma corrente de intensidade i. O gráfico abaixo mostra a relação
entre i e U.
As seguintes afirmações se referem a essa lâmpada.
I. A resistência do filamento é a mesma para qualquer valor da tensão aplicada.
II. A resistência do filamento diminui com o aumento da corrente.
III. A potência dissipada no filamento aumenta com o aumento da tensão aplicada.
Dentre essas afirmações, somente
a) I está correta.
b) II está correta.
c) III está correta.
Página 39 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
d) I e III estão corretas.
e) II e III estão corretas.
56. (Unicamp 2011) O grafeno é um material formado por uma única camada de
átomos de carbono agrupados na forma de hexágonos, como uma colmeia. Ele é um
excelente condutor de eletricidade e de calor e é tão resistente quanto o diamante. Os
pesquisadores Geim e Novoselov receberam o premio Nobel de Física em 2010 por seus
estudos com o grafeno.
a) A quantidade de calor por unidade de tempo  que flui através de um material de
área A e espessura d que separa dois reservatórios com temperaturas distintas T1 e T2, e
dada por  
kA  T2  T1 
, onde k é a condutividade térmica do material. Considere que,
d
em um experimento, uma folha de grafeno de A = 2,8  m2 e d = 1,4 x 10−10 m separa
dois microrreservatórios térmicos mantidos a temperaturas ligeiramente distintas T1 =
300 K e T2 = 302 K. Usando o gráfico abaixo, que mostra a condutividade térmica k do
grafeno em função da temperatura, obtenha o fluxo de calor  que passa pela folha
nessas condições.
b) A resistividade elétrica do grafeno à temperatura ambiente,   1,0  108 m , é menor
que a dos melhores condutores metálicos, como a prata e o cobre. Suponha que dois
eletrodos são ligados por uma folha de grafeno de comprimento L = 1, 4  m e área de
secção transversal A = 70 nm2, e que uma corrente i = 40  A percorra a folha. Qual é a
diferença de potencial entre os eletrodos?
Página 40 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
57. (Fuvest 2011) A conversão de energia solar em energia elétrica pode ser feita com a
utilização de painéis constituídos por células fotovoltaicas que, quando expostas à
radiação solar, geram uma diferença de potencial U entre suas faces. Para caracterizar
uma dessas células (C) de 20 cm2 de área, sobre a qual incide 1 kW/m2 de radiação
solar, foi realizada a medida da diferença de potencial U e da corrente I, variando-se o
valor da resistência R, conforme o circuito esquematizado na figura abaixo.
Os resultados obtidos estão apresentados na tabela.
U (volt)
I (ampère)
0,10
1,0
0,20
1,0
0,30
1,0
0,40
0,98
0,50
0,90
0,52
0,80
0,54
0,75
0,56
0,62
0,58
0,40
0,60
0,00
a) Faça o gráfico da curva I x U na figura a seguir.
Página 41 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Determine o valor da potência máxima Pm que essa célula fornece e o valor da
resistência R nessa condição.
c) Determine a eficiência da célula C para U = 0,3 V.
NOTE E ADOTE
Eficiência 
Pfornecida
Pincidente
58. (Unicamp 2011) Quando dois metais são colocados em contato formando uma
junção, surge entre eles uma diferença de potencial elétrico que depende da temperatura
da junção.
a) Uma aplicação usual desse efeito é a medição de temperatura através da leitura da
diferença de potencial da junção. A vantagem desse tipo de termômetro, conhecido
como termopar, é o seu baixo custo e a ampla faixa de valores de temperatura que ele
pode medir. O gráfico a) abaixo mostra a diferença de potencial U na junção em função
da temperatura para um termopar conhecido como Cromel-Alumel. Considere um balão
fechado que contém um gás ideal cuja temperatura é medida por um termopar CromelAlumel em contato térmico com o balão. Inicialmente o termopar indica que a
temperatura do gás no balão é Ti = 300 K. Se o balão tiver seu volume quadruplicado e
a pressão do gás for reduzida por um fator 3, qual será a variação ∆U = Ufinal − Uinicial da
diferença de potencial na junção do termopar?
b) Outra aplicação importante do mesmo efeito é o refrigerador Peltier. Neste caso, dois
metais são montados como mostra a figura b) abaixo. A corrente que flui pelo anel é
Página 42 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
responsável por transferir o calor de uma junção para a outra. Considere que um Peltier
é usado para refrigerar o circuito abaixo, e que este consegue drenar 10% da potência
total dissipada pelo circuito.
Dados R1 = 0,3  , R2 = 0, 4  e R3 = 1, 2  .
Qual é a corrente ic que circula no circuito, sabendo que o Peltier drena uma
quantidade de calor Q = 540 J em ∆t = 40 s?
59. (Unicamp 2011)
Em 2011 comemoram-se os 100 anos da descoberta da
supercondutividade. Fios supercondutores, que têm resistência elétrica nula, são
empregados na construção de bobinas para obtenção de campos magnéticos intensos.
Esses campos dependem das características da bobina e da corrente que circula por ela.
a) O módulo do campo magnético B no interior de uma bobina pode ser calculado pela
expressão B =  0ni, na qual i e a corrente que circula na bobina, n e o número de
espiras por unidade de comprimento e 0  1,3  106
Tm
. Calcule B no interior de uma
A
Página 43 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
bobina de 25000 espiras, com comprimento L = 0,65 m, pela qual circula uma corrente i
= 80 A.
b) Os supercondutores também apresentam potencial de aplicação em levitação
magnética. Considere um ímã de massa m = 200 g em repouso sobre um material que se
torna supercondutor para temperaturas menores que uma dada temperatura critica TC.
Quando o material é resfriado até uma temperatura T < TC, surge sobre o ímã uma força
v
v
magnética Fm . Suponha que Fm tem a mesma direção e sentido oposto ao da força peso
P do ímã, e que, inicialmente, o ima sobe com aceleração constante de módulo a R = 0,5
m/s2, por uma distância d = 2,0 mm , como ilustrado na figura abaixo. Calcule o
v
trabalho realizado por Fm ao longo do deslocamento do ímã.
60. (Fuvest 2011) Em um ponto fixo do espaço, o campo elétrico de uma radiação
eletromagnética tem sempre a mesma direção e oscila no tempo, como mostra o gráfico
abaixo, que representa sua projeção E nessa direção fixa; E é positivo ou negativo
conforme o sentido do campo.
Página 44 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Radiação
Frequência
eletromagnética
(Hz)
Rádio AM
106
TV (VHF)
108
micro-onda
1010
infravermelha
1012
visível
1014
ultravioleta
1016
raios X
1018
raios 
1020
f
Consultando a tabela acima, que fornece os valores típicos de frequência f para
diferentes regiões do espectro eletromagnético, e analisando o gráfico de E em função
do tempo, é possível classificar essa radiação como
a) infravermelha.
b) visível.
c) ultravioleta.
d) raio X.
e) raio  .
61. (Unicamp 2011) Em 1905 Albert Einstein propôs que a luz é formada por partículas
denominadas fótons. Cada fóton de luz transporta uma quantidade de energia E = h  e
h

possui momento linear p  , em que h  6,6  1034 Js é a constante de Planck e  e 
são, respectivamente, a frequência e o comprimento de onda da luz.
a) A aurora boreal é um fenômeno natural que acontece no Polo Norte, no qual efeitos
luminosos são produzidos por colisões entre partículas carregadas e os átomos dos gases
da alta atmosfera terrestre. De modo geral, o efeito luminoso é dominado pelas
colorações verde e vermelha, por causa das colisões das partículas carregadas com
átomos de oxigênio e nitrogênio, respectivamente.
Página 45 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Calcule a razão R 
Everde
em que Everde é a energia transportada por um fóton
Evermelho
de luz verde com 500 nm,  verde  500 nm, e Evermelho é a energia transportada por um
fóton de luz vermelha com  vermelho  650 nm.
b) Os átomos dos gases da alta atmosfera estão constantemente absorvendo e emitindo
fótons em várias frequências. Um átomo, ao absorver um fóton, sofre uma mudança em
seu momento linear, que é igual, em módulo, direção e sentido, ao momento linear do
fóton absorvido. Calcule o módulo da variação de velocidade de um átomo de massa
m  5,0  1026 kg que absorve um fóton de comprimento de onda  = 660 nm.
62. (Unicamp 2011) A radiação Cerenkov ocorre quando uma partícula carregada
atravessa um meio isolante com uma velocidade maior do que a velocidade da luz nesse
meio. O estudo desse efeito rendeu a Pavel A. Cerenkov e colaboradores o prêmio
Nobel de Física de 1958. Um exemplo desse fenômeno pode ser observado na água
usada para refrigerar reatores nucleares, em que ocorre a emissão de luz azul devido às
partículas de alta energia que atravessam a água.
a) Sabendo-se que o índice de refração da água é n = 1,3, calcule a velocidade máxima
das partículas na água para que não ocorra a radiação Cerenkov. A velocidade da luz no
vácuo é c  3,0  108 m / s .
b) A radiação Cerenkov emitida por uma partícula tem a forma de um cone, como
ilustrado na figura abaixo, pois a sua velocidade, vp , é maior do que a velocidade da luz
no meio, vℓ. Sabendo que o cone formado tem um ângulo  = 50° e que a radiação
emitida percorreu uma distância d = 1,6 m em t = 12 ns, calcule vp .
Dados: cos 50° = 0,64 e sen 50° = 0,76.
Página 46 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
TEXTO PARA A PRÓXIMA QUESTÃO:
O vazamento de petróleo no Golfo do México, em abril de 2010, foi considerado o pior
da história dos EUA. O vazamento causou o aparecimento de uma extensa mancha de
óleo na superfície do oceano, ameaçando a fauna e a flora da região. Estima-se que o
vazamento foi da ordem de 800 milhões de litros de petróleo em cerca de 100 dias.
63. (Unicamp 2011) Quando uma reserva submarina de petróleo é atingida por uma
broca de perfuração, o petróleo tende a escoar para cima na tubulação como
consequência da diferença de pressão, ÄP, entre a reserva e a superfície. Para uma
reserva de petróleo que está a uma profundidade de 2000 m e dado g = 10 m/s2, o menor
valor de ÄP para que o petróleo de densidade ñ = 0,90 g/cm3 forme uma coluna que
alcance a superfície é de
a) 1,8×102 Pa.
b) 1,8×107 Pa.
c) 2,2×105 Pa.
d) 2,2×102 Pa.
TEXTO PARA A PRÓXIMA QUESTÃO:
Acidentes de trânsito causam milhares de mortes todos os anos nas estradas do país.
Pneus desgastados (“carecas”), freios em péssimas condições e excesso de velocidade
são fatores que contribuem para elevar o número de acidentes de trânsito.
Página 47 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
64. (Unicamp 2011)
O sistema de freios ABS (do alemão “Antiblockier-
Bremssystem”) impede o travamento das rodas do veículo, de forma que elas não
deslizem no chão, o que leva a um menor desgaste do pneu. Não havendo deslizamento,
a distância percorrida pelo veículo até a parada completa é reduzida, pois a força de
atrito aplicada pelo chão nas rodas é estática, e seu valor máximo é sempre maior que a
força de atrito cinético. O coeficiente de atrito estático entre os pneus e a pista é ìe =
0,80 e o cinético vale ìc = 0,60. Sendo g = 10 m/s2 e a massa do carro m = 1200 kg, o
módulo da força de atrito estático máxima e a da força de atrito cinético são,
respectivamente, iguais a
a) 1200 N e 12000 N.
b) 12000 N e 120 N.
c) 20000 N e 15000 N.
d) 9600 N e 7200 N.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Em abril de 2010, erupções vulcânicas na Islândia paralisaram aeroportos em vários
países da Europa. Além do risco da falta de visibilidade, as cinzas dos vulcões podem
afetar os motores dos aviões, pois contêm materiais que se fixam nas pás de saída,
causando problemas no funcionamento do motor a jato.
65. (Unicamp 2011) Uma erupção vulcânica pode ser entendida como resultante da
ascensão do magma que contém gases dissolvidos, a pressões e temperaturas elevadas.
Esta mistura apresenta aspectos diferentes ao longo do percurso, podendo ser
esquematicamente representada pela figura a seguir, onde a coloração escura indica o
magma e os discos de coloração clara indicam o gás.
Página 48 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Segundo essa figura, pode-se depreender que
a) as explosões nas erupções vulcânicas se devem, na realidade, à expansão de bolhas de
gás.
b) a expansão dos gases próximos à superfície se deve à diminuição da temperatura do
magma.
c) a ascensão do magma é facilitada pelo aumento da pressão sobre o gás, o que
dificulta a expansão das bolhas.
d) a densidade aparente do magma próximo à cratera do vulcão é maior que nas regiões
mais profundas do vulcão, o que facilita sua subida.
66. (Unicamp 2011) Considere que o calor específico de um material presente nas
cinzas seja c = 0,8 J/g0C . Supondo que esse material entra na turbina a −200C, a energia
cedida a uma massa m = 5g do material para que ele atinja uma temperatura de 8800C é
igual a
a) 220 J.
b) 1000 J.
c) 4600 J.
d) 3600 J.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Quando um rolo de fita adesiva é desenrolado, ocorre uma transferência de cargas
negativas da fita para o rolo, conforme ilustrado na figura a seguir.
Quando o campo elétrico criado pela distribuição de cargas é maior que o campo
elétrico de ruptura do meio, ocorre uma descarga elétrica. Foi demonstrado
Página 49 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
recentemente que essa descarga pode ser utilizada como uma fonte econômica de raiosX.
67. (Unicamp 2011) No ar, a ruptura dielétrica ocorre para campos elétricos a partir de
E = 3,0 x 106 V/m . Suponha que ocorra uma descarga elétrica entre a fita e o rolo para
uma diferença de potencial V = 9 kV. Nessa situação, pode-se afirmar que a distância
máxima entre a fita e o rolo vale
a) 3 mm.
b) 27 mm.
c) 2 mm.
d) 37 nm.
68. (Unicamp 2011) Para um pedaço da fita de área A = 5,0×10−4 m2 mantido a uma
distância constante d = 2,0 mm do rolo, a quantidade de cargas acumuladas é igual a Q
= CV , sendo V a diferença de potencial entre a fita desenrolada e o rolo e C  ε0
que ε0  9,0x1012
A
em
d
C
. Nesse caso, a diferença de potencial entre a fita e o rolo para Q
Vm
= 4,5×10−9C é de
a) 1,2×102 V.
b) 5,0×10−4 V.
c) 2,0×103 V.
d) 1,0×10−20 V.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
O radar é um dos dispositivos mais usados para coibir o excesso de velocidade nas vias
de trânsito. O seu princípio de funcionamento é baseado no efeito Doppler das ondas
eletromagnéticas refletidas pelo carro em movimento.
Considere que a velocidade medida por um radar foi Vm = 72 km/h para um carro que se
aproximava do aparelho.
Página 50 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
69. (Unicamp 2011) Quando um carro não se move diretamente na direção do radar, é
preciso fazer uma correção da velocidade medida pelo aparelho (Vm) para obter a
velocidade real do veículo (Vr). Essa correção pode ser calculada a partir da fórmula Vm
= Vr  cos(á) , em que á é o ângulo formado entre a direção de tráfego da rua e o
segmento de reta que liga o radar ao ponto da via que ele mira. Suponha que o radar
tenha sido instalado a uma distância de 50 m do centro da faixa na qual o carro
trafegava, e tenha detectado a velocidade do carro quando este estava a 130 m de
distância, como mostra a figura a seguir.
Se o radar detectou que o carro trafegava a 72 km/h, sua velocidade real era igual a
a) 66,5 km/h.
b) 78 km/h.
c) 36 3 km/h.
d) 144 / 3 km/h.
70. (Unicamp 2011) Para se obter Vm o radar mede a diferença de frequências Äf, dada
por Äf = f – f0 = ±
Vm
f0, sendo f a frequência da onda refletida pelo carro, f0 = 2,4
c
x1010 Hz a frequência da onda emitida pelo radar e c = 3,0 x108 m/s a velocidade da
onda eletromagnética. O sinal (+ ou -) deve ser escolhido dependendo do sentido do
movimento do carro com relação ao radar, sendo que, quando o carro se aproxima, a
frequência da onda refletida é maior que a emitida.
Pode-se afirmar que a diferença de frequência Äf medida pelo radar foi igual a
a) 1600 Hz.
b) 80 Hz.
Página 51 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
c) –80 Hz.
d) –1600 Hz.
71. (Fuvest 2010) Um avião, com velocidade constante e horizontal, voando em meio a
uma tempestade, repentinamente perde altitude, sendo tragado para baixo e
permanecendo com aceleração constante vertical de módulo a > g, em relação ao solo,
durante um intervalo de tempo ∆t. Pode-se afirmar que, durante esse período, uma bola
de futebol que se encontrava solta sobre uma poltrona desocupada
a) permanecerá sobre a poltrona, sem alteração de sua posição inicial.
b) flutuará no espaço interior do avião, sem aceleração em relação ao mesmo, durante o
intervalo de tempo ∆t.
c) será acelerada para cima, em relação ao avião, sem poder se chocar com o teto,
independentemente do intervalo de tempo ∆t.
d) será acelerada para cima, em relação ao avião, podendo se chocar com o teto,
dependendo do intervalo de tempo ∆t.
e) será pressionada contra a poltrona durante o intervalo de tempo ∆t.
72. (Fuvest 2010) Um consórcio internacional, que reúne dezenas de países, milhares
de cientistas e emprega bilhões de dólares, é responsável pelo Large Hadrons Colider
(LHC), um túnel circular subterrâneo, de alto vácuo, com 27 km de extensão, no qual
eletromagnetos aceleram partículas, como prótons e antiprótons, até que alcancem
11.000 voltas por segundo para, então, colidirem entre si. As experiências realizadas no
LHC investigam componentes elementares da matéria e reproduzem condições de
energia que teriam existido por ocasião do Big Bang.
a) Calcule a velocidade do próton, em km/s, relativamente ao solo, no instante da
colisão.
b) Calcule o percentual dessa velocidade em relação à velocidade da luz, considerada,
para esse cálculo, igual a 300.000 km/s.
c) Além do desenvolvimento científico, cite outros dois interesses que as nações
envolvidas nesse consórcio teriam nas experiências realizadas no LHC.
73. (Fuvest 2010) Astrônomos observaram que a nossa galáxia, a Via Láctea, está a
2,5×106 anos-luz de Andrômeda, a galáxia mais próxima da nossa.
Página 52 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Com base nessa informação, estudantes em uma sala de aula afirmaram o seguinte:
I. A distância entre a Via Láctea e Andrômeda é de 2,5 milhões de km.
II. A distância entre a Via Láctea e Andrômeda é maior que 2×1019 km.
III. A luz proveniente de Andrômeda leva 2,5 milhões de anos para chegar à Via
Láctea.
Está correto apenas o que se afirma em
Dado: 1 ano tem aproximadamente 3×107 s.
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
74. (Fuvest 2010) Uma pessoa (A) pratica corrida numa pista de 300 m, no sentido
anti-horário, e percebe a presença de outro corredor (B) que percorre a mesma pista no
sentido oposto. Um desenho esquemático da pista é mostrado a seguir, indicando a
posição AB do primeiro encontro entre os atletas. Após 1 min e 20 s, acontece o
terceiro encontro entre os corredores, em outra posição, localizada a 20 m de AB, e
indicada na figura por A’B’ (o segundo encontro ocorreu no lado oposto da pista).
Sendo VA e VB os módulos das velocidades dos atletas A e B, respectiva mente, e
sabendo que ambas são constantes, determine
a) VA e VB.
b) a distância percorrida por A entre o primeiro e o segundo encontros, medida ao longo
da pista.
Página 53 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
c) quantas voltas o atleta A dá no intervalo de tempo em que B completa 8 voltas na
pista.
Dados:
1 volta: L = 300 m; tempo para o terceiro encontro: t3 = 1 min e 20 s = 80 s.
75. (Fuvest 2010) Pedro atravessa a nado, com velocidade constante, um rio de 60 m de
largura e margens paralelas, em 2 minutos.
Ana, que boia no rio e está parada em relação à água, observa Pedro, nadando no
sentido sul-norte, em uma trajetória retilínea, perpendicular às margens. Marta, sentada
na margem do rio, vê que Pedro se move no sentido sudoeste-nordeste, em uma
trajetória que forma um ângulo č com a linha perpendicular às margens. As trajetórias,
como observadas por Ana e por Marta, estão indicadas nas figuras a seguir,
respectivamente por PA e PM.
Se o ângulo č for tal que cos č =
4
3 
sen   , qual o valor do módulo da velocidade
5 
5
a) de Pedro em relação à água?
b) de Pedro em relação à margem?
c) da água em relação à margem?
76. (Unicamp 2010) A Copa do Mundo é o segundo maior evento desportivo do
mundo, ficando atrás apenas dos Jogos Olímpicos. Uma das regras do futebol que gera
polêmica com certa frequência é a do impedimento. Para que o atacante A não esteja em
Página 54 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
impedimento, deve haver ao menos dois jogadores adversários a sua frente, G e Z, no
exato instante em que o jogador L lança a bola para A (ver figura). Considere que
somente os jogadores G e Z estejam à frente de A e que somente A e Z se deslocam nas
situações descritas a seguir.
a) Suponha que a distância entre A e Z seja de 12 m. Se A parte do repouso em direção
ao gol com aceleração de 3,0 m/s2 e Z também parte do repouso com a mesma
aceleração no sentido oposto, quanto tempo o jogador L tem para lançar a bola depois
da partida de A antes que A encontre Z?
b) O árbitro demora 0,1 s entre o momento em que vê o lançamento de L e o momento
em que determina as posições dos jogadores A e Z. Considere agora que A e Z movemse a velocidades constantes de 6,0 m/s, como indica a figura. Qual é a distância mínima
entre A e Z no momento do lançamento para que o árbitro decida de forma inequívoca
que A não está impedido?
77. (Fuvest 2010) Na Cidade Universitária (USP), um jovem, em um carrinho de
rolimã, desce a rua do Matão, cujo perfil está representado na figura a seguir, em um
sistema de coordenadas em que o eixo Ox tem a direção horizontal.
No instante t = 0, o carrinho passa em movimento pela posição y = y0 e x = 0.
Página 55 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Dentre os gráficos das figuras a seguir, os que melhor poderiam descrever a posição x e
a velocidade v do carrinho em função do tempo t são, respectivamente,
a) I e II.
b) I e III.
c) II e IV.
d) III e II.
e) IV e III.
78. (Fuvest 2010) Numa filmagem, no exato instante em que um caminhão passa por
uma marca no chão, um dublê se larga de um viaduto para cair dentro de sua caçamba.
A velocidade v do caminhão é constante e o dublê inicia sua queda a partir do repouso,
de uma altura de 5 m da caçamba, que tem 6 m de comprimento. A velocidade ideal do
caminhão é aquela em que o dublê cai bem no centro da caçamba, mas a velocidade real
v do caminhão poderá ser diferente e ele cairá mais à frente ou mais atrás do centro da
caçamba. Para que o dublê caia dentro da caçamba, v pode diferir da velocidade ideal,
em módulo, no máximo:
a) 1 m/s.
b) 3 m/s.
c) 5 m/s.
d) 7 m/s.
e) 9 m/s.
Página 56 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
79. (Unicamp 2010) Quando uma pessoa idosa passa a conviver com seus filhos e
netos, o convívio de diferentes gerações no mesmo ambiente altera a rotina diária da
família de diversas maneiras.
a) O acesso do idoso a todos os locais da casa deve ser facilitado para diminuir o risco
de uma queda ou fratura durante sua locomoção. Pesquisas recentes sugerem que uma
estrutura óssea periférica de um indivíduo jovem suporta uma pressão máxima P1 =
1,2×109 N/m2, enquanto a de um indivíduo idoso suporta uma pressão máxima P2 =
2,0×108 N/m2. Considere que em um indivíduo jovem essa estrutura óssea suporta uma
força máxima F1 = 24 N aplicada sob uma área A1 e que essa área sob a ação da força
diminui com a idade, de forma que A2 = 0,8A1 para o indivíduo idoso. Calcule a força
máxima que a estrutura óssea periférica do indivíduo idoso pode suportar.
b) Na brincadeira “Serra, serra, serrador. Serra o papo do vovô. Serra, serra, serrador.
Quantas tábuas já serrou?”, o avô realiza certo número de oscilações com seu neto
conforme representado na figura a seguir. Em uma oscilação completa (A-O-A) a cabeça
do menino se desloca em uma trajetória circular do ponto A para o ponto O e de volta
para o ponto A. Considerando um caso em que o tempo total de duração da brincadeira é
t = 10 s e a velocidade escalar média da cabeça do menino em cada oscilação (A-O-A)
vale v = 0,6 m/s, obtenha o número total de oscilações (A-O-A) que o avô realizou com
o neto durante a brincadeira. Use h = 50 cm e đ = 3.
80. (Fuvest 2010) Uma pessoa pendurou um fio de prumo no interior de um vagão de
trem e percebeu, quando o trem partiu do repouso, que o fio se inclinou em relação à
vertical. Com auxílio de um transferidor, a pessoa determinou que o ângulo máximo de
inclinação, na partida do trem, foi 14°.
Página 57 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Nessas condições,
a) represente, na figura da página de resposta, as forças que agem na massa presa ao fio.
b) indique, na figura da página de resposta, o sentido de movimento do trem.
c) determine a aceleração máxima do trem.
NOTE E ADOTE:
tg 14° = 0,25.
aceleração da gravidade na Terra, g = 10 m/s2.
81. (Unicamp 2010) Em determinados meses do ano observa-se significativo aumento
do número de estrelas cadentes em certas regiões do céu, número que chega a ser da
ordem de uma centena de estrelas cadentes por hora. Esse fenômeno é chamado de
chuva de meteoros ou chuva de estrelas cadentes, e as mais importantes são as chuvas
de Perseidas e de Leônidas. Isso ocorre quando a Terra cruza a órbita de algum cometa
que deixou uma nuvem de partículas no seu caminho. Na sua maioria, essas partículas
são pequenas como grãos de poeira, e, ao penetrarem na atmosfera da Terra, são
aquecidas pelo atrito com o ar e produzem os rastros de luz observados.
a) Uma partícula entra na atmosfera terrestre e é completamente freada pela força de
atrito com o ar após se deslocar por uma distância de 1,5 km. Se sua energia cinética
inicial é igual a Ec = 4,5 ×104J , qual é o módulo da força de atrito média? Despreze o
trabalho do peso nesse deslocamento.
b) Considere que uma partícula de massa m = 0,1 g sofre um aumento de temperatura de
Äè = 2400 0C após entrar na atmosfera. Calcule a quantidade de calor necessária para
produzir essa elevação de temperatura se o calor específico do material que compõe a
partícula é c = 0,90
J
.
g.C
Página 58 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
82. (Unicamp 2010) Em 1948 Casimir propôs que, quando duas placas metálicas, no
vácuo, são colocadas muito próximas, surge uma força atrativa entre elas, de natureza
eletromagnética, mesmo que as placas estejam descarregadas. Essa força é muitas vezes
relevante no desenvolvimento de mecanismos nanométricos.
a) A força de Casimir é inversamente proporcional à quarta potência da distância entre
as placas. Essa força pode ser medida utilizando-se microscopia de força atômica
através da deflexão de uma alavanca, como mostra a figura a seguir. A força de
deflexão da alavanca se comporta como a força elástica de uma mola. No experimento
ilustrado na figura, o equilíbrio entre a força elástica e a força atrativa de Casimir ocorre
quando a alavanca sofre uma deflexão de Äx = 6,4 nm. Determine a constante elástica
da alavanca, sabendo que neste caso o módulo da força de Casimir é dado por Fc 
b
,
d4
em que b = 9,6×10−39 N.m4 e d é a distância entre as placas. Despreze o peso da placa.
b) Um dos limites da medida da deflexão da alavanca decorre de sua vibração natural
em razão da energia térmica fornecida pelo ambiente. Essa energia é dada por ET = kBT ,
em que kB 1, 4x10–23 J/K e T é a temperatura do ambiente na escala Kelvin.
Considerando que toda a energia ET é convertida em energia elástica, determine a
deflexão Äx produzida na alavanca a T = 300 K se a constante elástica vale kB = 0, 21
N/m.
83. (Unicamp 2010) Em 2009 foram comemorados os 40 anos da primeira missão
tripulada à Lua, a Missão Apollo 11, comandada pelo astronauta norte-americano Neil
Armstrong. Além de ser considerado um dos feitos mais importantes da história recente,
esta viagem trouxe grande desenvolvimento tecnológico.
Página 59 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
a) A Lua tem uma face oculta, erroneamente chamada de lado escuro, que nunca é vista
da Terra. O período de rotação da Lua em torno de seu eixo é de cerca de 27 dias.
Considere que a órbita da Lua em torno da Terra é circular, com raio igual a r = 3,8 ×
108m. Lembrando que a Lua sempre apresenta a mesma face para um observador na
Terra, calcule a sua velocidade orbital em torno da Terra.
b) Um dos grandes problemas para enviar um foguete à Lua é a quantidade de energia
cinética necessária para transpor o campo gravitacional da Terra, sendo que essa energia
depende da massa total do foguete. Por este motivo, somente é enviado no foguete o que
é realmente essencial. Calcule qual é a energia necessária para enviar um tripulante de
massa m = 70 kg à Lua. Considere que a velocidade da massa no lançamento deve ser v
= 2gRT para que ela chegue até a Lua, sendo g a aceleração da gravidade na superfície
na Terra e RT = 6,4  106 m o raio da Terra.
84. (Fuvest 2010) A partícula neutra conhecida como méson K0 é instável e decai,
emitindo duas partículas, com massas iguais, uma positiva e outra negativa, chamadas,
respectivamente, méson π  e méson π  . Em um experimento, foi observado o
decaimento de um K0, em repouso, com emissão do par π  e π  . Das figuras a seguir,
qual poderia representar as direções e sentidos das velocidades das partículas π  e π 
no sistema de referência em que o K0 estava em repouso?
a)
b)
c)
d)
Página 60 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
e)
85. (Unicamp 2010) O lixo espacial é composto por partes de naves espaciais e satélites
fora de operação abandonados em órbita ao redor da Terra. Esses objetos podem colidir
com satélites, além de pôr em risco astronautas em atividades extraveiculares.
Considere que durante um reparo na estação espacial, um astronauta substitui um painel
solar, de massa mp = 80 kg, cuja estrutura foi danificada. O astronauta estava
inicialmente em repouso em relação à estação e ao abandonar o painel no espaço, lançao com uma velocidade vp = 0,15 m/s.
a) Sabendo que a massa do astronauta é ma = 60 kg, calcule sua velocidade de recuo.
b) O gráfico a seguir mostra, de forma simplificada, o módulo da força aplicada pelo
astronauta sobre o painel em função do tempo durante o lançamento. Sabendo que a
variação de momento linear é igual ao impulso, cujo módulo pode ser obtido pela área
do gráfico, calcule a força máxima Fmax.
86. (Unicamp 2010) A Lua não tem atmosfera, diferentemente de corpos celestes de
maior massa. Na Terra, as condições propícias para a vida ocorrem na troposfera, a
camada atmosférica mais quente e densa que se estende da superfície até cerca de 12 km
de altitude.
a) A pressão atmosférica na superfície terrestre é o resultado do peso exercido pela
coluna de ar atmosférico por unidade de área, e ao nível do mar ela vale P0 = 100 kPa.
Na cidade de Campinas, que está a 700 m acima do nível do mar, a pressão atmosférica
Página 61 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
vale P1 = 94 kPa. Encontre a densidade do ar entre o nível do mar e a altitude de
Campinas, considerando-a uniforme entre essas altitudes.
b) Numa viagem intercontinental um avião a jato atinge uma altitude de cruzeiro de
cerca de 10 km. Os gráficos a seguir mostram as curvas da pressão (P) e da temperatura
(T) médias do ar atmosférico em função da altitude para as camadas inferiores da
atmosfera. Usando os valores de pressão e temperatura desses gráficos e considerando
que o ar atmosférico se comporta como um gás ideal, encontre o volume de um mol de
ar a 10 km de altitude. A constante universal dos gases é R = 8,3
J
.
mol K
87. (Fuvest 2010) Um balão de ar quente é constituído de um envelope (parte inflável),
cesta para três passageiros, queimador e tanque de gás. A massa total do balão, com três
passageiros e com o envelope vazio, é de 400 kg. O envelope totalmente inflado tem um
volume de 1500 m3.
a) Que massa de ar M1 caberia no interior do envelope, se totalmente inflado, com
pressão igual a pressão atmosférica local (Patm) e temperatura T = 27 °C?
b) Qual a massa total de ar M2, no interior do envelope, após este ser totalmente inflado
com ar quente a uma temperatura de 127 °C e pressão Patm?
c) Qual a aceleração do balão, com os passageiros, ao ser lançado nas condições dadas
no item b) quando a temperatura externa é T = 27 °C ?
NOTE E ADOTE:
Densidade do ar a 27°C e à pressão atmosférica local = 1,2 kg/m3.
Aceleração da gravidade na Terra, g = 10 m/s2.
Página 62 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Considere todas as operações realizadas ao nível do mar.
Despreze o empuxo acarretado pelas partes sólidas do balão.
T (K) = T (°C) + 273
88. (Fuvest 2010) Energia térmica, obtida a partir da conversão de energia solar, pode
ser armazenada em grandes recipientes isolados, contendo sais fundidos em altas
temperaturas. Para isso, pode-se utilizar o sal nitrato de sódio (NaNO3), aumentando sua
temperatura de 300ºC para 550ºC, fazendo-se assim uma reserva para períodos sem
insolação. Essa energia armazenada poderá ser recuperada, com a temperatura do sal
retornando a 300ºC.
Para armazenar a mesma quantidade de energia que seria obtida com a queima de 1 L de
gasolina, necessita-se de uma massa de NaNO3 igual a
Dados:
Poder calórico da gasolina = 3,6×107 J/L
Calor específico do NaNO3 = 1,2×103 J/Kg ºC
a) 4,32 kg.
b) 120 kg.
c) 240 kg.
d) 3×104 kg.
e) 3,6×104 kg.
89. (Fuvest 2010) Uma determinada montagem óptica é composta por um anteparo,
uma máscara com furo triangular e três lâmpadas, L1, L2 e L3, conforme a figura a
seguir. L1 e L3 são pequenas lâmpadas de lanterna e L2, uma lâmpada com filamento
extenso e linear, mas pequena nas outras dimensões. No esquema, apresenta-se a
imagem projetada no anteparo com apenas L1 acesa.
Página 63 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
O esboço que melhor representa o anteparo iluminado pelas três lâmpadas acesas é
a)
b)
c)
d)
e)
90. (Unicamp 2010)
Há atualmente um grande interesse no desenvolvimento de
materiais artificiais, conhecidos como metamateriais, que têm propriedades físicas não
Página 64 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
convencionais. Este é o caso de metamateriais que apresentam índice de refração
negativo, em contraste com materiais convencionais que têm índice de refração
positivo. Essa propriedade não usual pode ser aplicada na camuflagem de objetos e no
desenvolvimento de lentes especiais.
a) Na figura a seguir é representado um raio de luz A que se propaga em um material
convencional (Meio 1) com índice de refração n1 = 1,8 e incide no Meio 2 formando um
ângulo 1 = 30° com a normal. Um dos raios B, C, D ou E apresenta uma trajetória que
não seria possível em um material convencional e que ocorre quando o Meio 2 é um
metamaterial com índice de refração negativo. Identifique este raio e calcule o módulo
do índice de refração do Meio 2, n2, neste caso, utilizando a lei de Snell na forma:
n1 senθ1  n2 senθ2. Se necessário use
2  1,4 e 3  1,7.
b) O índice de refração de um meio material, n, é definido pela razão entre as
velocidades da luz no vácuo e no meio. A velocidade da luz em um material é dada por
v
1
, em que å é a permissividade elétrica e ì é a permeabilidade magnética do
εμ
material.
Calcule
  2,0x1011
o
índice
de
2
C2
6 N.s
e


1
,25x10
.
N.m2
C2
refração
A
de
velocidade
um
da
material
luz
no
que
tenha
vácuo
é
c = 3,0×108 m/s.
Página 65 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
91. (Fuvest 2010) Luz proveniente de uma lâmpada de vapor de mercúrio incide
perpendicularmente em uma das faces de um prisma de vidro de ângulos 30o, 60o e 90o,
imerso no ar, como mostra a figura a seguir.
A radiação atravessa o vidro e atinge um anteparo.
Devido ao fenômeno de refração, o prisma separa as diferentes cores que compõem a
luz da lâmpada de mercúrio e observam-se, no anteparo, linhas de cor violeta, azul,
verde e amarela. Os valores do índice de refração n do vidro para as diferentes cores
estão dados adiante.
a) Calcule o desvio angular į, em relação a direção de incidência, do raio de cor
violeta que sai do prisma.
b) Desenhe, na figura da página de respostas, o raio de cor violeta que sai do prisma.
c) Indique, na representação do anteparo na folha de respostas, a correspondência entre
as posições das linhas L1, L2, L3 e L4 e as cores do espectro do mercúrio.
NOTE E ADOTE:
č
senč
Cor
N (vidro)
60
0,866
Violeta
1,532
50
0,766
Azul
1,528
40
0,643
Verde
1,519
30
0,500
amarelo
1,515
(graus)
lei de Snell:
n
=1
para
qualquer
n1 senč1 = n2 comprimento de onda no
Página 66 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
senč2
ar.
b)
c)
92. (Unicamp 2010) A experimentação é parte essencial do método científico, e muitas
vezes podemos fazer medidas de grandezas físicas usando instrumentos extremamente
simples.
a) Usando o relógio e a régua graduada em centímetros da figura a seguir, determine o
módulo da velocidade que a extremidade do ponteiro dos segundos (o mais fino) possui
no seu movimento circular uniforme.
b) Para o seu funcionamento, o relógio usa uma pilha que, quando nova, tem a
capacidade
de
fornecer
uma
carga
q = 2,4 Ah = 8,64×103 C. Observa-se que o relógio funciona durante 400 dias até que a
pilha fique completamente descarregada. Qual é a corrente elétrica média fornecida pela
pilha?
Página 67 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
93. (Fuvest 2010)
Medidas elétricas indicam que a superfície terrestre tem carga
elétrica total negativa de, aproximadamente, 600.000 coulombs. Em tempestades, raios
de cargas positivas, embora raros, podem atingir a superfície terrestre. A corrente
elétrica desses raios pode atingir valores de até 300.000 A. Que fração da carga elétrica
total da Terra poderia ser compensada por um raio de 300.000 A e com duração de 0,5
s?
a)
1
2
b)
1
3
c)
1
4
d)
1
10
e)
1
20
94. (Unicamp 2010) Telas de visualização sensíveis ao toque são muito práticas e cada
vez mais utilizadas em aparelhos celulares, computadores e caixas eletrônicos. Uma
tecnologia frequentemente usada é a das telas resistivas, em que duas camadas
condutoras transparentes são separadas por pontos isolantes que impedem o contato
elétrico.
Página 68 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
a) O contato elétrico entre as camadas é estabelecido quando o dedo exerce uma força F
sobre a tela, conforme mostra a figura a seguir. A área de contato da ponta de um dedo é
igual a A = 0,25 cm2. Baseado na sua experiência cotidiana, estime o módulo da força
exercida por um dedo em uma tela ou teclado convencional, e em seguida calcule a
pressão exercida pelo dedo. Caso julgue necessário, use o peso de objetos conhecidos
como guia para a sua estimativa.
b) O circuito simplificado da figura no espaço de resposta ilustra como é feita a
detecção da posição do toque em telas resistivas. Uma bateria fornece uma diferença de
potencial U = 6 V ao circuito de resistores idênticos de R = 2 kÙ. Se o contato elétrico
for estabelecido apenas na posição representada pela chave A, calcule a diferença de
potencial entre C e D do circuito.
95. (Fuvest 2010) Em uma aula de física, os estudantes receberam duas caixas lacradas,
C e C’, cada uma delas contendo um circuito genérico, formado por dois resistores (R1 e
R2), ligado a uma bateria de 3 V de tensão, conforme o esquema da figura a seguir.
Página 69 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Das instruções recebidas, esses estudantes souberam que os dois resistores eram
percorridos por correntes elétricas não nulas e que o valor de R1 era o mesmo nas duas
caixas, bem como o de R2. O objetivo do experimento era descobrir como as
resistências estavam associadas e determinar seus valores. Os alunos mediram as
correntes elétricas que percorriam os circuitos das duas caixas, C e C’, e obtiveram os
valores I = 0,06 A e I’ = 0,25 A, respectivamente.
a) Complete as figuras da folha de resposta, desenhando, para cada caixa, um esquema
com a associação dos resistores R1 e R2.
b) Determine os valores de R1 e R2.
NOTE E ADOTE:
Desconsidere a resistência interna do amperímetro.
96. (Unicamp 2010) Ruídos sonoros podem ser motivo de conflito entre diferentes
gerações no ambiente familiar.
a) Uma onda sonora só pode ser detectada pelo ouvido humano quando ela tem uma
intensidade igual ou superior a um limite I0, denominado limiar de intensidade sonora
audível. O limiar I0 depende da frequência da onda e varia com o sexo e com a idade.
Nos gráficos no espaço de resposta, mostra-se a variação desse limiar homens, I0H, e
para mulheres, I0M, em diversas idades, em função da frequência da onda.
Considerando uma onda sonora de frequência f = 6 kHz, obtenha as respectivas idades
de homens e mulheres para as quais os limiares de intensidade sonora, em ambos os
casos, valem I0H = I0M =10-11 W/m2.
b) A perda da audição decorrente do avanço da idade leva à utilização de aparelhos
auditivos, cuja finalidade é amplificar sinais sonoros na faixa específica de frequência
Página 70 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
da deficiência auditiva, facilitando o convívio do idoso com os demais membros da
família. Um esquema simplificado de um aparelho amplificador é representado a seguir.
Considere que uma onda sonora provoque uma diferença de potencial no circuito de
entrada do aparelho amplificador igual a Ve = 10 mV e que a diferença de potencial de
saída Vs é igual a 50 vezes a de entrada Ve.
Sabendo que a potência elétrica no circuito de saída é Ps = 0,3 mW calcule a corrente
elétrica is no circuito de saída.
97. (Unicamp 2010) O Efeito Hall consiste no acúmulo de cargas dos lados de um fio
condutor de corrente quando esse fio está sujeito a um campo magnético perpendicular
à corrente. Pode-se ver na figura (i) uma fita metálica imersa num campo magnético B ,
perpendicular ao plano da fita, saindo do papel. Uma corrente elétrica atravessa a fita,
como resultado do movimento dos elétrons que têm velocidade v , de baixo para cima
até entrar na região de campo magnético. Na presença do campo magnético, os elétrons
sofrem a ação da força magnética, FB , deslocando-se para um dos lados da fita. O
acúmulo de cargas com sinais opostos nos lados da fita dá origem a um campo elétrico
no plano da fita, perpendicular à corrente. Esse campo produz uma força elétrica FE ,
contrária à força magnética, e os elétrons param de ser desviados quando os módulos
Página 71 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
dessas forças se igualam, conforme ilustra a figura (ii). Considere que o módulo do
campo elétrico nessa situação é E = 1,0×10−4 V/m .
a) A fita tem largura L = 2,0 cm. Qual é a diferença de potencial medida pelo voltímetro
V na situação da figura (ii)?
b) Os módulos da força magnética e da força elétrica da figura (ii) são dados pelas
expressões FB = qvB e FE = qE , respectivamente, q sendo a carga elementar. Qual é a
velocidade
dos
elétrons?
O
módulo
do
campo
magnético
é
B = 0,2 T.
98. (Fuvest 2010) Aproxima-se um ímã de um anel metálico fixo em um suporte
isolante, como mostra a figura. O movimento do ímã, em direção ao anel,
a) n‫م‬o causa efeitos no anel.
b) produz corrente alternada no anel.
c) faz com que o polo sul do ímã vire polo norte e vice versa.
d) produz corrente elétrica no anel, causando uma força de atração entre anel e ímã.
e) produz corrente elétrica no anel, causando uma força de repulsão entre anel e ímã.
Página 72 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
99. (Fuvest 2010)
A figura a seguir mostra o esquema de um instrumento
(espectrômetro de massa), constituído de duas partes. Na primeira parte, há um campo
elétrico E , paralelo a esta folha de papel, apontando para baixo, e também um campo
magnético B1 , perpendicular a esta folha, entrando nela. Na segunda, há um campo
magnético, B2 de mesma direção que B1 , mas em sentido oposto. Íons positivos,
provenientes de uma fonte, penetram na primeira parte e, devido ao par de fendas
F1 e F2 , apenas partículas com velocidade v , na direção perpendicular aos vetores E e
B1 , atingem a segunda parte do equipamento, onde os íons de massa m e carga q tem
uma trajetória circular com raio R.
a) Obtenha a expressão do módulo da velocidade v em função de E e de B1.
b) Determine a razão m/q dos íons em função dos parâmetros E, B1, B2 e R.
c) Determine, em função de R, o raio R’ da trajetória circular dos íons, quando o campo
magnético, na segunda parte do equipamento, dobra de intensidade, mantidas as demais
condições.
NOTE E ADOTE:
Felétrica  q E (na direção do campo elétrico).
Fmagnética  q v B senθ (na direção perpendicular a v e a B ; θ e o angulo formado por
v e B ).
100. (Fuvest 2010)
Um estudo de sons emitidos por instrumentos musicais foi
realizado, usando um microfone ligado a um computador. O gráfico a seguir,
reproduzido da tela do monitor, registra o movimento do ar captado pelo microfone, em
função do tempo, medido em milissegundos, quando se toca uma nota musical em um
violino.
Página 73 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Nota
Frequência
(HZ)
dó
ré
mi
fá
sol
lá
si
262
294
330
349
388
440
494
Consultando a tabela acima, pode-se concluir que o som produzido pelo violino era o da
nota
Dado: 1 ms = 10-3 s
a) dó.
b) mi.
c) sol.
d) lá.
e) si.
Página 74 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Gabarito:
Resposta
da
questão
1:
[Resposta do ponto de vista da disciplina de Biologia]
a) No vaso 1, a planta cresce normalmente, pois consegue absorver os comprimentos de
onda equivalentes ao azul e ao vermelho. Esses comprimentos de onda tornam a taxa de
fotossíntese mais eficiente. A planta do vaso 2 reflete a radiação verde e não consegue
crescer devido à ineficiência de sua taxa fotossintética.
[Resposta do ponto de vista da disciplina de Física]
b) A cor de um objeto é a mesma cor da radiação que ele mais difunde (reflete).
Portanto, se as pessoas com visão normal enxergam as folhas como verdes, é porque
elas refletem com maior intensidade a radiação correspondente à luz verde.
Resposta
da
questão
2:
[B]
Resposta de Biologia: Em um ambiente de penumbra, ao focalizar um objeto próximo,
a íris do olho relaxa, aumentando o diâmetro da pupila. Os músculos ciliares que
prendem o cristalino se contraem, causando o aumento do poder refrativo da lente do
olho.
Resposta de Física: Da maneira como a questão está, não tem resposta. Do ponto de
vista físico, a segunda afirmativa está errada em todas as opções.
Quando o indivíduo passa para um ambiente de penumbra, a íris diminui, aumentando a
abertura da pupila para que os olhos recebam maior luminosidade. Correto. Porém, para
focalizar um objeto mais próximo, os músculos ciliares se contraem, aumentando a
curvatura do cristalino, diminuindo a sua distância focal para que a imagem caia na
retina. Não ocorre variação alguma no poder refrativo do cristalino. Para mudar o
poder refrativo de um sistema óptico é necessário que se mude a substância ou
material que o constitui.
Página 75 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
3:
a) Resposta de História. A primeira fase (“ascensão contínua”) corresponderia ao
processo de formação do sistema capitalista, época de acumulação primitiva de capitais
nos países centrais / metropolitanos europeus, e, consequentemente, de ascensão da
camada burguesa, que se consolidou no século XIX, com o controle político sobre os
Estados Nacionais.
A segunda fase (“queda vertiginosa”) corresponde ao momento das unificações
“tardias” de Itália e Alemanha, marcado por conflitos militares que envolveram diversos
povos e nações. Essas guerras colocaram em cheque o domínio da classe burguesa,
questionado por interesses nacionais específicos, percebidos no fortalecimento do
nacionalismo em diferentes países e no rompimento do frágil equilíbrio que havia entre
as nações europeias, que redundou na Primeira Guerra Mundial. Esse processo de crise
burguesa e capitalista foi acompanhado pelas duas grandes crises – depressões – vividas
pelo capitalismo (1873 e 1929), e pela Revolução comunista na Rússia, questionando
todo o sistema e o domínio da burguesia.
Por fim, a terceira fase (loop) é o atual momento, iniciado nos anos 80 do século
XX, marcado pelos avanços tecnológicos, em velocidade vertiginosa, o que faz com que
todos os avanços ocorridos em momentos anteriores pareçam “lentos”; e que são
acompanhados pela decomposição do “bloco socialista” e, portanto, pela concepção de
vitória do sistema capitalista, ao mesmo tempo em que a globalização e a
informatização se encarregam de romper barreiras econômicas.
b) Resposta de Física. 1. Pela figura dada, o ponto 2 situa-se no trecho retilíneo
destacado e ampliado na figura abaixo.
Usando o teorema de Pitágoras, calculemos L na Fig. 1:
Página 76 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
L2 = 32 + 102  L  109  L  10,44.
Nessa mesma figura:
cos  =
10
10,44

cos   0,96.
Na Fig. 2, notamos que no ponto 2 a resultante das forças sobre o carrinho é a
componente tangencial do peso Pt  . Dado g = 10 m/s2, sendo m a massa do carrinho e
v
a o módulo a aceleração de sua aceleração nesse ponto 2, temos:
Pt = m a  m gcos   m a  a  gcos   10 (0,96)  a  9,6 m/s2.
2. Dados: g = 10 m/s2; v1 = 0; h1 = 20 m, h3 = 16 m.
Pela conservação da energia mecânica:
EMec 1  EMec
3

v3  80 m/s

Resposta
m v 32
 m g h3
2
v 3  8,9 m/s.
m g h1 

da
v 3  2 g h1  h3   2 10  4 
questão

4:
a) Como não foi especificado velocidade escalar média, trata-se de velocidade vetorial
média, pois velocidade é uma grandeza vetorial.
A figura mostra o deslocamento vetorial (d) entre os pontos A e B.
O módulo (d) desse deslocamento é:
Página 77 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
d2  402  302  d  50 μm  50  106 m.
Na figura dada, contamos 10 deslocamentos sucessivos entre A e B. Assim:
Δt  10  30  Δt  300 s.
Então:
vm 
d 50  106

 vm  1,67  107 m/s.
Δt
300
b) Dados: I  2 D t; D  kT r; k  3 1018 m3 sK; r  3 μm  3 106 m; T  300 K;
Δt  10 min  600 s.
Combinando as expressões dadas e substituindo os valores, vem:
I 2
kT
t  I
r
2
Resposta
3  1018  300
3  106
 600 
I  6  104 m.
da
questão
5:
[B]
Dados: vA = 5 m/s; vB = 26 nós; 1 nó = 0,5 m/s; d = 40 km.
O módulo da velocidade do barco é:
vB  26  0,5  13 m / s.
Se o barco navega rio acima, a velocidade resultante tem módulo igual à diferença dos
módulos:
v  vB  v A  13  5  v  8 m / s  8 3,6  km / h 
v  28,8 km / h.
Aplicando a definição de velocidade escalar:
d
d
40
40
 t  
h  t 
 60min  83,33min 
t
v 28,8
28,8
t  1 h e 23min.
v
Resposta
da
questão
6:
a) Dados: R = 6.800 km; f = 16 voltas/dia = 2/3 volta/hora; π  3.
Da expressão da velocidade para o movimento circular uniforme:
Página 78 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
v  2πRf  2  3  6.800 
2
 v  27.200 km / h.
3
b) m  90 toneladas  9 104 kg;v  8 103 m / s.

4
3
mv2 9  10  8  10
EC 

2
2

Resposta
2
 EC  2,88  1012 J.
da
questão
7:
[B]
OBS: Essa questão foi cobrada na prova de Matemática, mas admite solução através de
conceitos Físicos, aliás, solução bem mais simples e curta. Serão dadas aqui as duas
soluções.
1ª Solução (Matemática):
Encontremos, primeiramente, a equação da parábola que passa pelos pontos dados:
A equação reduzida da parábola de raízes x1 e x2 é: y  a  x  x1  x  x2 .
Nesse caso temos: x1 = 0 e x2 = 40.
Substituindo esses valores na equação dada:
y  a  x  0  x  40   y  ax 2  40ax.
Para x = 30  y = 3. Então:
3  a 30  40a 30  3  900a  1200a  a  
2
1
.
100
Página 79 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Assim, a equação da parábola mostrada é:
y
x2
x2 2
 1 
 40 
x

y


 x.

100
100 5
 100 
Para x = 20  h = H. Então:
H
 202  2
100
H  4 m.
5
 20
 H  4  8 
2ª Solução (Física):
Pela regra de Galileu, sabemos que, para qualquer movimento uniformemente variado
(M.U.V.) com velocidade inicial nula, os espaços percorridos em intervalos de tempo
(t) iguais e subsequentes, as distâncias percorridas são: d, 3d, 5d, 7d...
Ora, a queda livre e o lançamento horizontal na direção vertical são movimentos
uniformemente variados a partir do repouso, valendo, portanto a regra de Galileu.
Assim, se a distância de queda num intervalo de tempo inicial (t) é h, nos intervalos
iguais e subsequentes as distâncias percorridas na queda serão: 3h, 5h, 7h...
O lançamento oblíquo, a partir do ponto mais alto (A), pode ser considerando um
lançamento horizontal. Como a componente horizontal da velocidade inicial se mantém
constante (vx = v0x), os intervalos de tempo de A até B e de B até C são iguais, pois as
distâncias horizontais são iguais (10 m).
Assim, se de A até B a bola cai h, de B até C ela cai 3h, como ilustrado na figura.
Então:
Página 80 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
3h  3  h  1 m.
Mas : H  3h  h  3  1  H  4 m.
3ª Solução (Física):
Como as distâncias horizontais percorridas entre A e B e entre B e C são iguais, os
intervalos de tempo entre esses pontos também são iguais, pois a componente horizontal
da velocidade se mantém constante (vx = v0x). Assim, se o tempo de A até B é t, de A até
C é 2t.
Equacionando a distância vertical percorrida na queda de A até B e de A até C, temos:

g 2
A  B : h  2 t


A  C : H  g  2t 2

2
g 
 H  4  t2 
2 
 H  4h.
Mas, da Figura: H  h  3  4h  h  3  h  1 m.
Como H  4h  H  4 m.
Resposta
da
questão
8:
Dados: R = 20 m; MN = 60 kg; MJ = 70 kg.
a) Como as posições se invertem em 15 s, antes de a roda completar uma volta, esse
intervalo de tempo corresponde a meio período.
T
 15  T  30 s.
2
O módulo da velocidade linear das cadeiras é:
Página 81 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
v
2πR 2 3 20

T
30
 v  4 m / s.
b) A aceleração radial é a aceleração centrípeta:
aR 
v2 42

R 20
 aR  0,8 m / s2.
c) A figura ilustra a situação descrita:
Como se trata de movimento circular, a resultante (R) é centrípeta, ou seja, dirigida para
o centro.
Para Nina:
PN  NN  RN  NN  MN g  MN aR  NN  60 10  0,8  
NN  552 N.
Para José:
NJ  PJ  RJ  NJ  MJ aR  MJ g  NN  70 10  0,8  
NJ  756 N.
Resposta
da
questão
9:
[E]
Analisando cada uma das afirmações:
I. Incorreta. Quando menor o ângulo  , mais inclinada está a pessoa, exigindo maior
Página 82 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
esforço da coluna, portanto menor o peso que se consegue levantar.
II. Correta. Quanto maior o ângulo  , mais ereto está o halterofilista, exigindo menor
esforço da coluna.
III. Correta. Quanto maior o valor de  , menor a tensão na musculatura eretora ao se
levantar um peso, que é exatamente o que mostra o gráfico.
Resposta
da
questão
10:
Dados:
P  0,1 A  v3 ; A  2m2; v  5m / s; h  7,5m; g  10m / s2;   1g / cm3  1kg / L  103 kg / m3 .
a) Para essa velocidade do vento, a potência P1 é:
P1  0,1 2 5 
3
 P1  25 W.
b) Como a densidade da água é 1 kg/L, a massa de 1 L é m = 1 kg.
E  mgh  110  7,5   E  75 J.
c) Como a potência é constante, da definição de potência média:
P1 
E
t1
 t1 
E 75

 t1  3 s.
P1 25
Nesse intervalo de tempo, o volume bombeado é V = 1 litro de água. Então, a vazão z1
é:
z1 
V 1
1

 z1  L / s.
t1 3
3
Assim, o volume de água bombeado a cada segundo é V1 = 1/3 L.
d) Se a velocidade do vento cair pela metade, a nova potência útil é:
3
25
5
P2  0,1 2    P2 
W.
8
2
E
E
75
P2 
 Δt2 

 Δt1  24 s.
Δt2
P2 25
8
A nova vazão é z2:
Página 83 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
z2 
V
1
1

 z2 
L / s.
t2 24
24
Assim, o volume de água bombeado a cada segundo é V2 = 1/24 L.
Resposta
da
questão
11:
a) No gráfico, nota-se que a partir da velocidade de 8,5 km/h (ponto onde a curva cheia
e a pontilhada se cruzam) ele gasta mais energia andando que correndo.
b) Também no gráfico, para a velocidade de 0,0 km/h (atleta parado) o consumo de
oxigênio é de 0,2 / min. Se, para cada litro de oxigênio consumido, ele gasta 5 kcal,
então para 12 h de repouso a quantidade de energia (E) por ele gasta é:


 min   kcal 
C  0,2 
 12 h  60 

  5
  E  720 kcal.
 min 
 h  

c) P 

  kcal 
 J 
 J
 P  3,6 
  5
  4.000  kcal   1.200  s   P  1.200W.
60
s



 

 
E
Δt
d) Ainda do gráfico, andando (curva cheia) a 7 km/h o consumo de oxigênio é de
1,6 / min.
E
560

  kcal 
 E  P Δt  560  1,6 
 5
 Δt  Δt 


Δt
8
 min  

Δt  70min.
P
Resposta
da

questão
12:
a) Dados: V20  4 L;r20  0,882 kg / L;r100  0,840 kg / L.
Como a massa não se altera:
m20  m100  ρ20 V20  ρ100 V100  0,882  4   0,84 V110 
V100  4,2 L.
b) Dados: Fatrito  3,0 N;d  12 cm  0,12 m;n  2.500 ciclos;Dt  1 min  60 s.
Da expressão da potência média:
Pdissip 
WFat n Fatrito d 2.500(3)(0,12)


 Pdissip  15 W.
Δt
Δt
60
Resposta
da
questão
13:
Página 84 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
[D]
EP  mgh  1,2  104  10  25  3  106 J.
Resposta
da
questão
14:
[C]
Inicialmente, a temperatura da sala diminui. Uma vez atingido o equilíbrio térmico, a
temperatura da sala aumenta, pois está entrando energia elétrica na sala, sendo
transformada em energia térmica pelo sistema motor-compressor.
Resposta
da
questão
15:
a) Dados: V  3 106L  3 103 m3; g  10 m / s2; ρamb  1,26 kg / m3.
Da expressão do empuxo:
E  ρamb V g  1,26  10  3  103  E  3,78  104 N.
b) Dados: ρamb  1,26 kg / m3 ; ρquente  1,05 kg / m3; Pquente  Pamb ; Vquente  Vamb .
Da equação de Clapeyron:
PV
 R (cons tante).
nT
PV  nRT 
Então:
Pquente Vquente
nquenteTquente
nquente
namb

Pamb Vamb
namb Tamb
 nquente Tquente  namb Tamb 
Tamb
.
Tquente

Mas o enunciado afirma que o número de mols de ar no interior do balão é proporcional
à sua densidade. Então:
nquente
namb

ρquente
ρamb

Tamb
Tquente

1,05
300

1,26 Tquente
 Tquente 
1,26  300
1,05

Tquente  360 K.
Resposta
da
questão
16:
Página 85 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
[D]
Antes de jogar a bola, Maria e a bola estão em repouso, portanto a quantidade de
movimento desse sistema é nula. Como o sistema é mecanicamente isolado (a resultante
das forças externas é nula), apliquemos a ele a conservação da quantidade de
movimento:
Qsist antes  Qsistema depois
VMaria 
 0  m v  M VMaria 
 M VMaria  m v 
m v
.
M
Antes de agarrar a bola que tem velocidade v, Luísa tem velocidade -V. Aplicando
novamente a conservação da quantidade de movimento:
Qsist antes  Qsist depois
VLuísa 
 m v  M V  m  M VLuísa 
m v M V
mM
Resposta
da
questão
17:
[D]
OBS: o Note e Adote traz uma informação errada:   Vf 2 / Vi2 . A expressão correta do
coeficiente de restituição é:   Vf / Vi .
Faremos duas soluções, a primeira usando a expressão errada do coeficiente de
restituição e a segunda, usando a expressão correta.
1ª Solução:
Dados: hi = 1 m;

vi2
 0,8.
v 2f
Desprezando a resistência do ar, a velocidade final de uma colisão é igual à velocidade
inicial da próxima. As figuras mostram as velocidades inicial e final, bem como as
Página 86 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
alturas inicial e final para cada uma das três colisões.
Aplicando a equação de Torricelli antes e depois de cada colisão:
v 2  2ghi
h
v2
h1
1ª  i2
  1  12  0,8 
 0,8 (I).
hi vi
hi
v1  2gh1
v 2  2gh1
h
v2
h2
2ª  12
  2  22  0,8 
 0,8 (II).
h1 v1
h1
v 2  2gh2
2
h
v2
hf
v  2gh2
3ª  22
  f  2f  0,8 
 0,8 (III).
h2 v 2
h2
v f  2ghf
Multiplicando membro a membro (I), (II) e (III):
h1 h2 hf
3
 
 0,8  0,8  0,8   0,8 
hi h1 h2
hf  0,51 m.

hf
 0,512 
hi
hf
 0,512 
1
2ª Solução:
Dados: hi = 1 m;

vi
 0,8.
vf
As figuras mostram as velocidades inicial e final, bem como as alturas inicial e final
para cada uma das três colisões.
Página 87 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Aplicando a equação de Torricelli antes e depois de cada colisão:
2
v 2  2ghi
h
v2
h v 
h
2
2
1ª  i2
  1  12  1   1   0,8   1  0,8  (I).
h
h
h
v
v
i
i
i
i
 i 
v1  2gh1
2
v 2  2gh1
h
v2
h2  v 2 
h2
2
2
2ª  12
  2  22 
     0,8  
 0,8  (II).
h1 v1
h1  v1 
h1
v 2  2gh2
2
2
h
v2
hf  v f 
hf
2
2
v  2gh2
3ª  22
  f  2f 
     0,8  
  0,8  (III).
h2 v 2
h2  v 2 
h2
v f  2ghf
Multiplicando membro a membro (I), (II) e (III):
h1 h2 hf
6
 
 0,82  0,82  0,82   0,8 
hi h1 h2
hf  0,26 m.

hf
 0,262 
hi
hf
 0,262 
1
Nesse caso, resposta mais próxima é 0,20, que está na opção E.
Resposta
da
questão
18:
a) Dados: M  9.000 kg;V  80 km / h;ma  1.000 kg;v a  0.
O Sistema é mecanicamente isolado. Então, ocorre conservação da quantidade de
movimento na colisão.
depois
Qantes
 MV  mava  M  m v  9.000(80)  10.000v 
sist  Qsist
v  72 km / h.
b) Dados: mb  1.600 kg;sen3°  0,05;cos3°  0,99; Fat  8.000 N.
Da figura dada:
F
sen3  L
Fat
 0,05 
FL
 FL  400 N.
8.000
Página 88 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Aplicando o princípio fundamental da dinâmica na direção lateral:
FL  maaL  400  1.600 aL  aL  0,25 m / s2.
OBS: A questão foi resolvida de forma fiel ao enunciado. No entanto, pode se
questionar se o aparecimento dessa força lateral numa roda desalinhada não provoca
outra força de atrito em sentido oposto na outra roda dianteira, impedindo que o carro
desvie lateralmente, sendo, então, nula a aceleração lateral do carro. A experiência de
motorista mostra que um carro desalinhado somente desvia quando se solta o volante.
Resposta
da
questão
19:
[A]
Dados: mS = 20 g = 2010–3 kg; mS = 30 g = 3010–3 kg; mS = 70 g = 7010–3 kg; g =
10 m/s2.
1ª Solução:
Podemos pensar de uma maneira simples:
– Se cortarmos o fio superior, os três elefantes cairão. Logo, a tração nesse fio superior
equilibra os pesos dos três elefantes. Sendo TS a tensão nesse fio, temos:
TS  PC  PM  PB  mC  mM  mB  g   20  30  70  103  10 
TS  1,2 N.
– Se cortarmos o fio médio, cairão os elefantes do meio e de baixo. Logo, a tração nesse
fio do meio equilibra os pesos desses dois elefantes. Sendo TM a tensão nesse fio,
temos:
TM  PM  PB  mM  mB  g  30  70   103  10 
TS  1,0 N.
– Analogamente, se cortarmos o fio inferior, cairá apenas o elefante de baixo. Logo, a
tração nesse fio equilibra o peso desse elefante. Sendo TB a tensão nesse fio, temos:
Página 89 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
TB  PB  mB g  70  103  10 
TB  0,7 N.
2ª Solução:
Racionando de uma maneira mais técnica, analisemos o diagrama de forças sobre cada
móbile.
De Cima (C)
Do Meio (M)
De Baixo (B)
Como se trata de um sistema em equilíbrio, a resultante das forças em cada elefante é
nula. Assim:
(C)  TS  PC  TM  0

(M)  TM  PM  TB  0
(B)  T  P  0
B
B

+
 TS  PC  PM  PB  0  TS  PC  PM  PB 
TS   20  30  70   103   10  TS  120  102 
TS  1,2 N.
Em (B):
TB  PB  0  TB  PB  70  103  10 
TB  0,7 N.
Em (M):
TM  PM  TB  0  TM  PB  TB  30  70   103   10 
TB  1,0 N.
Resposta
da
questão
20:
[C]
Página 90 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Dados: L0 = 30 cm;  = 210–6 °C-1;  0 = 25 °C; q = 225 °C; R = 10 cm; r = 2 cm.
Calculando a dilatação (d) da barra:
d  L0   30  2  105   225  25  d  0,12 cm  d  1,2 mm.
Pela figura abaixo, vemos que o deslocamento da extremidade superior (D) é
diretamente
proporcional
D R
D 10



d r
1,2 2
D  6 mm.
 D
ao
12
2
Resposta
da
extremidade
inferior
(d).

da
questão
21:
a) Dado: N0 = 9104.
Do gráfico, para θ  72 C  τ  5 s; t  1 s.
Aplicando a expressão fornecida no enunciado, calculamos o número de células que
permanecem vivas nos primeiros instantes.
 2t 
 2(1) 
4
4
N(t)  N0 1    9  104 1 
  9  10  0,6   N(t)  5,4  10 .
τ
5




O número de células que morrem (N’(t)) é:
N'(t)  N0  N(t)  9,0 104  5,4 104  N'(t)  3,6 104.
b) Dados: V  35 mL  35  103 L; Vmolar  28 L / mol; Δθ  72 – 37  35C; C  32
J
.
K  mol
Calculando o número de mols:

 1 mol
28 L

3
 n mol

35  10
 n
35  103
28
 n  1,25  103 mol.
Página 91 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
A quantidade de calor transferido ao fumante é dada pela equação do calor sensível na
forma molar.
Q  nC Δθ  1,25  103  32  35  Q  1,4 J.
Resposta
da
questão
22:
[C]
Obs:
1ª) pela simbologia adotada, conclui-se tratar-se de um espelho plano.
2ª) Para ver os pontos, o motorista teria que olhar para o lado esquerdo ou para trás.
Corretamente, a última linha do enunciado deveria ser: “Nesse caso, os pontos cujas
imagens podem ser vistas pelo motorista são:”
Assim entendendo, vamos à resolução:
– por simetria, encontra-se o ponto imagem dos olhos do observador;
– a partir desse ponto, passando pelas bordas do espelho, traçamos as linhas que
definem o campo visual do espelho;
– Serão vistas as imagens dos pontos que estiverem nesse campo, ou seja: 1, 2, 5 e 9.
A figura ilustra a solução:
Página 92 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
23:
a) A imagem é sempre simétrica do objeto. Para o observador, é como se o raio de luz
viesse da imagem.
b) Dado: y = 1 m.
Analisemos a figura a seguir.
Página 93 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Os triângulos GCP’ e GMN são semelhantes:
H y
H


 1  H  2 m.
2d d
2
c) Dado: h = 1,60 m
Na mesma figura do item anterior, os triângulos NQP’ e GPP’ são semelhantes:
Y h
h 1,6

 Y 
d 2d
2 2
 Y  0,8 m.
d) Conforme pôde se verificar nos itens [B] e [C] o tamanho mínimo do espelho e a
distância da base do espelho ao chão não dependem da distância (d) do rapaz ao
espelho.
Portanto: y’  y  1 m e Y’  Y  0,8 m.
Resposta
da
questão
24:
[E]
Basta calcularmos o ângulo limite, que é o ângulo de incidência (  ) no meio mais
refringente (núcleo) que provoca uma emergência rasante (90°) no meio menos
refringente (revestimento).
Dados: nnúcleo = 1,60; nrevest = 1,45.
Aplicando a lei de Snell:
nnúcleo sen  nrevest sen90  sen 
nresvest 1,45

 sen  0,91.
nnúcleo 1,60
Consultando a tabela dada:  = 65°.
Página 94 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
25:
Dados:
e  1,6  1019 C; U  64 mV  64  103 V; d  8 nm  8  109 m; C  12  1012 F; C 
Q
.
V
a) Sabemos que cargas negativas tendem para pontos de maior potencial elétrico e
cargas positivas tendem para pontos de menor potencial elétrico. Assim, os íons de
Cloro (C  ) movem-se de dentro para fora da célula e os íons de cálcio (Ca ) movemse em sentido oposto, de fora para dentro da célula.
b) Como o potencial elétrico varia linearmente com a distância, o campo elétrico ao
longo da membrana da célula é constante. Sendo U a ddp entre o interior e o exterior da
célula, da expressão do campo elétrico uniforme vem:
E dU  E
U 64  103

d 8  109
 E  8  106 V/m.
c) Os íons de cloro têm um elétron em excesso, portanto sua carga é
qC  e  1,6  1019 C. Os íons de cálcio têm valência +2, portanto têm carga
qCa  2e  3,2 1019 C. Da expressão da força elétrica:
FC  qC E  1,6  1019  8  106  FC  1,28  1012 N.
FCa  qCa E  3,2  1019  8  106  FC  2,56  1012 N.
d) Do gráfico, o potencial no interior da célula é nulo. Então, U  V  64 103 V.
C
Q
V
 Q  CV  12  1012  64  103  Q  7,68  1013 C.
Resposta
da
questão
26:
a) Dados: e  1,6 1019 C; A  5 105 cm2; U  80 mV  8 102 V; Cárea  0,8 106F / cm2.
A capacitância da membrana é o produto da capacitância por unidade de área pela área
da membrana.
 F 
  5  105 cm2
C  Cárea A  0,8  106 
 cm2 


 
 C  4  1011 F.
Página 95 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE

Q
C 
U

Q  ne

 C
ne
U
 n
C U 4  1011  8  102

e
1,6  1019

n  2,0  107 íons.
b) Dados: e  1,6 1019 C; z  5 108íons / s; U  20 mV  2 102 V.
 íons 
 C 
P  Ui  P  U z e  2  102  V   5  108 
1,6  1019 

 
 s 
 íon 
P  1,6  1012 W.
Resposta
da
questão
27:
a) A energia total consumida é o somatório das energias consumidas pelos aparelhos.
Da expressão da potência:
E
12
 E  P Δt  990  980  2  60  W  3h  4.400W  h  E  7.150 Wh 
Δt
60
E  7,15 kWh.
P
b) A figura a seguir mostra um esquema simplificado desse circuito, representando as
tomadas como fontes de corrente contínua e todos os dispositivos como resistores.
Da expressão da potência elétrica:
PU i  i
P
U
Apliquemos essa expressão em cada dispositivo e a lei dos nós em A, B e C no circuito
primário.
Página 96 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Nó A: i1  iC  iA 
4.400 990

 20  9  i1  29A.
220 110
Nó C: i2  iC  2iL  iF 
4.400
60 980
12 98
110
2

 20 

 20 
 i2  30A.
220
110 110
11 11
11
c) Nó B: iN  i1  i2  iN  29  30  iN  1 A.
Resposta
da
questão
28:
[B]
A potência transmitida é a mesma nos dois casos:
P1  P2  U1 i1  U2 i2 
i2 U1 750
i


 2  25.
i1 U2
30
i1
Considerando que a resistência elétrica seja a mesma para as duas correntes, as
potências elétricas dissipadas por efeito Joule nos dois casos são:
2
Pd1  R i12
Pd2 i22  i2 
  
  

2
Pd1 i12  i1 
Pd2  R i2
E2  625 E1.
Resposta

Pd2
Pd1
  25 
2
da
 Pd2  625 Pd1 
questão
29:
[A]
Figura I: linhas de campo eletrostático – placa plana eletrizada positivamente.
Figura II: linhas de campo eletrostático – duas partículas eletrizadas positivamente.
Figura III: linhas de campo magnético – espira percorrida por corrente elétrica.
Figura IV: linhas de campo magnético – fio reto percorrido por corrente elétrica.
Resposta
da
questão
30:
a) Dado: π  3 ; TR = 0,5 s; R = 50 cm; r = 0,8 cm.
ωR 
2π 2  3

 ωR  12 rad / s.
TR
0,5
Como não há escorregamento relativo entre a roda e o eixo do dínamo, ambos têm
mesma velocidade linear. Então:
Página 97 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
vD  vR  ωD r  ωR R  ωD 
ωR R
r

12  50 
0,8
 ωD  750 rad / s.
b) Usando novamente a expressão que relaciona o período de rotação e a velocidade
angular:
ωD 
2π
T
 T
2π 2  3

 T  8  103 s.
ωD 750
c) Dados: P = 24 W; R  6Ω .
P
ε2
R
 24 
ε2
6
 ε2  144  ε  12 V.
Resposta
da
questão
31:
[B]
Analisando cada afirmação:
I. Incorreta. De acordo com a expressão dada: v 
T
.

Se as cordas são idênticas, as densidades lineares são iguais, como as trações são
diferentes, as velocidades de propagação são diferentes. Na corda mais tracionada a
velocidade é maior.
II. Correta. Nas duas cordas o comprimento de onda é  = 4 m.
III. Incorreta. De acordo com a equação fundamental:
v
v  f  f  . Se as velocidades de propagação são diferentes e os comprimentos de

onda são iguais, as frequências são diferentes.
Resposta
da
questão
32:
a) Dados: c  3 108 m / s; λ / 2  L  λ  2L.
Da equação fundamental da ondulatória:
c
cλ f  f  .
λ
Página 98 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Essa expressão nos mostra que a menor frequência que a antena consegue sintonizar
corresponde ao maior comprimento de onda. Como, λ  2L , o comprimento de onda
máximo corresponde à haste de maior comprimento, indicada na figura, conforme exige
o enunciado.
Então:
λmáx =2 L  2 0,3   0,6 m.
fmín 
c
λmáx

3  108
0,6
 fmín  5  108 Hz.
b) Dados: k  2,25; k  n2; c  3 108 m / s; f  400 MHz  4 108Hz; v  c / n.
k  n2  2,25  n2  n  1,5.
v  λ f
c

 λ f

c
n
v


n

λ  0,5 m.
Resposta
 λ
c
3  108
3


n f 1,5  4  108 6
da

questão
33:
a) Dados: h = 6,610-34 Js; E = h ν.
Página 99 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
De acordo com o obtido na expressão abaixo  Eelét  h  , a energia é inversamente
λ

c
proporcional ao comprimento de onda. Conforme indica a figura, o menor comprimento
de onda é 3010-12 m.
Eelét  Efóton  h ν


c
c  λ ν  ν  λ

 Eelét  h
c
3  108
 6,6  1034
λ
30  1012

Eelét  6,6  1015 J.
b) Dados: λ  2L  L  λ /2; λ  0,15nm  0,15 109 m; sen 14,5  0,25 e cos 14,5  0,97.
Da figura dada:
sen θ 
λ
L
λ
λ
 2  senθ 
 d
.
d d
2d
2 senθ
Substituindo valores:
d
0,15  109
2  0,25
 d  3  1010 m.
Resposta
da
questão
34:
a) Dados:   300nm  3 107 m; c  3 108 m / s
Da equação fundamental da ondulatória:
cλ f  f 
c 3  108

λ 3  107
 f  1015 Hz.
Página 100 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Dado: h  4  1015 eV.s.
Da equação de Planck:
E  h f  E  4 1015 1015  E  4 eV.
c) Dado: W = 2,3 eV.
De acordo com o enunciado:
Ec  E  W  4  2,3  EC  1,7 eV.
d) Para a frequência f0 não mais são ejetados elétrons, ou seja, a energia cinética é nula.
0  E  W  E  W  2,3 eV.
Usando novamente a equação de Planck:
W  h fo  f0 
W
2,3

h 4  1015
Resposta
 f  5,75  1014 Hz.
da
questão
35:
[D]
Lembrando que cos 120° = -0,5, aplicando a lei dos cossenos na figura abaixo,
calculamos D:
D2  R2J  R2T  2RJRT cos120º  D2  RJ2  RT2  2RJRT (0,5) 
D  R2J  RT2  RJRT .
Resposta
da
questão
36:
[C]
Dados: RT = 1,51011 m; RJ = 7,51011 m.
Página 101 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
O período de revolução da Terra é TT = 1 ano terrestre.
Aplicando a expressão dada para a terceira lei de Kepler:
3
2
 RJ 
 TJ 

   

R
 TT 
T


3
2 
7,5  1011 
T 
  J 

 1,5  1011 
 1


 TJ2  53  TJ  125  11,2.
Entre as opções dadas, a resposta mais próxima é: TJ  12 anos terrestres.
Resposta
da
questão
37:
[B]
Dados: mT = 6,01024 kg; mJ = 2,01027 kg; RT = 1,51011 m; RJ = 7,51011 m; G =
6,710–11 Nm2/kg2.
No momento de maior proximidade, a distância entre os dois planetas é:
r  RJ  RT  7,5  1011  1,5  1011  r  6  1011 m.
Substituindo os valores na fórmula da força gravitacional:
FG
mTmJ
r2
 F  6,7  1011
6  1024  2  1027
6  10 
11 2

8  1041
36  1022

F  2,2  1018 N.
Resposta
da
questão
38:
questão
39:
[C]
Da definição de corrente elétrica:
Q
Q 0,8 Ah
 t  
 0,25 h  0,25  60 min 
t
im 3,2 A
t  15 min.
im 
Resposta
da
a) Dados: pG = 1,0  104 kcal/kg; pA = 7,0  103 kcal/kg; dG = 0,7 g/cm3 = 0,7 kg/L; dA
= 0,8 g/cm3 = 0,8 kg/L.
Página 102 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Calculando a massa correspondeste ao volume de 1 litro, para os dois
combustíveis:
mG = dG V = 0,7 (1)  mG = 0,7 kg;
mA = dA V = 0,8 (1)  mA = 0,8 kg.
Calculando a energia liberada por litro, para os dois combustíveis:
EG = mG pG = 0,7 (1,0  104)  EG = 7,0  103 kcal.
EA = mA pA = 0,8 (7,0  103)  EA = 5,6  103 kcal.
b) O enunciado afirma (na tabela) que a distância percorrida (D) é diretamente
proporcional à energia liberada pelo combustível consumido. Então:
DA DG

EA EG

DA
10

3
5,6  10
7  103

DA  8 km.
c) Dado: PG = R$ 2,40.
O preço máximo do álcool (Pm) acima do qual não seria mais conveniente usar
álcool é aquele que proporciona a mesma razão entre o preço e a distância percorrida
relativamente a gasolina.
Assim:
Pm PG

DA DG

Pm 2,40

8
10

Pm  R$ 1,92.
d) Dado: PA = R$ 1,60.
G=
Resposta
PA 1,60

DA
8

G = R$ 0,20.
da
questão
40:
a) Dados: R = 20 m; T = 240 s.
A Fig. 1 mostra a roda gigante e as posições da criança em cada um dos instantes
citados.
No gráfico a) estão assinalados esses pontos.
Página 103 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Para traçar a curva do gráfico a), vamos encontrar a função que fornece a altura
em função do tempo [h = f(t)].
Novamente na Fig.1 notamos que:
h  R  Rcos   h  R 1  cos  
h  20 1  cos  (I).
Mas:
 = t   =
2
2

t =
t =
t (II).
T
240
120
Substituindo (II) em (I):
 

h  20 1  cos
t .
120 

A partir dessa função, obtemos a tabela abaixo para a construção do gráfico. A
curva tem forma senoidal.
t(s)
h(m)
0
0,0
30
5,9
60
20
90
34,1
120
40
150
34,1
180
20
Página 104 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
210
5,9
240
0
b) Dados: R = 4 m;  = 3.
Estimando um período de 20 s para o movimento do carrossel, temos:
0 
2 2  3

T
20

0  0,3 rad/s.
Como se trata de movimento circular uniforme, a aceleração centrípeta tem
módulo constante. Calculando-o:
ac = 02 R   0,3  4  ac = 0,36 m/s2 (constante). Assim, o gráfico é um
2
segmento de reta horizontal.
Resposta
da
questão
41:
a) Dados: h = 32 m; v0 = 72 km/h = 20 m/s; [ h  d tg  5  d² / v02  (1 + tg2  )].
Como a bola cai exatamente no pé do companheiro, h = 0.
Substituindo esses valores na expressão dada:
 322 
0  32 tg  5  2  1  tg2
 20 
2
12,8 tg   32 tg  12,8  0.




0  32 tg  12,8 1  tg2


Dividindo por 12,8, vem:
tg2 – 2,5 tg  + 1 = 0.
Resolvendo a equação do 2º grau:
Página 105 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
tg 
2,5  2,52  4 11
2

tg  2.
2,5  1,5  1
tg 

1
2
tg2  2 .
4
5
A
b) Dados: FCinicial
 FCBinicial =150 bpm; FCB  150 bpm ; VSA  VSB
Calculando a variação do débito cardíaco de B:
DC
 DCBinicial  VSB FCBfinal  FCBinicial  VSB 150  120  
DC
 DCBinicial  30 VSB .
B
final
B
final




A variação do débito cardíaco de A é:
DC
A
final





A
A
A
 DCinicial
 VSA FCfinal
 FCinicial
 VSA FCAfinal  120 .
4
5
Como as variações são iguais e VSA  VSB , temos:


4 B
A
VS FCfinal
 120  30 VSB 
5
A
FCfinal
 157,5 batimentos
.
minuto
Resposta
da
5
A
FCfinal
 30  120
4

questão
42:
Dados: mA = 0,5 kg; mB = 1 kg;  = 0,3; k = 10 N/m; x0 = 10 cm = 0,1 m; t = 2 min =
120 s;
v = 0,1 m/s (constante).
A figura abaixo ilustra as forças (ou componentes de forças) relevantes atuantes nas
partes A e B, respectivamente.
v
v
PA e PB  pesos.
v
v
NA e NB  componentes normais.
v
v
fA e fB  componentes de atrito.
v
v
FA e FB  forças elásticas.
Página 106 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
a) Como o movimento é retilíneo e uniforme, a resultante das forças no brinquedo, ou
em cada uma das partes, é nula. Assim:
T – fA – fB = 0  T –  (NA + NB) = 0  T –  (mA + mB) g = 0  T – 0,3 (1,5)
10 = 0 
T = 4,5 N.
b) W = T S = T v t  W = 4,5 (0,1) (120)  W = 54 J.
c) Na parte A:
FA – fA = 0  FA –  NA = 0  FA –  mA g = 0  FA – 0,3 (5) = 0  FA = 1,5
N.
Mas:
FA = FB = F  F = 1,5 N.
d) Da lei de Hooke:
FA = k x  FA = k (x – x0)  1,5 = 10 (x – 0,1)  0,15 = x – 0,1 
x = 0,25 m = 25 cm.
Resposta
da
questão
43:
[A]
Pelo teorema da energia cinética, o trabalho da resultante ( WR ) das forças que atuam
sobre um corpo é igual à variação da energia cinética do corpo. Como a velocidade é
constante, esse trabalho é nulo.
Página 107 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
44:
a) Dados: v = 72 km/h = 20 m/s; m = 70 kg; t = 0,1 s; v’ = 0.
Como a força pedida é a resultante, podemos usar o Teorema do Impulso.
v
v
I Rv  Q

F t  m v
 F
m v 70  20 

t
0,1

F  14.000 N.
b) Dados: E = 12 kJ = 12  103 J; m = 60 kg.
EP = E  m g h = E  h 
Resposta
E
12.000

m g 60 10 
 h  20 m.
da
questão
45:
[E]
Dados: h = 2,4 m; vAB = 4 m/s.
Usando duas vezes a conservação da energia mecânica:
AB
CD

EMec
 EMec
2
m v CD
m v 2AB
 mgh 
2
2

v2
42
 10(2, 4)  CD
2
2
2
 v CD
 64  vCD = 8
ms.
CD
EMec
 EEMec 
2
m v CD
 mgH 
2
Resposta
da
82
 10 H  H = 3,2 m.
2
questão
46:
a) Dados: P = 8 MW = 8  106 W; m = 500 t = 5 105 kg; v0 = 0; v = 288 km/h = 80 m/s.
O trabalho realizado pela força impulsora dos motores pode ser calculado pelo
teorema da energia cinética.
Página 108 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
WFv
motor
 Ecin 
m v2 m v02 5  105  802


 16  108 J.
2
2
2
Mas:
P
WFv
motor
t

t 
WFv
motor
P

16  108
 t = 200 s.
8  106
b) Dados: m = 500 t = 5  105 kg; v0 = 0; v = 288 km/h = 80 m/s; r = 5 km = 5  103 m;
N = 80 rodas.
Se a velocidade é constante, a força resultante na direção horizontal é
estritamente radial. Ou seja, essa força é a resultante centrípeta. A força atuante em cada
roda é:
Froda
R
 Cent 
N
m v2
2
5
2
r  m v  5  10  80 
N
Nr
80  5  103
Froda = 8.000 N.
c) Dados: m = 500 t = 5  106 kg; v0 = 0; v = 288 km/h = 80 m/s; P = 8  106 W.
Nesse item há um deslize da banca examinadora, pois não foi especificado se a
frenagem ocorre em um trecho retilíneo ou curvilíneo.
Suponhamos que seja em um trecho retilíneo. Sendo a o módulo dessa
aceleração, da expressão da potência instantânea, vem:
P = Fv  P = mav  a 
Resposta
P
8  106

 a = 0,2 m/s2.
5
m v 5  10  80
da
questão
47:
a) Dados: h = 5 m; v0 = 0; g = 10 m/s2.
Pela conservação da energia mecânica:
final
inicial
EMec
 EMec

m v2
 mgh
2

v  2 g h  2 10 5  
v = 10 m/s.
b) Dados: m = 20 kg; g = 10 m/s2.
Página 109 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Pelo princípio da ação-reação, a força média Fm  que a tábua aplica no saco tem
v
a mesma intensidade da força que o saco aplica na tábua.
Pelo princípio da inércia, como da tábua não sofre aceleração, a intensidade (Fm)
da força que o saco aplica na tábua tem a mesma intensidade da força que o peito do
homem aplica na tábua. E, novamente, pelo princípio da ação-reação, a força que o
peito do homem aplica na tábua (através dos pregos) tem a mesma intensidade da força
média que a tábua aplica no peito do homem.
De acordo com o teorema do impulso: o impulso da força resultante  I Rv  é igual
v
à variação da quantidade de movimento  Q  .
v
v
v
| I Rv | =|Q |
Fm 

v
Fm  P t  m | v |

Fm 
v
m | v |
m g 
t
20 10 
 200  Fm = 4.200 N.
0,05
c) Dados: A = 4 mm2 = 0,04 cm2; N = 400 pregos.
A intensidade da força média aplicada por cada prego no peito do homem é:
F1 
Fm 4.200

N
400

F1  10,5 N.
Calculando a pressão exercida por cada prego:
p
Resposta
F1 10,5

 p = 262,5 N/cm2.
A 0,04
da
questão
48:
[B]
Dados: MG = 300 g; MM = 100 g; VG = 80 km/h; VM = 24 km/h.
Página 110 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Antes da caça, os módulos das quantidades de movimento do gavião e do melro são,
respectivamente:
QG = 300 (80) g.km/h e
QM = 100 (24) g. km/h.
Como ocorre conservação da quantidade de movimento no momento da caça, o vetor
velocidade u tem a mesma direção da quantidade de movimento do sistema gaviãomelro.
Da figura:
tg 
QG 300(80)
 tg  = 10.

QM 100(24)
Resposta
da
questão
49:
a) A figura abaixo mostra as três forças atuantes no pica-pau.
Sejam | MPv | e | MCv | os módulos dos momentos dessas forças.
No triângulo destacado na figura:
Página 111 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
 1
–2
bP  16    8 cm  bP = 8  10 m.
2
 
v
Lembrando que o módulo do momento de uma força F é dado pelo produto da
sen30 
bP
16


intensidade dessa força pelo seu braço (b  distância da linha de ação da força até o
polo), vem:
| MPv | = P bP = 1  8  10–2  8  10–2 Nm.
| MCv | = C bC = 0, pois a linha de ação dessa força passa pelo ponto O (bC = 0).
b) Em módulo: | MTv | = T bT.
Como o pica-pau está em equilíbrio de rotação, o momento resultante sobre ele é
nulo. Ou seja, o somatório dos momentos no sentido horário é igual ao somatório dos
momentos em sentido anti-horário. Como MCv é nulo:
| MTv | = | MPv |  T bT = | MPv |  T (16  10–2) = 8  10–2 
T = 0,5 N.
c) Como o pica-pau está em equilíbrio de translação, a resultante das forças atuantes
sobre ele é nula. Pela regra da poligonal:
cos30 
C
P

C  Pcos30  1 0,87   C = 0,87 N.
v
Obs: Podemos calcular aqui, também, a intensidade da força T :
sen30 
Resposta
T
P

T  P sen30  1 0,5   T = 0,5 N.
da
questão
50:
Dados:
A = 40  50 = 2.000 cm2 = 0,2 m2  área de captação.
V = 300 mL = 300 cm3  volume de água.
0 = 25 °C  temperatura inicial da água.
Página 112 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
 = 100 °C  temperatura de ebulição da água.
IS = 1 kW/m2  Intensidade solar local.
c = 4 J/gC  calor específico sensível da água.
Lev = 2.200 J/g  calor específico latente de evaporação da água.
d = 1 g/cm3  densidade da água.
a) IS 
P
A

P  IS A  1
kW
 0,2 m 2  0,2 kW  P  200 W.
m2
b) E = m c   E = 300 (4) (100 – 25)  E = 9  104 J.
c) A massa de água é:
m = d V = 1 (300) = 300 g.
Para evaporar 1/3 dessa massa de água, a quantidade de energia é:
Eev 
m
300
Lev 
 2.200  Eev = 22  104 J.
3
3
A quantidade de energia necessária até 1/3 da massa de água ser evaporada é:
Etotal = E + Eev = 9  22 104 = 31  104 J.
Calculando o tempo gasto até o momento considerado:
P
Resposta
Etotal
T

T
Etotal 31 104

 T = 1.550 s.
P
200
da
questão
51:
a) Dados: M = 430 kg; D = 2,4 m; d = 0,6 m; sen 30° = 0,5; cos 30° = 0,86; g = 10
m/s2.
Página 113 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Como o braço está em equilíbrio de rotação, o momento resultante é nulo.
Assim, em relação ao ponto O, temos:
MFy  MP  Fy d = M g D  F cos 30° (0,6) = 430 (10) (2,4)  F =
10.320
0,6  0,86 

F = 20.000 N.
b) Dado: F = 4,5 N.
Da figura dada, a superfície de contato com a madeira é um retângulo de 0,2 mm
por 30 mm. Então a área é:
A = 30 (0,2) = 6 mm2 = 6  10–6 m2.
Da definição de pressão:
p=
F
4,5
 p = 7,5  105 N/m2.

A 6  106
Resposta
da
questão
52:
[B]
De acordo com a lei de Snell, quando a luz passa do meio menos para o mais refringente
a luz aproxima-se da normal e, quando passa do mais para o menor refringente, a luz
afasta-se da normal.
Página 114 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
As figuras mostram as duas situações propostas na questão: n > 1,4 e n < 1,4.
Analisando-as, concluímos que para n > 1,4, o objeto comporta-se com lente
convergente.
Resposta
da
questão
53:
Dados: nar = 1; nágua = 1,3;
Na figura a seguir:
  ângulo de incidência.
(90° – )  ângulo de refração.
a) Da figura acima, no triângulo APC:
tg 
0,9
 0,9 .
1
Da tabela dada,  = 42°.
Página 115 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Aplicando a lei de Snell:
nágua sen  = nar sen (90° – )  (1,3) (0,67) = (1) sen (90° – )  sen (90° – ) =
0,87.
Recorrendo novamente à tabela dada:
90° –  = 60°   = 30°.
c) Da figura acima, no triângulo ABI:
tg 
y
y
 tg 30 
 y = 0,9 (0,58) 
x
0,9
y = 0,52 m.
Resposta
da
questão
54:
[B]
I. Correta.
II. Correta.
III. Incorreta. Num olho míope, a imagem de um objeto distante forma-se antes da
retina.
Resposta
da
questão
55:
[C]
Para maior clareza, destaquemos dois pontos, A e B, do gráfico:
Página 116 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
I. Incorreta. Quando a resistência é constante, tensão e corrente são diretamente
proporcionais, portanto o gráfico é uma reta que passa pela origem.
II. Incorreta. Calculemos a resistência para os pontos, A e B, destacados na figura:
RA 
UA
2

 13,3 .
iA
0,15
RB 
UB
6

 24 .
iB
0,25
Portanto, a resistência aumenta com o aumento da corrente.
III. Correta. Calculemos as potências dissipadas para os valores dos pontos destacados:
PA = UA iA = 2 (0,15) = 0,3 W.
PB = UB iB = 6 (0,25) = 1,5 W.
PB > PA  a potência dissipada no filamento aumenta com o aumento da tensão
aplicada.
Resposta
da
questão
56:
Obs: o examinador poderia ter sido mais ameno e facilitado um pouco a resolução,
dando a dica de que 1 m2 = 10–12 m2. Por isso, a questão foi considerada de dificuldade
elevada. Muitos candidatos podem não ter percebido o detalhe da transformação.
a) Dados: A = 2,8 m2 = 2,8  (10–6 m)2 = 2,8  10–12 m2; d = 1,4  10–10 m; T1 = 300 K;
T2 = 302 K.
Página 117 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Como o intervalo de temperatura em questão é pequeno, podemos considerar a
condutividade térmica constante. Do gráfico:
k = 4  103 W/(mK).
Substituindo esses valores na expressão dada:

4  103  2,8  1012  302  300 
kA  T2  T1 

1,4  1010
d

  1,6  102 W .
b) Dados:  = 1,0  10–8 m; L = 1,4 m = 1,4  10–6 m; A = 70 nm2 = 70  (10–9 m)2 =
70  10–18 m2; i = 40 A = 40  10–6 A.
Da 1ª lei de Ohm: U  R i 
L
1 108  1,4  106  40  106


LU i 
A
70  1018
Da 2ª lei de Ohm: R   
A
U = 8,0  10–3 V.
Resposta
da
questão
57:
a) A figura a seguir mostra a tabela dada e o gráfico pedido:
b) A expressão da potência elétrica é dada pelo produto da tensão pela corrente. Logo, a
potência é máxima quando esse produto é máximo.
Pm = U Imáx .
A tabela mostra esses produtos e destaca que a potência máxima é:
Pm = 0,45 W.
Página 118 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Como se trata de um resistor não ôhmico (resistência variável), devemos usar a
1ª lei de Ohm para o par tensão – corrente correspondente à potência máxima.
Da tabela:
U = RI R
U 0,5

 R  0,56 .
I 0,9
U (volt)
I (ampère)
P (watt)
0,10
1,0
0,10
0,20
1,0
0,20
0,30
1,0
0,30
0,40
0,98
0,39
0,50
0,90
0,45
0,52
0,80
0,41
0,54
0,75
0,41
0,56
0,62
0,35
0,58
0,40
0,23
0,60
0,00
0,60
c) Dados: ISolar = 1 kW/m2; 103 W/m2; A = 20 cm2 = 2  10–3 m2.
Para U = 0,3 V, da tabela do item anterior, a potência fornecida é: Pfornecida = 0,3
W.
Calculando a potência incidente:
Pincidente = ISolar A = 103  2  10–3  PIncidente = 2 W.
De acordo com a expressão fornecida no enunciado: Eficiência 
Pfornecida
.
Pincidente
Então:
Eficiência =
0,3
 Eficiência = 0,15 = 15%.
2
Página 119 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
58:
a) Dados: Ti = 300 K; Pf = Pi 3 ; Vf = 4 Vi.
Aplicando a equação geral dos gases ideais:
Pi Vi
Ti

Pf Vf
Tf
Pi Vi

300
Pi

4Vi
3
Tf

Tf 
4
300
3

Tf = 400 K.
Tinicial  300 K  Uinicial  12 mV
Tfinal  400 K  Ufinal  16 mV
Do gráfico dado: 
 U  Ufinal  Uinicial  16  12

U = 4 mV.
b) Dados: R1 = 0,3  , R2 = 0, 4  ; R3 = 1, 2  ; Q = 540 J; t = 40 s.
Calculando a resistência equivalente do circuito mostrado:
Req  R1 
R2  R3
0,4  1,2
 0,3 
 0,3  0,3
R2  R3
0,4  1,2

Req  0,6 .
A potência drenada é:
Pdren 
Q 540

t 40
 Pdren  13,5 W.
Mas a potência drenada é 10% da potência total dissipada:
Pdren = 0,1 PT  PT 
Pdren 13,5

0,1
0,1
 PT  135 W.
Usando a expressão da potência dissipada em um circuito:
PT  Req ic2  ic 
PT
135

 225 
Req
0,6
Ic = 15 A.
Resposta
da
questão
59:
a) Dados: 0 = 1,3  10–6 T.m/A; N = 25.000 espiras; L = 0,65 m; i = 80 A.
N
L
B = 0 n i  B = 0 i = 1,3  106 
25.000
 80 
0,65
B = 4,0 T.
Página 120 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Dados: m = 200 g = 0,2 kg; d = 2 mm = 2  10–3 m; aR = 0,5 m/s2; g = 10 m/s2.
Se o imã sobe em movimento acelerado, Fm > P.
Do Princípio Fundamental da Dinâmica:
Fm – P = m aR  Fm = m aR + m g = 0,2 (0,5 + 10)  Fm = 2,1 N.
Calculando o trabalho:
WFv  Fm d  2,1 2  103  WFv  4,2  103 J.
m
m
Resposta
da
questão
60:
[C]
Do gráfico, concluímos que o tempo entre dois picos consecutivos (período) é T = 10–16
s.
Como:
f=
1
1
16
 16  f = 10 Hz, o que corresponde à radiação ultravioleta.
T 10
Resposta
da
questão
61:
a) Dados: λ verde = 500 nm; λ vermelho = 650 nm.
Da equação fundamental da ondulatória:
c     

. (I)
c
Da equação de Planck:
E  h. (II)
Combinando (I) e (II):
E
hc
.

Fazendo a razão pedida.
Página 121 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
hc
Everde
verde

650
R

 vermelho 
c
Evermelho h
 verde
500
vermelho

R  1,3.
b) Dados: h  6,6  1034 J  s ; m = 5  1026 kg ; λ  660 nm = 6,6 107m .
A variação da quantidade de movimento do átomo é igual à quantidade de
movimento do fóton:
v
v
v
h
6,6  1034
h
pátomo = pfóton  m v átomo =

 0,02 
 v átomo 
 m 6,6  107  5  1026

v
átomo
 2  102 m / s .
Resposta
da
questão
62:
a) Dados: n = 1,3; c  3  108 m / s .
A velocidade máxima das partículas deve ser igual à velocidade da luz na água.
Da expressão do índice de refração:
n
c
vmáx
 vmáx 
c 3  108

 vmáx  2,3  108 m / s .
n
1,3
b) Dados: d = 1,6 m; t = 12 ns  12  109 s ; cos 50° = 0,64.
A radiação emitida pela partícula tem a velocidade da luz no meio (v ).
vl 
d
1,6

t 12  109

v l  1,33  108 m/s.
Da figura dada:
cos50 
Resposta
vl
vp
 vp 
1,33  108
 vp  2,1 108 m / s .
0,64
da
questão
63:
[B]
Dados: h = 2.000 m; g = 10 m/s2;  = 0,9 g/cm3 = 9 102 kg/m3.
Página 122 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Do teorema de Stevin:
P =  g h = 9 102  10  2  103 = 180  105  P = 1,8  107 Pa.
Resposta
da
questão
64:
[D]
Dados: g = 10 m/s2-; e = 0,60; c = 0,80; m = 1;200 kg.
A força que a pista exerce no veículo tem duas componentes: normal e de atrito.
Supondo que a frenagem ocorra em pista horizontal, a componente normal (N) da força
que a pista aplica no veículo tem intensidade igual à do seu peso (P) .
N = P = m g = 12.000 N.
A componente de atrito estático máxima: Fat máx = e N = 0,8 (12.000)  Fat Max = 9.600
N.
A componente de atrito cinético: Fat cin = c N = 0,6 (12.000)  Fat cin = 7.200 N.
Resposta
da
questão
65:
[A]
Conforme sugere a figura, à medida que as bolhas sobem, elas sofrem expansão, pois
reduz-se a pressão sobre elas.
Resposta
da
questão
66:
[D]
Dados: m = 5 g; c = 0,8 J/g·°C;  = [880 – (-20)] = 900 °C.
Da equação fundamental da calorimetria:
Q = m c  = (5) (0,8) (900)  Q = 3.600 J.
Resposta
da
questão
67:
Página 123 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
[A]
Dados: E = 3  106 V/m; V = 9 kV = 9  103 V.
Como esse campo elétrico pode ser considerado uniforme, podemos escrever:
Ed = V  d 
V 9  103

= 3  10–3 m  d = 3 mm.
E 3  106
Resposta
da
questão
68:
[C]
Dados: A = 5,0  10–4 m2; d = 2 mm = 2  10–3; 0  9  10–12
C
; Q = 4,5  10–9 C.
V m
Combinando as expressões dadas:
A

(I)
Qd
C  ε0
 A
 (I) em II  Q   ε0  V  V 
.
d

ε0 A
 d
Q  C V (II)

Substituindo valores:
V
4,5  109  2  103
 V = 2,0  103 V.
12
4
9  10  5  10
Resposta
da
questão
69:
[B]
Seja x a distância percorrida pelo carro ao longo da pista, deste o instante da detecção
até o radar. Aplicando Pitágoras no triângulo mostrado na figura:
x2 + 502 = 1302  x2 = 14.400  x = 120 m.
Nesse mesmo triângulo:
cos  =
120 12
.

130 13
Página 124 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
72  13
12
Mas: Vm = Vr (cos )  72 = Vr    Vr =
 Vr = 78 km/h.
 13 
Resposta
da
12
questão
70:
[A]
Dados: f0 = 2,4  1010 Hz; v = 72 km/h = 20 m/s; c = 3  108 m/s.
Analisando a expressão dada: ∆f = f – f0 = ±
Vm
f0. Como o carro se aproximava, de
c
acordo com o enunciado, a frequência refletida é maior que a emitida (f > f0).
Assim a diferença ∆f = f – f0 deve ser positiva, ou seja, devemos escolher o sinal (+).
Então:
∆f = 
Vm
20
 2, 4  1010  f = 1.600 Hz.
f0  ∆f =
8
c
3  10
Resposta
da
questão
71:
[D]
Enquanto o avião voa horizontalmente, a bola permanece em repouso sobre a poltrona,
recebendo dela uma força normal de intensidade igual ao seu peso (N = P).
Se o avião apenas caísse em queda livre, com a = g, a bola permaneceria sobre a
poltrona, porém a normal se anularia (N = 0  estado de imponderabilidade).
No caso, a > g. Como a bola só está sujeita ao próprio peso, ela cai com abola = g, não
acompanhando a poltrona. Ou seja, em relação à poltrona, é como se a bola fosse
lançada para cima, com ay = a – g. Aliás, essa é mais uma função do cinto de segurança:
impedir que os corpos flutuem ou mesmo que “sejam lançados” contra o teto do avião.
Resposta
da
questão
72:
Dados:
Comprimento de cada volta: L = 27 km; c = 3  105 km/s; n = 11  103 voltas; t = 1 s.
a) v 
S n L 11.000 (27)



t
t
1
Página 125 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
v = 2,97  105 km/s.
b) A razão percentual dessa velocidade em relação à velocidade da luz é:
rP =
v
2,97  105
 100 
 100 
c
3  105
rP = 99%.
c) Sabemos da corrida em busca de novas armas envolvendo tecnologias nucleares.
Portanto, um primeiro interesse das nações envolvidas é bélico. Além disso, a
descoberta de novas tecnologias também pode ser aproveitada no desenvolvimento de
novos produtos, ou mesmo na redução dos custos de produção, melhorando o poder
aquisitivo e a qualidade de vida das pessoas. Há ainda um outro interesse que é a busca
por novas fontes para produção de energia.
Resposta
da
questão
73:
[E]
I. Errada. É desnecessário efetuar cálculos, pois 1 ano-luz é a distância que a luz
percorre em 1 ano, no vácuo. Em todo caso, iremos usá-los nos itens seguintes: d = v t
 d = (3105 km/s) (2,5106 anos3107 s/ano)  2,251019 km.
II. Correta. Veja os cálculos efetuados no item anterior.
III. Correta.
Resposta
da
questão
74:
a) A Fig 1 ilustra o terceiro encontro. Analisando-a, concluímos que até esse encontro
os espaços percorridos pelos dois corredores são:
SA = 300 – 20 = 280 m e SB = 300 + 20 = 320 m. Assim:
Página 126 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
VA 
SA 280

 VA  3,5 m/s;
t3
80
VB 
SB 320

 VB  4,0 m/s.
t3
80
b) A Fig 2 ilustra a distância percorrida entre o segundo e o terceiro encontros. Como as
velocidades são constantes, o intervalo de tempo entre esses encontros é metade do
intervalo entre o primeiro e o terceiro. ou seja: t2 = 40 s.
Então: dA = VA t2 = 3,5 (40)  dA = 140 m.
c) Em 8 voltas: DB = 8 (300) = 2.400 m.
O tempo gasto nesse percurso é:
t 
DB 2.400

 t  600 s.
VB
4
Nesse intervalo de tempo o corredor A percorre:
DA = VA t = 3,5 (600) = 2.100 m
A quantidade de voltas dadas por ele é:
NA =
DA
2.100
=
 7.
L
300
Resposta
da
questão
Dados: Largura do rio: D = 60 m; t = 2 min = 120 s; cos  =
75:
4
3
e sen  = .
5
5
A figura abaixo ilustra as velocidades, sendo: v a velocidade de Pedro em relação à
margem; v P a velocidade de Pedro em relação à água e vag a velocidade da água.
ag
a) v P 
ag
D
60


t 120
v P = 0,5 m/s.
ag
Página 127 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Da figura:
cos  
vP
ag
v

3 0,5
2,5

v

5
v
3
v = 0,83 m/s.
c) Da mesma figura:
sen 
vag
v

vag
4
10
10

 5vag 
 vag 

5 2,5
3
15
3
Vag = 0,67 m/s.
Resposta
da
questão
76:
a) Como A e Z se deslocam em sentidos opostos, o módulo da aceleração relativa entre
eles é a = 6 m/s2. A distância entre eles é D = 12 m.
Tratando-se de movimento uniformemente variado:
D=
1 2
1 2
2
a t  12 = 6 t  t = 4 
2
2
t = 2 s.
Poderíamos, ainda, considerar que, como as acelerações têm mesmo módulo, cada
jogador percorre até o encontro metade da distância que os separa, ou seja, d = 6 m.
d=
1 2
1 2
2
at  6 = 3t  t = 4 
2
2
t = 2 s.
b) Cada jogador tem velocidade constante de 6 m/s, em sentidos opostos. No intervalo
de 0,1 s, o deslocamento de cada um é
S = v t = 6 (0,1) = 0,6 m.
Portanto, no momento do lançamento, a distância mínima (Dmín) entre eles tem que ser:
Dmín = 2 (0,6) 
Dmin 1,2 m.
Página 128 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Poderíamos também usar a velocidade relativa entre eles: vrel = 12 m/s. Assim:
Dmín = vrel t = 12 (0,1)  Dmín = 1,2 m.
Resposta
da
questão
77:
[A]
A situação proposta sugere que consideremos, no início, movimento acelerado a partir
da origem (x0 = 0), com velocidade inicial não nula (v0  0) e, a seguir, movimento
uniforme. Por isso, os gráficos [I] e [II] são os que melhor representam as variações
espaço  tempo e velocidade  tempo, respectivamente.
Resposta
da
questão
78:
[B]
Seja L a distância horizontal entre a mancha e o dublê no instante do salto.
O tempo de queda do dublê é dado por: h =
A velocidade ideal (vi) é: vi =
1 2
2h
2(5)
gt  t 

 t  1 s.
2
g
10
L3 L3

 vi  L  3 ;
t
1
L
t
a velocidade mínima (vmin) é: vmin   vmin  L
e a velocidade máxima (vmax) é: vmax 
L6
 vmax  L  6.
t
Diferenças: Dmin = vi – vmin = (L + 3) – L  Dmin = 3 m/s;
Dmax = vmax – vi = (L + 6) – (L + 3)  Dmax = 3 m/s.
Página 129 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
79:
questão
80:
a) A2 = 0,8A1 = 1,6x 10-8 m2
F2 = P2A2 = (2,0x108 N/m2) x (1,6 x 10-8 m2) = 3,2 N
b) N 
VescM t
h
Resposta

0,6 m /s x10s
4
3x0,5m
da
Dados: g = 10 m/s2; tg 14° = 0,25.
a) As forças que agem na massa pendular são o peso e a tração.
b)
Como o movimento é retilíneo, a componente vertical da resultante é nula: Ty = P.
A resultante é então na direção horizontal: R = Tx. Como o vagão parte do repouso, ele
acelera no sentido da resultante, ou seja, para a direita.
Do princípio fundamental da dinâmica:
Página 130 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
R = m a  Tx = m amax. Como, na vertical, a componente da resultante é nula: Ty = P =
m g.
tg 14 
a
Tx m amax

 0,25  max  amax = 10 (0,25) 
Ty
mg
10
amax = 2,5 m/s2.
Resposta
da
questão
81:
a) Dados: S = 1,5 km = 1,5  103 m; EC = 4,5  104 J.
Como o trabalho da força peso é desprezível, a força de atrito (Fat) é a própria força
resultante.
Aplicando o teorema da energia cinética, considerando que, se a partícula é totalmente
freada, sua energia cinética final é nula:
R = EC 
4,5  10 4
1,5  103
| Fat | = |EC|

Fat S = |EC|
Fat =
| EC | | 0  4,5  10 4 |

=
S
1,5  103
questão
82:


Fat = 30 N.
b) Dados: m = 0,1 g;  = 2.400 °C; c = 0,90
J
.
g.C
Q = m c   0,1 (0,9) (2.400)  Q = 216 J.
Resposta
da
a) Dados: x = 6,4 nm = 6,4  10–9 m; d = 100 nm = 100  10–9 m = 10–7 m; b = 9,6 
10–39
N.m4;
x = 6,4 nm = 6,4  10–9 m.
Como sugere o enunciado:
FC = Felástica 
b
b
 k x  k = 4
4
d x
d
 k=

9,6  1039
107

4
 6,4  109

9,6  1039
6,4  1037

k = 0,015 N/m.
Página 131 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
b) Dados: ET = kB T; kB = 1,4  10–23 J/K; T = 300 K; kB = 0,21 N/m = 2,1 10–1 N/m.
(Houve aqui um deslize do examinador, atribuindo a kB duas constantes diferentes: a
primeira é constante de Boltzmann; a segunda é a constante elástica (k) da mola).
Como sugere o enunciado:
Eelástica
2
=

ET
kBT
2  1,4  1023  300
8,4  1021


 4  1020
k
2,1 101
2,1 101
k x2
 kB T 
2
x
=
 x = 2  10–10 m  x = 2
 10–1 nm  x = 0,2 nm.
Resposta
da
questão
83:
a) dados: T = 27 dias = (27  24) h; r = 3,8  108 m = 3,8  105 km.
v=
S 2  r
=
. Considerando  = 3, vem:
T
t
v=
2  3  3,8  105 1,9  105


27  24
54
v  3.520 km/h  978 m/s.
b) Dados: m = 70 kg; v = 2gRT ; RT = 6,4  106 m.
De acordo com o enunciado, a energia deve ser igual à energia cinética de lançamento:
E = EC =
1
1
mv 2 = m
2
2

2 g RT

2
1
2
= m 2 g RT = m g RT = 70 (10) (6,4  106) 
E = 4,48  109 J.
Resposta
da
questão
84:
[A]
Trata-se de um sistema mecanicamente isolado, pois apenas forças internas provocam
variações de velocidades. Assim, ocorre conservação da quantidade de movimento do
sistema. Como se trata de uma grandeza vetorial, as partículas + e – devem ter
velocidades de sentidos e de mesmo módulo, uma vez que as massas são iguais.
Página 132 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
85:
a) Dados: ma = 60 kg; mp = 80 kg; va = 0,15 m/s
Como se trata de um sistema isolado, há conservação do momento linear (quantidade de
movimento) do sistema (Q).
final
 Qa + Qp = 0  ma va + mp vp = 0  va = 
Qinicial
 Qsist
sist
mp vp
ma

80(0,15)
= – 0,2
60
m/s 
|va| = 0,2 m/s.
b) Após o empurrão, o momento linear do painel é:
Qp = mp vp = 80 (0,15) = 12 kg.m/s.
Como a força aplicada pelo astronauta é a responsável pela variação da velocidade do
painel, temos, pelo teorema do impulso:
I IFa | = QP = 12 N.s.
Conforme o próprio enunciado afirma, o módulo do impulso é numericamente igual a
área do gráfico.
I IFa | = Área  12 =
0,9  0,3
Fmax 
2
12 = 0,6 Fmax  Fmax =
12

0,6
Fmax = 20 N.
Página 133 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
86:
a) Dados: P0 = 100 kPa = 105 Pa; P = 0,94  105 Pa; h = 700 m, g = 10 m/s2.
A diferença de pressão ocorre devido peso da coluna de ar, de altura h = 700 m que,
conforme o teorema de Stevin, é dada por:
|P| = d g h 
d=
| P | 105  0,94  105 6  103
=


gh
10  7  102
7  103
d = 0,86 kg/m3.
b) Dados: R = 8,3
J
; H = 10 km.
mol.K
Da leitura direta dos gráficos, obtemos para altura de 10 km: pressão, P = 30 kPa = 3 
104
Pa;
temperatura,
T = –50 °C = (– 50 + 273) = 223 K.
Aplicando a equação de Clapeyron:
PV= nRT  V =
nR T
1 (8,3) (223)
 V=

P
3  104
V = 6,17  10–2 m3  V = 61,7 L.
Resposta
a)
da
Dados:
dar
questão
=
3
1,2
kg/m ;
dar 
M1
 M1  dar V  1,2 (1.500)  M1 = 1.800 kg.
V
b)
Dados:
T1
=
27
°C
=
300
K
e
V
T2
87:
=
=
m 3.
1.500
127°C
=
400
K.
Sendo M a massa molar do ar, aplicando a equação de Clapeyron, vem:
Patm V 
M1
RT1 (equação
M
I)
Patm V 
M2
RT2 (equação
M
II)
Dividindo
1=
(I)
por
(II),
obtemos:
M1T1
M T 1.800 (300)
 M2 = 1.350 kg.
 M1T1  M2T2  M2  1 1 
M2T2
T2
400
Página 134 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
c) Dados: massa total: m = mpassag + M2 = 400 + 1.350 = 1.750 kg; dar = 1,2 kg/m3.
As
forças
Aplicando
que
agem
no
o
princípio
balão
são
o
fundamental
peso
da
e
o
empuxo.
dinâmica,
temos:
E – P = m a  dar g V – m g = m a  (1,2) (10) (1.500) – 1.750 (10) = 1.750 a  18.000
–
a
17.500
=
1.750
a

500
 a = 0,29 m/s2.
1.750
Resposta
da
questão
88:
[B]
Q = m c T  m =
Q
3,6  107

 m  120 kg.
cT 1,2  103 (550  300)
Resposta
da
questão
89:
[D]
As lâmpadas L1 e L3 são consideradas fontes puntiformes, iluminando regiões de
mesma forma, semelhantes ao triângulo da máscara e de mesma orientação, conforme
ilustrado nas figuras abaixo.
Página 135 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
A Lâmpada L2 comporta-se como uma fonte extensa na direção vertical. A fig.1 (a
seguir) mostra as regiões iluminadas se somente a extremidades do filamento (duas
fontes puntiformes, Fa e Fb) estivessem acesas.
A fig.2 mostra o filamento como se várias fontes puntiformes fossem intercaladas entre
Fa e Fb.
Como uma fonte extensa é, na verdade, um conjunto de infinitas fontes puntiformes,
cada uma delas forma um triângulo iluminado. A região iluminada por L2 é a
superposição desses infinitos triângulos, como mostrado na fig.3.
Resposta
da
questão
90:
a) Para um material convencional, o raio incidente e o raio refletido estão no mesmo
meio, em quadrantes adjacentes (raio B); o raio incidente e o refratado estão em meios
diferentes, em quadrantes opostos (raio D).
Página 136 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Assim, para um metamaterial, a trajetória é a do raio E.
Dados: 1 = 60°; 2 = 45°; n1 = 1,8.
|n1| sen 1 = |n2| sen 2
 2
 1
1,8    n2 
 
2
 2 
1,8
n2 
1,4
|n2|  1,29.
b) Dados:  = 2,0  10–11
2
C2
–6 N.s
e

=
1,25

10
C2
N.m2
Substituindo valores na expressão dada:
v
1
 v=
εμ
Como n =
n=
3  108
2  108
1
2  10
11
 1,25  10
6

1
25  10
18

1
9
5  10
 v = 2,0  108 m/s.
c
, vem:
v
 n = 1,5.
Resposta
da
questão
91:
a) Dados: nvi = 1,532.
Analisemos a Fig 1 que mostra a refração sofrida pelo raio violeta.
Página 137 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Aplicando a lei de Snell:
nvi sen 30° = nar sen vi  1,532 (0,5) = 1 (vi)  vi = 0,766.
Consultando a tabela dada, encontramos: vi = 50°.
Na Fig 2:
 + 30° = 50°   = 20°.
b)
c) Sabemos que na refração, o desvio angular cresce do vermelho para o violeta.
Comprovemos aplicando a lei de Snell para as demais radiações envolvidas.
O ângulo de incidência é 1 = 30° para todas as radiações. Assim:
nrad sen 30° = nar sen 2  sen 2 = nrad (0,5). Então:
sen az = 1,528 (0,5) = 0,764;
sen vd = 1,519 (0,5) = 0,760;
sen am = 1,515 (0,5) = 0,758.
No intervalo de 0° a 90°, quanto menor o seno do ângulo, menor é o ângulo. Portanto, o
raio amarelo é o que sofre menor desvio, depois, nessa ordem, verde, azul e violeta.
Vejamos no esquema.
Página 138 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Resposta
da
questão
92:
a) Dado:  = 3.
Vejamos as medidas assinaladas na figura a seguir.
Nessa figura, obtemos para o diâmetro do ponteiro dos segundos: D = 58,0 mm.
O período desse ponteiro é: T = 60 s.
A cada volta, o espaço percorrido pela extremidade desse ponteiro é: S =  D.
v=
174
S  D 3 (58)
 v=



60
t
T
60
Página 139 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
v = 2,9 mm/s.
Uma segunda solução é considerarmos que, entre as marcas de 14 s e 16 s, a trajetória
da extremidade do ponteiro é praticamente retilínea, aproximadamente, igual a 6,0 mm,
como destacado na figura.
S 6,0
 v = 3,0 mm/s.

t
2
v=
b) Dados: q = 2,4 A.h = 8,64  103 C; t = 400 dias = (400  24) h.
A corrente elétrica média é dada por:
i=
q
2,4
0,1


 2,5  104 A 
t 400  24 400
i = 0,25 mA.
Resposta
da
questão
93:
[C]
A carga transferida no raio é: Q = i t = 300.000(0,5) = 150.000 C.
A fração pedida é:
Q
150.000 1

 .
| QTerra | 600.000 4
Resposta
da
questão
94:
a) Dado: A = 0,25 cm2 = 0,25  10–4 m2.
A intensidade da força exercida pelo dedo é, baseada na experiência do cotidiano,
equivalente ao peso de um corpo de massa 100 g = 0,1 kg. Assim:
F = P = m g = 0,1(10) = 1 N.
A pressão é:
p=
F
1

 p = 4  104 N/m2.
A 0,25  104
b) Dados: R = 2 k; U = 6 V.
Página 140 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Fechando a chave A, o percurso da corrente elétrica é o indicado na figura a seguir.
A resistência equivalente é:
Req =
3 R 3 (2)
R
 Req = 3 k = 3  103 .
R 

2
2
3
A corrente no circuito é, então:
U = Req I  I 
U
6
 I = 2  10–3 A..

Req 3  103
A corrente I divide-se igualmente para os dois ramos em paralelo, uma vez que eles têm
resistências iguais. Assim:
i=
I 2  103
=
 i = 1  10–3 A
2
2
Calculando a diferença de potencial entre os pontos C e D:
UCD = R i = (2  103)  (1  10–3) 
UCD = 2 V.
Resposta
da
questão
95:
a) A resistência equivalente de dois resistores em série é: RS = R1 + R2.
Para os mesmo dois resistores em paralelo é: RP =
R1 R2
R1  R2
.
Provemos que RS > RP:
RS = R1 + R2. Vamos multiplicar e dividir por R1 + R2. Então:
R12  2 R1 R2  R22
 R  R2 
RS  R1  R2  1

R

.

S
R1  R2
 R1  R2 
Como os denominadores são iguais, e todos os valores são positivos, basta
compararmos os numeradores.
Como R12  2 R1 R2  R22 > R1 R2  RS > RP. (C.Q.P.)
Página 141 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Da expressão da primeira lei de Ohm:
I=
U
, concluímos que a associação que apresenta maior corrente, é aquela que
R eq
tem menor resistência equivalente e vice-versa. Portanto, na caixa C os resistores estão
associados em série e, na caixa C’, em paralelo, conforme ilustram as figuras abaixo:
b) Novamente, da primeira lei de Ohm: Req 
U
. Então:
I
RS 
U
3
 R1  R2 
 R1  R2  50 (equação I)
I
0,06
RP 
R R
R R
U
3
 1 2 
 1 2  12 (equação II)
I'
R1  R2 0,25
R1  R2
Substituindo (I) em (II):
R1 R2
50
 12  R1 R2  600 (equação III)
Analisando as equações (I) e (III), por tentativas, fica fácil descobrir que os dois
números que somam 50 e têm produto 600 são 20 e 30.
Página 142 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Caso não dê “de cabeça”, podemos, na equação (III), fazer: R2 
600
(equação
R1
IV)
Substituindo (IV) em (I) vem:
R1 
600
 50 (M.M.C. = R1) 
R1
R12  600  50 R1  R12  50 R1  600  0.
Resolvendo essa equação do segundo grau, concluímos que R1 = 20 e R1' = 30.
Voltando em (IV):
R2 
600
600
= 30 e R'2 
= 20.
20
30
Finalmente, temos as possibilidades: R1 = 20  e R2 = 30  ou R1 = 30  e R2 =
20 .
Resposta
da
questão
96:
a)
De acordo com os pontos assinalados nos gráficos, a resposta é: 35 anos para homens e
45 anos para as mulheres.
b) a potência elétrica é dada por: Ps = Vsis e Vs=50Vc . Assim, is 
Resposta
da
questão
0,3mW
 0,6 mA
50x10mV
97:
a) Dados: E = 1,0  10–4 V/m; L = 2,0 cm = 2,0  10–2 m.
Sendo U a ddp indicada pelo voltímetro V, temos:
U = E L = 10–4  2  10–2  U = 2  10–6 V 
Página 143 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
U = 2 V.
b) No equilíbrio: FE = FB  qE  qvB  v 
E 1,0x104


B
0,2
v = 5  10–4 m/s.
Resposta
da
questão
98:
[E]
A aproximação do ímã provoca variação do fluxo magnético através do anel. De acordo
com a Lei de Lenz, sempre que há variação do fluxo magnético, surge no anel uma
corrente induzida. Essa corrente é num sentido tal que produz no anel uma polaridade
que tende a ANULAR a causa que lhe deu origem, no caso, o movimento do ímã. Como
está sendo aproximado o polo norte, surgirá na face do anel frontal ao ímã, também um
polo norte, gerando uma força de repulsão entre eles.
Resposta
da
questão
99:
a)
A figura mostra as forças que agem sobre
um íon: a força elétrica no mesmo sentido do campo elétrico, pois os íons são positivos;
pela regra da mão direita encontramos a força magnética, oposta à força elétrica. Para o
íons que passam pela fenda F2 essas forças se equilibram. Então:
Fmag  Felet  q v B1  q E 
v
E
.
B1
'
b) A força magnética (Fmag
) devida a B2 exerce o papel de resultante centrípeta. Então:
Página 144 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
'
Rcent = Fmag

m v2
m B2 R
.
 q v B2  
R
q
v

Substituindo o v pela expressão encontrada no item anterior  v 

E
 , vem:
B1 
m B2 R


q E
B1
B
m
1 B2

R.
q
E
c) Dado: B'2 = 2 B2.
Isolando R na expressão obtida no item
anterior, obtemos:
R
mE
.
q B1 B2
O novo raio, R’ é, então:
R' 
mE
mE
 R' 
.
q B1 2 B2
2 q B1 B2
A razão entre esses raios é:
q B1 B2
mE
R'
R' 1


  
R 2 q B1 B2
mE
R 2
R' 
Resposta
R
.
2
da
questão
100:
[C]
Analisando o gráfico, notamos que o período (T) é ligeiramente maior que 2,5 ms.
Página 145 de 146
LISTA DE EXERCÍCIOS 2 – FUVEST/UNICAMP – 3ª SÉRIE
Para o período de 2,5 ms, a frequência seria: f =
1
1

 400 Hz. Logo, a
T 2,5  103
frequência é ligeiramente menor que 400 Hz, ou seja, está sendo emitida a nota sol.
Página 146 de 146