UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Questões resolvidas -
Aula 05
Serão consideradas apenas as respostas indicadas com caneta no campo “Resp: ”, sendo obrigatória a
presença dos cálculos que as respaldem.
Nome: ____________________________________________________ Matrícula:____________________
Matrícula
11311252
11021538
11011920
LX
(µm )
10
11
12
R1
(Ω)
V2
(V)
V3
(V)
250
255
260
10
11
12
16,5
17,0
17,5
Matrícula
11318230
11228307
11517895
LX
(µm )
10
11
12
R1
(Ω)
V2
(V)
V3
(V)
270
275
280
10
11
12
25,5
26,0
26,5
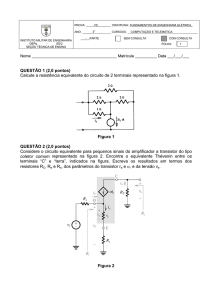
Considere o circuito ao lado (obtenha R1 de sua tabela), e suponha modelo de
diodo com queda de tensão constante (0,7 V).
(a) Determine o menor valor de RS que garante a condução de D2.
Resp:_____________
A condução de D2 força uma tensão máxima em R1 de 3,3 V. Determinemos o
valor de RS que faz com que a tensão em R1 seja 3,3 V SEM A CONDUÇÃO de D2,
ou seja, estaremos na FRONTEIRA DE CONDUÇÃO. Desta forma, ficamos com o
circuito abaixo:
Para que isso ocorra, temos que:
R1
R
⋅ 4,3 = 3,3 ⇒ RS = 1
R1 + RS
3,3
(se você quiser ser preciso, poderia dizer que RS precisa ser maior que o valor acima. Iremos continuar
adotando a fronteira, dando importância ao entendimento do funcionamento do circuito)
UFPB/CEAR/DEE — Dispositivos Eletrônicos
1/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
(b) Com base no valor de RS calculado no item anterior, qual a corrente no diodo D1? Resp:_________
Como haverá 1 V na resistência RS, a corrente no diodo D1 será dada por:
I D1 =
1
3,3
=
RS
R1
(c) Ainda com base no valor de RS calculado no item anterior, qual a corrente no diodo D2?
Resp:_________
Como se está na fronteira de condução, a corrente será nula (0+).
(d) Ainda com base no valor de RS calculado no item anterior, qual a corrente na resistência R1?
Resp:_________
O valor da corrente em R1 será o mesmo que em Rs, ou seja:
I R1 =
3,3
R1
Se, por exemplo, R1=250 Ω, RS=250/3,3=75,7575Ω. Veja o resultado abaixo:
Para certificarmos que estamos na fronteira de condução, veja o que acontece se variarmos a
resistência RS em 1 % para menos (75Ω) ou para mais (76,5151Ω):
UFPB/CEAR/DEE — Dispositivos Eletrônicos
2/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Exemplo de código Scilab para resolver o problema:
function calcula3 (R1);
// Calcule o valor da resistência série coloca D2 no limiar de condução
RS=R1/3.3;
mprintf ("RS que coloca D2 no limiar de condução = %.4e ohms\n", RS);
// Calcule e imprima o valor da corrente em D1
ID1=3.3/R1;
mprintf ("ID1 na condição anterior =%.2e A\n", ID1);
// imprima o valor da corrente em D2
mprintf ("ID2 na condição anterior =0 A\n");
// imprima o valor da corrente em RS
mprintf ("IRS na condição anterior =%.2e A\n", ID1);
endfunction
//Se você digitar :
calcula3 (250);
// vai aparecer:
RS que coloca D2 no limiar de condução = 7.5758e+01 ohms
ID1 na condição anterior =1.32e-02 A
ID2 na condição anterior =0 A
IRS na condição anterior =1.32e-02 A
UFPB/CEAR/DEE — Dispositivos Eletrônicos
3/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Matrícula
11011920
11311260
11211913
-3
ND(cm )
VX (V)
18
0,865
0,866
0,867
1,0 ·10
18
1,25 ·10
18
1,5 ·10
V1
(V)
2,50
2,55
2,60
V2
(V)
5,0
5,1
5,2
V3
(V)
16,5
17,0
17,5
Matrícula
ND(cm )
-3
VX (V)
11310017
11228606
11401368
5,0 ·10
18
5,25 ·10
18
5,5 ·10
18
0,881
0,882
0,883
V1
(V)
3,30
3,35
3,40
V2
(V)
6,6
6,7
6,8
V3
(V)
24,5
25,0
25,5
Considere o circuito abaixo. O capacitor C1 é um capacitor de grande valor, e sua função é isolar níveis
DC e acoplar sinais AC, ou seja, ele funciona como um circuito aberto para o cálculo da polarização, e
um curto-circuito para a análise AC. O circuito à direita do capacitor foi usado na caracterização
experimental da impedância (resistência) vista (pela esquerda) do ponto X, que na figura abaixo é
chamada de zvista. A técnica para medir indiretamente o valor (módulo) de zvista é relativamente
6
simples: basta calcular iteste= [(amplitude em Y) – (amplitude em X)]/10 (análise AC), e em seguida
dividir a amplitude em X por iteste, obtendo-se zvista. Como se conhece a amplitude de Y (conforme
figura abaixo, 10 V de amplitude), precisa-se apenas da amplitude de X. Esta medida não precisa de
nenhum parâmetro do diodo para ser executada! O seu objetivo nesta questão é prever a amplitude
do sinal AC em X, ou seja, você iria para o experimento SABENDO DA RESPOSTA!
-9
Considere: IS=10 A, η=1,9 (valores próximos do diodo 1N4148). Determine, com precisão, o valor da
resistência R1 para que a corrente de polarização do diodo seja 250 µA. Observe que o valor de V1
deve ser obtido da tabela. Em seguida, proceda à análise AC, e determine, com precisão, o valor da
amplitude em X. Resp. Amplitude em X=_______V (Dica: não confundir análise de polarização, em que
o capacitor funciona como um aberto, e análise AC, em que ele funciona como um curto-circuito e o
diodo deve ser subsituído por sua resistência dinâmica).
iteste
zvista
Começemos por calcular a tensão DC do diodo para que conduza uma corrente de 250 µA:
ID
250 ⋅ 10 −6
) = 0,6108128V
VD = η ⋅ VT ⋅ ln( ) = 1,9 ⋅ 0,0258649 ⋅ ln(
IS
⋅ 10 −9
Assim, a resistência R1 será dada por:
UFPB/CEAR/DEE — Dispositivos Eletrônicos
4/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
R1 =
V1 − VD
250 ⋅ 10 −6
Para a análise AC, a tensão V1 é anulada. A impedância Zteste será dada pelo equivalente paralelo de
R1 e a resistência dinâmica do diodo (rd). Calculemos primeiramente rd:
rd =
η ⋅ VT
250 ⋅10
−6
=
1,9 ⋅ 0,0258649
= 196,57Ω
250 ⋅10 − 6
A impedância Zteste será então:
zteste =
zteste ⋅ rd
zteste + rd
Finalmente, a amplitude em X será dada por:
X amplitude = 10 ⋅
zteste
zteste + 10 6
Exemplo de código Scilab para resolver o problema:
function calcula3 (v1);
is=1e-9;
eta=1.9;
vt=0.0258649;
id=250e-6;
// calcule do vd
vd=eta*vt*log(id/is);
// Calcule o r1
r1=(v1-vd)/id;
// imprima r1 na tela:
mprintf ("R1=%f ohms\n", r1)
// Calcule rd
rd= eta*vt/id;
// imprima rd na tela:
mprintf ("rd=%f ohms\n", rd)
// Calcule zteste
zteste= r1*rd/(r1+rd)
// imprima zteste na tela:
mprintf ("zteste=%f ohms\n", zteste);
// Calcule a amplitude em X
ampx= 10*zteste/(zteste+1e6);
// imprima a amplitude em X na tela:
mprintf ("Amplitude em X=%f volts\n", ampx);
endfunction
Se você digitar:
UFPB/CEAR/DEE — Dispositivos Eletrônicos
5/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
calcula3 (3.5);
Vai aparecer o seguinte:
R1=11556.748702 ohms
rd=196.573240 ohms
zteste=193.285570 ohms
Amplitude em X=0.001932 volts
Valor calculado=1,932 V. Valor PSPICE: 1,9324 V. Foi usado um capacitor C1 de 1 farad (não coloque 1
F, pois ele vai entender o F como femto).
UFPB/CEAR/DEE — Dispositivos Eletrônicos
6/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Matrícula
10921561
11128385
11324642
R1(Ω)
1k
1,1k
1,2k
VX (V)
0,726
0,727
0,728
VY (V)
Matrícula
1,5
1,51
1,52
10911567
11228321
11324637
R1(Ω)
2k
2,1k
2,2k
VX (V)
0,736
0,737
0,738
VY (V)
1,6
1,61
1,62
Considere o circuito ao lado. Supondo que o diodo apresenta IS=10-12 A, determine o
valor de η para que a tensão no ponto X indicado seja igual a 0,75 V. Resp: η=_________
VD
ID ≈ IS ⋅e
η ⋅VT
⇒ VD = η ⋅ VT ⋅ ln(
ID
) ⇒η =
IS
VD
VT ⋅ ln(
ID
)
IS
=
0,75
0,0258649 ⋅ ln(
Exemplo de código Scilab para resolver o problema:
function eta = calcula2 (r1);
// definição de is dado no problema
is=1e-12;
// definição de vt
vt=0.0258649;
// Calcule o eta
eta=0.75/(vt*log(2.25/(r1*is)));
// imprima o eta na tela:
mprintf ("eta=%e\n", eta)
endfunction
Se você digitar:
calcula2 (1000);
Vai aparecer o seguinte:
eta=1.346548e+00
UFPB/CEAR/DEE — Dispositivos Eletrônicos
7/20
3 − 0,75
)
R1 ⋅ I S
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Considere que uma resistência de 10 vezes o valor de R1 foi conectada
em paralelo com o diodo do circuito anterior. Observe que esta
resistência (10·R1) irá drenar uma pequena corrente em relação à
corrente do diodo no caso anterior, e portanto pode ser considerada uma
pequena perturbação no circuito (de modo que você pode usar uma
análise de pequenos sinais). Calcule o novo valor de tensão no ponto X.
Resp. VX=__________
Aqui você pode resolver por mais de uma forma. A primeira delas, que
requer uma calculadora científica, é determinando o equivalente thévenin do arranjo fonte-resistores:
VTH =
10 ⋅ R1
⋅ 3V = 2,727272V
10 ⋅ R1 + R1
RTH =
10 ⋅ R1 ⋅ R1
= 0,909090R1
10 ⋅ R1 + R1
Usando um processo iterativo, com os valores de IS e η do exemplo anterior, e com uma ajudinha do
scilab, teríamos (usaremos R1=1 kΩ, IS=10-12 A, η=1,346548):
function calcula3 (r1);
// definição de is dado no problema anterior
is=1e-12;
// definição de vt
UFPB/CEAR/DEE — Dispositivos Eletrônicos
8/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
vt=0.0258649;
// calcule eta usando o código anterior
eta = calcula2 (r1);
// calcule o equivalente thévenin:
vth=3*10/11;
rth=0.909090*r1
vd=0;
// chute inicial
// faça 4 iterações
for i=1:4,
id=(vth-vd)/rth
// valor de ID na n-ésima iteração
vd=eta*vt*log(id/is)
// valor de VD na n-ésima iteração
mprintf ("id%d=%e\n",i, id);
mprintf ("vd%d=%e\n",i, vd);
end
endfunction
Se você digitar:
calcula3 (1000);
Vai aparecer o seguinte:
eta=1.346548e+00
id1=3.000003e-03
vd1=7.600195e-01
id2=2.163981e-03
vd2=7.486424e-01
id3=2.176496e-03
vd3=7.488432e-01
id4=2.176275e-03
vd4=7.488397e-01
Então veja que o novo valor de VX é 0,74884, uma diferença de 1,16 mV em relação ao caso anterior.
Tentemos obter este valor por um outro método, que precisa apenas de aritmética básica.
Na questão anterior, VX=0,75. Com R1=1 kΩ, isso nos dá ID=2,25 mA. Com η=1,346548, a resistência
dinâmica do diodo é η·VT/ID =1,346548·0,0258649/0,00225 =15,48 Ω. O fato de colocar uma
resistência de 10· R1 em paralelo com o diodo da questão anterior (que tinha VX=0,75), faz com que
esta resistência adicionada “drene” uma corrente de aproximadamente 0,75/(10· R1)=75 µA (supondo
os valores que estamos adotando. Ora, esta corrente será “roubada” do diodo, e portanto a queda de
tensão no diodo será dada (na aproximação de pequenos sinais) por este valor de corrente
multiplicado pelo valor de resistência dinâmica do diodo. Assim: ∆VD=75 µA ·15,48 Ω= 1,16 mV!!!!
(com conta de papel e lápis!!!!), e a resposta é VX=0,74884 V.
UFPB/CEAR/DEE — Dispositivos Eletrônicos
9/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Considere o circuito ao lado. Assuma que o LED,
quando acende, apresenta em em seus terminais
uma tensão de 1,8V (é um LED vermelho).
Considere ainda que uma corrente de 1 mA é
necessária para a luz do LED ficar observável.
Determine o valor mínimo da tensão da fonte VIN
para que o LED acenda.
Resp: VINMIN=___________
Quando o LED está aceso, a tensão entre seus
terminais é de 1,8 V. Com uma corrente necessária de 1 mA, a tensão entre os terminais do resistor R1
é de 1mA · R1. Como o Zener está na ruptura, a tensão entre seus terminais é de 4,7 V. Assim:
VIN = 1,8 + 0,001⋅ R1 + 4,7
Exemplo de código Scilab para resolver o problema:
function calcula5 (r1);
vin=1.8+0.001*r1+4.7
mprintf ("Vin=%f\n",vin);
endfunction
Se você digitar:
UFPB/CEAR/DEE — Dispositivos Eletrônicos
10/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
calcula5 (1000);
Irá aparecer:
Vin=7.500000
Pra simular no PSPICE, você deve colocar um diodo para o qual VD=1,8 com ID= 1mA (escolha, por
-19
exemplo, η=2 e IS= 8·10 A), e no Zener, você deve definir “BV” (tensão de ruptura) e IBV (corrente na
tensão de ruptura). Se R1=1 kΩ, perceba que a corrente no zener será de 3,8 mA (por que?). Assim:
UFPB/CEAR/DEE — Dispositivos Eletrônicos
11/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Dispondo de diodos para os quais η=1 e VD=0,7V quando ID=1mA, projete um circuito que utiliza 4
destes diodos conectados em série, em série com um resistor R conectado a uma fonte de 10V. É
preciso que a tensão entre os terminais do conjunto de diodos seja de 3V (imagine que esta seja a
tensão de saída do seu circuito). Desenhe o seu circuito abaixo.
O circuito é mostrado ao lado. O (único) valor que você (ainda) precisa
determinar é o valor da resistência. No problema, são dados η e um ponto
da curva IxV: Com estes dados, determinanos Is:
VD
ID = IS ⋅ e
η ⋅VT
⇒ IS =
ID
VD
e
η ⋅VT
10 −3
=
e
0, 7
1⋅0 , 0258649
= 1,764 ⋅ 10 −15 A
Com este valor, obtemos o valor de corrente para o qual a tensão em cada
diodo será de 0,75V, de forma que o conjunto de 4 diodos tenha uma
tensão e 3V:
ID = IS ⋅ e
VD
η ⋅VT
= 1,764 ⋅ 10 −15 ⋅ e
0 , 75
1⋅0 , 0258649
= 6,911mA
Finalmente, para fazer passar 6,89mA nos diodos, o valor da resistência
será dado por:
R=
10V − 3V
= 1012,87Ω
6,911mA
UFPB/CEAR/DEE — Dispositivos Eletrônicos
12/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Considere o circuito ao lado. Considere ainda o modelo de
diodo com queda de tensão constante (VDON=0,7V).
Determine o valor de tensão da fonte A para que a
corrente I indicada seja 5mA.
Resp:
VA@I=5mA= 18,7 V
Raciocínio: Para que haja corrente I, o diodo zener no ramo central deve estar polarizado
diretamente (portanto, 0,7 V). Com uma corrente de 5mA passando pelo resistor vertical, sua
tensão é de 5 V. Desta forma, deve haver 5,7 V no nó central. Este valor faz com que o valor da
corrente no resistor da direita seja de (5,7-2-0,7)/1000=3 mA, que somados aos 5 mA do resistor
vertical, fazem com que a corrente no resistor da esquerda seja de 8 mA, e de forma que a tensão
em seus terminais seja de 8 V. Para que esta corrente atravesse o diodo zener do ramo da
esquerda, é preciso que ele esteja na ruptura (portanto, 5 V). Assim, a tensão no terminal esquerdo
do diodo zener do ramo esquerdo deve ser de 5,7+8+5=18,7 V.
UFPB/CEAR/DEE — Dispositivos Eletrônicos
13/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
No circuito abaixo, considere que o diodo tem os seguintes parâmetros: IS=10 A e η=1. Considere ainda que
VT=25,9mV. Observe que o circuito é estimulado por uma fonte de tensão DC de 10V em série com uma fonte de
tensão AC de 500mV de amplitude.
-16
(a)
Usando um processo iterativo, determine com
precisão a corrente no diodo, no caso em que a
tensão no ponto A é igual ao seu valor médio.
Resp: ID_VAMEDIO=0,9227mA. Neste caso, VA=10V.
Equações a resolver: ID=(10-VD)/10k; VD=ηVT*ln(ID/IS))
Iniciando com VD=0,7V => ID=(9,3)/10k=0,93mA; Assim
VD=1·0,0259*ln(0,93mA/10-16A)=0,7734V.
Iterando:ID=(10-0,7734)/10k=0,9227mA;
Assim
-16
VD=1·0,0259*ln(0,9227mA/10 A)=0,7732V. Finalmente:
ID=(10-0,7732)/10k=0,9227mA;
(b)
Usando um processo iterativo, determine com
precisão a corrente no diodo, no caso em que a tensão no ponto A é igual ao seu valor máximo.
Resp: ID_VAMAXIMO=0,9725mA.
Neste caso, VA=10,5V.Equações a resolver: ID=(10,5-VD)/10k;
VD=ηVT*ln(ID/IS)).
Iniciando
com
VD=0,7V
=>
ID=(10,5-0,7)/10k=0,98mA;
-16
VD=1·0,0259*ln(0,98mA/10 A)=0,7747V.
Iterando:ID=(10,5-0,7747)/10k=0,9725mA;
-16
VD=1·0,0259*ln(0,9725mA/10 A)=0,7745V. Finalmente: ID=(10,5-0,7745)/10k=0,9725mA
(c)
Assim
Assim
Usando um processo iterativo, determine com precisão a corrente no diodo, no caso em que a
tensão no ponto A é igual ao seu valor mínimo. Resp: ID_VAMINIMO=0,8728mA. Neste caso,
VA=9,5V.Equações a resolver: ID=(9,5-VD)/10k;
VD=ηVT*ln(ID/IS)). Iniciando com VD=0,7V =>
-16
ID=(9,5-0,7)/10k=0,88mA;
Assim
VD=1·0,0259*ln(0,88mA/10 A)=0,7719V.
Iterando:ID=(9,5-16
0,7719)/10k=0,8728mA; Assim VD=1·0,0259*ln(0,8728mA/10 A)=0,7717V. Finalmente: ID=(9,50,7717)/10k=0,8728mA.
(d) Derive a expressão da corrente do diodo em relação à tensão no diodo, encontrando a
condutância diferencial do diodo para o ponto de polarização (item (a)). Inverta o valor da
condutância diferencial para encontrar a resistência diferencial. Agora anule a fonte de tensão
DC e encontre a amplitude do sinal de tensão no diodo devido apenas à fonte AC, utilizando
para isso o modelo equivalente para pequenos sinais do diodo. Resp: VD-AC=1,39mV. O ponto de
polarização é ID=0,9227mA. Derivando a expressão da corrente em relação à tensão no diodo, obtemos
a expressão gd=ID/(ηVT)=0,9227mA/25,9mV=35,6mS. O inverso da condutância é a resistência dinâmica
do diodo, rd=(ηVT)/ID=1/0,0356=28Ω.Como a amplitude de tensão AC aplicada é de 0,5V, a tensão AC no
diodo terá amplitude de 0,5*28/10028=1,39mV. Observe que este valor é aproximadamente igual à
diferença entre o valor da tensão no diodo para VA=10V e 10,5V, ou para VA=10V e 9,5V.
UFPB/CEAR/DEE — Dispositivos Eletrônicos
14/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Considere os circuitos abaixo. Considere ainda o modelo de diodo com queda de tensão constante (VDON=0,7V).
(a) Determine o valor de tensão da fonte A no circuito da esquerda para que a corrente I indicada
seja 2mA. Resp: VA-2mA-esquerda=4,7V. A tensão no resistor vertical é 2mA·1kΩ=2V, de forma que
o circuito à direita deste resistor não conduz, podendo ser desconectado para análise.
(b) Determine o valor de tensão da fonte A no circuito da direita para que a corrente I indicada seja
5mA. Resp: VA-5mA-direita=23V. Para que haja corrente I, é preciso que o diodo zener esteja em
ruptura (5V). Com uma corrente de 5mA passando pelo resistor vertical, sua tensão é de 5V.
Desta forma, deve haver 10V no nó central. Este valor faz com que o valor da corrente no
resistor da direita seja de (10-2-0,7)/1000=7,3mA, que somados aos 5mA do resistor vertical,
fazem que a corrente no resistor da esquerda seja de 12,3mA, e de forma que a tensão em seus
terminais seja de 12,3V. Assim, a tensão no terminal esquerdo do resistor esquerdo deve ser de
10+12,3=22,3V, que somados aos 0,7 do diodo esquerdo totalizam 23V.
UFPB/CEAR/DEE — Dispositivos Eletrônicos
15/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Considere o circuito abaixo, que pode ser usado para carregar uma bateria de celular de 2,4V. O
circuito é alimentado por uma tensão nominal de 3V, tal como mostrado na figura.
(a) Determine o valor da corrente IX para que a saída seja de 2,4V para uma tensão de entrada de
3V. Resp: IX=__________A (IX=3-2,4/50=12mA)
(b) Com base no valor de IX calculado no item anterior, e sabendo que os diodos mostrados na
figura apresentam η=2, determine o valor de IS dos diodos para que a tensão Vout seja de 2,4V
sem carga (o celular está desconectado). Utilize VT=25,9mV. Resp. IS= _______A
(Is=IX/exp(0,8/(2*0,0258649))=2,306nA)
(c) Calcule o valor da resistência dinâmica dos diodos (rd) para variações de corrente em torno do
valor calculado no item (a). Lembre-se que os diodos apresentam η=2. Resp.: rd= ______Ω
(rd=η·VT/I=2*0,0258649V/12mA =4,3108Ω)
(d) Uma carga de 2kΩ é conectada à saída da fonte. Já que uma tal carga consome 1,2mA da fonte,
o que representa apenas 10% do valor da corrente nos diodos na ausência de carga, você pode
usar o modelo de pequenos sinais para simplificar a análise e encontrar a variação de Vout em
relação à condição sem carga (2,4V). Supondo que a corrente na carga é suprida por uma
diminuição da corrente nos diodos (ou seja, a corrente em R1 permanece praticamente
inalterada), qual o valor de Vout quando a carga é conectada? Resp.: _________V
(∆V=∆I·(3·rd)=1,2mA·3·4,3108Ω=15,5mV. Vout’=Vout-∆V=2.4-0,0155=2,384V)
UFPB/CEAR/DEE — Dispositivos Eletrônicos
16/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
No circuito abaixo, considere que os diodos D1 e D2 são idênticos, apresentam IS=10 A e η=1. Se IX=2mA,
determine a tensão em R1 com precisão. (dica1 : caso prefira, você pode transformar o circuito paralelo composto
pela fonte IX e pelo resistor R1 em um circuito série. Dica 2: para estes valores de IS e η, é provável que a tensão
em cada diodo permaneça entre 0,7V e 0,8V).
-16
Resp.: VR1=1,56V
(Pede-se a tensão no resistor R1, que é a mesma do circuito composto pelo arranjo série de dois diodos. Para
este último circuito (arranjo série de diodos), e apenas para ele, a fonte de corrente e o resistor de 2kΩ são
equivalentes a uma fonte de tensão de VDD=4V em série com uma resistência de RS=2kΩ.
Equações a resolver:
ID=(4-2VD)/2000;
VD=ηVT*ln(ID/IS))
-16
Iniciando com 2VD=1,4V => ID=(4-1,4)/2000=1,3mA; Assim VD=1·0,02586499*ln(1,3mA/10 A)=0,7810V.
-16
Iterando com 2VD=1,562V => ID=(4-1,562)/2000=1,2190mA; Assim VD=1·0,0258649*ln(1,21mA/10 A)=0,77935V.
A resposta é portanto muito próxima de 1,56V, que correponde a 2 vezes a tensão em cada diodo.
No circuito original, as equações a resolver são: ID=IX-IR1=0,002-(2VD/2000); VD=ηVT*ln(ID/IS))
Observe que 0,002 = 4/2000. Assim ID=IX-IR1=0,002-(2VD/2000)=(4-2VD)/2000, que é a mesma equação que a
anterior, e portanto o resultado é o mesmo (o que era de se esperar).
tensão direta de 0,7 V quando
conduzem (e tensão de ruptura infinita), e que os diodos Zener apresentam tensão de ruptura de 2,5V
(e tensão direta de 0,7 V). Indique o número de cada um dos diodos que está conduzindo. Uma resposta
Considere o circuito abaixo. Considere que os diodos comuns apresentam
errada anula uma resposta correta.
Resp.: Os diodos que estão conduzindo são os que têm esta numeração: ____________________________
(=3,4,5,6,9)
Os diodos 1 e 2 não conduzem por conta do diodo 2. Os diodos 7 e 8 não conduzem pois
precisariam de uma tensão de ao menos 2,5+0,7=3,2V pra conduzir (só há 3,0V), e o diodo 10 não conduz por
razões óbvias.
UFPB/CEAR/DEE — Dispositivos Eletrônicos
17/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
No circuito abaixo, os diodos D1 a D4 são iguais, têm η=1, e exibem uma queda de tensão de 0.7V quando estão
conduzindo uma corrente de 1mA.
Para pequenos valores do sinal de entrada vi (ex. 10mV de pico), encontre a relação vo/vi para os seguintes
casos:
(a) I = 1µA
R.=
(b) I = 100µA R.=
(c) I = 10mA
R.=
Trata-se de análise para pequenos sinais, ou seja, pequenas flutuações de tensões e correntes. Primeiramente, é
preciso notar que se a tensão vi for nula, a tensão vo também o será. Isso decorre do seguinte raciocínio:
Suponha inicialmente que vi=0 leva a vo=0, e portanto o sistema está equilibrado e cada diodo conduz I/2, já que
todos estão sob as mesmas tensões. Se vo pudesse se tornar maior que 0, a corrente em D4 é menor que a
corrente em D3 (já que parte da corrente em D3 vai para o resistor de 10kΩ). Mas isto é uma contradição, pois
supondo que as tensões em D1 e D2 não se alteraram em relação à condição de equilíbrio, um vo maior que zero
implica em uma corrente D4 maior que a corrente em D3. Você pode ainda imaginar cenários pitorescos de
combinações de tensões e correntes, mas todos os cenários levam a contradições (tente!).
Na condição de equilíbrio (vi=0, levando a vo=0), os 4 diodos conduzem I/2. Portanto, apresentam uma
resistência dinâmica para pequenos sinais de rd=η⋅Vt/ID =1⋅0,028649/I/2=0,0517298/I. Para análise de pequenos
sinais, as fontes de corrente (DC) são eliminadas (circuito aberto), enquanto que os diodos são substituídos por
suas resistências dinâmicas associadas. Veja o circuito abaixo:
rd
rd
vo
vi
UFPB/CEAR/DEE — Dispositivos Eletrônicos
18/20
rd
rd
10k
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
Para o cálculo da relação vo/vi, este circuito é equivalente ao circuito abaixo:
Para I=1µA,
rd=0,0517298/1e-6=51729kΩ
Para I=100µA, rd=0,0517298/1e-4=517,29Ω
Para I=10mA, rd=0,0517298/1e-2=5,1729Ω
=> vo/vi = 10k/61729k = 0,16199 V/V
=> vo/vi = 10000/10517,29 = 0,95081 V/V
=> vo/vi = 10000/10005,1729 = 0,99948 V/V
Para I = 1mA, qual é o maior valor de amplitude de tensão na saída (vo), para o qual a corrente nos diodos varia
por no máximo 10% do seu valor DC (I )? R.=
Qual é o valor de vi correspondente? R.=
Retomemos o circuito:
rd
rd
vo
vi
rd
rd
10k
Se I = 1mA, a corrente de polarização (DC) em cada diodo é de 0,5mA, e como a corrente que varia no tempo é
limitada a 10% deste valor, o limite da corrente pequeno sinal é de 50µA. Por sua vez, já que I = 1mA,
rd=0,0517298/1e-3=51.729Ω. Assim, a tensão pequeno sinal em cada diodo é de 51.729*0,05e-3=2,58649mV. O
valor de corrente pequeno sinal no resistor de 10kΩ é igual ao dobro do valor em cada diodo (veja o circuito
acima), de forma que é 100µA. Assim, vo=10000*100µA=1V. Já que a tensão pequeno sinal em cada diodo é de
2,58649 mV, vi=vo+2*2,58649mV=1,0051729V
Observe finalmente que quando vi é positivo, a corrente em D2 e D3 aumenta em relação a I/2, enquanto que a
corrente em D1 e D4 diminui. Quando vi é negativo, a situação é invertida.
SIMULE!!!!
UFPB/CEAR/DEE — Dispositivos Eletrônicos
19/20
UNIVERSIDADE FEDERAL DA PARAÍBA
CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
No circuito abaixo (à esquerda), considere que o diodo zener apresenta tensão de ruptura de 3V
(mecanismo zener), e use o modelo de queda de tensão constante (0,7V) para o caso de polarização
direta. Analise o circuito, e preencha a tabela abaixo (à direita).
VIN (V)
-5
-2
-1
0
1
2
5
Basta usar a lei das malhas.
SIMULE!!!!
UFPB/CEAR/DEE — Dispositivos Eletrônicos
20/20
VOUT (V)
-2,85 (diodo conduz diretamente, VD=0,7)
-1,35 (diodo conduz diretamente, VD=0,7)
-0,85 (diodo conduz diretamente, VD=0,7)
0 (diodo não conduz, VOUT=VIN)
1 (diodo não conduz, VOUT=VIN)
2 (diodo não conduz, VOUT=VIN)
4 (diodo conduz na ruptura, queda de
tensão de 3V reverso)