1) Em uma pista de competição, quatro carrinhos

LISTA EXTRA – 3ª SÉRIE
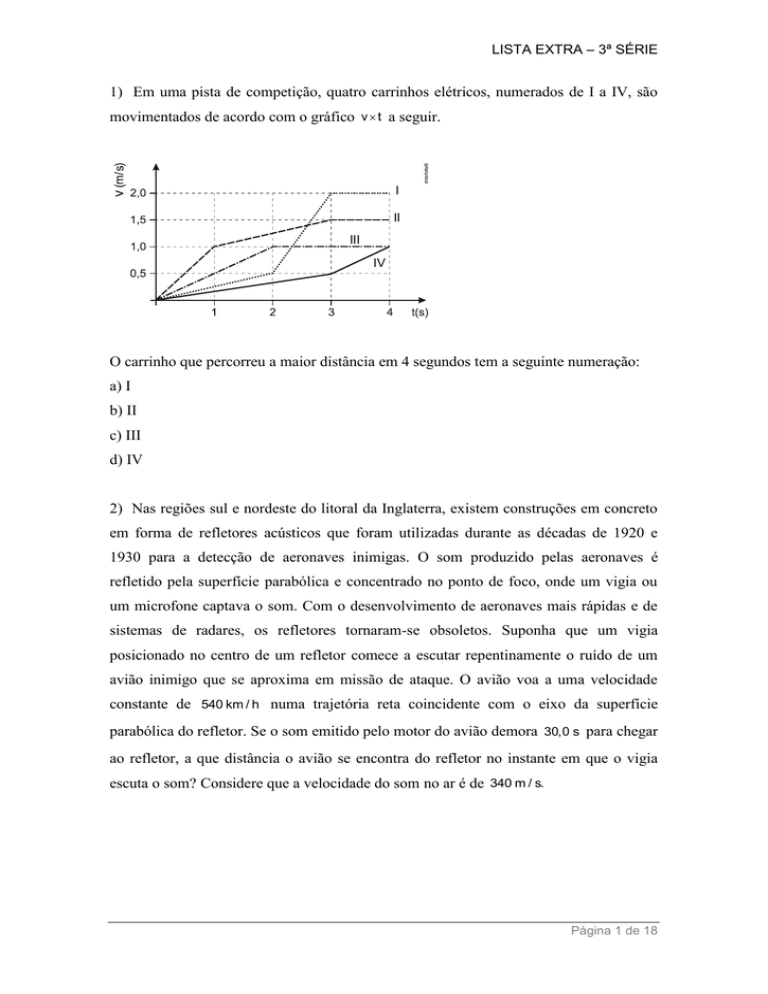
1) Em uma pista de competição, quatro carrinhos elétricos, numerados de I a IV, são
movimentados de acordo com o gráfico v  t a seguir.
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
2) Nas regiões sul e nordeste do litoral da Inglaterra, existem construções em concreto
em forma de refletores acústicos que foram utilizadas durante as décadas de 1920 e
1930 para a detecção de aeronaves inimigas. O som produzido pelas aeronaves é
refletido pela superfície parabólica e concentrado no ponto de foco, onde um vigia ou
um microfone captava o som. Com o desenvolvimento de aeronaves mais rápidas e de
sistemas de radares, os refletores tornaram-se obsoletos. Suponha que um vigia
posicionado no centro de um refletor comece a escutar repentinamente o ruído de um
avião inimigo que se aproxima em missão de ataque. O avião voa a uma velocidade
constante de 540 km / h numa trajetória reta coincidente com o eixo da superfície
parabólica do refletor. Se o som emitido pelo motor do avião demora 30,0 s para chegar
ao refletor, a que distância o avião se encontra do refletor no instante em que o vigia
escuta o som? Considere que a velocidade do som no ar é de 340 m / s.
Página 1 de 18
LISTA EXTRA – 3ª SÉRIE
a) 10,2 km.
b) 4,50 km.
c) 14,7 km.
d) 5,70 km.
e) 6,00 km.
3) A velocidade é uma grandeza que relaciona a distância percorrida e o tempo gasto
para percorrê-la. A aceleração é uma grandeza que mede a rapidez com que a
velocidade varia. Mais rápido, mais lento, são percepções sensoriais. Tentamos medir
com relógios tais variações e nos rebelamos, quando elas não concordam com a nossa
percepção. Dizemos nunca com muita facilidade, dizemos sempre com muita facilidade,
como se fôssemos fiéis a um momento. “Mas o outro já está olhando para o lado.”
(LUFT, 2014)
O que é constante e imutável num momento não será mais no momento seguinte. Uma
velocidade, num momento, pode não ser a mesma num momento seguinte.
Assinale a situação em que o móvel apresenta maior valor (positivo ou negativo) de
aceleração:
a) O móvel estava a 50 m / s e manteve essa velocidade durante 2,0 s.
b) O móvel estava a 20 m / s e, em 10 s, aumentou a sua velocidade para 40 m / s.
c) O móvel estava a 10 m / s e, em 2,0 s, diminuiu sua velocidade para zero.
Página 2 de 18
LISTA EXTRA – 3ª SÉRIE
d) O móvel estava a 40m / s e, em 10 s, diminuiu sua velocidade para zero.
4) Em 2014, comemoraram-se os 50 anos do início da operação de trens de alta
velocidade no Japão, os chamados trens-bala. Considere que um desses trens desloca-se
com
uma
velocidade constante de 360 km / h sobre trilhos horizontais. Em um trilho paralelo,
outro trem desloca-se também com velocidade constante de 360 km / h, porém em
sentido
contrário.
Nesse caso, o módulo da velocidade relativa dos trens, em m / s. é Igual a
a) 50.
b) 100.
c) 200.
d) 360.
e) 720.
5)
A castanha-do-pará (Bertholletia excelsa) é fonte de alimentação e renda das
populações tradicionais da Amazônia. Sua coleta é realizada por extrativistas que
percorrem quilômetros de trilhas nas matas, durante o período das chuvas amazônicas.
A castanheira é uma das maiores árvores da floresta, atingindo facilmente a altura de
50m. O fruto da castanheira, um ouriço, tem cerca de 1kg e contém, em média, 16
sementes. Baseando-se nesses dados e considerando o valor padrão da aceleração da
gravidade 9,81m / s2, pode-se estimar que a velocidade com que o ouriço atinge o solo,
ao cair do alto de uma castanheira, é de, em m / s, aproximadamente,
a) 5,2.
b) 10,1.
c) 20,4.
d) 31,3.
e) 98,1.
6) Uma ave marinha costuma mergulhar de uma altura de 20 m para buscar alimento no
mar.
Página 3 de 18
LISTA EXTRA – 3ª SÉRIE
Suponha que um desses mergulhos tenha sido feito em sentido vertical, a partir do
repouso e exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de resistência do ar, a ave chegará à superfície do
mar a uma velocidade, em m/s, aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
7) No desenvolvimento do sistema amortecedor de queda de um elevador de massa m,
o engenheiro projetista impõe que a mola deve se contrair de um valor máximo d,
quando o elevador cai, a partir do repouso, de uma altura h, como ilustrado na figura
abaixo. Para que a exigência do projetista seja satisfeita, a mola a ser empregada deve
ter constante elástica dada por
Note e adote:
- forças dissipativas devem ser ignoradas;
- a aceleração local da gravidade é g.
a) 2 m g h  d / d2
b) 2 m g h  d / d2
c) 2 m g h / d2
d) m g h / d
e) m g / d
Página 4 de 18
LISTA EXTRA – 3ª SÉRIE
8) Uma pista de esqui para treinamento de principiantes foi projetada de modo que,
durante o trajeto, os esquiadores não ficassem sujeitos a grandes acelerações nem
perdessem contato com nenhum ponto da pista. A figura representa o perfil de um
trecho dessa pista, no qual o ponto C é o ponto mais alto de um pequeno trecho circular
de raio de curvatura igual a 10 m.
Os esquiadores partem do repouso no ponto A e percorrem a pista sem receber nenhum
empurrão, nem usam os bastões para alterar sua velocidade. Adote g  10 m / s2 e
despreze o atrito e a resistência do ar.
a) Se um esquiador passar pelo ponto B da pista com velocidade 10 2 m s, com que
velocidade ele passará pelo ponto C?
b) Qual a maior altura h A do ponto A, indicada na figura, para que um esquiador não
perca contato com a pista em nenhum ponto de seu percurso?
9) Um esquiador, com 70kg de massa, colide elasticamente contra uma árvore a uma
velocidade de 72km / h.
Calcule, em unidades do SI, o momento linear e a energia cinética do esquiador no
instante da colisão.
10) Um carro, em um trecho retilíneo da estrada na qual trafegava, colidiu frontalmente
com um poste. O motorista informou um determinado valor para a velocidade de seu
veículo no momento do acidente. O perito de uma seguradora apurou, no entanto, que a
velocidade correspondia a exatamente o dobro do valor informado pelo motorista.
Página 5 de 18
LISTA EXTRA – 3ª SÉRIE
Considere Ec1 a energia cinética do veículo calculada com a velocidade informada pelo
motorista e Ec 2 aquela calculada com o valor apurado pelo perito.
A razão
a)
1
2
b)
1
4
Ec1
corresponde a:
Ec 2
c) 1
d) 2
TEXTO PARA A PRÓXIMA QUESTÃO:
A figura abaixo mostra, de forma simplificada, o sistema de freios a disco de um
automóvel. Ao se pressionar o pedal do freio, este empurra o êmbolo de um primeiro
pistão que, por sua vez, através do óleo do circuito hidráulico, empurra um segundo
pistão. O segundo pistão pressiona uma pastilha de freio contra um disco metálico preso
à roda, fazendo com que ela diminua sua velocidade angular.
11) Qual o trabalho executado pela força de atrito entre o pneu e o solo para parar um
carro de massa m  1.000 kg, inicialmente a v  72 km / h, sabendo que os pneus travam
no instante da frenagem, deixando de girar, e o carro desliza durante todo o tempo de
frenagem?
a) 3,6  104 J.
Página 6 de 18
LISTA EXTRA – 3ª SÉRIE
b) 2,0 105 J.
c) 4,0 105 J.
d) 2,6 106 J.
TEXTO PARA A PRÓXIMA QUESTÃO:
Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com
dimensões comparáveis às da Terra, composta predominantemente de diamante. Por ser
muito frio, o astro, possivelmente uma estrela anã branca, teria tido o carbono de sua
composição cristalizado em forma de um diamante praticamente do tamanho da Terra.
12)
Os astrônomos estimam que a estrela estaria situada a uma distância
d  9,0 1018 m da Terra. Considerando um foguete que se desloca a uma velocidade
v  1,5  104 m / s, o tempo de viagem do foguete da Terra até essa estrela seria de
(1ano  3,0  107 s)
a) 2.000 anos.
b) 300.000 anos.
c) 6.000.000 anos.
d) 20.000.000 anos.
13) Os dois primeiros colocados de uma prova de 100 m rasos de um campeonato de
atletismo foram, respectivamente, os corredores A e B. O gráfico representa as
velocidades escalares desses dois corredores em função do tempo, desde o instante da
largada (t = 0) até os instantes em que eles cruzaram a linha de chegada.
Página 7 de 18
LISTA EXTRA – 3ª SÉRIE
Analisando as informações do gráfico, é correto afirmar que, no instante em que o
corredor A cruzou a linha de chegada, faltava ainda, para o corredor B completar a
prova, uma distância, em metros, igual a
a) 5.
b) 25.
c) 15.
d) 20.
e) 10.
14)
Algumas cidades têm implantado corredores exclusivos para ônibus a fim de diminuir o
tempo das viagens urbanas.
Suponha que, antes da existência dos corredores, um ônibus demorasse 2 horas e 30
minutos para percorrer todo o trajeto de sua linha, desenvolvendo uma velocidade
média de 6 km/h.
Página 8 de 18
LISTA EXTRA – 3ª SÉRIE
Se os corredores conseguirem garantir que a velocidade média dessa viagem aumente
para 20 km/h, o tempo para que um ônibus percorra todo o trajeto dessa mesma linha
será
a) 30 minutos.
b) 45 minutos.
c) 1 hora.
d) 1 hora e 15 minutos.
e) 1 hora e 30 minutos.
15) Correr uma maratona requer preparo físico e determinação. A uma pessoa comum
se recomenda, para o treino de um dia, repetir 8 vezes a seguinte sequência: correr a
distância de 1 km à velocidade de 10,8 km/h e, posteriormente, andar rápido a 7,2 km/h
durante dois minutos.
a) Qual será a distância total percorrida pelo atleta ao terminar o treino?
b) Para atingir a velocidade de 10,8 km/h, partindo do repouso, o atleta percorre 3 m
com aceleração constante. Calcule o módulo da aceleração a do corredor neste trecho.
16) O cérebro humano demora cerca de 0,36 segundos para responder a um estímulo.
Por exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de
resposta para acionar o freio.
Determine a distância que um carro a 100 km/h percorre durante o tempo de resposta do
motorista e calcule a aceleração média imposta ao carro se ele para totalmente em 5
segundos.
17) Filas de trânsito são comuns nas grandes cidades, e duas de suas consequências
são: o aumento no tempo da viagem e a irritação dos motoristas. Imagine que você está
em uma pista dupla e enfrenta uma fila. Pensa em mudar para a fila da pista ao lado,
pois percebe que, em determinado trecho, a velocidade da fila ao lado é 3 carros/min.
enquanto que a velocidade da sua fila é 2 carros /min.
Considere o comprimento de cada automóvel igual a 3 m.
Página 9 de 18
LISTA EXTRA – 3ª SÉRIE
Assinale a alternativa correta que mostra o tempo, em min, necessário para que um
automóvel da fila ao lado que está a 15m atrás do seu possa alcançá-lo.
a) 2
b) 3
c) 5
d) 4
18)
Sem proteção adequada, uma queda com skate pode causar sérias lesões,
dependendo da velocidade que ocorre a queda. Um menino em repouso no seu skate
encontra-se no ponto mais alto de uma rampa e começa a descer, chegando ao ponto
mais baixo com velocidade de módulo 2,0 m/s. Em seguida, o menino se lança para
baixo com o mesmo skate desse ponto mais alto com uma velocidade inicial de módulo
1,5 m/s.
Sabendo que, em ambas as situações, após iniciado o movimento, o menino não toca
mais os pés no solo, a alternativa correta que indica o módulo da velocidade, em m/s,
com que o menino no skate chega ao ponto mais baixo na segunda situação, é:
a) 0,5
b) 3,5
c) 2,5
d) 2,0
19) Tendo chegado atrasado ao casamento, um convidado conseguiu pegar uma última
fatia de bolo e concluiu que experimentara o melhor glacê de toda a sua vida. Ouvindo
falar que na cozinha havia mais um bolo, mas que seria cortado apenas em outra festa,
ele foi até lá. Viu o bolo em cima de uma mesa perto da porta. Porém, percebeu que
havia também uma cozinheira de costas para o bolo e para ele. Querendo passar o dedo
no bolo sem ser pego pela cozinheira e conseguir pegar a maior quantidade de glacê
possível, o convidado deduziu que, se passasse muito rápido, o dedo pegaria pouco
glacê; mas, se passasse muito lentamente, corria o risco de ser descoberto. Supondo,
Página 10 de 18
LISTA EXTRA – 3ª SÉRIE
então, que ele tenha 3 segundos para roubar o glacê sem ser notado e que a melhor
técnica para conseguir a maior quantidade seja passar o dedo por 40,5 cm de bolo em
MRUV, partindo do repouso, qual aceleração teria o dedo no intervalo de tempo do
roubo do glacê?
a) 0,03 m / s2
b) 0,04 m / s2
c) 0,09 m / s2
d) 1,05 m / s2
e) 2 m / s2
20) Em uma prova de atletismo, um corredor, que participa da prova de 100 m rasos,
parte do repouso, corre com aceleração constante nos primeiros 50 m e depois mantém a
velocidade constante até o final da prova.
Sabendo que a prova foi completada em 10 s, calcule o valor da aceleração, da
velocidade atingida pelo atleta no final da primeira metade da prova e dos intervalos de
tempo de cada percurso.
Apresente os cálculos.
21)
Suponha que um automóvel de motor muito potente possa desenvolver uma
aceleração média de módulo igual a 10 m/s2. Partindo do repouso, este automóvel
poderia chegar à velocidade de 90 km/h num intervalo de tempo mínimo, em segundos,
igual a:
a) 2,0.
b) 9,0.
c) 2,5.
d) 4,5.
e) 3,0.
22) A situação em que o módulo da aceleração média será maior está descrita em:
a) “Na Terra, uma pedra arremessada para cima encontra-se no ponto mais alto de sua
trajetória.”
b) “Um corredor velocista realiza a prova dos 100 m rasos alcançando a partir do
repouso a velocidade de 11 m/s em 5 s.”
Página 11 de 18
LISTA EXTRA – 3ª SÉRIE
c) “Um automóvel em movimento tem sua velocidade de 16 m/s reduzida a zero em 4 s
diante de um sinal vermelho.”
d) “Um avião, ao pousar, toca a pista de aterrissagem com uma velocidade inicial de 70
m/s, levando 14 s para alcançar o repouso.”
23) Um objeto tem a sua posição (x) em função do tempo (t) descrito pela parábola
conforme o gráfico.
Analisando-se esse movimento, o módulo de sua velocidade inicial, em m/s, e de sua
aceleração, em m/s2, são respectivamente iguais a
a) 10 e 20.
b) 10 e 30.
c) 20 e 10.
d) 20 e 30.
e) 30 e 10.
24)
Arnaldo e Batista disputam uma corrida de longa distância. O gráfico das
velocidades dos dois atletas, no primeiro minuto da corrida, é mostrado na figura.
Página 12 de 18
LISTA EXTRA – 3ª SÉRIE
Determine
a) a aceleração aB de Batista em t = 10 s;
b) as distâncias dA e dB percorridas por Arnaldo e Batista, respectivamente, até t = 50
s;
c) a velocidade média v A de Arnaldo no intervalo de tempo entre 0 e 50 s.
25) Uma pessoa do alto de um prédio solta uma bola e mede o módulo da posição da
bola em função do tempo. A figura, abaixo, mostra o esboço do gráfico da posição em
relação ao tempo.
Assinale a alternativa que representa o esboço dos gráficos em relação à velocidade 
tempo e à aceleração  tempo, respectivamente.
a)
b)
Página 13 de 18
LISTA EXTRA – 3ª SÉRIE
c)
d)
e)
26) Um corpo de massa m, em queda livre e sob ação de gravidade g constante, parte
do repouso e descreve uma trajetória vertical. Durante a queda, a resistência do ar impõe
uma força de atrito proporcional ao módulo V da velocidade do corpo, o que faz a
massa se deslocar com aceleração variável. O módulo da força de resistência é dado por
bV, onde b é uma constante de proporcionalidade e depende, dentre outros fatores, da
forma do corpo. A segunda Lei de Newton, aplicada ao corpo, mostra que o módulo da
força resultante é força = mg  bV  mA, onde A é o módulo da aceleração. Note que, no
instante inicial, V = 0 e a aceleração fica simplesmente A = g. À medida que o tempo
passa, V aumenta e A diminui até um instante de tempo em que a velocidade se manterá
constante. Esta velocidade, chamada de velocidade terminal, tem módulo igual a
a) mg.
b) bmg.
c) b/m.
Página 14 de 18
LISTA EXTRA – 3ª SÉRIE
d) mg/b.
27) Dois corpos de massas m e 2m são abandonados da mesma altura, ambos com
velocidade inicial nula. Durante a queda de ambos, a aceleração gravitacional é
constante e a resistência do ar desprezível. Sendo t1 e t2 , respectivamente, o tempo que
cada corpo leva para atingir o solo, a relação entre esses tempos é
a) t1  2,00 t 2.
b) t1  0,50 t 2.
c) t1  0,25 t 2.
d) t1  1,00 t2.
e) t1  4,00 t 2.
28) Um professor utiliza essa história em quadrinhos para discutir com os estudantes o
movimento de satélites. Nesse sentido, pede a eles que analisem o movimento do
coelhinho, considerando o módulo da velocidade constante.
Página 15 de 18
LISTA EXTRA – 3ª SÉRIE
Desprezando a existência de forças dissipativas, o vetor aceleração tangencial do
coelhinho, no terceiro quadrinho, é
a) nulo.
b) paralelo à sua velocidade linear e no mesmo sentido.
c) paralelo à sua velocidade linear e no sentido oposto.
d) perpendicular à sua velocidade linear e dirigido para o centro da Terra.
e) perpendicular à sua velocidade linear e dirigido para fora da superfície da Terra.
29)
As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem substituir
dezenas de trabalhadores rurais, o que pode alterar de forma significativa a relação de
trabalho nas lavouras de cana-de-açúcar. A pá cortadeira da máquina ilustrada na figura
abaixo gira em movimento circular uniforme a uma frequência de 300 rpm. A
velocidade de um ponto extremo P da pá vale
Página 16 de 18
LISTA EXTRA – 3ª SÉRIE
(Considere π  3. )
a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
30) Da parte superior de um caminhão, a 5,0 metros do solo, o funcionário 1 arremessa,
horizontalmente, caixas para o funcionário 2, que se encontra no solo para pegá-las. Se
cada caixa é arremessada a uma velocidade de 8,0 m/s, da base do caminhão, deve ficar
o funcionário 2, a uma distância de
Considere a aceleração da gravidade 10,0 m/s2 e despreze as dimensões da caixa e dos
dois funcionários.
a) 4,0 m.
b) 5,0 m.
c) 6,0 m.
d) 7,0 m.
e) 8,0 m.
Página 17 de 18
LISTA EXTRA – 3ª SÉRIE
Página 18 de 18