EXERCÍCIOS – Provas anteriores de COB 781 – Professor

EXERCÍCIOS – Provas anteriores de COB 781 – Professor Macoto
1) Calcule os valores mais alto e mais baixo de C necessários para sintonizar juntamente
com uma bobina de 0,1µH a faixa dede radiodifusão comercial de FM entre 88 e 108MHz
(a freqüência de sintonia é caracterizada pelo fator ω0 do circuito RLC).
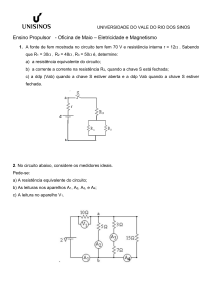
2) Um circuito ca (corrente alternada) com RL paralelo, tem uma tensão de pico de 100V
aplicada através de R=20Ω e XL=20Ω. Calcule IR, IL, IT e θ. Desenhe os diagramas de
fasores de tempo de vT, iR e iT.
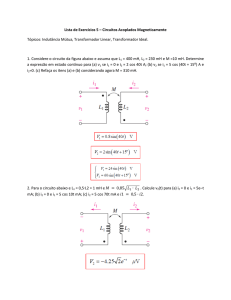
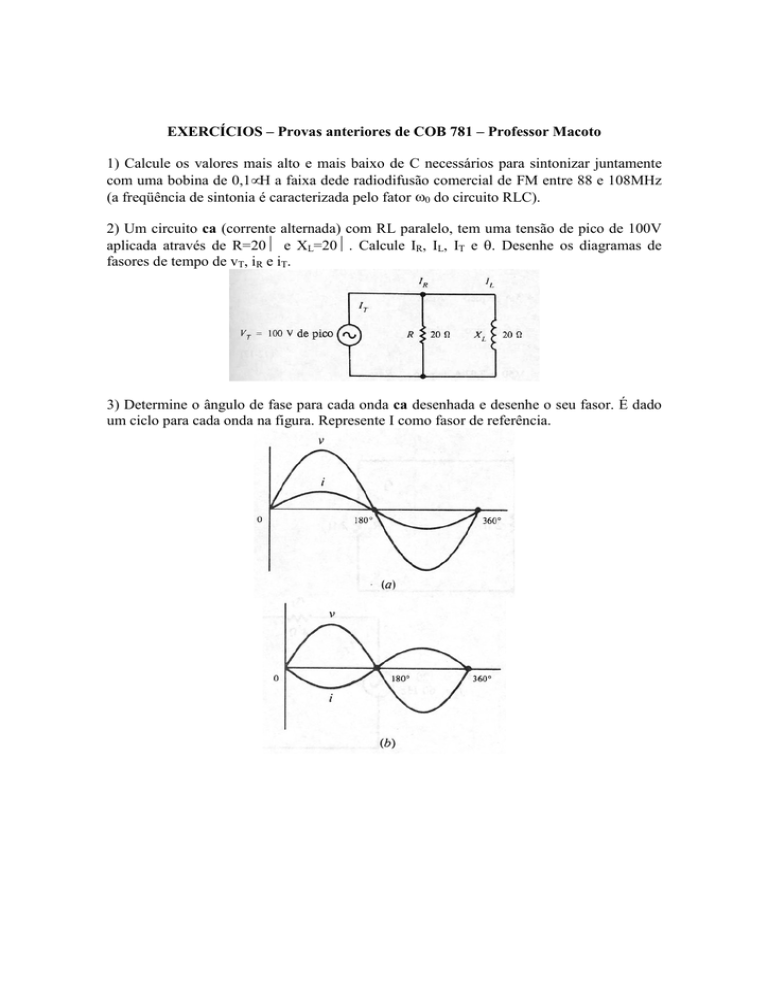
3) Determine o ângulo de fase para cada onda ca desenhada e desenhe o seu fasor. É dado
um ciclo para cada onda na figura. Represente I como fasor de referência.
4) Num estágio com acoplamento resistivo, a queda de tensão entre os pontos A e B é de
14,4V. Se a freqüência da corrente for de 1kHz, calcule a tensão através do resistor.
Desenhe o diagrama de fasores.
5) Para o circuito RLC série, calcule XL, XC, Z, I, VR, VL, VC, P e FP. Faça o diagrama de
fasores para a tensão.
6) Uma associação RL série num circuito ca tem R=10Ω e XL=12Ω. Liga-se um capacitor
através da associação (ver figura). Qual deverá ser a reatância do capacitor se o circuito
tiver que ter um FP de uma unidade?
7) Calcule a tensão v(t) no circuito abaixo.
8) Resolver o circuito pelo método das malhas obtendo os fasores I1 e I2.
9) Uma combinação em série de uma resistência e um capacitor produz uma corrente de 2A
atrasada da tensão aplicada de 80º. Se o módulo da tensão aplicada é 110V (60Hz), quais
são os valores da resistência e capacitor?
10) Determine: (a) a corrente total It e (b) a tensão V1 .Considere R1= 10Ω, R2= 10Ω,
R3= 10Ω, XC1= -j20Ω, XC2= -j10Ω e XL= j10Ω.
EXERCÍCIOS – Listas de Exercícios de Circuitos 1 (UFRJ) - Antonio Petraglia
1) Para o circuito mostrado, sabendo que vs (t ) = 100 ⋅ cos(2 ⋅ π ⋅ 500 ⋅ t ) , e vo(t) é a tensão
sobre o resistor de 3KΩ:
a) Calcule vo(t) para regime permanente
b) Qual o período de vo(t)?
c) A resposta está atrasada ou adiantada em relação à vs(t)?
d) Qual o valor do atraso/avanço?
rta.: a) vo(t ) = 98,9 ⋅ cos(2 ⋅ π ⋅ 500 ⋅ t + 0,6) , b) 2ms, c) adiantada, d) 16,23µs
2) Calcule no circuito ao lado a tensão sobre o indutor em regime permanente senoidal para
vf (t ) = cos(2000 ⋅ t − π / 4)
rta.: v(t ) = 0,95 ⋅ cos(2000 ⋅ t − 0,465)V
3) Um circuito RL série, com resistor de 8Ω e indutância de 3H é conectado em série com
uma fonte de tensão de valor vs (t ) = 10 ⋅ 2 ⋅ cos(10 ⋅ t + π / 4 )V . O circuito está em regime
permanente. Calcule:
a) O fasor que representa a corrente.
b) A corrente instantânea i(t).
c) A potência p(t) fornecida pela fonte de tensão.
d) O atraso (ou avanço) em segundo da corrente em relação à tensão.
rta.: a) I = 0,45 ∠ − 0,52 , b) i(t ) = 0,45 ⋅ cos(10 ⋅ t − 0,52)A
c) p(t ) = 3,44 + 3,18 ⋅ cos(20 ⋅ t + 0,26) , d) ∆t = 0,13s
TABELA COM VALORES DE tan(θ)
θ(graus)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Tan(θ)
0
0,017455
0,034921
0,052408
0,069927
0,087489
0,105104
0,122785
0,140541
0,158384
0,176327
0,19438
0,212557
0,230868
0,249328
0,267949
0,286745
0,305731
0,32492
0,344328
0,36397
0,383864
0,404026
0,424475
0,445229
0,466308
0,487733
0,509525
0,531709
0,554309
θ(graus)
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
Tan(θ)
0,57735
0,600861
0,624869
0,649408
0,674509
0,700208
0,726543
0,753554
0,781286
0,809784
0,8391
0,869287
0,900404
0,932515
0,965689
1
1,03553
1,072369
1,110613
1,150368
1,191754
1,234897
1,279942
1,327045
1,376382
1,428148
1,482561
1,539865
1,600335
1,664279
θ(graus)
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
Tan (θ)
1,732051
1,804048
1,880726
1,962611
2,050304
2,144507
2,246037
2,355852
2,475087
2,605089
2,747477
2,904211
3,077684
3,270853
3,487414
3,732051
4,010781
4,331476
4,70463
5,144554
5,671282
6,313752
7,11537
8,144346
9,514364
11,43005
14,30067
19,08114
28,63625
57,28996
infinito