Elasticidades de uma Função Cobb

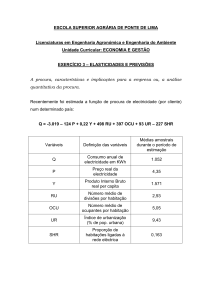
Microeconomia
Elasticidades:
Função Utilidade Cobb-Douglas
Prof.: Antonio Carlos Assumpção
Elasticidades: Cobb-Douglas
Suponha que as preferências de um consumidor possam ser
representadas por U ( x, y ) = xα y β .
Podemos encontras as
demandas Marshalianas da seguinte forma:
lagrangeano → ℑ = xα y β + λ ( I − Px x − Py y )
Cond . de primeira ordem :
∂ℑ
= 0 ⇒ α xα −1 y β − λ Px = 0
∂x
∂ℑ
= 0 ⇒ β xα y β −1 − λ Py = 0
∂y
∂ℑ
= 0 ⇒ I − Px x − Py y = 0
∂λ
α y Px
β
=
⇒ Py y = Px x
Logo :
β x Py
α
Elasticidades: Cobb-Douglas
α y Px
β
Logo :
=
⇒ Py y = Px x
β x Py
α
Substituindo na R.O.I .
β
β
β
I

I = Px x + Py y ⇒ Px x + Px x = I ⇒ Px x  1 +  = I ⇒
= 1+
α
Px x
α
 α
I
α +β
I
=
⇒ Px x =
⇒
α +β
α
Px x
α
α
I
∗
x =
Demanda Marshaliana Pelo Bem X
α
β
P
+
(
) x
Elasticidades: Cobb-Douglas
Elasticidade Preço da Demanda por X
Demanda por x
EPXX
E
X
PX
x∗ =
α
I
α
⇒ x∗ =
IPx−1
(α + β ) Px
(α + β )






P
P
∂X
α
−2 
−1
x
X

IP
P
=
•
⇒ −
•
⇒
−
x Px ⇒
 x 
∂PX X
 α  −1 
α + β 
  α + β  IPx 



= −1
Logo, para uma função utilidade Cobb-Douglas, preço e
quantidade variam na mesma proporção, ou seja, um aumento no
preço do bem x de 1% reduz a quantidade demandada em 1%.
OBS. De forma equivalente, poderíamos calcular a elasticidade preço
da demanda por y, que também é igual a um (em módulo).
Elasticidades: Cobb-Douglas
Elasticidade Renda da Demanda por X
Demanda por x
 α 1
∂X I
E =
• ⇒
 •
∂I X
 α + β  Px
X
I
X
I
E =1
α
I
x =
(α + β ) Px
∗
 α  I (α + β ) Px
⇒
•
⇒

α
I
αI
 α + β  Px
(α + β ) Px
I
Logo, para uma função utilidade Cobb-Douglas, renda e quantidade
variam na mesma proporção, ou seja, um aumento na renda de 1%
aumenta a demanda por x em 1%.
OBS. De forma equivalente, poderíamos calcular a elasticidade renda
da demanda por y, que também é igual a um.
Elasticidades: Cobb-Douglas
Elasticidade Cruzada da Demanda por X
Demanda por x
X
( x ,y)
E
α
I
x =
(α + β ) Px
∗
Py
∂X Py
=
• ⇒ 0• = 0
∂Py X
X
E(Xx,y) = 0
Logo, para uma função utilidade Cobb-Douglas, a variação
no preço de y não afeta a quantidade demandada pelo bem x.
OBS. De forma equivalente, poderíamos calcular a elasticidade
cruzada da demanda por y, que também é igual a zero.
Elasticidades: Cobb-Douglas
Logo, para uma função utilidade Cobb-Douglas,
as elasticidades preço e renda são unitárias e as
elasticidades cruzadas iguais a zero.