Apostila CCE v7(+simobologia)

UNIVERSIDADE DO ESTADO SANTA CATARINA
PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA
ELÉTRICA
Apostila da Disciplina de Controle de Conversores Estáticos
Prof. Alessandro Luiz Batschauer
Joinville
2012
Dedicatória
À minha esposa,
À minha família e aos amigos.
Aos professores do NPEE e aos alunos de pós-graduação que
contribuíram na escrita e concepção deste documento.
Sumário
1
Introdução Geral
1
1.1 Introdução____________________________________ 1
2
Conceitos de Modulação por Largura de
PulsosEquation Section (Next)[1]
3
2.1 Parêmtros da Modulação PWM ___________________ 3
2.1.1 Sinal de Referência ________________________ 3
2.1.2 Sinal de Portadora _________________________ 5
2.1.3 Modulador (Comparador) ___________________ 6
2.1.4 Geração de sinal complementar _______________ 7
2.1.5 Tempo Morto _____________________________ 8
2.2 Modulações para conversores cc-ca ________________ 9
2.2.1 Modulação por largura de pulso único ________ 10
2.2.2 Modulações PWM senoidais ________________ 13
2.2.3 Modulação Pwm Senoidal Bipolar ___________ 14
2.2.4 Modulação Pwm Senoidal Unipolar __________ 16
2.2.5 Modulação PWM Senoidal Por Portadora Com
Simetria De Um Quarto De Onda __________________ 21
2.2.6 Modulação PWM Senoidal Dipolar __________ 22
2.3 Modulação com Três ou Mais Níveis ______________ 25
2.3.1 Modulação com Portadoras Dispostas em Fase
(Phase Disposition – PD) ________________________ 25
2.3.2 Modulação com as Portadoras Dispostas em
Oposição de Fase (Phase Opposition Disposition – POD)
26
2.3.3 Modulação com as Portadoras Dispostas em
Oposição Alternada de Fase (Alternative Opposition
Disposition – APOD) ___________________________ 27
2.3.4 Modulação com as Portadoras com Deslocamento
de Fase (Phase Shifted – PS) _____________________ 28
2.3.5 Comparação Entre as Modulações ___________ 29
2.3.6 Exemplo de Modulação Híbrida _____________ 33
2.4 Modulação SHE ______________________________ 37
2.5 Modulação por Vetores Espaciais ________________ 37
2.6 Conclusão ___________________________________ 38
3
Revisão
dos
Conceitos
Básicos
de
ControleEquation Section (Next)
40
3.1 Ações básicas dos controladores P, I, PI, PID _______ 40
3.2 Conceito de pólo, zero, estabilidade ______________ 40
3.2.1 Diagrama de bode________________________ 40
3.2.2 Margem de fase _________________________ 58
3.2.3 Lugar das raízes _________________________ 65
4
Modelagem do conversor BUCK em condução
contínuaEquation Section (Next)
75
4.1 Introdução __________________________________ 75
4.2 Modelagem do Conversor BUCK em Modo de Condução
Contínua _______________________________________ 75
4.3 Modelo de Tensão do Conversor BUCK v(s) / d(s) __ 81
4.3.1 Simulação da Planta de tensão em função da razão
cíclica V(s) / d(s) ______________________________ 84
4.4 Modelo de Corrente do Conversor BUCK I0(s) / d(s) _ 87
4.4.1 Simulação da Planta de corrente em função da
razão cíclica I0(s) / d(s) ___________________________ 89
4.5 Modelo de Tensão em função da Corrente do Conversor
BUCK V(s) / I0(s) ________________________________ 91
4.5.1 Simulação da Planta de tensão em função da
corrente V(s) / I0(s) ____________________________ 93
4.6 Conclusões _________________________________ 95
5
Modelagem do conversor BOOST em condução
contínuaEquation Section (Next)
96
5.1 INTRODUÇÃO _____________________________ 96
5.2 CONVERSOR BOOST _______________________ 96
5.3 MODELO CONVERSOR _____________________ 99
5.3.1 Etapas de Operação BOOST condução contínua 99
5.3.2 Modelagem de pequenos sinais ____________ 100
5.3.3 Simulações ____________________________ 105
5.4 Conclusão _________________________________ 113
6
Modelagem do conversor BUCK-BOOST em
condução contínua
114
6.1 Introdução _________________________________ 114
6.2 Conversor buck-boost ________________________ 114
6.2.1 Primeira etapa__________________________ 115
6.2.2 Segunda etapa__________________________ 117
6.2.3 Valores médios em um período de comutação _ 118
6.2.4 Corrente média no capacitor ______________ 120
6.2.5 Perturbações ___________________________ 121
6.2.6 Termos constantes ______________________ 124
6.2.7 Transformada de Laplace _________________ 124
6.2.8 Plantas do conversor _____________________ 125
6.3 Validação das plantas _________________________ 131
6.3.1 Parameter File __________________________ 131
6.3.2 AC Sweep _____________________________ 135
6.3.3 s-domain Transfer Function________________ 138
6.3.4 Validação da planta de tensão e corrente pela razão
cíclica 140
6.3.5 Validação da planta de tensão e corrente pela tensão
de entrada ___________________________________ 145
6.4 Conclusões _________________________________ 149
7
Modelagem do conversor BUCK-BOOST em
condução descontínuaEquation Section (Next)
149
7.1 Introdução__________________________________ 149
7.2 Modelo médio dos interruptores _________________ 150
7.2.1 Determinação dos valores médios ___________ 151
7.2.2 Construção do circuito equivalente __________ 155
7.2.3 Modelo para pequenos sinais_______________ 158
7.3 Simulação do Conversor Buck-Boost ____________ 165
7.4 Conclusão __________________________________ 168
8
Modelagem de conversor BUCK-BOOST
169
8.1 Controle de Conversores ______________________ 169
8.1.1 Critérios para o projeto de controladores de
conversores estáticos no domínio da frequência ______ 169
8.1.2 Introdução ao uso do SISOTOOL ___________ 169
8.1.3 Controle do Conversor Buck MCC __________ 175
8.1.4 Controle do Conversor Boost CCM _________ 201
8.1.5 Conclusões_____________________________ 225
Lista de Figuras
Fig. 2.1 – Modulação com as portadoras dispostas em fase (Phase
Disposition – PD).................................................................................. 26
Fig. 2.2 – Exemplo de modulação com as portadoras dispostas em
oposição de fase (Phase Opposition Disposition – POD). .................... 26
Fig. 2.3 – Exemplo de modulação com as portadoras dispostas em
oposição alternada de fase (Alternative Phase Opposition Disposition –
APOD). ................................................................................................. 27
Fig. 2.4 – Exemplo de modulação com as portadoras com
deslocamento de fase (Phase Shifted – PS)........................................... 28
Fig. 2.5 – “Modulação PWM senoidal padrão” (Standard
Sinusoidal Pulsewidth Modulation – SPWM) com injeção de
componentes de sequência zero. ........................................................... 34
Fig. 2.6 – “Modulação PWM com dupla referência” (DoubleSignal Pulsewidth Modulation – DSPWM). ......................................... 35
Fig. 2.7 – Modulação híbrida proposta por Zaragoza (Hybrid
Pulsewidth Modulation – HPWM). ...................................................... 36
Fig. 2.8 – Exemplo de modulação híbrida empregando
frequências distintas para cada célula de conversor em ponte completa.
(a) Tensão de saída sintetizada por um dos inversores. (b) Sinal de
referência e portadoras empregadas para determinar os pulsos de
comando do segundo inversor............................................................... 37
Fig. 8.1 - Janela “Control and estimation Tool Manager”........ 170
Fig. 8.2 - Opções de unidade SISOTOOLS ............................. 171
Fig. 8.3 - Aparência dos compensadores .................................. 171
Fig. 8.4- Seleção da arquitetura de controle ............................. 171
Fig. 8.5 - Edição dos dados da planta ....................................... 171
Fig. 8.6 - Edição do compensador ............................................ 172
Fig. 8.7 - Opções de ajuste gráfico ........................................... 173
Fig. 8.8 - Ajuste gráfico do compensador – planta original ..... 174
Fig. 8.9 - situação da planta após a edição do compensador .... 174
Fig. 8.10 – Malha de controle da tensão de saída do conversor
Buck. ................................................................................................... 175
Fig. 8.11 – Diagrama de Bode da FTMA da planta de controle de
tensão Buck sem compensação. .......................................................... 177
Fig. 8.12 - Diagrama de Bode da FTMA da planta de controle de
tensão Buck com compensação........................................................... 178
Fig. 8.13 – Tensão de saída (em vermelho) e referência (azul)
para degrau de +15%. ......................................................................... 179
Fig. 8.14 - Tensão de saída (em vermelho) e referência (azul)
para degrau de -15%............................................................................ 180
Fig. 8.15 – Tensão de saída (vermelho) e referência senoidal de 1
kHz (azul). ........................................................................................... 180
Fig. 8.16 - Malha de controle da corrente do indutor do conversor
Buck. ................................................................................................... 181
Fig. 8.17 - Diagrama de Bode da FTMA da planta de controle de
corrente do conversor Buck sem compensação. .................................. 182
Fig. 8.18 - Diagrama de Bode da FTMA da planta de controle de
corrente do conversor Buck com compensação. ................................. 183
Fig. 8.19 – Corrente no indutor (vermelho) e referência (azul)
para degrau de +15%. .......................................................................... 184
Fig. 8.20 - Corrente no indutor (vermelho) e referência (azul)
para degrau de -15%............................................................................ 185
Fig. 8.21 - Corrente no indutor (vermelho) e referência senoidal
de 1 kHz (azul). ................................................................................... 186
Fig. 8.22 - Malha de controle de corrente e tensão do conversor
Buck. ................................................................................................... 186
Fig. 8.23 – Diagrama de Bode da FTMA da planta de controle de
tensão do conversor Buck sem compensação considerando FTMFi
simplificada. ........................................................................................ 188
Fig. 8.24 – Diagrama de Bode da FTMA da planta de controle de
tensão do conversor Buck sem compensação considerando FTMFi
completa. ............................................................................................. 189
Fig. 8.25 – Diagrama de Bode da FTMA da planta de controle de
tensão do conversor Buck com compensação. .................................... 190
Fig. 8.26 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 191
Fig. 8.27 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 192
Fig. 8.28 – Tensão de saída (vermelho) e referência senoidal de 1
kHz (azul). ........................................................................................... 192
Fig. 8.29 – quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente de referência (verde) e
Tensão na entrada do modulador (Roxo) para redução de 50% da carga.
............................................................................................................. 194
Fig. 8.30 – Tensão de saída (vermelho) e referência (azul) para
incremento de 50% da carga. .............................................................. 195
Fig. 8.31 – Malha de controle do converso Buck em modo
corrente................................................................................................ 195
Fig. 8.32 - Diagrama de Bode da FTMA da planta de controle em
modo corrente do conversor Buck sem compensação. ....................... 196
Fig. 8.33 - Diagrama de Bode da FTMA da planta de controle em
modo corrente do conversor Buck com compensação. ....................... 197
Fig. 8.34 - Circuito simulado no PSIM para avaliação do controle
em modo corrente do conversor Buck ................................................ 198
Fig. 8.35 - Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 198
Fig. 8.36 -Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 199
Fig. 8.37 – Tensão de saída (vermelho) e referência senoidal de 1
kHz (azul). .......................................................................................... 200
Fig. 8.38 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente na saída do sensor (roxo) e
limite do controlador (verde) para redução de 50% da carga............ 200
Fig. 8.39 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente na saída do sensor (roxo) e
limite do controlador (verde) para aumento de 50% da carga. ......... 201
Fig. 8.40 - Malha de controle de tensão do conversor Boost ... 202
Fig. 8.41 – Diagrama de bode da FTMA do controle de tensão do
conversor Boost sem compensação..................................................... 203
Fig. 8.42 - Diagrama de bode da FTMA do controle de tensão do
conversor Boost compensada. ............................................................. 204
Fig. 8.43 – Tensão de saída (em vermelho) e referência (azul)
para degrau de +15%. ......................................................................... 205
Fig. 8.44 – Tensão de saída (em vermelho) e referência (azul)
para degrau de -15%. .......................................................................... 206
Fig. 8.45 – Tensão de saída (vermelho) e referência senoidal de
100 Hz (azul)....................................................................................... 206
Fig. 8.46 – Malha de controle de corrente do conversor Boost. 207
Fig. 8.47 - Diagrama de Bode da FTMA do controle de corrente
do conversor Boost sem compensação................................................ 207
Fig. 8.48 - Diagrama de Bode da FTMA do controle de corrente
do conversor Boost com compensação. .............................................. 208
Fig. 8.49 – Corrente no indutor (vermelho) e referência (azul)
para degrau de +15%. ......................................................................... 209
Fig. 8.50 - Corrente no indutor (vermelho) e referência (azul)
para degrau de -15%. .......................................................................... 210
Fig. 8.51 – Corrente no indutor (vermelho) e referência senoidal
de 1 kHz (azul). ................................................................................... 210
Fig. 8.52 – Diagrama de controle de corrente e tensão do
conversor Boost MCC ......................................................................... 211
Fig. 8.53 – Diagrama de Bode da FTMA da planta de corrente
simplificada do conversor Boost. ........................................................ 212
Fig. 8.54 - Diagrama de Bode da FTMA da planta de corrente
simplificada do conversor Boost com compensação. .......................... 212
Fig. 8.55 – Diagrama de Bode da FTMA da planta de tensão do
conversor Boost para o controle em cascata........................................ 214
Fig. 8.56 – Diagrama de Bode da FTMA da planta de tensão
compensada do conversor Boost para o controle em cascata. ............. 215
Fig. 8.57 – Tensão de saída (vermelho) e referência (azul) para
degrau de +15%................................................................................... 216
Fig. 8.58 – Tensão de saída (vermelho) e referência (azul) para
degrau de -15%. .................................................................................. 216
Fig. 8.59 Quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente no indutor para degrau de
+/- 50% da carga ................................................................................. 217
Fig. 8.60 – Tensão de saída (vermelho) e referência senoidal de
500 Hz (azul). ...................................................................................... 218
Fig. 8.61 – Malha de controle do converso Boost em modo
corrente................................................................................................ 218
Fig. 8.62 - Diagrama de Bode da FTMA da planta de controle em
modo corrente do conversor Boost sem compensação. ....................... 219
Fig. 8.63 - Diagrama de Bode da FTMA da planta de controle em
modo corrente do conversor Boost com compensação. ...................... 220
Fig. 8.64 - Circuito simulado no PSIM para avaliação do controle
em modo corrente do conversor Boost ................................................ 221
Fig. 8.65 - Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 222
Fig. 8.66 - Quadro superior: Tensão de saída (vermelho) e
referência (azul) .................................................................................. 223
Fig. 8.67 – Tensão de saída (vermelho) e referência senoidal de 1
kHz (azul). ........................................................................................... 223
Fig. 8.68 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente na saída do sensor (roxo) e
limite do controlador (verde) para redução de carga de 50% ........... 224
Fig. 8.69 – Quadro superior: Tensão de saída (vermelho) e
referência (azul) Quadro inferior: Corrente na saída do sensor (roxo) e
limite do controlador (verde) para aumentos de carga de 50% ........ 225
Lista de Tabelas
Tabela 2.1 – Comparação das distorções harmônicas e das perdas
de comutação entre as modulações PD, POD, APOD e PS para um
inversor trifásico em cascata com cinco níveis. .................................... 33
Tabela 2.2 – Comparação entre as modulações SPWM e DSPWM
.............................................................................................................. 35
Tabela 3 - Especificações do conversor ................................... 131
Tabela 4 – Parâmetros do modelo de pequenos sinais das chaves
em MCD. ............................................................................................ 163
Tabela 5 – Parâmetros utilizados para a simulação. ................. 165
Tabela 8.1 - Parâmetros do conversor Buck............................. 175
Tabela 8.2 – Coeficientes do controlador de tensão do conversor
Buck. ................................................................................................... 178
Tabela 8.3 – Coeficientes do controlador de corrente do
conversor Buck. .................................................................................. 183
Tabela 8.4 – Coeficientes do controlador de tensão do controle
em cascata do conversor Buck. ........................................................... 190
Tabela 8.5 – Coeficientes do controlador de tensão do controle
em modo corrente do conversor Buck. ............................................... 197
Tabela 8.6 - Parâmetros do conversor Boost ............................ 201
Tabela 8.7 – Coeficientes do controlador de tensão do conversor
Boost. .................................................................................................. 204
Tabela 8.8 – Coeficientes do controlador de corrente do
conversor Boost. ................................................................................. 208
Tabela 8.9 – Coeficientes do controlador de corrente para o
controle em cascata do conversor Boost. ............................................ 213
Tabela 8.10 – Coeficientes do controlador de tensão do controle
em cascata do conversor Boost. .......................................................... 214
Tabela 8.11 – Coeficientes do controlador de tensão do controle
em modo corrente do conversor Buck. ............................................... 220
Simbologia
Símbolos adotados nos Equacionamentos
Símbolo
Am
Descrição
Amplitude da onda moduladora
Unidade
V
Ap
Amplitude da onda portadora
V
An , A0
-
Bn , B0
Coeficientes do numerador
Valor de pico da componente harmônica de ordem
“n” da forma de onda
Componente fundamental da tensão de saída do
inversor 3 níveis
Coeficientes do denominador
C ( s ), R( s )
Função de transferência de malha fechada
-
C (s)
Controlador/Compensador
-
C 2( s )
DHT
D
d (t )
Controlador de tensão do controle em cascata
Distorção Harmônica Total
Valor da razão cíclica
Valor da razão cíclica
-
d (s)
d i (t )
Razão cíclica
-
Pequenos sinais de razão cíclica (perturbação)
Subintervalos (representa razão cíclica do
conversor)
Coeficiente de amortecimento
Coeficiente de amortecimento
-
bn
b1
d1 (t ), d 2 (t ), d 3 (t )
ξ
ξi
ξR
E
e(t )
e( s )
fp
fm
fo
fc
f1 , f 2
FTMAbv
-
-
Coeficiente de amortecimento
Tensão de entrada do conversor boost
Tensão de entrada do conversor boost
Variação na razão cíclica sobre a corrente no
indutor
Freqüência da onda portadora
V
V
Hz
Freqüência da onda moduladora senoidal
Hz
Freqüência fundamental de saída
Hz
-
Freqüência de comutação
Hz
Freqüência de chaveamento
Hz
Função de transferência de malha aberta
-
FTMA1
FTMF1
G1 ( s ), H1 ( s )
G ( jω )
GM
G ( jω ), H ( jω )
GPWM
Gv ( s), Gi ( s),
Givg ( s), Gvvg ( s)
g1
Gvd
Gd 0
H i (s)
Função de transferência de malha aberta
-
Função de transferência de malha fechada
-
Função de transferência de malha aberta
-
Função de transferência genérica
-
Margens de ganho
-
Função de transferência
-
Função de transferência do modulador por largura
de pulso
Plantas de variação da razão cíclica
-
Plantas de variação da razão cíclica
-
Parâmetros da função de transferência
Ganho da função de transferência da saída para
razão cíclica
Ganho da função de transferência da saída para
entrada
Função de transferência de corrente
-
H v ( s)
ic
iL
ir
ig
Função de transferência de tensão
-
Corrente no capacitor
A
Corrente no indutor
A
Corrente no resistor
A
Corrente da fonte de entrada
A
icmed
i pk
Corrente média do capacitor
A
Corrente de pico
A
i1 (t )
i2 (t )
< i1 (t ) >
I L (t )
Io
j1
Corrente na entrada
A
Ko
K
K1
Corrente no diodo
A
Corrente média nos terminais
A
Corrente no indutor
A
Corrente de saída
A
Parâmetros da função de transferência
Ganho da função de transferência determinado na
freqüência ω =1rad/s
Valor de ganho do sistema
Ajuste de ganho
-
L
Mi
Mf
Indutor/indutância
Índice de modulação (profundidade)
H
-
Modulação de freqüência
-
ma
m
n
n
n
pj
Índice de modulação de amplitude
Número de zeros
Numero de pólos
Ordem da função de transferência
Ordem da componente harmônica
Numero de pólos da função de transferência
-
pR , z R
Po
< p(t ) >Ts
q1
q2
r1 , r2
Ro
Re
r1
r2
Ω
T1 ( s )
T
Ts
Tc
Vi
V1
Vo
Pólos e zeros reais
-
Potência de saída
W
Potência média
Área da corrente i1 (t ) durante o intervalo t1
A.s
Área da corrente i2 (t ) no intervalo t2
A.s
Pontos de partida (do LGR)
-
Resistor
Ω
Ω
Ω
Ω
Hz
S
S
V
V
V
Vn
va , vb , vc
'
a
'
b
'
c
v ,v ,v
vo
vi
vip
Resistência efetiva
Resistência de entrada para pequenos sinais
Resistência de saída
Freqüência
Função de transferência de malha fechada
Período
Período de comutação
Razão cíclica multiplicada pelo período DTs
Tensão de entrada
Tensão fundamental para modulação bipolar
Nível médio presente na tensão ca
Amplitude da componente harmônica de tensão de
ordem “n”
Tensão das fases A,B,C
Tensão das fases A,B,C modificadas pela
seqüência zero
Tensão de seqüência zero
W
V
V
V
V
Sinais de referência,onde i pode ser as fases A,B,C
-
Sinais de referência positiva do modulador
-
vin
Vg
DSPWM
Sinais de referência negativa do modulador
DSPWM
Tensão de entrada
V
Tensão de saída
V
-
V
VL
Vc
vg
Tensão no indutor
V
Tensão no capacitor
V
Tensão da fonte de entrada
V
V( s )
Planta de tensão
V
v( s )
Vo
vLmed
Vm
Vc
v1 (t )
vi (t )
V1
Tensão de saída
V
Tensão de saída
V
< v1 (t ) >, < v2 (t ) >
WTHD
Wcg
Wcp
y1
Zi
α
φ
γ
ω0dB
γ
σo
ωp
Tensão média no indutor
V
Tensão de pico a pico da portadora
V
Tensão no componente
V
Tensão de entrada
V
Pequenos sinais alternados (perturbações)
V
Tensão média aplicada no transistor
V
Tensões médias nos terminais
V
Distorção harmônica total de primeira ordem
Freqüência de cruzamento de ganho
Freqüência de cruzamento de fase
Erro em regime para entrada do tipo degrau
unitário
Impedância
Ângulo da modulação por largura de pulso única
Fase da função de transferência
Numero de zeros ou pólos na origem
Freqüência em que o modulo de G ( jω ), H ( jω ) é
igual a 1
Ângulo formado entre a reta e o eixo real
Ponto onde a reta intercepta o eixo real
Hz
Hz
Rad
-
Freqüência de corte do pólo
Rad/s
-
Ω
Rad
Rad
Hz
Símbolos Usados para Referenciar Elementos de Circuitos
Símbolo
C
D
L
R
S
Descrição
Capacitor
Diodo
Indutor
Resistor
Interruptor
Símbolos de Unidades de Grandezas Físicas
Símbolo
A
H
V
W
Ω
Descrição
Ampère
Henry
Volt
Watt
Ohm
Introdução Geral
1
1
1.1
Introdução Geral
Introdução
O processamento eletrônico da energia elétrica está cada vez mais
presente nas residencias, no comércio, indústria, na geração de energia,
enfim, no dia a dia das pessoas de um modo geral, independente da
profissão desempenhada.
A geração de energia elétrica a partir de fontes renováveis como a
energia dos ventos (aerogeradores), a solar (painéis fotovoltaicos), o
hidrogênio (células combustível), bem como o armazenamento de
energia em supercapacitores, sistemas de massa girante (Flywheel),
baterias, entre outros, empregam conversores estáticos no
processamento da energia. O acionamento de sistemas motrizes como os
empregados na tração de trens e navios, sistemas de ventilação, sistemas
de bombeamento de fluidos também são, hoje em dia, realizados por
conversores eletrônicos. As fontes de alimentação, cada vez mais
eficientes e compactas, também estão presentes no dia-a-dia dos seres
humanos, em seus computadores, tablets, celulares, aparelhos de
televisão, sistemas de iluminação (xênon, led, fluorescentes). Enfim,
independente da profissão, cultura ou idologia, o processamento
eletrônico da energia está presente na vida das pessoas, de uma forma
em geral.
E o que estes sistemas que processam energia nas mais diversas
áreas da indústria, comércio, resisdências e transporte têm em comum?
A necessidade, em maior ou menor grau, de controle de variáveis como
tensão ou corrente, as quais, por sua vez, atuarão diretamente no
processo em questão, seja ele o posicionamento e a velocidade de um
motor ou uma luminosidade de uma lâmpada. Estes sistemas necessitam
de controle em virtude da incerteza existente em realação aos
parâmetros que compõe os conversores, como: os valores de tensão e
corrente de entrada, da carga, bem como dos componentes elétricos
ativos e passivos que são usados na confecção dos conversores. Para que
os conversores estáticos possam desempenhar com excelência o
processamento da energia, independente das variações dos parâmetros
citados, é necessário um projeto adequado deste sistema de controle.
A concepção do projeto de controle de um conversor estático, por
sua vez, depende de diversor fatores:
• O tipo do conversor;
• O modo de operação do conversor;
• A modulação empregada;
Apostila de Controle de Conversores Estáticos
PPGEEL
2
Introdução Geral
•
•
O modelo da carga;
A dinâmica da carga e do conversor.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
2
3
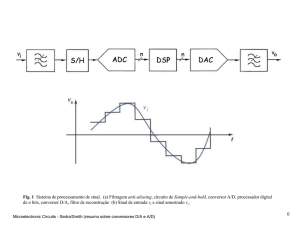
Conceitos de Modulação por Largura de Pulsos[1]
Na maioria das aplicações industriais envolvendo conversores
estáticos a carga a ser acionada é do tipo motriz. Neste tipo de aplicação,
a variação de velocidade no motor a ser acionado é uma característica
muito desejável. Isso é possível controlando a tensão na saída, no caso
de motores cc ou controlando a tensão e a frequência, no caso de
motores ca. Para isso, utilizam-se conversores cc-cc e cc-ca.
Uma técnica largamente aplicada nesses acionamentos é a
modulação por largura de pulso, que consiste na comparação de dois
sinais de tensão, um de baixa frequência (referência) e o outro de alta
frequência (portadora), resultando em um sinal alternado com
frequência fixa e largura de pulso variável.
2.1 Parêmtros da Modulação PWM
A Modulação por Largura de Pulso (Pulse Width Modulation PWM) é comumente composta de parâmetros de circuitos:
• Sinal de Referência;
• Sinal de Portadora;
• Modulador
• Geração de Sinal Complementar
• Tempo Morto
Os quais serão detalhados na sequência.
2.1.1
Sinal de Referência
Para se obter um sinal na saída de um conversor chaveado com a
forma desejada, é necessário modulá-lo em alta freqüência. Este sinal a
ser modulado é chamado sinal de referência, o qual é a imagem da
tensão (ou corrente) de saída buscada.
Nos conversores CC-CC, a referência é um sinal de tensão
contínuo, pois o que se deseja obter é justamente uma tensão contínua
na saída do conversor, conforme Fig. 2.1.
Apostila de Controle de Conversores Estáticos
PPGEEL
4
Conceitos de Modulação por Largura de Pulsos
Fig. 2.1 – Sinal de referência para um conversor CC-CC
Já nos conversores CC-CA o sinal de referência é senoidal, pois o
que se busca na saída é uma tensão alternada. Portanto, se é desejado
uma frequência de 60Hz na saída, deve-se aplicar um sinal de referência
com as mesmas características, conforme Fig. 2.2.
Em conversores CC-CA Trifásicos existe a necessidade de
utilização de três sinais senoidais defasados de 120o.
Fig. 2.2 – Sinal de referência para um conversor CC-CA
Fig. 2.3 - Sinais de referência para um conversor CC-CA Trifásico
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
2.1.2
5
Sinal de Portadora
É um sinal de alta frequência, na ordem de KHz o qual é
responsável pela definição da frequência de comutação e pela razão
cíclica. Este sinal deve possuir uma freqüência no mínimo duas vezes
maior que o sinal de referência (Teorema de Shannon), mas na prática, é
necessário pelo menos 10 vezes para que se tenha uma boa reprodução
do sinal na saída do conversor. Este sinal será responsável pela
frequência de comutação dos interruptores (semicondutores) do circuito
de potência do acionamento.
Em conversores CC-CC, é utilizado um sinal dente-de-serra
como portadora, conforme Fig. 2.3. Já em Conversores CA-CA,
normalmente utiliza-se como portadora um sinal triangular, conforme
Fig. 2.5.
Fig. 2.4 – Sinal dente de serra
Fig. 2.5 – Sinal triangular
Apostila de Controle de Conversores Estáticos
PPGEEL
6
2.1.3
Conceitos de Modulação por Largura de Pulsos
Modulador (Comparador)
É o circuito responsável por comparar o sinal de referência com
a portadora. A largura do pulso na saída do modulador varia de acordo
com a amplitude do sinal de referência em comparação com o sinal
portador. Tem-se assim a modulação por largura de pulso – PWM, do
inglês Pulse Width Modulation.
Na Fig. 2.6 tem-se um exemplo de circuito modulador.
Fig. 2.6 – Geração de Sinal Modulado
As formas de onda nas entradas e saída do comparador, para um
conversor CC-CC, estão demonstradas na Fig. 2.7.
Na Fig. 2.8 podemos ver as formas de onda para um conversor
CC-CA.
Em conversores trifásicos, utilizam se 3 moduladores PWM.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
Vref
7
V2
5
4
3
2
1
0
-1
Vout
0.8
0.4
0
0
0.0002
0.0004
0.0006
Time (s)
Fig. 2.7 - Sinal de referência (Vref), sinal da portadora (V2) e sinal de
saída do modulador (Vout) para um conversor cc-cc.
Fig. 2.8 - Sinal de referência (Vref), sinal da portadora(V2) e sinal de
saída do modulador para um conversor cc-ca.
2.1.4
Geração de sinal complementar
O sinal complementar é necessário quando, por exemplo, existem
dois interruptores (semicondutores) configurados em braço. O
acionamento dos interruptores é feito de maneira inversa, ou seja,
Apostila de Controle de Conversores Estáticos
PPGEEL
8
Conceitos de Modulação por Largura de Pulsos
quando Q1 conduz, Q2 está bloqueado (não está em conduzindo), quando
Q2 conduz, Q1 fica bloqueado e assim sucessivamente.
O sinal complementar consiste em inverter o sinal modulador.
Para isso, pode-se utilizar uma porta lógica inversora (NOT), conforme
Fig. 2.9.
Fig. 2.9 - Obtenção do sinal complementar.
2.1.5
Tempo Morto
Na configuração de interruptores em braço, já apresentada na Fig.
2.9, é necessário assegurar que dois interruptores de um mesmo braço
não sejam acionados ao mesmo tempo, evitando a queima dos mesmos.
Para evitar um efeito de curto-circuito no braço do acionamento, um
tempo morto Tm (Fig. 2.10) deve ser introduzido. O tempo morto é
medido desde o instante em que um semicondutor comuta para seu
estado bloqueado até o instante em que o semicondutor oposto comuta
para o seu estado de condução, garantindo o bom funcionamento e
segurança do acionamento.
Fig. 2.10 - Circuito típico para a obtenção do tempo morto.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
9
O circuito da Fig. 2.10 é composto por portas inversoras,
resistores e capacitores. Através dos pares de resistores e capacitores é
possível ajustar o tempo de descarga dos capacitores, como pode ser
observado nos sinais V1 e V2 na Fig. 2.11. Quanto maior o tempo de
descarga do capacitor, maior o tempo morto gerado pelo circuito. Esta
descarga lenta dos capacitores faz com que as portas inversoras que vem
na sequência demorem a trocar de estado, criando o tempo morto que
pode ser visto em Q1 e Q2. Na prática, para garantir uma operação mais
adequada é comum o emprego de portas inversoras do tipo schmitt
trigger no circuito apresentado.
Vin
0.8
0.4
0
Vin_bar
0.8
0.4
0
V1
0.8
0.4
0
V2
0.8
0.4
0
Q1
0.8
0.4
0
0.001
Q2
0.0015
0.002
Time (s)
0.0025
0.003
Fig. 2.11 –Formas de onda do sinal de comando (Vin), o sinal de
comando complementar(Vin_bar), sinais intermediários (V1 e V2) e os
sinais de comando (Q1) e o complementar (Q2) com o tempo morto.
2.2
Modulações para conversores cc-ca
Nesta seção serão apresentas algumas estratégias de modulação
comumente empregadas em inversores de tensão.
A título de ilustração, salvo informação em contrário, as
modulações apresentadas nesta seção serão testadas em um inversor
monofásico de ponte completa ou no inversor com neutro grampeado
(NPC), conforme apresentado na Fig. 2.12(a) e (b), respectivamente.
Apostila de Controle de Conversores Estáticos
PPGEEL
10
Conceitos de Modulação por Largura de Pulsos
S1
S2
D1
Vi
D3
Carga
S3
S4
D2
D4
(a)
S1
D1
S2
b
+
S3
D2
S4
D4
Dg1
Vi/2
a
-
R
L
iL(t)
Dg2
D3
Vi/2
(b)
Fig. 2.12 - Inversor em ponte completa (a) e inversor com neutro
grampeado (b)
2.2.1
Modulação por largura de pulso único
A modulação por largura de pulso único é uma das formas mais básicas de
se obter os sinais de comando para os interruptores de um inversor, seja ela
do tipo dois ou três níveis. A
Vab
Vi/2
α
α
α
α
ωt
-Vi/2
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
11
Fig. 2.13 mostra o formato da tensão de saída de um Inversor
Três Níveis com Neutro Grampeado. Identifica-se, nesta forma de onda,
a possibilidade de variação do ângulo α. Assim, pode-se desenvolver a
série de Fourier em função deste ângulo.
Vab
Vi/2
α
α
α
α
ωt
-Vi/2
Fig. 2.13 - Forma de onda da tensão de saída do inversor a três níveis
utilizando modulação por largura de pulso único.
Sejam os coeficientes em cosseno da série nulos e os coeficientes
em seno por definição, descritos pela equação (7.1).
T
2
bn = .∫ f (t ).sen(n.ωt )d ωt
T 0
(7.1)
Seja E a metade da tensão de entrada Vi, representada pela
equação (7.2).
E=
Vi
2
(7.2)
Solucionando-se a equação(7.3), tem-se as equações (7.4) e (7.5)
bn =
2π −α
1  π −α
. ∫ E.sen(n.ωt )d ωt + ∫
− E.sen(n.ωt )d ωt 

α
π
α
+


π
(7.3)
bn =
1  E  − cos ( n. ( π − α ) )  E  − cos ( n. ( 2π − α ) )  
 .

 − 
 + cos ( n.(π + α ) )  
π  n  + cos(α .n)
n




(7.4)
Assim, o valor de pico da componente harmônica de ordem n da
forma de onda a três níveis pode ser representado pela equação(7.5)
Apostila de Controle de Conversores Estáticos
PPGEEL
12
bn =
Conceitos de Modulação por Largura de Pulsos
4.E
.cos (α .n )
π.n
(7.5)
A partir da equação (7.6) pode-se calcular a componente
fundamental da tensão de saída do inversor Três Níveis.
b1 =
2.Vi
.cos (α )
π
(7.6)
De acordo com [2], é possível então eliminar ou reduzir uma
componente harmônica com a escolha adequada de um ângulo α. Isto
posto, calcula-se através das equações (7.7) e (7.8) o valor deste ângulo.
 πnbn 
a cos 

 4.E 
α=
n
1, 571
α=
n
(7.7)
(7.8)
onde n = 1,3,…5.
Nota-se que, com a utilização de apenas um ângulo, pode-se
eliminar ou reduzir apenas uma componente harmônica. Como exemplo,
pode-se citar o ângulo α igual a trinta graus, que elimina a harmônica de
ordem três.
A Fig. 2.14 representa a evolução da amplitude das componentes
harmônicas em função da variação do ângulo α; nota-se que não é
possível controlar o valor do termo fundamental e eliminar uma
determinada componente harmônica, utilizando-se apenas um ângulo.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
13
% harmônico em relação a tensão E
150
fundamental
harm.de ordem 3
harm. de ordem 5
harm. de ordem 7
135
120
105
90
%
75
60
45
30
15
0
0
10
20
30
40
50
60
70
80
90
100
α
Fig. 2.14– Harmônicas de tensão em função do ângulo α.
Observa-se, ainda, na Fig. 2.14, que a concentração de
componentes harmônicas de baixa ordem é predominante.
Como o objetivo de minimizar ainda mais o conteúdo harmônico,
algumas soluções são apresentadas na literatura, das quais pode-se citar
a modulação PWM senoidal otimizada e as modulações PWM senoidais
naturais. A primeira propicia um dos melhores resultados em termos de
redução de conteúdo harmônico [2]; prevê o cálculo de n ângulos para
eliminação de n-1 harmônicas, possibilitando, ainda, o controle do valor
da tensão fundamental. Em aplicações práticas, estes ângulos poderiam
ser previamente calculados e armazenados em memórias ou, utilizandose o processamento digital, estes poderiam ser determinados em tempo
real. Já as modulações PWM senoidais naturais são de implementação
simplificada, sendo na sua maioria geradas a partir da comparação entre
formas de onda senoidais e triangulares. Este texto se aterá em descrever
unicamente as modulações PWM senoidais naturais mais difundidas,
também conhecidas como modulações sub-harmônicas.
2.2.2
Modulações PWM senoidais
A modulação PWM senoidal, normalmente, pode ser
inteiramente ou particularmente caracterizada por dois parâmetros,
sejam eles: o índice de modulação e a razão entre as frequências. O
parâmetro índice de modulação, também referenciado em algumas
literaturas como profundidade de modulação, consiste no quociente
entre a amplitude de uma forma de onda moduladora, que normalmente
Apostila de Controle de Conversores Estáticos
PPGEEL
14
Conceitos de Modulação por Largura de Pulsos
é senoidal, e a amplitude de uma forma de onda portadora, normalmente
triangular, conforme mostra a equação (7.9).
Mi =
Am
Ap
(7.9)
Onde:
Am é a amplitude da onda moduladora;
Ap é a amplitude da onda portadora.
A razão entre frequências é o quociente entre a frequência da
forma de onda portadora e a frequência da moduladora, conforme
mostra a equação (7.10).
Mf =
fp
fm
(7.10)
Onde:
fp é frequência da onda portadora triangular;
fm é a frequência da onda moduladora senoidal.
A modulação é dita síncrona quando a razão entre as frequências
Mf é um número inteiro. No modo assíncrono, a frequência da forma de
onda portadora dever ser alta o suficiente a fim de evitar qualquer
perturbação causada por sub-harmônicas [3].
Os três principais métodos de modulação PWM senoidal que
serão abordados neste texto são:
Modulação bipolar, a qual é largamente utilizada em inversores
dois níveis;
Modulação unipolar, que é normalmente empregada em
inversores três níveis;
Modulação dipolar, que pode ser considerada como um caso
particular da modulação unipolar.
2.2.3
Modulação Pwm Senoidal Bipolar
Uma das mais difundidas até então, a modulação Bipolar consiste
basicamente na comparação entre uma forma de onda senoidal e uma
forma de onda triangular, conforme mostra a Fig. 2.15. Entretanto, este
tipo de modulação não é utilizada no inversor Três Níveis, já que se trata
de uma técnica dois níveis.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
Vm
15
Vp
Vab
Fig. 2.15 – Modulação bipolar.
Apenas a título de comparação com as outras técnicas de
modulação, apresenta-se o espectro harmônico da tensão de saída Vab
de um inversor em ponte completa, obtida a partir de simulações
numéricas com tensão entrada de 400 V, índice de modulação Mi = 0,78
e frequência de comutação igual a 20 kHz. Nota-se que as componentes
harmônicas com amplitude significativa são deslocadas para as
proximidades da frequência de comutação.
0,35%
0,30%
0,25%
0,20%
0,15%
0,10%
0,05%
0%
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Ordem da componente harmônica
(a)
Apostila de Controle de Conversores Estáticos
PPGEEL
16
Conceitos de Modulação por Largura de Pulsos
120
110
100
90
80
70
%
60
50
40
30
20
10
0
0
100
200
300
Ordem da componente harmônica
400
500
(b)
Fig. 2.16 – Detalhe do espectro harmônico nas frequências de maior
importância (a), espectro harmônico da tensão de saída completo (b).
2.2.4
Modulação Pwm Senoidal Unipolar
Neste tipo de modulação, os pulsos de comando dos interruptores
podem ser gerados através da comparação entre duas ondas portadoras
triangulares e uma moduladora senoidal. Na referência [4] esta
estratégia é também denominada como método clássico de modulação
três níveis. A Fig. 2.17 apresenta a modulação unipolar na geração do
comando dos interruptores do inversor Três Níveis (S1, S2, S3 e S4).
Nota-se que as formas de onda portadoras triangulares Vp1 e Vp2
encontram-se em fase com a moduladora senoidal Vm, quando esta
passa por zero.
Vm
Vp1
Vp2
S1
S3
S2
S4
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
17
Fig. 2.17 – Modulação PWM Unipolar.
A razão entre frequências Mf pode ser definida pelas equações
(7.11) ou (7.12).
M f = 6.(2.i + 1)
i = 0,1,2,...
(7.11)
M f = 3.(2.i + 1)
i = 0,1,2,...
(7.12)
A Fig. 2.18 mostra o Inversor Três Níveis juntamente com o
circuito de comando utilizado para obter os sinais de acionamento dos
interruptores.
Utilizando-se um simulador numérico [5], obtém-se a forma de
onda da tensão de saída do inversor e a forma de onda da corrente que
circula através da carga. Nesta simulação, a frequência da tensão
moduladora é 60 Hz e a frequência das portadoras triangulares adotada
foi 20 kHz, sincronizadas com a tensão senoidal. O índice de modulação
adotado é o mesmo da simulação anterior, ou seja, igual a 0,78,
enquanto que o valor da frequência de corte da carga RL escolhido foi
de 112 Hz, definido pelos valores do resistor de 4,2 Ω e do indutor de 6
mH; tais parâmetros foram adotados para se obter uma carga com
potência aparente de 10 kVA com tensão de saída 220V. Os
interruptores utilizados na simulação são ideais e a tensão de barramento
Vi é de 800 V.
S1
Dg1
Vi/2
+
S1
S3
D1
Vp1
a
R
L
S2
b
D2
S3
D3
Vm
IL
Dg2
+
-
Vi/2
S4
D4
S2
S4
Vp2
Fig. 2.18 – Inversor com neutro grampeado três níveis e circuito de
comando para modulação unipolar.
A partir da análise harmônica dos resultados de simulação da
tensão de saída do inversor e da corrente através da carga, representados
pela Fig. 2.19, tem-se as taxas de distorção harmônica iguais a 1,52 % e
0,2 % respectivamente, truncados na harmônica de centésima.
Apostila de Controle de Conversores Estáticos
PPGEEL
18
Conceitos de Modulação por Largura de Pulsos
400V
0V
-400V
Tensão Vab
65A
0A
-65A
16.6ms
IL(t)
20.0ms
25.0ms
30.0ms
34.8ms
Fig. 2.19 – Tensão e corrente na carga, modulação unipolar.
O espectro harmônico em detalhe e completo da tensão de saída
Vab do inversor Três Níveis está apresentado na Fig. 2.20.
0,30%
0,25%
0,20%
0,15%
0,10%
0,05%
0%
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Ordem da componente harmônica
(a)
120
110
100
90
80
70
%
60
50
40
30
20
10
0
0
100
200
Ordem da componente harmônica
Apostila de Controle de Conversores Estáticos
300
400
(b)
PPGEEL
Conceitos de Moduilação por Largura de Pulso
19
Fig. 2.20 – Detalhe do espectro harmônico nas frequências de maior
importância (a), espectro harmônico da tensão de saída completo (b).
Observa-se que as harmônicas de baixa ordem, mais difíceis de
serem filtradas não são predominantes, e as harmônicas de maior
amplitude são deslocadas para a frequência de comutação, conforme é
esperado. Comparando-se o espectro harmônico da tensão de saída com
modulação a dois níveis, apresentado na Fig. 2.16, com o obtido para a
modulação três níveis da Fig. 2.20, verifica-se que a amplitude das
harmônicas na frequência de comutação é reduzida pela metade,
diminuindo o esforço de filtragem.
Utilizando-se este mesmo princípio de modulação, entretanto,
empregando duas portadoras triangulares de mesma amplitude e
defasadas em cento e oitenta graus, tem-se a modulação três níveis,
usualmente empregada no comando dos interruptores do inversor em
Ponte Completa. Um detalhe da forma como é gerada este tipo de
modulação está apresentado na Fig. 2.21.
Vm
Vp1
Vp2
S1
S3
S2
S4
Vab
Vi
-Vi
Fig. 2.21 – Modulação três níveis para o inversor em Ponte Completa.
Adotando-se os mesmos parâmetros empregados na simulação
numérica do inversor Três Níveis com neutro grampeado ao inversor em
Ponte Completa da Fig. 2.22, obtém-se o espectro harmônico da tensão
de saída, conforme mostra a Fig. 2.23.
Apostila de Controle de Conversores Estáticos
PPGEEL
20
Conceitos de Modulação por Largura de Pulsos
S1
S2
D1
Vi
D3
Carga
S3
S4
D2
D4
Fig. 2.22 – Inversor em ponte completa.
100
90
80
70
60
%
50
40
30
20
10
0
0
200
400
600
800
Ordem da componente harmônica
Fig. 2.23 – Espectro harmônico da tensão de saída três níveis do
Inversor em Ponte Completa.
Comparando-se os espectros harmônicos das tensões de saída dos
inversores em Ponte Completa e Três Níveis, apresentados nas Fig. 2.20
e Fig. 2.23 respectivamente, percebe-se que a frequência da tensão de
saída do inversor em Ponte Completa é o dobro da frequência de
comutação de seus interruptores. Esta situação também fica evidente na
Fig. 2.21. Desta forma, caso fossem projetados filtros para eliminar as
componentes harmônicas da tensão de saída destes inversores, operando
numa mesma frequência de comutação, seguramente o volume do filtro
do inversor em Ponte Completa seria menor do que o volume do filtro
do inversor Três Níveis com Neutro Grampeado. Ressalta-se entretanto,
que em um trabalho recente [6], utilizando-se dois braços do inversor
Três Níveis e um indutor de circulação, tem-se o dobro da frequência de
comutação na tensão de saída, e esta passa a ter cinco níveis. A principal
desvantagem desta topologia reside na necessidade de se utilizar o dobro
de interruptores.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
2.2.5
21
Modulação PWM Senoidal Por Portadora Com Simetria De
Um Quarto De Onda
Este tipo de modulação também pode ser gerado, comparando-se
duas formas de onda portadoras triangulares com uma moduladora
senoidal, conforme está mostrado na Fig. 2.24, obtendo-se, assim, os
sinais de comando para o inversor Três Níveis. A distinção da geração
deste tipo de modulação, em relação à modulação PWM clássica, é que
as ondas portadoras encontram-se adiantadas em noventa graus da
moduladora quando esta passa por zero.
Vp1
Vm
Vp2
S1
S3
S2
S4
Fig. 2.24 - Modulação Bipolar com simetria de um quarto de onda.
A razão entre frequências Mf deve ser determinada pela equação
(7.13).
Mf = 3.(2.i + 1)
i = 0,1,2,...
(7.13)
Segundo [3], [2] este tipo de modulação possibilita a redução do
conteúdo harmônico em relação à modulação convencional. Com o
intuito de realizar um comparativo, efetua-se a análise harmônica da
tensão de saída do inversor Três Níveis com os mesmos parâmetros
empregados nas modulações anteriores. A taxa de distorção harmônica
calculada até a harmônica de centésima ordem resulta em 0,79 % e a
taxa de distorção da corrente em 0,16 %.
Apostila de Controle de Conversores Estáticos
PPGEEL
22
Conceitos de Modulação por Largura de Pulsos
A Fig. 2.25 apresenta o espectro harmônico da tensão de saída do
inversor, observa-se, em detalhe, que o conteúdo harmônico é reduzido
à medida em que a ordem da harmônica aumenta, de forma mais
acentuada do que na modulação unipolar sem simetria de um quarto de
onda.
120
110
100
0,25%
90
0,20%
80
70
0,15%
%
60
50
0,10%
40
0,05%
30
20
0%
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
Ordem da componente harmônica
33
35
37
39
10
0
0
100
200
Ordem da componente harmônica
300
400
Fig. 2.25 – Análise harmônica da tensão de saída do inversor com
modulação por portadora com simetria de um quarto de onda.
2.2.6
Modulação PWM Senoidal Dipolar
Este processo de modulação pode ser considerado com uma
extensão da modulação bipolar (2 níveis), tanto o nome quanto a
modulação foram propostas por Velaerts et alli [4]. A obtenção dos
pulsos de comando para os interruptores é feita comparando-se uma
onda portadora triangular com duas ondas moduladoras senoidais; ao
passo que, a portadora triangular é simétrica em relação ao eixo das
abscissas, uma das senóides excursiona somente no semiplano positivo
do eixo das ordenadas e a outra somente no semiplano negativo. Esta
comparação, bem como a geração dos pulsos de comandos dos
interruptores está representado pela Fig. 2.26.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
23
Vp
H
Vm2
Vm1
K
S1
S3
S2
S4
Fig. 2.26 – Modulação PWM dipolar.
Observa-se que, quando o parâmetro H for igual ao parâmetro K,
ambos identificados na Fig. 2.26, tem-se a modulação bipolar. O valor
da tensão fundamental para este tipo de modulação é determinado pela
equação (7.14).
V1 = M i .
Vi
.sen(ω.t )
2
(7.14)
O índice de modulação Mi já descrito anteriormente, pode ser
determinado pela equação (7.9).
É importante salientar que, para a modulação dipolar o índice de
modulação fica limitado em 0,5, incorrendo na limitação do valor
máximo da tensão da fundamental. Assim, o valor de pico do termo
fundamental não pode ser superior a um quarto do valor da tensão de
entrada Vi. Esta situação pode ser bem compreendida, observando-se a
Fig. 2.26, onde os interruptores atingem seu valor máximo da razão
cíclica, quando as ondas moduladoras se aproximam do eixo das
abscissas.
A Fig. 2.27 representa o inversor Três Níveis com o respectivo
Apostila de Controle de Conversores Estáticos
PPGEEL
24
Conceitos de Modulação por Largura de Pulsos
circuito de comando para gerar os pulsos de acionamento dos
interruptores, a partir da modulação dipolar. Adotando-se um índice de
modulação de 0,38 e uma frequência de comutação de aproximadamente
20 kHz, simulou-se o circuito em questão.
-
S1
Dg1
Vi/2
S1
S3
D1
+
Vm1
a
R
L
S2
b
D2
S3
D3
Vp
IL
Dg2
S2
S4
+
Vi/2
S4
Vm2
D4
Fig. 2.27 – Inversor Três Níveis e circuito de comando para modulação
dipolar.
Um detalhe da tensão sobre a carga, juntamente com a forma de
onda da corrente são mostrados na Fig. 2.28. Atenta-se ao fato de que
propositadamente as duas formas de onda não estão sincronizadas em
relação ao eixo do tempo, possibilitando assim uma melhor
visualização.
400V
0V
-400V
24.80ms
Tensão Vab
25.00ms
25.20ms
25.40ms
25.60ms
25.80ms
35A
0A
-35A
16.6ms
20.0ms
25.0ms
30.0ms
34.8ms
IL(t)
Fig. 2.28 – Detalhe da tensão Vab e corrente na carga.
A Fig. 2.29 apresenta os resultados da análise harmônica da
tensão e da corrente de saída do inversor Três Níveis utilizando a
modulação dipolar. A taxa de distorção harmônica da tensão é de 2,79 %
e da corrente da carga de 0,338 %; observa-se que os parâmetros da
carga são os mesmos utilizados na modulação PWM unipolar e que o
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
25
cálculo da taxa de distorção é efetuado até a harmônica de centésima
ordem.
200
180
160
0,50%
0,45%
140
0,40%
0,35%
120
0,30%
% 100
0,25%
80
0,20%
0,15%
60
0,10%
0,05%
40
0%
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Ordem da componente harmônica
20
0
0
100
200
300
Ordem da componente harmônica
400
500
Fig. 2.29 – Espectro harmônico da tensão de saída do invesor Três
Níveis com modulação dipolar.
Através dos resultados obtidos a partir das simulações, conclui-se
que a modulação proposta por Velaerts et alli [4] possui algumas
desvantagens em relação à modulação PWM senoidal com simetria de
um quarto de onda. Pode-se citar a limitação do valor da tensão
fundamental e a presença de harmônicas em frequências mais baixas
como sendo fatores importantes na escolha entre uma ou outra estratégia
de modulação.
2.3 Modulação com Três ou Mais Níveis
Nesta seção serão apresentadas estratégias de modulação por
largura de pulso senoidais para conversores com múltiplos níveis de
tensão na carga.
2.3.1
Modulação com Portadoras Dispostas em Fase (Phase
Disposition – PD)
A modulação com portadoras dispostas em fase é uma modulação
onde todos os semicondutores são comutados em alta frequência. Os
sinais de comando são obtidos através da comparação do sinal de
referência com uma das portadoras. Se o sinal de referência é maior que
o da respectiva portadora, o interruptor é mantido conduzindo e, se a o
sinal de referência é inferior ao da portadora, o interruptor permanece
bloqueado. Geralmente são empregadas portadoras triangulares, as quais
são dispostas em fase, com amplitudes iguais, diferindo apenas no seu
valor médio. O número de portadoras necessárias é “ λ − 1 ”, onde “ λ ” é
o número de níveis obtidos na tensão de fase de saída do conversor. Na
Fig. 2.30 é mostrado um exemplo de modulação com as portadoras
dispostas em fase para um conversor com cinco níveis na tensão de fase.
Apostila de Controle de Conversores Estáticos
PPGEEL
26
Conceitos de Modulação por Largura de Pulsos
VRefA
VPort1
VPort2
VPort3
VPort4
Fig. 2.30 – Modulação com as portadoras dispostas em fase (Phase
Disposition – PD).
2.3.2
Modulação com as Portadoras Dispostas em Oposição de
Fase (Phase Opposition Disposition – POD)
A modulação com as portadoras dispostas em oposição de fase,
como o próprio nome sugere, possui as portadoras negativas dispostas
com 180° de defasagem das portadoras positivas, conforme pode ser
conferido na Fig. 2.31.
VRefA
VPort1
VPort2
VPort3
VPort4
Fig. 2.31 – Exemplo de modulação com as portadoras dispostas em
oposição de fase (Phase Opposition Disposition – POD).
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
27
Esta modulação também comuta todos os interruptores em alta
frequência e, assim como a anterior, são necessárias “ λ − 1 ” portadoras
para sua implementação. A principal diferença desta modulação para a
modulação “PD” é em relação à Distorção Harmônica Total (DHT)
presente na tensão de linha dos conversores. Embora as duas
modulações proporcionem aproximadamente a mesma DTH na tensão
de fase, a modulação com as portadoras em fase possibilita um melhor
cancelamento de harmônicas na tensão de linha, proporcionando uma
DTH na tensão de linha mais baixa do que a modulação com as
portadoras em oposição de fase [7].
2.3.3
Modulação com as Portadoras Dispostas em Oposição
Alternada de Fase (Alternative Opposition Disposition –
APOD)
A modulação com as portadoras dispostas em oposição alternada
de fase possui características gerais semelhantes às da modulação
previamente apresentada, porém neste caso, a defasagem de 180° das
portadoras é de uma portadora para a portadora seguinte, e não das
portadoras positivas e negativas como na modulação POD. Uma
amostra da modulação com as portadoras dispostas em oposição de fase
pode ser averiguada na Fig. 2.32.
VRefA
VPort1
VPort2
VPort3
VPort4
Fig. 2.32 – Exemplo de modulação com as portadoras dispostas em
oposição alternada de fase (Alternative Phase Opposition Disposition –
APOD).
Apostila de Controle de Conversores Estáticos
PPGEEL
28
2.3.4
Conceitos de Modulação por Largura de Pulsos
Modulação com as Portadoras com Deslocamento de Fase
(Phase Shifted – PS)
A modulação com as portadoras com deslocamento de fase
emprega “ λ − 1 ” portadoras, todas com a mesma amplitude e nível
médio nulo. As portadoras são deslocadas entre si de 360°
( λ − 1)
. Nesta
modulação os interruptores comutam durante todo tempo, não havendo
intervalos de tempo nos quais os interruptores permanecem mais de um
período bloqueados (ou conduzindo). Esta característica proporciona a
mesma qualidade na tensão de saída que as modulações anteriores, com
resultados semelhantes em termos de DHT. A filtragem da tensão de
saída produzida com esta modulação se torna mais simples, pois as
componentes harmônicas dominantes concentram-se em torno
frequência ( λ − 1) ⋅ f Port , elevando a ordem das componentes harmônicas
na tensão de saída. Em contrapartida o número de comutações é maior,
elevando as perdas. Um exemplo de modulação com as portadoras com
deslocamento de fase é visualizado na Fig. 2.33.
VRefA
VPort1
VPort2
VPort3
VPort4
Fig. 2.33 – Exemplo de modulação com as portadoras com
deslocamento de fase (Phase Shifted – PS).
Esta modulação apresenta ainda, tipicamente, uma distribuição de
perdas equilibrada entre os semicondutores de potência. Esta
característica é de grande importância para o projeto dos sistemas de
refrigeração (que pode ser natural, com ventilação forçada ou com
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
29
circulação de fluidos), que são necessários para a dissipação do calor
gerado na condução e na comutação dos interruptores.
2.3.5
Comparação Entre as Modulações
Para comparar as modulações apresentadas foram realizadas
algumas simulações numéricas com o programa de simulação PSIM.
Adotou-se o conversor multinível simétrico empregando cascata de
conversores em ponte completa, conforme a, com a associação de dois
conversores em cascata, possibilitando sintetizar cinco níveis na tensão
de fase e nove níveis na tensão de linha.
Apostila de Controle de Conversores Estáticos
PPGEEL
Fig. 2.34 - Inversor trifásico de " λ "níveis empregando cascata de
células monofásicas de conversores em ponte completa.
Apostila de Controle de Conversores Estáticos
Vx
Vx
Vx
+
+
+
S N 1A'
S N 1A
S N-1 1 A'
D N 1A'
D N 1A
S N 2A'
S N 2A
D N-1 1 A' S N-1 2 A'
D N-1 1 A S N-1 2 A
S N-1 1 A
S 1 2 A'
D N1A'
D1 1 A
S 1 2A
S 1 1 A'
S 1 1A
D N 2 A'
DN 2A
D N-1 2 A'
D N-1 2 A
D 1 2 A'
D1 2 A
A
iA
Vx
Vx
Vx
+
+
+
S N 1B'
S N 1B
S N-1 1 B'
S N-1 1 B
S 1 1 B'
S 1 1B
S 1 2 B'
D N 1B'
D N 1B
S N 2 B'
S N 2B
D N-1 1 B' S N-1 2 B'
D N-1 1 B S N-1 2 B
D N1B'
D1 1 B
S 1 2B
D N 2 B'
DN 2B
D N-1 2 B'
D N-1 2 B
D 1 2 B'
D1 2 B
B
iB
Vx
Vx
Vx
+
+
+
S N 1 C'
S N 1C
S N-1 1 C'
S N-1 1 C
S 1 1 C'
S1 1C
S 1 2 C'
D N 1 C'
DN 1C
S N 2C'
S N 2C
D N-1 1 C' S N-1 2 C'
D N-1 1 C S N-1 2 C
D N1C'
D1 1 C
S1 2C
D N 2C'
D N 2C
D N-1 2 C'
D N-1 2 C
D 1 2 C'
D1 2 C
C
iC
30
Conceitos de Modulação por Largura de Pulsos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
31
As figuras de mérito escolhidas para a comparação entre as
modulações são:
• Distorção Harmônica Total das tensões de fase e de linha – A
distorção harmônica representa o quanto uma forma de onda
possui de componentes harmônicas. Quanto maior for o valor
da DHT mais harmônicas estão presentes e mais distante do
formato sinusoidal é a forma de onda analisada. Este
parâmetro é relevante, pois grande parte dos trabalhos
científicos sobre conversores multiníveis emprega a DHT
como índice para comparações;
• Distorção Harmônica Total de Primeira Ordem (Weighted
Total Harmonic Distortion – WTHD) da tensão de fase e de
linha – A distorção harmônica total de primeira ordem
contempla em seu cálculo a amplitude de cada harmônica e a
ordem da harmônica, onde as harmônicas de ordem mais
elevada têm menor impacto no resultado do cálculo. Esta
figura de mérito é importante nos conversores multiníveis,
pois apresenta uma correlação com a distorção harmônica de
corrente em um motor e, a dificuldade de realizar uma
filtragem de primeira ordem de um determinado sinal [8].
• Perdas de Comutação Normalizada – As modulações sob
análise possuem características diferentes em relação à
comutação dos interruptores. Sendo assim, realizou-se o
cálculo das perdas de comutação nos interruptores
controlados e nos diodos para cada uma das modulações.
As definições de Distorção Harmônica Total (DHT) e Distorção
Harmônica Total de Primeira Ordem (WTHD) são apresentadas em [8].
2
∞
 2 ⋅ V0 
 Vn 
DHT = 
 + ∑ 
 V1  n = 2  V1 
2
(7.15)
e
∞
WTHD =
 Vn 
∑  n 
2
n=2
(7.16)
V1
onde,
n
V0
representa a ordem da harmônica;
representa o nível médio presente na tensão ca;
Apostila de Controle de Conversores Estáticos
PPGEEL
32
Conceitos de Modulação por Largura de Pulsos
representa a amplitude da componente harmônica de
tensão de ordem n = 1, 2,..., ∞ .
Para a confecção da Tabela 2.1 foram realizadas várias
simulações com as seguintes condições:
f o = 50 Hz
frequência fundamental de saída;
f C = 750 Hz
frequência de comutação para análise das
DHT’s;
f C = 20 kHz
frequência de comutação para análise de
perdas;
ma = 0,8 índice de modulação de amplitude;
Vn
A escolha dos parâmetros das condições de operação do
conversor visou à reprodução dos resultados obtidos em [7]. Isto
esclarece porque nesta análise é empregada uma frequência diferente do
restante do trabalho. Salienta-se que, embora os valores de distorção
harmônica não tenham sido idênticos aos valores obtidos pelos autores
do artigo base, estas diferenças não interferem nas conclusões. A
escolha da frequência de comutação de 20 kHz para o cálculo de perdas
foi pautada pela capacidade do interruptor empregado para tal análise, o
SKM 75GB063D. Porém, como os resultados foram parametrizados em
função das perdas obtidas com a modulação PD, alterações na
frequência de comutação não alteram os resultados.
Analisando os resultados da Tabela 2.1 pode-se verificar que
todas as modulações possuem aproximadamente o mesmo conteúdo
harmônico na tensão de fase, diferindo apenas na frequência onde estão
concentradas as componentes harmônicas mais relevantes. Este fato fica
evidente na DHT das tensões de linha, onde o cancelamento de
harmônicas favorece a modulação PD, pois esta modulação concentra as
maiores componentes em frequências nas quais ocorre o cancelamento
quando uma fase é subtraída da outra. Quando a análise da distorção
harmônica leva em consideração a ordem da componente harmônica
(WTHD), atribuindo menor peso às harmônicas de maior ordem, a
modulação PS se apresenta com excelente desempenho. Na modulação
PS a frequência das harmônicas mais relevantes depende da frequência
de comutação e também do número de níveis do conversor, portanto
quanto maior o número de níveis do conversor maior a ordem das
harmônicas. As perdas de comutação proporcionadas pelas modulações
com portadoras defasadas pelo seu nível médio (PD, POD, APOD) são
aproximadamente iguais. A modulação PS, devido ao número de
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
33
comutações mais elevado, apresenta maiores perdas do que as outras
opções de modulação.
Tabela 2.1 – Comparação das distorções harmônicas e das perdas de
comutação entre as modulações PD, POD, APOD e PS para um
inversor trifásico em cascata com cinco níveis.
ma = 0,8
f C = 750 Hz
DHT Fase [%]
DHT Linha [%]
WTHD Fase [%]
WTHD Linha [%]
Perdas de Comutação
Normalizada [%]
f C = 20 kHz
2.3.6
PD
37,949
21,552
2,518
1,452
POD
37,946
35,231
2,436
2,378
APOD
37,948
29,187
2,332
1,786
OS
38,183
29,512
0,543
0,414
100,00
100,32
99,91
405,09
Exemplo de Modulação Híbrida
Outras formas de modulação podem ser encontradas na literatura,
como a modulação híbrida proposta por Zaragoza, J.; Pou, J.; Ceballos,
S. et al. [9] para o conversor com grampeamento através de diodos com
três níveis na tensão de fase. Neste trabalho, os autores propõem uma
modulação baseada em outras duas modulações, onde é utilizado um
sistema de controle para determinar o intervalo de tempo que cada
modulação é utilizada. Esta modulação híbrida foi comparada com as
modulações que a originaram e, como era de se esperar, seu
desempenho é intermediário em relação às modulações originárias.
As duas modulações que compõem a modulação híbrida proposta
são do tipo PWM com portadoras dispostas em fase. A modulação
denominada “modulação PWM senoidal padrão” (Standard Sinusoidal
Pulsewidth Modulation – SPWM) é semelhante à apresentada na seção
2.3.1, porém a referência é modificada pela injeção de componente de
sequência zero. A injeção de componentes de sequência zero na
referência redistribui o tempo de condução dos interruptores, reduz a
ondulação de tensão no ponto central dos capacitores e permite elevar o
índice de modulação do conversor em 15 % [8, 9]. A injeção de
sequência zero na referencia é realizada empregando a equação (7.17)
v 'a = va − v0

 v 'b = vb − v0
v ' = v − v
 c
c
0
Apostila de Controle de Conversores Estáticos
(7.17)
PPGEEL
34
Conceitos de Modulação por Largura de Pulsos
onde:
v0 =
max ( va , vb , vc ) + min ( va , vb , vc )
2
(7.18)
e,
va = ma ⋅ cos ( 2 ⋅ π ⋅ f o )

v = m ⋅ cos 2 ⋅ π ⋅ f − 2 ⋅ π
a
o
 b
3

vc = ma ⋅ cos 2 ⋅ π ⋅ f o + 2 ⋅ π 3
(
(
(7.19)
)
)
onde, f o é a frequência fundamental do sinal de saída e ma é o índice
de modulação de amplitude.
Sendo assim, a modulação SPWM empregada na modulação
híbrida proposta em [9] pode ser visualizada na Fig. 2.35.
A segunda modulação é composta de dois sinais de referência,
um positivo e um negativo, os quais são originados através da expressão
(7.20) [10].

vi − min ( va , vb , vc )
 vip =

2
onde i = {a, b, c}

v
−
max
va , vb , vc )
(
v = i
 in
2
(7.20)
v’a
1
VPort1
0
VPort2
-1
Fig. 2.35 – “Modulação PWM senoidal padrão” (Standard Sinusoidal
Pulsewidth Modulation – SPWM) com injeção de componentes de
sequência zero.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
35
A modulação PWM com dupla referência para cada fase
(Double-Signal Pulsewidth Modulation – DSPWM) pode ser observada
na Fig. 2.36.
v ap
1
VPort1
0
VPort2
-1
v an
Fig. 2.36 – “Modulação PWM com dupla referência” (Double-Signal
Pulsewidth Modulation – DSPWM).
A análise das três modulações em termos da Distorção
Harmônica Total, das perdas por comutação e da ondulação de tensão no
ponto central do barramento de corrente contínua estão sumarizadas na
Tabela 2.2.
Tabela 2.2 – Comparação entre as modulações SPWM e DSPWM
Modulação
DHT
SPWM
DSPWM
HPWM
Menor
Maior
Intermediária
Perda de
Comutação
Menor
Maior
Intermediária
Ondulação de Tensão
no Ponto Central
Maior
Menor
Intermediária
A modulação híbrida proposta em [9] (Hybrid Pulsewidth
Modulation – HPWM) é mostrada na Fig. 2.37.
Pode-se verificar que a modulação híbrida possui duas referências
para cada fase, sendo uma positiva “ vahp ” e uma negativa “ vahn ”. O
intervalo representado pelo ângulo “ δ ” é determinado por um
controlador, visando manter a ondulação de tensão no ponto central do
barramento dentro de um limite imposto pelo projetista, com a menor
perda possível e com a menor DHT. Quando o parâmetro “ δ ” é nulo, a
Apostila de Controle de Conversores Estáticos
PPGEEL
36
Conceitos de Modulação por Largura de Pulsos
modulação híbrida se torna igual à DSPWM e, quando o ângulo “ δ ” é
máximo, a modulação híbrida é igual à SPWM.
vahp
1
HPWM
0
SPWM
-1
δ
δ
δ vahn δ
Fig. 2.37 – Modulação híbrida proposta por Zaragoza (Hybrid
Pulsewidth Modulation – HPWM).
O conversor em cascata empregando células em ponte completa
pode ser encontrado na literatura com outras modulações híbridas. Uma
das mais conhecidas é a que utiliza frequências distintas para cada célula
em cascata [11-14]. Um exemplo desta modulação pode ser averiguado
na Fig. 2.38.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
37
(a)
1
VPort1
0
-1
(b)
VPort2
Fig. 2.38 – Exemplo de modulação híbrida empregando frequências
distintas para cada célula de conversor em ponte completa. (a) Tensão
de saída sintetizada por um dos inversores. (b) Sinal de referência e
portadoras empregadas para determinar os pulsos de comando do
segundo inversor.
Neste tipo de modulação, um conversor ponte completa comuta
em baixa frequência, sintetizando na saída uma onda retangular
conforme a apresentada na Fig. 2.38 (a). Enquanto isso, outro conversor
em ponte completa recebe a modulação PWM mostrada na Fig. 2.38 (b),
para sintetizar a tensão que não foi sintetizada pela célula que comuta
em baixa frequência. Quando se realiza a associação em cascata destes
dois conversores, é obtida na saída uma onda senoidal PWM. Esta
metodologia pode ser aplicada com mais do que duas células em
cascata, bem como com mais de duas frequências de comutação.
2.4
xxxx
2.5
Modulação SHE
Modulação por Vetores Espaciais
xxxx
Apostila de Controle de Conversores Estáticos
PPGEEL
38
2.6
Conceitos de Modulação por Largura de Pulsos
Conclusão
Foram apresentadas e comparadas qualitativamente as principais
técnicas de modulação aplicáveis ao inversor Três Níveis. Das técnicas
de modulação PWM naturais, a modulação com simetria de um quarto
de onda apresentou os melhores resultados no que tange a taxa de
distorção harmônica. Os cálculos efetuados para determinar a taxa de
distorção harmônica levaram em consideração apenas as harmônicas
presentes até a centésima ordem, pois considera-se que, em aplicações
práticas, as harmônicas de alta frequência podem ser filtradas
facilmente, se necessário. A técnica de modulação três níveis, adotada
para comandar o inversor em Ponte Completa, não é aplicável ao
inversor Três Níveis; logo, a frequência de comutação vista pela carga
do inversor Três Níveis é a própria frequência de comutação. A
modulação dipolar apresenta como principal desvantagem a limitação do
índice de modulação, restringindo, desta forma, o valor de pico da
tensão de saída do inversor a um quarto da tensão de barramento. Do
ponto de vista dos cargas trifásicas, a tensão de linha da modulação três
níveis unipolar possuirá cinco níveis, já, a modulação dipolar apresenta
somente três patamares de tensão sobre a carga.
Deve-se salientar que foram exploradas apenas as modulações
PWM senoidais ditas naturais, as quais podem ter seu princípio de
funcionamento digitalizado e otimizado no que se refere à taxa de
distorção harmônica total. Ao longo dos próximos capítulos, optou-se
por adotar a modulação por portadora com simetria de um quarto de
onda, devido aos resultados propiciados pelo método.
Apostila de Controle de Conversores Estáticos
PPGEEL
Conceitos de Moduilação por Largura de Pulso
Apostila de Controle de Conversores Estáticos
39
PPGEEL
40
Revisão dos Conceitos Básicos de Controle
3
3.2.1
Revisão dos Conceitos Básicos de Controle
3.1
Ações básicas dos controladores P, I, PI, PID
3.2
Conceito de pólo, zero, estabilidade
Diagrama de bode
[15] [16] [17] [18] [19]
3.2.1.1
Introdução
O uso de diagramas de Bode na análise da resposta em frequência
de sistemas lineares foi desenvolvido por H.W. Bode e introduzido em
1940 no estudo das características em frequência de amplificadores
eletrônicos. A técnica desenvolvida por Bode foi, posteriormente,
largamente disseminada para análise e projeto de sistemas de controle.
Em linhas gerais, diagramas de Bode possibilitam uma aproximação
efetiva da resposta em frequência de sistemas complexos pela
combinação da resposta de fatores de primeira e segunda ordem.
Embora atualmente os engenheiros responsáveis pelo
desenvolvimento de projetos de sistemas de controle tenham a sua
disposição poderosas ferramentas computacionais que diminuem
sobremaneira a necessidade do traçado manual dos gráficos de módulo e
fase que compõe os diagramas de Bode, tal técnica ainda é bastante
utilizada pela sua facilidade, rapidez e quantidade de informações que se
pode obter de um dado sistema sob análise de forma bastante
simplificada.
3.2.1.1.1 Teoria sobre Diagramas de Bode
O método proposto por Bode é constituído por dois gráficos. O
primeiro gráfico, relacionado a magnitude da função de transferência
G ( jω ) é traçado em função da frequência em escala log-log. O
segundo gráfico, relacionado a fase de G ( jω ) , também é traçado em
função da frequência, porém em escala linear-log. Esta estratégia
permite-nos traçar diagramas de resposta em frequência sistemas de
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
41
ordem elevada, adicionando-se separadamente os gráficos relativos a
cada um termos de primeira e segunda ordem que compõe G ( jω ) .
Como exemplo, consideremos a seguinte função de transferência:
G1 ( s ) =
(s + z )
( s + p)
(8.1)
Admitindo s= jω , pode-se rescrever (8.1) na seguinte forma:
G1 ( s ) = G1 ( jω ) + cos φ1 + j G1 ( jω ) sin φ1
(8.2)
Com a magnitude dada por:
(z2 + ω2 )
G1 ( jω ) =
(8.3)
( p2 + ω 2 )
E com a fase dada por:
φ1 = arctan
ω
z
− arctan
ω
(8.4)
p
No caso geral de uma função de transferência com “n” pólos e
“m” zeros, o módulo será calculado de acordo com (4), isto é:
G ( jω ) = K
∏
∏
m
i =1
n
j =1
( zi ) 2 + ω 2
(8.5)
( p j )2 + ω 2
Sendo a fase, dada pela diferença das somatórias das
contribuições de fase cada um dos “m” zeros e “n” pólos da G ( jω ) , ou
seja:
φ (G ( jω )) = ∑ i =1 arctan
m
ω
zi
− ∑ i =1 arctan
n
ω
pi
Apostila de Controle de Conversores Estáticos
(8.6)
PPGEEL
42
Revisão dos Conceitos Básicos de Controle
Pela análise da equação (8.5) é direto concluir-se a seguinte
relação:
log G ( jω ) = log K + ∑ i =1 log ( zi ) 2 + ω 2 −∑ j =1 log ( pi ) 2 + ω 2
m
n
(8.7)
Justificando-se a idéia de representar o gráfico de magnitude de
G ( jω ) em escala log-log. Através das equações (8.6) e (8.7) pode-se
então concluir que a resposta em frequência completa de uma função de
transferência genérica G ( jω ) pode ser obtida através da somatória da
resposta em frequência de cada dos fatores que a compõe.
3.2.1.2
Composição do Diagrama de Bode
Quando se trata de uma função de transferência com vários pólos
e zeros, o traçado das curvas de magnitude e de fase, que compõe o
diagrama de Bode, é realizado pela combinação das curvas de
magnitude e fase de cada um dos termos que a compõe. Desta forma, a
declividade das assíntotas da curva de magnitude da função de
transferência é dada pela somatória das declividades das assíntotas para
cada um dos termos individuais. Portanto na composição da curva
assintótica de magnitude as declividades mudam nas frequências em que
existem pontos de quebra: +20 dB/década se o ponto de quebra for
relativo a um termo de primeira ordem do numerador, -20 dB/década se
for relativo a um termo de primeira ordem no denominador e, ±40
dB/década se o ponto de quebra for associado a um termo de segunda
ordem no numerador ou no denominador respectivamente. Para baixas
frequências, as assíntotas são determinadas pelo valor de γ dos termos
k0ω γ , determinando-se k0 na frequência ω=1.0 rad/s. Desta forma, o
traçado completo da curva de magnitude do diagrama de Bode é
realizado começando-se pelo traçado das assíntotas em baixas
frequências, alterando-se as declividades sequencialmente a cada ponto
de quebra de forma a cobrir toda a faixa de frequências de interesse.
A composição do diagrama de Bode de fase é feita adicionandose as curvas individuais de fase. Uma forma rápida bastante utilizada
para o traçado da curva assintótica de fase consiste em cada um dos
o
termos de primeira ordem no numerador adicionar-se +90 na frequência
o
em que existe ponto de quebra e, da mesma forma, adicionar-se –90 se
os termos de primeira ordem estiverem no denominador. Se o ponto de
quebra relacionar-se com fatores de segunda ordem, descrito
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
43
anteriormente como sendo a terceira classe de termos, os incrementos de
fase serão de ±180º se o ponto de quebra for associado a um termo de
segunda ordem no numerador ou no denominador respectivamente.
Uma vez obtidas as curvas assintóticas de magnitude e fase,
refina-se o traçado das mesmas empregando as regras de transição
apresentadas anteriormente.
No intuito de abstrair os conceitos descritos até o momento,
abaixo, segue alguns exemplos de gráficos de bode, para diferentes
funções de transferência. Posteriormente, será descrito o procedimento,
passo a passo, para montagem dos destas curvas.
a) Exemplo de diagrama de bode para uma função de
transferência que contenha zeros e pólos reais:
G (s) =
2000( s + 0.5)
[ s ⋅ ( s + 10) ⋅ ( s + 50)]
Bode Diagram
40
30
20
Magnitude (dB)
10
0
-10
-20
-30
-40
-50
-60
0
Phase (deg)
-45
-90
-135
-180
10
-1
0
1
10
10
2
10
Frequency (Hz)
Fig. 3.1 - Diagrama de Bode: Função de transferência com zeros e pólos
reais
b) Exemplo de diagrama de bode para uma função de
transferência que contenha pólos reais e complexos:
G (s) =
10
[ s ⋅ ( s + 0.4 s + 4)]
2
Apostila de Controle de Conversores Estáticos
PPGEEL
44
Revisão dos Conceitos Básicos de Controle
Bode Diagram
40
30
20
Magnitude (dB)
10
0
-10
-20
-30
-40
-90
Phase (deg)
-135
-180
-225
-270
10
-1
10
0
Frequency (Hz)
Fig. 3.2 - Diagrama de Bode: Função de transferências com pólos reais
e complexos
c) Exemplo de diagrama de bode para uma função de
transferência que contenha zeros e pólos, reais e complexos:
G (s) =
0.01( s 2 + 0.01s + 1)
[ s ⋅ (( s 2 / 4) + 0.02( s / 2) + 1)]
2
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
45
Bode Diagram
0
-10
-20
Magnitude (dB)
-30
-40
-50
-60
-70
-80
0
Phase (deg)
-45
-90
-135
-180
-1
10
10
0
Frequency (Hz)
Fig. 3.3 - Diagrama de Bode: Função de transferência com zeros e pólos
reais e complexos.
3.2.1.3
Construção do Diagrama de Bode
O procedimento empregado para construção do diagrama de bode
pode ser resumido em oito passos descritos a seguir.
Passo 1: Considera-se a seguinte função de transferência a qual
deseja-se obter o Diagrama de Bode:
G (s) = K ⋅
s m + a1 s m −1 + ... + am −1 s + am
s n + b1 s n −1 + ... + bm −1 s + bm
(8.8)
Onde: m ≤ n
A função de transferência (8.8) deve ser manipulada de forma a
aparecer as três classes de termos possíveis encontrados na sua
composição, por exemplo:
2
 jω 
z  jω 
∏ i =1 ( jω r1 + 1)∏ i =c/21  ω  + 2ξi  ω  + 1
 i 
 i 
G ( jω ) = K o ( jω )γ
(8.9)
2
 jω 
pR
pc /2  jω 
∏ k =1 ( jωτ k + 1)∏ k =1  ω  + 2ξ k  ω  + 1
 i 
 k 
Apostila de Controle de Conversores Estáticos
PPGEEL
zR
46
Revisão dos Conceitos Básicos de Controle
Portanto, “γ” zeros ou pólos na origem que representam a
primeira classe termos previamente apresentadas, “zR” zeros ou “pR”
pólos reais representando a segunda classe de termos e “zc/2” pares de
zeros ou “pc/2” pares de pólos complexos conjugados que representam a
terceira e última classe de termos.
Passo 2: Determinar o valor de γ para classe de termos K o ( jω )γ .
Traçar a assíntota de baixa frequência a partir do ponto Ko determinado
na frequência ω=1 rad/s. A assíntota terá declividade de 20γ dB/década.
Passo 3: Estender a assíntota de baixa frequência até o primeiro
ponto de quebra. Neste ponto, alterar a declividade da curva assintótica
de ±20 dB/década ou ±40 dB/década dependendo se o ponto de quebra
está associado a um termo de primeira ou segunda ordem no numerador
ou denominador da função de transferência. Este procedimento deve ser
repetido em toda faixa de frequências até que seja alcançado o último
ponto de quebra.
Passo 4: Com base na curva assintótica de magnitude
incrementa-la nos pontos de quebra associados a termos de primeira de
+3 dB, se for um termo do numerador, e –3 dB se for do denominador.
Se o ponto de quebra for associado a termos de segunda ordem,
representar os vales ou picos empregando a relação G ( jω ) = 2ξ ,ou
G ( jω ) = 1 / 2ξ , no ponto de quebra.
Passo 5: Traçar a curva assintótica de fase para baixas
frequências, isto é,
φ = γ x90°
Passo 6: Da mesma forma que na curva de magnitude, estender a
assíntota de baixa frequência até o primeiro ponto de quebra, alterando a
fase em ±90º ou ±180º. Se o ponto de quebra estiver relacionado a
termos de primeira ordem no numerador, a curva assintótica de fase será
alterada em +90º, por outro lado, se estiver relacionado ao denominador,
a curva assintótica de fase será alterada em –90º. Para termos de
segunda ordem a alteração da curva assintótica de fase sofrerá uma
alteração de ±180º.
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
47
Passo 7: Traçar nas curvas assintóticas de fase individuais as
transições para os termos de primeira e de segunda ordem.
Passo 8: Adicionar graficamente cada uma das curvas
individuais, começando pela assíntota de baixa frequência e finalizando
pela assíntota de alta frequência. Quanto mais distantes estiverem os
pontos de quebra sucessivos, mais próximas as curvas de magnitude e
fase assintóticas serão das curvas reais.
A seguir, são mostradas as curvas assintóticas de magnitude e
fase associadas a cada uma das classes de termos básicos que compõe as
funções de transferência.
1- Função Transferência caracterizada por Ganho: G ( jω ) = K
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
a)
Fase G(jw) em graus
Exemplo do diagrama de Bode com traçado real:
G ( s ) = 10
Apostila de Controle de Conversores Estáticos
PPGEEL
48
Revisão dos Conceitos Básicos de Controle
Bode Diagram
21
Magnitude (dB)
20.5
20
19.5
19
1
Phase (deg)
0.5
0
-0.5
-1
10
-1
10
0
10
1
Frequency (Hz)
Fig. 3.4 - Diagrama de Bode: Função transferência caracterizada por
Ganho

jω 
2- Função Transferência caracterizada por Zero: G ( jω ) = 1 +

ω

1 
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
a)
Fase G(jw) em graus
Exemplo do diagrama de Bode com traçado real:
G( s) = s + 1
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
49
Bode Diagram
25
Magnitude (dB)
20
15
10
5
0
Phase (deg)
90
45
0
10
-1
10
0
Frequency (Hz)
Fig. 3.5 - Diagrama de Bode: Função Transferência caracterizada por
Zero
3- Função Transferência caracterizada por Pólo:

jω 
G ( jω ) = 1 +

 ω1 
−1
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
Fase G(jw) em graus
a) Exemplo do diagrama de Bode com traçado real:
Apostila de Controle de Conversores Estáticos
PPGEEL
50
Revisão dos Conceitos Básicos de Controle
G (s) =
1
( s + 1)
Bode Diagram
0
Magnitude (dB)
-5
-10
-15
-20
-25
Phase (deg)
0
-45
-90
10
-1
10
0
Frequency (Hz)
Fig. 3.6 - Diagrama de Bode: Função transferência caracterizada por
Pólo
4- Função Transferência caracterizada por Zero na origem: G ( jω ) = jω
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
Fase G(jw) em graus
b) Exemplo do diagrama de Bode com traçado real:
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
51
G (s) = s
Bode Diagram
40
Magnitude (dB)
30
20
10
0
-10
-20
91
Phase (deg)
90.5
90
89.5
89
10
-1
10
0
10
1
Frequency (Hz)
Fig. 3.7 - Diagrama de Bode: Função transferência caracterizada por
Zero na origem
5- Função Transferência caracterizada por Pólo na origem:
 1 
G ( jω ) = 

 jω 
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
Apostila de Controle de Conversores Estáticos
Fase G(jw) em graus
PPGEEL
52
Revisão dos Conceitos Básicos de Controle
c) Exemplo do diagrama de Bode com traçado real:
G (s) =
1
s
Bode Diagram
20
Magnitude (dB)
10
0
-10
-20
-30
-40
-89
Phase (deg)
-89.5
-90
-90.5
-91
10
-1
10
0
10
1
Frequency (Hz)
Fig. 3.8 - Diagrama de Bode: Função transferência caracterizada por
Pólo na origem
6- FT com Zeros Complexos:
2
 jω 
 jω 
G ( jω ) = 
 + 2ξ ⋅ 
 + 1 , sendo 0.1 ≤ ξ ≤ 1
 ωn 
 ωn 
Diagrama de Bode Assintótico
Magnitude 20.log.|G(jw)| em dB
Apostila de Controle de Conversores Estáticos
Fase G(jw) em graus
PGEEL
Revisão dos Conceitos Básicos de Controle
53
d) Exemplo do diagrama de Bode com traçado real:
G (s) = s 2 + s + 1
Bode Diagram
40
Magnitude (dB)
30
20
10
0
-10
180
Phase (deg)
135
90
45
0
10
-1
10
0
Frequency (Hz)
Fig. 3.9 - Diagrama de Bode: FT com Zeros Complexos
7- FT - Pólos Complexos:
  jω  2
 jω  
G ( jω ) =  
 + 2ξ ⋅ 
 + 1
  ωn 
ωn  



−1
, sendo 0.1 ≤ ξ ≤ 1
Diagrama de Bode Assintótico
Apostila de Controle de Conversores Estáticos
PPGEEL
54
Revisão dos Conceitos Básicos de Controle
Magnitude 20.log.|G(jw)| em dB
Fase G(jw) em graus
g) Exemplo do diagrama de Bode com traçado real:
1
( s + s + 1)
G (s) =
2
Bode Diagram
10
Magnitude (dB)
0
-10
-20
-30
-40
0
Phase (deg)
-45
-90
-135
-180
10
-1
10
0
Frequency (Hz)
Fig. 3.10 - Diagrama de Bode: Função transferência com Pólos
Complexos
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
3.2.1.4
55
Diferença entre diagrama de Bode real e a aproximação
assintótica
Conforme visto no item anterior, ao construir um gráfico de bode
de uma função transferência por meio de curvas assintóticas, haverá
uma pequena diferença com a resposta real do diagrama de bode. Essa
diferença fica um pouco mais saliente nas chamadas frequência de
“canto” ou de “corte”, onde há uma mudança na inclinação da reta. Em
alguns casos, é interessante conhecer o valor desta diferença, e por isso,
a seguir, será utilizado um exemplo para descrever o procedimento de
cálculo.
Seja a função de transferência:
G (s) =
1
(Ts + 1)
(8.10)
Onde T=0.5, e o pólo =2.
Para esta função, comparando o gráfico assintótico e o real, temse:
Fig. 3.11 - Comparação Diagrama de Bode: Traçado Assintótico x Real
Analisando a Fig. 3.11, percebe-se que a diferença entre as curvas
ocorre em pontos específicos, onde há influência de pólos ou zeros.
Abaixo será descrito como calcular essa diferença nos pontos em
questão:
Apostila de Controle de Conversores Estáticos
PPGEEL
56
Revisão dos Conceitos Básicos de Controle
Ponto 1: ω =
1
:
T
G ( s ) dB = −20 log ((Ts)2 + 1) = −20 log 2 = −3dB arg G ( jω ) = − arg(1 + j ) = −45°
Ponto 2: ω =
1
:
10T
j 

arg G ( jω ) = − arg  1 +  = −5.71°
10


Ponto 3: ω =
10
:
T
arg G ( jω ) = − arg (1 + 10 j ) = −90° + 5.71°
Conforme visto, realmente há uma diferença entre os traçados
assintótico e real do diagrama de bode. Porém, a metodologia utilizada
para o traçado assintótico ainda é uma boa estratégia para estimar o
comportamento de uma função de transferência sem a utilização de
programas e recursos computacionais.
3.2.1.5
Sistemas Lineares de Fase Não Mínima
A definição de sistemas lineares de fase não mínima está
associada diretamente com o posicionamento dos pólos e zeros finitos
da função de transferência do sistema em questão. Funções de
transferência que apresentam todos os seus pólos e zeros localizados no
semiplano esquerdo do plano s são denominadas funções de
transferência de fase mínima. Em contrapartida, se na função de
transferência em questão existir pelo menos um pólo ou zero no
semiplano direito do plano s, o sistema será denominado de fase não
mínima. De forma a justificar tal denominação, considera-se dois
sistemas lineares de primeira ordem descritos pelas funções de
transferência (8.11) e (8.12), apresentadas a seguir:
G1 ( s ) =
( s + 1)
( s + 10)
Apostila de Controle de Conversores Estáticos
(8.11)
PGEEL
Revisão dos Conceitos Básicos de Controle
G2 ( s ) =
( s − 1)
( s + 10)
57
(8.12)
A Fig. 3.12 apresenta os diagramas de pólos e zeros das funções
de transferência (8.11) e (8.12).
Fig. 3.12 - (a) Diagrama de pólos e zeros da função de transferência
(3.10); (b) Diagrama de pólos e zeros da função de transferência (3.11)
Pela análise da Figura 12 (item (a) e (b)) pode-se constatar que
|G1(jω)|=|G2(jω)| independente do valor da frequência ω. Desta forma,
os diagramas de Bode de magnitude destes dois sistemas serão
idênticos. No entanto, o mesmo não ocorrerá com o diagrama de Bode
de fase destes sistemas. Tal fato explica-se mediante a análise das
equações de fase de cada um destes sistemas, ou seja:
Fase G1 ( jω ) = arctan ω − arctan
ω
(8.13)
10
Fase G2 ( jω ) = 180° − arctan ω − arctan
ω
10
(8.14)
Na equação (8.13), para valores de frequência muito
pequenos, a fase de G1 ( jω ) é aproximadamente zero, ocorrendo o
mesmo para valores muito elevados de frequência. Para a função de
transferência (8.12), a fase G2 ( jω ) , para valores de frequência
pequenos, é praticamente 180º. O diagrama de Bode de magnitude e
fase de cada um destes sistemas é apresentado nas Fig. 3.13 e Fig. 3.14.
Apostila de Controle de Conversores Estáticos
PPGEEL
58
Revisão dos Conceitos Básicos de Controle
Bode Diagram
0
System: g1
Frequency (rad/sec): 94.4
Magnitude (dB): -0.0484
-2
-4
-6
Magnitude (dB)
-8
-10
-12
-14
-16
System: g1
Frequency (rad/sec): 0.0231
Magnitude (dB): -20
-18
-20
60
Phase (deg)
System: g1
Frequency (rad/sec): 3.16
Phase (deg): 54.9
30
System: g1
Frequency (rad/sec): 0.0111
Phase (deg): 0.794
System: g1
Frequency (rad/sec): 758
Phase (deg): 0.863
0
10
-2
10
-1
0
1
10
10
10
2
3
10
Frequency (rad/sec)
Fig. 3.13 - Diagrama de Bode do sistema descrito pela FT da equação
(3.10)
Bode Diagram
0
System: g2
Frequency (rad/sec): 295
Magnitude (dB): -0.00505
-2
-4
Magnitude (dB)
-6
-8
-10
-12
-14
-16
System: g2
Frequency (rad/sec): 0.0141
Magnitude (dB): -20
-18
-20
180
System: g2
Frequency (rad/sec): 0.0131
Phase (deg): 179
Phase (deg)
135
90
45
System: g2
Frequency (rad/sec): 846
Phase (deg): 1
0
10
-2
-1
10
0
10
10
1
2
10
10
3
Frequency (rad/sec)
Fig. 3.14 - Diagrama de Bode do sistema descrio pela FT da equação
(3.11)
3.2.2
3.2.2.1
Margem de fase
Introdução
No projeto de sistemas de controle em malha fechada é muitas
vezes necessário analisar mais profundamente a questão da estabilidade.
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
59
Em particular, é normalmente desejável obter medidas de quão longe da
instabilidade está o sistema nominal em malha fechada, ou seja, é
necessário quantificar a estabilidade relativa do sistema em malha
fechada.
Esta quantificação pode obter-se definindo medidas da distância
da resposta em frequência do sistema nominal ao ponto de estabilidade
crítica (-1,0).
Observação: Essas medidas servem para quantificar a tolerância
na aquisição de componentes, colocar limites no desgaste admissível de
peças, etc. Assumem um sistema nominal estável e quantificam algumas
distâncias à estabilidade crítica.
3.2.2.2
Margens de Ganho ( GM ):
É a faixa de ganho que se pode incrementar ou decrementar a
curva de resposta em frequência de módulo da função de transferência
de malha aberta (de laço) de um sistema até que se alcance o ponto de
estabilidade crítica. Neste ponto o sistema ainda será estável em malha
fechada. A margem de ganho é medida na frequência em que a fase
cruza por -180º:
GM G ( jωM ) H ( jωM ) = 1
(8.15)
A (8.15) também pode ser reescrita para que a margem de ganho
seja expressa em decibéis, como pode ser visto na (8.16):
GMdB = 20 log
1
= −20 log G ( jωM ) H ( jωM )
G ( jωM ) H ( jωM )
(8.16)
Onde: ωM é a frequência em que a fase de G ( jωM ) H ( jωM ) é
igual a 180º.
Definições:
Margem de Ganho Positiva ( GM +): Ganho em decibéis que se
deve somar para levar o sistema à condição de estabilidade crítica.
Margem de Ganho Negativa ( GM -): Ganho em decibéis que se
deve subtrair para levar o sistema à condição de estabilidade crítica.
Frequência de cruzamento de ganho (Wcg): Corresponde ao
ponto em que o ganho cruza a linha de zero decibel no diagrama de
módulo.
Frequência de cruzamento de fase (Wcp): Corresponde ao ponto
em que a fase cruza a linha de -180 graus no diagrama de fase.
Apostila de Controle de Conversores Estáticos
PPGEEL
60
Revisão dos Conceitos Básicos de Controle
Margem de Fase (MF):
É o valor angular a ser acrescido ou decrescido à curva de fase da
resposta em frequência de um sistema operando em malha aberta na
frequência em que a curva de módulo da resposta em frequência deste
mesmo sistema apresenta valor unitário (ou 0.0 dB). Com isso, acaba
indicando quanto a fase do sistema pode ser atrasada (na frequência de
cruzamento de ganho) de forma que o sistema ainda seja estável em
malha fechada.
φM = 180° + arg {G ( jω0 dB ) H ( jω0 dB )}
(8.17)
Onde: ω0dB é a frequência em que o módulo de G ( jωM ) H ( jωM ) é
igual a 1 (0 dB).
Informações associadas às Margens de Ganho e de Fase podem
ser obtidas diretamente dos diagramas de Bode. Para exemplificar essa
análise, será utilizada uma ferramenta computacional, o MATLAB. O
MATLAB (abreviatura de Matrix Laboratory) é um programa para
desenvolvimento e implementação de algoritmos numéricos ou
simbólicos que oferece ao usuário um ambiente interativo de
programação para estudo e pesquisa nas diversas áreas das ciências
exatas. Considera-se, doravante, que o leitor possui conhecimento
básico desta ferramenta.
Exemplo 1:
Para o sistema disposto na Fig. 3.15, serão obtidas as margens de
fase e ganho do sistema para os casos em que K = 10 e K = 100.
Fig. 3.15 - Sistema proposto para análise das margens de ganho e fase
Análise do sistema para K=10:
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
61
Conforme comentado anteriormente, serão utilizados comandos
específicos do programa MATLAB para definir o diagrama de bode do
sistema, e assim, analisar as margens de ganho e fase.
%Define a Função Transferência a ser analisada:
Gs_10=tf([10],[conv([1 0],conv([1 1],[1 5]))])
%Armazena os dados relevantes da FT: margem de
ganho, fase, frequências de % cruzamento.
[Gma,Pma,Wcga,Wcpa] = MARGIN(Gs_10)
%Plota o Diagrama de bode para visualização dos
Dados.
MARGIN(Gs_10)
Bode Diagram
Gm = 9.5424 dB (at 2.2361 rad/sec), Pm = 25.39 deg (at 1.2271 rad/sec)
50
System: Gs_10
Frequency (rad/sec): 2.26
Magnitude (dB): -9.77
Magnitude (dB)
0
-50
-100
-150
-90
Phase (deg)
-135
-180
System: Gs_10
Frequency (rad/sec): 1.22
Phase (deg): -154
-225
-270
-1
10
10
0
10
1
10
2
Frequency (rad/sec)
Fig. 3.16 - Diagrama de Bode do sistema para K=10
Análise do sistema para K=100
Do mesmo modo que utilizado no item a, neste caso, o diagrama
de bode, e a análise do sistema, também foram implementados com a
ajuda do MATLAB:
Apostila de Controle de Conversores Estáticos
PPGEEL
62
Revisão dos Conceitos Básicos de Controle
%Define a Função Transferência a ser analisada:
Gs_100=tf([100],[conv([1 0],conv([1 1],[1 5]))])
%Armazena os dados relevantes da FT: margem de
ganho, fase, frequências de
%cruzamento.
[Gmb,Pmb,Wcgb,Wcpb] = MARGIN(Gs_100)
%Plota o Diagrama de bode para visualização dos
Dados.
MARGIN(Gs_100)
Bode Diagram
Gm = -10.458 dB (at 2.2361 rad/sec), Pm = -23.65 deg (at 3.9073 rad/sec)
50
Magnitude (dB)
System: Gs_100
Frequency (rad/sec): 2.27
Magnitude (dB): 10.2
0
-50
-100
-90
Phase (deg)
-135
System: Gs_100
Frequency (rad/sec): 3.86
Phase (deg): -203
-180
-225
-270
-1
10
0
1
10
2
10
10
Frequency (rad/sec)
Fig. 3.17 - Diagrama de Bode do sistema para K=100
Comparando os resultados da obtidos, tem-se:
Ganho absoluto (dB)
Fase (graus)
Frequência Cruzamento
(Ganho) (rad/sec)
Frequência Cruzamento –
Fase (rad/sec)
K=100(Instável)
Gma = 0.3000(10 dB)
Pma = -23.6504
Wcga = 2.2361
K=10(Estável)
Gmb = 3 (9 dB)
Wcpa = 3.9073
Wcpb =1.2271
Apostila de Controle de Conversores Estáticos
Pmb =25.3898
Wcgb =2.2361
PGEEL
Revisão dos Conceitos Básicos de Controle
63
Lembrando:
Critério de estabilidade do Bode, Gm >1 ⇔ estabilidade
Critério de estabilidade Bode, MF >0 ⇔ estabilidade
Exemplo 2:
No exemplo anterior, foi disponibilizado o diagrama de blocos
do sistema, com suas respectivas funções de transferência. Mas, em
casos onde não há função de transferência, apenas o comportamento do
diagrama de bode, em relação à estabilidade do sistema, é importante
definir quanto se pode atrasar a fase para que chegue a -180º.
Bode Diagram
40
Magnitude (dB)
30
20
10
0
-10
-20
Phase (deg)
-90
-135
-180
10
-1
10
0
10
1
Frequency (rad/sec)
Fig. 3.18 - Diagrama de Bode de um sistema não especificado
Percebe-se que a frequência para a qual o módulo é 0 dB é
wg ≅ 4.2544 rad s . Neste ponto a fase cruza em -155º. O valor para a
margem de fase, neste caso, é φmf = 25° . Sendo a margem de fase
positiva, então o sistema será estável em malha fechada.
Dessa maneira, é possível afirmar que se este sistema for
submetido a uma entrada em degrau unitário, a curva de resposta em
malha fechada tenderia a estabilização. Na Fig. 3.19 está o
comportamento esperado deste sistema para esta condição:
Apostila de Controle de Conversores Estáticos
PPGEEL
64
Revisão dos Conceitos Básicos de Controle
Step Response
1.5
Amplitude
1
0.5
0
0
1
2
3
4
5
6
7
8
9
10
Time (sec)
Fig. 3.19 - Resposta à entrada degrau do sistema analisado no exemplo
2
3.2.2.3
Resumo Utilização dos Diagramas de Bode para análise da
margem de ganho e de fase:
Vantagens:
1- Na ausência de um computador, o diagrama de Bode pode ser
obtido, de forma aproximada, através de suas propriedades assintóticas.
2- Ganho de cruzamento, fase de cruzamento, margem de ganho e
margem de fase são mais facilmente determinados no gráfico de Bode
do que no gráfico de Nyquist1.
3- Para propósitos de projeto, os efeitos de adição de
controladores e seus parâmetros são mais facilmente visualizados no
gráfico de Bode do que no gráfico de Nyquist1.
[15] – Desenvolvido por Harry Nyquist (1932) nos laboratórios
Bell, os diagramas de Nyquist são diagramas polares, enquanto os
diagramas de Bode são diagramas retangulares. Este diagrama também é
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
65
comumente usado para a representação de sistema de controle com
retroações lineares e invariantes no tempo, no domínio da frequência.
Desvantagens:
1- A estabilidade absoluta e relativa podem ser determinadas
através do diagrama de Bode somente para sistemas de fase mínima, na
qual, sua função de transferência apresenta todos os seus pólos e zeros
localizados no semiplano esquerdo do plano s.
3.2.3
3.2.3.1
Lugar das raízes
Introdução
O método do Lugar Geométrico das Raízes foi desenvolvido por W.
R. Evans [15] e apresentado em um artigo publicado em 1948. Este
método tem por objetivo representar graficamente o deslocamento dos
pólos de malha-fechada de um sistema linear quando sujeito a variação
de um ou mais parâmetros. O método do LGR é muito eficiente para a
análise e projeto de sistemas de controle lineares, permitindo concluir
aspectos relacionados a estabilidade e a resposta transitória destes
sistemas.
3.2.3.2
Utilização e Aplicação
A principal vantagem deste método é que as raízes da equação
característica podem ser obtidas diretamente. Daí resulta a solução
completa da resposta transitória e da resposta em regime permanente da
variável controlada.
Seja o diagrama mostrado na Fig. 3.20 um representante genérico
de um sistema de controle.
Apostila de Controle de Conversores Estáticos
PPGEEL
66
Revisão dos Conceitos Básicos de Controle
Fig. 3.20 - Diagrama de Blocos Genérico de um sistema de controle
realimentado
Sua função transferência de Malha Fechada é definida como:
C (s)
Gc ( s )Gi ( s )
=
R( s ) 1 + Gc( s )Gi ( s ) H ( s )
(8.18)
Onde: 1 + Gc( s)Gi ( s) H ( s) = 0 é sua equação característica.
A característica básica da resposta transitória de um sistema em
malha fechada depende essencialmente dos pólos de malha fechada.
Estes são definidos como sendo as raízes da equação característica do
sistema (mostrada acima).
O método do lugar das raízes é um método pelo qual as raízes da
equação característica são colocadas em um gráfico para todos os
valores de um parâmetro do sistema. As raízes correspondentes a um
valor particular deste parâmetro podem então ser localizadas no gráfico
resultante. Note que o parâmetro usualmente é o ganho, porém qualquer
outra variável da função de transferência em malha aberta pode ser
utilizada. Salvo menção em contrário, é considerado que o ganho da
função de transferência em malha aberta é o parâmetro a ser variado
através de todos os seus valores, isto é, de zero a infinito.
A estabilidade do sistema poderá ser analisada verificando a partir
de qual valor de ganho K teremos raízes no semiplano direito do gráfico.
Quando forem observadas raízes no semiplano direito do gráfico,
teremos a instabilidade do sistema.
3.2.3.3
Regras de Construção de um LGR
O procedimento de Evans para construir o LGR consiste de uma
coleção de regras para determinar se o ponto de teste, St , no plano
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
67
complexo é um pólo de malha-fechada do sistema para algum valor de
K.
Regra 1: Os pólos de malha aberta são todos pontos do LGR
correspondentes ao ganho K = 0.
Regra 2: O número de ramos do LGR é exatamente igual à
quantidade de raízes do denominador da função de transferência em
malha-fechada.
Regra 3: Para K ≥ 0, qualquer ponto do eixo real que ficar a
esquerda de um número impar de singularidades (pólos ou zeros)
localizadas também no eixo real é um ponto do LGR (Esta regra pode
ser comprovada aplicando a condição angular (8.19), para testar pontos
no eixo real).
G ( s ) H ( s ) = ±(2h + 1)180°
(8.19)
Onde h=0,1,2,...
Regra 4: O LGR é simétrico em relação ao eixo real.
Regra 5: Se G(s) tem n pólos e m zeros finitos (m ≤ n) então
exatamente m ramos terminam, quando k → ∞ , em zeros finitos. Os
ramos remanescentes (n-m) tendem ao infinito para k → ∞ .
A validade desta regra pode ser mostrada fazendo-se o limite para
k → ∞ , da (8.20), ou seja:
lim k →∞ G ( s ) H ( s ) = lim k →∞
1
=0
k
(8.20)
Portanto para k → ∞ , é verdadeiro afirmar que G ( s) H ( s) → 0 , e
para que isto ocorra, o valor de s deve ser qualquer zero finito de G ( s) .
Regra 6: Se G ( s) tem n pólos e m zeros finitos (m ≤ n) então os
(n – m) ramos tendem assintoticamente, quando k → ∞ , para uma reta
que intercepta o eixo real no ponto σ o e que forma um ângulo γ com o
mesmo eixo real, onde:
γ =±
(1 + 2h)180°
n−m
(8.21)
Onde h=0,1,2,...
Apostila de Controle de Conversores Estáticos
PPGEEL
68
σo
Revisão dos Conceitos Básicos de Controle
∑
=
n
i =1
Re( pi ) − ∑ l =1 Re( zl )
m
n−m
(8.22)
Regra 7: O cálculo dos pontos de entrada e de saída do Lugar
Geométrico das Raízes no eixo real do plano s é realizado com base na
equação (8.23), descrita abaixo:
dG ( s ) H ( s )
=0
ds
(8.23)
Regra 8: Nos casos em que o LGR do sistema, em análise,
apresenta raízes sobre o eixo imaginário, o valor do ganho K necessário
para que ocorra tal situação poderá ser determinado empregando-se o
critério de estabilidade de Routh-Hurwitz2.
[16] O critério de Routh-Hurwitz é um método algébrico que
informa acerca da estabilidade absoluta de um sistema linear invariante
no tempo, testando se há alguma raiz da equação característica no semiplano direito do plano s. O método também indica quantas raízes estão
sobre o eixo imaginário e quantas estão no semi-plano direito.
A fim de melhor abstrair a teoria repassada até o momento, será
utilizado um exemplo, para detalhar os passos a serem desenvolvidos
para definição do LGR. Considere o sistema de controle com
realimentação não unitária, mostrado na Fig. 3.21.
Fig. 3.21 - Sistema de controle com realimentação não unitária
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
69
Root Locus Editor for Open Loop 1 (OL1)
30
0.76
0.64
0.5
0.34
0.16
0.86
20
0.94
10
Imag Axis
0.985
40
0
35
30
25
20
15
10
5
0.985
-10
0.94
-20
0.86
0.76
-30
-40
0.64
-30
0.5
-20
0.34
0.16
-10
Real Axis
0
10
20
Fig. 3.22 - LGR do Sistema apresentado na Fig. 3.21
1º passo: Função de transferência de malha aberta:
G1 ( s ) H1 ( s ) =
100 K1
(8.24)
 s ⋅ ( s + 15s + 50) 
2
Os pólos da função de transferência de malha aberta são:
p1 = 0, p2 = −5 e p3 = −10
2º passo: Função de transferência de malha fechada:
T1 ( s ) =
G1 ( s )
100 K1 ( s + 5)
=
3
1 + G1 ( s ) H1 ( s ) ( s + 15s 2 + 50s + 100 K1 ) 


(8.25)
Equação característica:
1 + G1 ( s ) ⋅ H1 ( s ) = s 3 + 15s 2 + 50s + 100 K1
O erro em regime, para uma entrada do tipo degrau unitário, é:
y1 (∞ ) = lim s → 0 sY ( s ) = lim s → 0 sU ( s )T1 ( s ) =
500 K1
=5
100 K1
e(∞) = u (∞ ) − y (∞) = 1 − 5 = −4
(8.26)
(8.27)
Na Fig. 3.23, pode-se verificar a existência de um erro constante
em regime, além disso, se o sistema for estável, este erro não depende
do ajuste do ganho K1.
Apostila de Controle de Conversores Estáticos
PPGEEL
70
Revisão dos Conceitos Básicos de Controle
Step Response
6
5
Amplitude
4
3
2
1
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time (sec)
Fig. 3.23 - Resposta temporal do sistema da Fig. 3.21 para K1=1
3º passo: Grau relativo do sistema: n − m = 3 − 0 = 0
4º passo: Traçado das assíntotas:
Centroide:
∑
σo =
n
i =1
Re( pi ) − ∑ l =1 Re( zl )
m
n−m
=
0 − 5 − 10
= −5
3
(8.28)
Ângulos:
γ =±
(1 + 2h)180°
, onde h=0, 1, 2,..
n−m
(8.29)
γo =
180
= 60°
3
(8.30)
γ1 =
3 ⋅180
= 180°
3
(8.31)
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
γ2 =
5 ⋅180
= 300° = −60°
3
71
(8.32)
5º passo: Ponto de partida do LGR:
2
d (G1 ( s ) H1 ( s )) d 
100
 (3s + 30 s + 50) ⋅100 − 0
=  3
=

ds
ds  s + 15s 2 + 50 s 
( s 3 + 15s 2 + 50s ) 2
(8.33)
3s 2 + 30 s + 50 = 0
(8.34)
{r1 = − 2.11
{r2 = −7.88
(8.35)
Como o ponto r2 = −7.88 não pertence ao LGR, o ponto de
partida é r1 = −2.11 . Para obter o valor do ganho K1 para que a resposta
do sistema não apresente oscilação, calcula-se a contribuição dos pólos
(e zeros se houver) no ponto de partida –2.11. A Fig. 3.24, mostra a
resposta temporal quando os pólos em malha fechada estão localizados
em –2.11.
100 K1 = 2.11 ⋅ (5 − 2.11) ⋅ (10 − 2.11) → K1 = 0.4811
Apostila de Controle de Conversores Estáticos
(8.36)
PPGEEL
72
Revisão dos Conceitos Básicos de Controle
Step Response
6
5
Amplitude
4
3
2
1
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time (sec)
Fig. 3.24 - Resposta temporal do sistema da Fiug. 3.21 para K1=0.4811
6º passo: Faixa de ganho em que o sistema é estável.
Q1 ( s ) = s 3 + 15s 2 + 50s + 100 K1
s3
s
2
s1
s0
1
50
15
100 K1
750 − 100 K1
15
100 K1
0
Logo, para K1 ≥ 0 e K1 ≤ 7.5 , o sistema é estável.
7º passo: Determinação dos pólos de malha fechada.
Substituindo o valor de K1 = 7.5 na equação característica obtêmse os valores das raízes quando o sistema é marginalmente estável:
Apostila de Controle de Conversores Estáticos
PGEEL
Revisão dos Conceitos Básicos de Controle
73
 r1 = − j 7.07

Q1 ( s ) = s + 15s + 50 s + 750  r2 = + j 7.07
 r = −15
 3
3
2
Substituindo o valor de K1 = 1 na equação característica obtêm-se
os valores dos pólos em malha fechada:
 r1 = −1.811 − j 2.347

( I o ) Q1 ( s ) = s + 15s + 50s + 100 r2 = −1.811 + j 2.347
 r = −11.378
 3
3
2
Com base nestes dados, é possível chegar ao esboço do LGR
deste sistema, disposto na Figura 22. Contudo, há diversas
particularidades vinculadas ao esboço do LGR, e mesmo seguindo as
regras sugeridas anteriormente, é necessário muita prática para esboçar
rapidamente o LGR de um dado sistema. Dessa forma, também é
interessante consultar outras referências bibliográficas para analisar
outros casos dos diagramas de lugares das raízes.
3.2.3.4
Observações:
1)A introdução de um zero à esquerda dos pólos tem por efeito
deslocar o lugar das raízes para a esquerda, tendendo a tornar o sistema
mais estável e com menor tempo de acomodação.
2)A introdução de um pólo à esquerda tem por efeito deslocar o
LGR para a direita, tendendo a tornar o sistema menos estável e com
maior tempo de acomodação.
3.2.3.5
Procedimento Resumido para aplicação do Método do
Lugar das Raízes - LGR:
1 – Determinar a função transferência de malha aberta G(s)H(s)
do sistema.
2 – Fatorar o numerador e o denominador de G(s)H(s) em termos
da forma “s+a”, onde “a” pode ser real ou complexo.
3 – Assinalar os pólos e zeros de G(s)H(s) no plano s=σ+jω.
4 – Os pólos e zeros de G(s)H(s) determinam as raízes da
equação característica [1+G(s)H(s)=0] da função de transferência de
malha fechada.
5 – Graduar o lugar das raízes em função dos valores do ganho K.
Apostila de Controle de Conversores Estáticos
PPGEEL
74
Revisão dos Conceitos Básicos de Controle
a) Se o ganho for preestabelecido, sabe-se imediatamente a
localização das raízes.
b) Se a localização das raízes de [1 + G(s)H(s) = 0] for
estabelecida, pode-se obter o ganho K.
6 – Determinadas as raízes de [1 + G(s)H(s) = 0], pode-se
calcular a resposta do sistema tomando-se a transformada inversa de
Laplace.
7 – Se a resposta não atender às especificações de desempenho
desejado, determinar a forma que o LGR deveria apresentar para atendêlas.
8 – Sintetizar a estrutura a ser acrescentada ao sistema a fim de
produzir a modificação pretendida do LGR original: compensação do
LGR.
Apostila de Controle de Conversores Estáticos
PGEEL
Modelagem de conversores em condução descontínua
4
75
Modelagem do conversor BUCK em condução contínua
[20] [21] [22]
4.1 Introdução
Neste capítulo são apresentados os modelos dos conversores
BUCK, BOOST e BUCK-BOOST operando no modo de condução
contínua. Para os três conversores serão apresentados os modelos de
tensão e modelo de corrente em função da razão cíclica e apenas para o
BUCK e BOOST serão apresentados o modelo de tensão em função da
corrente.
Antes da apresentação dos modelos dos Conversores em
condução contínua, serão apresentadas as etapas de operação dos
conversores para melhor entendimento do equacionamento.
Ainda, com o objetivo de completar e validar o estudo, para cada
modelo de conversor, será apresentada uma simulação feita no software
PSIM (Power Simulator) e seus resultados bem como comentários sobre
os resultados obtidos.
4.2
Modelagem do Conversor BUCK em Modo de
Condução Contínua
Os conversores cc-cc são utilizados para controlar o fluxo de
energia entre dois sistemas de corrente contínua. O conversor BUCK é
um conversor utilizado quando se deseja obter uma tensão de saída
menor do que a tensão de entrada. Ou seja, converte uma tensão cc de
entrada em uma tensão de saída também cc de valor menor.
Esses conversores são utilizados principalmente em fontes de
alimentação chaveadas e para controle de velocidade de motores de
corrente contínua. Alguns conversores que empregam o modelo do
conversor Buck são: Forward, Conversor meia ponte com comutação
suave, conversor ponte completa com comutação suave, conversor 3
níveis com comutação, inversores de tensão com filtro LC. Os circuitos
desses conversores podem ser vistos nas figuras a seguir.
Apostila de Controle de Conversores Estáticos
PPGEEL
76
Modelagem de conversores em condução descontínua
Fig. 4.1 – Circuito do conversor Forward empregando o modelo do
conversor BUCK.
Fig. 4.2 – Circuito do conversor meia ponte com comutação suave
empregando o modelo do conversor BUCK.
Fig. 4.3 – Circuito do conversor ponte completa com comutação suave
empregando o modelo do conversor BUCK.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
77
Fig. 4.4 – Circuito do conversor 3 níveis com comutação suave
empregando o modelo do conversor BUCK.
Fig. 4.5 – Circuito do conversor 3 níveis com comutação suave
empregando o modelo do conversor BUCK.
O circuito básico do conversor BUCK pode ser representado pela
Fig. 4.6. A fonte de tensão de entrada contínua é representada por Vg, o
indutor e o diodo de roda livre são, respectivamente, L e D. Na saída o
filtro RC é representado pelo capacitor C e o resistor R. Tal filtro RC em
muitas literaturas é representado por V0 (tensão de saída) visto que a
tensão no filtro é constante, quando a razão cíclica for, e facilita a
análise da tensão de saída em função da tensão de entrada (modelo cc).
Apostila de Controle de Conversores Estáticos
PPGEEL
78
Modelagem de conversores em condução descontínua
Fig. 4.6 – Circuito do conversor BUCK em condução contínua.
O circuito do conversor Buck tem duas etapas de operação. Na
primeira etapa, representada pela Fig. 4.7, a chave S está fechada e o
diodo D está inversamente polarizado e pode ser desconsiderado na
analise. O capacitor C está sendo carregado.
Fig. 4.7 – Conversor BUCK na primeira etapa de operação: chave S
fechada.
Na segunda etapa, representada pela Fig. 4.8, a chave S está
aberta, excluindo assim a fonte Vg do circuito. Já o diodo de roda-livre
D entra em funcionamento fazendo com que a corrente no indutor,
exclusiva da energia acumulada no mesmo, passe a fluir pela carga e os
demais componentes. A corrente no indutor cresce do valor mínimo até
o valor máximo com característica linear e derivada dada por
Apostila de Controle de Conversores Estáticos
Vg − V
L
.
PPGEEL
Modelagem de conversores em condução descontínua
79
Fig. 4.8 - Conversor BUCK na segunda etapa de operação: chave S
aberta.
Para a primeira etapa de operação, são válidas as seguintes
equações:
vL (t ) = vg (t ) − v(t )
iC (t ) = iL (t ) − iR (t ) = iL (t ) −
(9.1)
v(t )
R
(9.2)
ig (t ) = iL (t )
(9.3)
Para a segunda etapa, são válidas as seguintes equações:
vL (t ) = −v(t )
iC (t ) = iL (t ) − iR (t ) = iL (t ) −
(9.4)
v(t )
R(t )
ig (t ) = 0
(9.5)
(9.6)
As etapas de funcionamento do circuito do Buck, que estão
representadas pelas equações acima, também podem ser representadas
pelas formas de onda mais básicas do conversor cc-cc Buck na Fig 4.9.
Apostila de Controle de Conversores Estáticos
PPGEEL
80
Modelagem de conversores em condução descontínua
Fig. 4.9 – a) Tensão sobre o diodo D - b) Corrente sobre o indutor L c) Corrente sobre a fonte de tensão de entrada Vg - d) Corrente sobre o
diodo D. Intervalos de tempo: “ton” – primeira etapa onde a chave S
está fechada e o diodo esta inversamente polarizado. “toff” – segunda
etapa onde a chave S está aberta e o diodo esta em roda livre. “T”
período de comutação.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
4.3
81
Modelo de Tensão do Conversor BUCK v(s) / d(s)
A tensão média no diodo para o modo de condução contínua é:
Vg D , onde Vg é a tensão de entrada e D a razão cíclica. Sendo assim,
pode-se considerar o modelo da Fig. 4.10 para a análise e obtenção da
função de transferência (FT) do conversor Buck.
Fig. 4.10 - Modelo simplificado do conversor BUCK para obtenção da
FT.
Nesse estado topológico as seguintes equações são verdadeiras:
 Ldi (t ) 
−Vg .D +  l  + v(t ) = 0
 dt 
il (t ) = ic (t ) +
ic (t ) =
v (t )
R
Cdv(t )
dt
(9.7)
(9.8)
(9.9)
Onde il e ic são as correntes no indutor e no capacitor,
respectivamente. A tensão de saída é a própria tensão no capacitor,
representada por vc.
Substituindo as equações (4.7) e (4.8) na equação (4.9) chega-se
na equação (4.10) abaixo:
L.C.
d 2 v(t ) L dv(t )
+ .
+ v(t ) = Vg .D
dt 2
R dt
Apostila de Controle de Conversores Estáticos
(9.10)
PPGEEL
82
Modelagem de conversores em condução descontínua
Para continuação do equacionamento será necessário introduzir o
conceito de valor médio instantâneo: definindo como o valor médio de
uma grandeza em um período de comutação Ts. Assim, por exemplo,
para a corrente no indutor tem-se:
il (t )
Ts
=
t +Ts
1
= ∫ τ dτ
Ts t
(9.11)
Em regime permanente a tensão média do indutor e a corrente
média do capacitor são nulas. Ainda, as correntes e tensões médias são
funções não lineares da razão cíclica. A representação média do circuito
para um conversor chaveado é muito útil para análise e simulação do
conversor.
A hipótese básica considerada é que as constantes de tempo do
conversor são muito maiores que o período de comutação Ts. Pode-se
realizar a média das formas de onda em um intervalo de tempo
suficientemente curto se comparado com as constantes de tempo do
conversor, sem alterar significativamente a resposta do sistema. Desta
forma, o modelo médio resultante prediz o comportamento em baixa
freqüência do conversor, enquanto despreza as harmônicas em alta
freqüência produzidas pelas comutações.
Perturbações: muitas plantas não são lineares, o que dificulta o
emprego das técnicas de controle conhecidas. Com a aplicação da
técnica de modelagem em pequenos sinais são obtidos modelos lineares,
através da linearização em torno de um ponto de operação. Provoca-se
uma pequena variação, ou perturbação na variável de entrada e esta
variação provoca uma perturbação na variável de saída, considerada
nesse método, linearizada.
A analise despreza a variação de alta freqüência, resultado da
comutação do conversor. A interferência do chaveamento é subtraída da
análise pelo calculo do valor médio das variáveis em um período de
chaveamento. Considera-se o efeito de uma pequena variação no sinal
de entrada.
Em síntese, aplicando uma perturbação no sistema(escrevendo o
sinal como seu valor médio mais uma pequena variação), representadas
pelas equações (4.12) até (4.14), chega-se na equação (4.15):
^
d (t ) = D + d (t )
(9.12)
^
Vg (t ) = Vg + vg (t )
Apostila de Controle de Conversores Estáticos
(9.13)
PPGEEL
Modelagem de conversores em condução descontínua
83
^
v(t ) = V + v(t )
(9.14)
Onde:
^
D >> d (t )
^
I >> il (t )
^
Vg >> vg (t )
^
^




^
^
V + v(t )  L V + v(t ) 

L.C.d
+
.
d
+
V
+
v
(
t
)
=
V
.
D
+
v
g (t )
g
 dt 2  R  dt 




2
(9.15)
Separando apenas os termos CC da equação (4.15), chega-se na
equação que define o modelo do conversor BUCK (modelo CC),
conforme equação (4.16):
L.C.d 2
V
L V
+ .d + V = Vg .D
2
dt
R dt
(9.16)
Como a derivada de uma constante é igual à zero, a equação
(4.16) pode ser reescrita como:
V = Vg .D
(9.17)
V
=D
Vg
(9.18)
Agora separando apenas os termos CA da equação (4.15) e em
seguida aplicando Laplace, encontra-se a planta de tensão V(s) em função
da razão cíclica d(s) do conversor BUCK:
Equação (4.15) escrita apenas em termos CA:
^
^
^
d 2 v(t ) L d v(t )
L.C.
+ .
+ V = v g (t )
2
dt
R dt
L
L.C.s 2 v( s ) + .s.v( s ) + v( s ) = Vg .d ( s )
R
Apostila de Controle de Conversores Estáticos
(9.19)
PPGEEL
84
Modelagem de conversores em condução descontínua
L.s 

v( s ).  L.C.s 2 +
+ 1 = Vg .d ( s )
R


Vg
v( s)
=
d ( s ) L.C.s 2 + L.s + 1
R
(9.20)
(9.21)
A equação (9.21) define a planta de tensão do conversor BUCK
em função da razão cíclica. Para baixas freqüências, vale a análise cc
representado pela equação (9.18).
Para comprovar o equacionamento, tal planta será simulada no
PSIM, juntamente com o circuito BUCK apropriadamente projetado
para que sejam comparados os resultados. Para validar essas simulações
e também a planta de tensão obtida acima é interessante que sejam
aplicados degraus na razão cíclica, ou então na carga conversor. Como o
conversor BUCK é um conversor linear, é esperado que os resultados
obtidos nas simulações da planta e do circuito para a resposta ao degrau
sejam bem próximos.
4.3.1
Simulação da Planta de tensão em função da razão
cíclica V(s) / d(s)
A tabela 4.1 apresenta os parâmetros do conversor BUCK usado
na simulação no PSIM. Como o foco desse estudo não é o projeto do
conversor e sim a modelagem do conversor BUCK, os cálculos do
projeto do conversor estão omitidos.
Tabela 4.1 - Parâmetros do conversor Buck
Especificações dos Componentes
Tensão de Saída (V0)
48V
Tensão de Entrada (Vi)
400V
Potencia de Saída ( Pout )
1kW
Freqüência de Comutação ( f s )
20kHz
Razão Cíclica para MCC ( D )
0,12
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
85
Resistor
2,3Ω
Capacitor
100µF
Indutor
500µH
Para verificar o comportamento da planta de tensão foi simulado
o conversor com variações na razão cíclica.
Fig. 4.11 – Circuito do conversor Buck e planta V0(s)/d(s) simulado no
PSIM.
O Fig. 4.11 representa o circuito do conversor Buck operando em
modo de condução contínua simulado no PSIM. A parte mais abaixo da
figura esta representada o circuito propriamente dito, onde estão
representados a fonte de entrada Vin, o indutor L, o capacitor C e o
resistor R, cujos valores encontram-se na Tabela 4.1.
Na parte superior da figura, estão representados a planta de
tensão em função da razão cíclica (H(s)) e também o sinal da chave:
referencia e portadora. Em série com o sinal de referencia esta um
degrau que será aplicado no sistema, para verificar a resposta do sistema
ao degrau. O sinal da portadora é representado por um sinal dente de
serra.
Apostila de Controle de Conversores Estáticos
PPGEEL
86
Modelagem de conversores em condução descontínua
Fig. 4.12 - V0 para simulação PSIM sem degrau.
Fig. 4.13 - V0 simulação PSIM com d(s) = 10%: tensão de
saída do circuito (vermelho) e tensão de saída da planta simulada
(azul).
Fig. 4.14 – V0 simulação PSIM com d(s) = 20%: tensão de saída do
circuito (vermelho) e tensão de saída da planta simulada (azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
87
Fig. 4.15 - V0 simulação PSIM com d(s) = 50%: tensão de saída do
circuito (vermelho) e tensão de saída da planta simulada (azul).
Fig. 4.16 – Dente de Serra e referencia para uma variação na razão
cíclica de 50%.
Nas figuras anteriores foram aplicados degraus de 10%, 20% e
50%, em relação a razão cíclica, na referencia do sinal da chave do
circuito do Buck. Com isso, a tensão se estabilizou em 52,8V, 57,6V e
72V respectivamente. Uma vez que o circuito e a planta do conversor
Buck são naturalmente estáveis, mesmo com uma variação de 50% da
razão cíclica, o sistema não se torna instável.
4.4
Modelo de Corrente do Conversor BUCK I0(s) / d(s)
Na maioria dos conversores é adotada a topologia de controle da
corrente no indutor, uma vez que a medição de corrente pode ser feita de
maneira direta. Desse modo, é necessário que a planta de corrente do
conversor seja definida com o objetivo de conhecer seu comportamento
em malha aberta e posteriormente escolher o controle que mais se
Apostila de Controle de Conversores Estáticos
PPGEEL
88
Modelagem de conversores em condução descontínua
adequar para a planta. Sendo assim, reescrevendo a equação (9.1), temse:
 Ld (t ) 
v(t ) = Vg .D −  il 
 dt 
(9.22)
Substituindo a equação (9.22) em (9.2):
di (t ) 
1 
. Vg .D − L. l 
R 
dt 
(9.23)
di (t ) 
dv(t ) 1 
+ . Vg .D − L. l 
dt
R 
dt 
(9.24)
il (t ) = ic (t ) +
il (t ) = C.
Derivando a equação (9.22) e substituindo na equação (9.24):
il (t ) = C.
dVg (t ).D
dt
− CL.
d 2il (t ) 1 
di (t ) 
+ . Vg .D − L. l 
2
dt
R 
dt 
(9.25)
dV (t ).D Vg .D
d 2il (t ) L dil
CL.
+ . + il (t ) = C. g
+
2
dt
R dt
dt
R
(9.26)
Para que seja possível modelar a planta de corrente em função da
razão cíclica é necessário que seja aplicado uma perturbação na equação
(9.26) acima, depois separado apenas a parte CA do sistema (9.27) e em
seguida aplicado Lapalce (9.28):
^
^
^
^
dVg (t ). d (t ) Vg . d (t )
d 2 il (t ) L d il (t ) ^
CL.
+ .
+ il (t ) = C.
+
2
dt
R dt
dt
R
V
L
CL.s 2 .il ( s ) + .s.il ( s ) + il ( s ) = C.s.Vg .d ( s ) + g d ( s )
R
R
(9.27)
(9.28)
V 

L


il ( s ). CL.s 2 + .s + 1 = d ( s ). C.s.Vg + g 
R
R



(9.29)
V
L


il ( s ). CL.s 2 + .s + 1 = d ( s ). g .[ R.Cs + 1]
R
R


(9.30)
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua


il ( s ) Vg 
R.Cs + 1 
= .

d ( s ) R  CL.s 2 + L .s + 1 


R
89
(9.31)
A equação (9.31) acima define a planta de corrente do conversor
BUCK em função da razão cíclica que será simulado no PSIM para
validação do equacionamento. Em baixas freqüências a corrente do
indutor irá depender da razão entre a tensão de entrada e a resistência de
carga.
4.4.1
Simulação da Planta de corrente em função da razão
cíclica I0(s) / d(s)
Assim como foi feito para planta de tensão em função da razão
cíclica, serão utilizados os parâmetros da Tabela 1 para simular a planta
de corrente em função da razão cíclica. Seguindo na mesma linha, serão
feitas variações na razão cíclica para validar a planta obtida na equação
(4.30).
Fig. 4.17 – Circuito do conversor Buck e planta I0(s)/d(s) simulado no
PSIM.
Apostila de Controle de Conversores Estáticos
PPGEEL
90
Modelagem de conversores em condução descontínua
O circuito acima é praticamente o mesmo representado e
simulado na Fig. 4.11, sendo que a única diferença esta na planta de
corrente em função da razão cíclica, representado por H(s).
Fig. 4.18 - Corrente no indutor do circuito simulado(vermelho) e
corrente no indutor na planta simulada(azul) sem aplicação de degrau.
Fig. 4.19 - Planta de corrente em função de d(s) simulação PSIM com
d(s) = 10%: Corrente no indutor do circuito simulado(vermelho) e
corrente no indutor na planta simulada(azul).
Fig. 4.20 - Planta de corrente em função de d(s) simulação PSIM com
d(s) = 20%: Corrente no indutor do circuito simulado(vermelho) e
corrente no indutor na planta simulada(azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
91
Fig. 4.21 - Planta de corrente em função de d(s) simulação PSIM com
d(s) = 50%: Corrente no indutor do circuito simulado(vermelho) e
corrente no indutor na planta simulada(azul).
Assim como para as simulações da planta de tensão em função da
razão cíclica, a simulação da corrente no indutor em função da razão
cíclica mostrou que, mesmo com variações altas na razão cíclica, ou
degraus, tanto o circuito simulado do Buck, quanto à planta simulada se
mantiveram estáveis. Ainda, a corrente no indutor da planta simulada,
embora apresente um pequeno atraso na resposta ao degrau se
comparado a corrente do indutor do circuito, se apresentou bastante
próxima dos valores esperados, principalmente em regime, o que valida
o equacionamento.
4.5
Modelo de Tensão em função da Corrente do
Conversor BUCK V(s) / I0(s)
Para algumas estratégias de controle, é interessante que seja feito
o controle não só da tensão ou da corrente, mas sim dos dois sinais. Para
isso é acrescentada, por exemplo, uma malha de controle de tensão,
externa ao controle de corrente, onde o sinal de entrada será a própria
corrente. Para que esse sinal possa ser considerado constante para a
malha externa (tensão), é interessante que a malha interna (corrente) seja
muito mais rápida que a malha externa. Nesse capítulo o foco não é o
controle do conversor, mas sim em seu modelo.
Sendo assim, a seguir será apresentado o modelo de V0/IL, que
poderá ser utilizado como planta para malha externa de um controle de
corrente e tensão.
Reescrevendo a equação (9.2) chega-se na equação (9.32):
Apostila de Controle de Conversores Estáticos
PPGEEL
92
Modelagem de conversores em condução descontínua
il (t ) = C.
dv v(t )
+
dt
R
(9.32)
Aplicando uma perturbação em v(t ) e il (t ) :
^
 

^
d
.
V
+
v
(t )  

 
^
V v(t )

I l (t ) + i l (t ) = C. 
+ +
dt
R

 R


(9.33)
Separando os termos CC da equação (9.33):
 d .V  V
I l (t ) = C. 
+
 dt  R
(9.34)
Como a derivada de uma constante é igual a zero, a equação
(9.34) acima pode ser reescrita como:
I l (t ) =
V
R
(9.35)
Agora reorganizando, os termos CA da equação (9.28) e em
seguida aplicando Laplace:
^
^
d . v(t ) v(t )
i l (t ) = C.
+
dt
R
V
I l ( s ) = C.s.V ( s ) + ( s )
R
V ( s)
1
=
I l ( s ) C.s + 1
R
^
(9.36)
(9.37)
(9.38)
A equação (9.38) acima representa a planta de tensão em função
da corrente. Essa equação será simulada junto às funções de tensão e de
corrente em função da razão cíclica para validação dos modelos.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
4.5.1
93
Simulação da Planta de tensão em função da corrente
V(s) / I0(s)
Assim como foi feito para as plantas anteriores, serão utilizados
os parâmetros da Tabela 1 para simular a planta de tensão em função da
corrente. Seguindo na mesma linha, serão feitas variações na razão
cíclica para validar a planta obtida na equação (9.31).
Fig. 4.22 – Circuito do conversor Buck e planta V0(s)/I0(s) simulado no
PSIM.
Novamente, o circuito acima é praticamente o mesmo
representado e simulado na Fig. 4.11, sendo que a única diferença esta
na planta de tensão de saída em função da corrente do indutor que agora
está representado por H(s). Os demais cometários referentes a Fig 4.11
se mantém.
Apostila de Controle de Conversores Estáticos
PPGEEL
94
Modelagem de conversores em condução descontínua
Fig. 4.23 - V0 simulação PSIM se degra: tensão de saída do circuito
(vermelho) e tensão de saída da planta simulada (azul).
Fig. 4.24 - V0 simulação PSIM com degrau de 10%: tensão de saída do
circuito (vermelho) e tensão de saída da planta simulada (azul).
Fig. 4.25 - V0 simulação PSIM com degrau de 20%: tensão de saída do
circuito (vermelho) e tensão de saída da planta simulada (azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
95
Fig. 4.26 - V0 simulação PSIM com degrau de 50%: tensão de saída do
circuito (vermelho) e tensão de saída da planta simulada (azul).
Assim como foi feito para as simulações da planta de tensão em
função da razão cíclica, para a simulação da planta da tensão de saída
em função da corrente no indutor foram aplicados degraus de 10%, 20%
e 50% na referencia do sinal da chave do circuito do Buck. Com isso, a
tensão se estabilizou em 52,8V, 57,6V e 72V respectivamente, como era
de se esperar. Uma vez que o circuito e a planta do conversor Buck são
naturalmente estáveis, mesmo com uma variação de 50% da razão
cíclica, o sistema não se torna instável. Mais uma vez, a planta
encontrada por equacionamento se mostrou válida.
4.6
Conclusões
Através das simulações feitas no PSIM foi comprovada a
validade dos modelos de pequenos sinais do conversor Buck obtidos por
meio de equacionamento. Observando as figuras da planta de tensão em
função da razão cíclica e da tensão em função da corrente no indutor
observa-se nas que a tensão V0 se “estabiliza” em 48V com D=0,12
como era de se esperar e tem resposta rápida ao degrau, além claro de se
manter estável. Isso se deve ao fato do conversor Buck ser um conversor
linear. Com a variação da razão cíclica (10%, 20% e 50%) o sistema
continua se mantendo estável, devido à linearidade do conversor Buck.
Para o caso da planta de corrente em função da razão cíclica a
estabilidade do sistema também é comprovada, pois apenas a função de
transferência mudou e o sistema é o mesmo. Nessa planta a corrente se
estabiliza em 20,87A (VC/R) com D=0,12 e tem resposta estável ao
degrau.
Dessa forma, as simulações obtidas através do PSIM validam as
plantas obtidas através das funções de transferência. As repostas ao
Apostila de Controle de Conversores Estáticos
PPGEEL
96
Modelagem de conversores em condução descontínua
degrau para casa situação também estão dentro do esperado para cada
planta.
5
Modelagem do conversor BOOST em condução contínua
[23]
5.1
INTRODUÇÃO
A crescente evolução das soluções eletrônicas, bem como, sua
viabilidade econômica e técnica vem aumentando e destacando a
aplicação de conversores de CC-CC em variados ramos de aplicação.
Neste trabalho é apresentado o modelamento do conversor Boost
em condução contínua para pequenos sinais, que se trata de um elevador
de tensão com relação não linear entre tensão de entrada e saída em
função do razão cíclica.
Este conversor é amplamente utilizado em circuitos de correção
de fator de potência, ou seja, esta modelagem tem grande aplicabilidade.
Desta forma, a busca por modelos e formas de controle deste conversor
segue a uma tendência de aprimoramento e evolução.
5.2
CONVERSOR BOOST
O conversor Boost trata-se de um elevador de tensão,
caracterizado por ter entrada em corrente e saída em tensão. Na Erro!
Fonte de referência não encontrada. é apresentada a configuração
básica do conversor, o qual em tese tem como menor valor de saída à
própria tensão de entrada. Este conversor é bem exposto e descrito na
referência [24].
O circuito consiste na aplicação de um interruptor S, um diodo D,
um indutor L, uma fonte constante E na entrada, um capacitor C
utilizado como filtro, além da carga representada pelo resistor R,
demonstrado na Fig. 5.1.
Fig. 5.1 - Circuito Boost
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
97
Este conversor pode operar no modo de operação contínuo ou
descontínuo, ou seja, a corrente no indutor pode ou não chegar à zero.
Neste trabalho será analisada apenas a operação do conversor em
modo contínuo (CCM), sendo assim, existem duas etapas de operação,
sendo: Na primeira etapa a chave S está conduzindo, o indutor L é
magnetizado e a fonte E fornece energia ao indutor. O capacitor C
previamente carregado fornece energia à carga R, conforme visualizado
na Erro! Fonte de referência não encontrada.. Na segunda etapa a
chave S está bloqueada, o diodo D entra em condução, a fonte E e o
indutor L fornecem energia à saída, conforme visualizado na Fig. 5.3.
Como consequência, a tensão na carga R aumenta.
Fig. 5.2 - Primeira etapa de operação conversor Boost
Fig. 5.3 - Segunda etapa de operação conversor Boost
As formas de onda dos componentes principais do conversor são
apresentadas na Fig. 5.4.
Apostila de Controle de Conversores Estáticos
PPGEEL
98
Modelagem de conversores em condução descontínua
Fig. 5.4 - Formas de onda do conversor Boost
Para o cálculo do ganho do conversor em regime permanente, a
tensão média no indutor deve ser zero, conforme a equação (10.1).
Calculando o valor médio de vL chega-se na equação (10.2), que
demonstra a relação do ganho do conversor com a razão cíclica D.
vL =
1
T
(1− D )T
D T

 ∫ E dt + ∫ ( E − Vo ) dt  = 0
 0

DT
Apostila de Controle de Conversores Estáticos
(10.1)
PPGEEL
Modelagem de conversores em condução descontínua
Vo
1
=
E 1− D
5.3
99
(10.2)
MODELO CONVERSOR
Devido ao fato deste conversor possuir a característica de uma
fonte de corrente na entrada (indutor L em série com a fonte de tensão
E), o modelamento é realizado conforme o procedimento a seguir:
Realiza-se o cálculo da tensão média no indutor L e da corrente média
no capacitor C, depois é aplicado uma perturbação no sistema e isolado
os termos de 1º ordem. Ao final do processo, é aplicada a transformada
de Laplace nas equações resultantes, visando à obtenção dos modelos de
tensão e corrente de saída pela razão cíclica e do modelo de tensão de
saída pela corrente de saída.
5.3.1
Etapas de Operação BOOST condução contínua
Com o interruptor fechado, a somatória das tensões é apresentada
em (10.3), além disso, vale lembrar a equação de corrente dos
capacitores (10.4).
− E + vL = 0
(10.3)
iC (t ) =
−v(t )
R
(10.4)
Na segunda etapa de operação, obtém-se também a malha de
tensão (10.5), bem como a malha de corrente (10.6), que culminam em
(10.7).
− E + vL ( t ) + v ( t ) = 0
(10.5)
iL ( t ) = iC ( t ) + iR (t )
(10.6)
v(t )
R
(10.7)
iC ( t ) = iL ( t ) −
Obtêm-se os valores médios para as tensões do indutor (vLmed ) , e
corrente do capacitor (iCmed ) , as quais são calculadas e definidas em
(10.10) e (10.14):
Apostila de Controle de Conversores Estáticos
PPGEEL
100
Modelagem de conversores em condução descontínua
1
< vL ( t ) >Ts =
Ts
< vL ( t ) >Ts =
< vL ( t ) >Ts =
1
Ts
t +Ts
∫ δ dδ
(10.8)
t
t +Tc
∫
Ed δ +
t
t +Ts
1
Ts
∫ ( E − v(t ) ) d δ
(10.9)
t
1
1
ETc + ( E − v (t ) )(Ts − Tc )
Ts
Ts
(10.10)
Lembrando que Tc equivale à razão cíclica multiplicada pelo
período DTS , e seu complemento é 1-D além da equação de tensão para
indutores (10.11). Com todas estas considerações obtém-se (10.12).
d

< vL ( t ) >Ts = L  iL (t ) 
 dt

(10.11)
d

L  iL (t )  = E − v ( t ) (1 − d ( t ))
 dt

(10.12)
d

< ic ( t ) >Ts = C  vc (t ) 
 dt

(10.13)
Utilizando a mesma análise para o cálculo da corrente no
capacitor, manipulando (10.13) chega-se a (10.16):
< ic ( t ) >Ts =
1
Ts
t + Ts
∫
t
−v (t )
1
dδ +
R
Ts
t + Ts
∫
t
v (t ) 

 iL ( t ) +
 dδ
R 

(10.14)
v (t )
d
 v ( t ) d (t )
C  vc (t )  =
+ iL ( t ) (1 − d ( t ) ) −
(1 − d ( t ))
R
R
 dt

(10.15)
v (t )
d

C  vc (t )  = iL ( t ) (1 − d ( t ) ) −
R
 dt

(10.16)
5.3.2
Modelagem de pequenos sinais
Neste desenvolvimento optou-se por utilizar a abordagem de
pequenos sinais, ou seja, pequenas variações no sistema com o intuito de
avaliar seu comportamento, principalmente sua saída diante de tais
perturbações. As grandezas abordadas são (10.17) a (10.20).
d (t ) = D + d ^ (t )
D ≫| d ^ |
Apostila de Controle de Conversores Estáticos
(10.17)
PPGEEL
Modelagem de conversores em condução descontínua
iL ( t ) = I L + iL ^ ( t )
I L ≫| iL ^ |
101
(10.18)
E ( t ) = E + e^ ( t )
E ≫| e ^ |
(10.19)
v (t ) = V + v^ (t )
V ≫| v ^ |
(10.20)
Aplicando perturbações nas equações (10.12) e (10.16), chega-se
a (10.23) e (10.26).
d
d

L  I + iL ^ ( t ))  = E + e ^ ( t ) − (V + v ^ ( t ) ) 1 − ( D + d ^ ( t ) ) 
dt
 dt

(10.21)
d
d

L  I + iL ^ ( t ))  = E + e^ ( t ) − V + V D + V d ^ ( t ) − v ^ ( t ) +
dt
 dt

^
^
^
+v ( t ) D + v ( t ) d ( t )
(10.22)
d
d

L  I + iL ^ ( t ))  = E − V + V D + e ^ ( t ) − v ^ ( t ) + V d ^ ( t ) +
dt
dt


+v^ ( t ) D + v^ (t ) d ^ ( t )
(10.23)
^
d
d
 −V v ( t )
C  V + v^ (t )  =
−
+
dt
R
 dt
 R
+ ( I + iL ^ ) (− (V + v ^ ( t ) ) 1 − ( D + d ^ ( t ) ) 
(10.24)
^
d
d
 −V v ( t )
C  V + v ^ ( t ))  =
−
+ I − I D − I d ^ (t ) +
dt
dt
R
R


+ iL ^ − iL ^ D − iL ^ d ^ ( t )
(10.25)
v^ (t )
d
d
 −V
C  V + v ^ ( t ))  =
+I −I D−
−
dt
R
 dt
 R
− I d ^ ( t ) + iL ^ − iL ^ D − iL ^ d ^ ( t )
(10.26)
Pode-se verificar a existência de termos constantes, que
representam o conversor em regime permanente, termos de primeira
ordem e termos de segunda ordem. Como foi previamente exposto, as
variações são muito pequenas em relação aos valores obtidos no ponto
de operação em análise. Com isso, os termos de segunda ordem serão
desconsiderados e assim, somente os termos de primeira ordem serão
avaliados, esta abordagem é feita e descrita em [25].
Apostila de Controle de Conversores Estáticos
PPGEEL
102
Modelagem de conversores em condução descontínua
5.3.2.1
Transformada de Laplace
A sequência da análise de pequenos sinais é feita aplicando-se a
transformada de Laplace nas equações (10.23) e (10.26). Considerando
apenas os termos de primeira ordem, chegando-se a (10.29) e (10.30).
d

L  iL ^ ( t ))  = e ^ ( t ) + V d ^ ( t ) − v ^ (t ) + v ^ ( t ) D
 dt

(10.27)
v^ (t )
d

C  v ^ ( t ))  = −
− I d ^ ( t ) + iL ^ − iL ^ D
dt
R


(10.28)
L s iL ( s ) = vg ( s ) + V d ( s ) − v ( s ) (1 − D)
(10.29)
−v ( s )
− I d ( s ) + iL ( s ) (1 − D)
R
Manipulando a equação (10.30) define-se (10.32).
C s v ( s) =
(10.30)
1

v ( s )  C s +  = − I d ( s ) + iL (1 − D )
R

(10.31)
− I d ( s ) + iL ( s ) (1 − D)
1
Cs+
R
(10.32)
v ( s) =
Substituindo (10.32) em
matemáticas obtém-se (10.38).
(10.29)
e
com
manipulações


 − I d ( s ) + iL ( s ) (1 − D) 
L s iL ( s ) = e ( s ) + V d ( s ) − 
 (1 − D )
1


Cs+

R

(10.33)


 − I d ( s ) + iL ( s ) (1 − D ) 
e ( s) +V d ( s) − 
 (1 − D)
1


Cs+

R

iL ( s ) =
Ls
(10.34)
Avaliando apenas a influência da variação na razão cíclica sobre
a corrente no indutor, logo, e(s) =0, define-se (10.35):
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua


 − I d ( s ) + iL ( s ) (1 − D ) 
V d ( s) − 
 (1 − D)
1


Cs+

R

iL ( s ) =
Ls
103
(10.35)
1
2

Vd ( s )  Cs +  − iL ( s )(1 − D ) + d ( s ) I (1 − D )
R

iL ( s ) =
1

Ls  Cs + 
R

(10.36)
 
1
1
2

iL ( s )  Ls  Cs +  + (1 − D )  = Vd ( s )  Cs +  + d ( s ) I (1 − D )
R
R






(10.37)
 
1

d ( s ) V  C s +  + I (1 − D ) 
R

 

iL ( s ) =
1
2

L s C s +  + (1 − D )
R

(10.38)
Levando-se em consideração as equações básicas do conversor
Boost (10.39) a (10.42), e chega-se (10.44).
1
V
=
E (1 − D )
(10.39)
E = V (1 − D)
(10.40)
Considerando a potência de entrada igual à de saída, chega-se
(10.42):
EI =
V2
R
I (1 − D ) =
(10.41)
V
R
(10.42)
1 V

V  Cs +  +
R R

=
1
2
d (s)

Ls  Cs +  + (1 − D )
R


(10.43)
iL ( s )
V R C s + 2V
=
d ( s ) R L C s 2 + L s + R(1 − D) 2
(10.44)
iL ( s )
Apostila de Controle de Conversores Estáticos
PPGEEL
104
Modelagem de conversores em condução descontínua
Colocando no formato padrão, chega-se (10.45).
V
2V
s+
iL ( s )
L
R
LC
=
(10.45)
d (s)
s
(1
− D)2
2
s +
+
RC
LC
Agora, fazendo as mesmas substituições para a tensão do
capacitor, juntamente com a equação (10.46), culmina na equação
(10.48).
iL ( s ) =
e ( s ) + V d ( s ) − v ( s ) (1 − D)
C s v ( s) =
v ( s) =
(10.46)
Ls
−v ( s )
− I d ( s ) + iL ( s ) (1 − D)
R
d ( s ) V R (1 − D ) − L I R s 
L C R s 2 + L s + R (1 − D )2
+
(10.47)
e ( s )(1 − D ) R
L C R s 2 + L s + R (1 − D )2
(10.48)
Avaliando apenas a influência da variação na razão cíclica sobre
a tensão do capacitor, logo, e(s) =0, chega-se à (10.49).
V R (1 − D ) − L I R s 
v( s )
= 
d ( s ) L C R s 2 + L s + R (1 − D) 2
(10.49)
Colocando no formato padrão, chega-se (10.50).
 −I  V
s  +
(1 − D )
v( s )
C  LC

=
2
d (s)
(1 − D )
s
s2 +
+
RC
LC
(10.50)
A planta de tensão de saída pela corrente do indutor tem grande
importância nos controles de conversores Boost aplicados na correção
do fator de potência, por exemplo, em retificadores de tensão.
Nos conversores de tipo Boost a corrente média de carga ( I o ) é a
mesma do diodo ( I D ) . Esta por sua vez, pode ser escrita em função da
corrente do indutor ( I L ) , equivalente a corrente média da entrada, fato
apresentado em (10.51). Esta modelagem é apresentada na Fig. 5.5.
I o = (1 − D ) I L
Apostila de Controle de Conversores Estáticos
(10.51)
PPGEEL
Modelagem de conversores em condução descontínua
105
Fig. 5.5 - Circuito equivalente Boost para Relação Tensão Corrente.
A corrente IDmd é igual à somatória da corrente do capacitor C e
carga R, conforme (10.52).
(1 − D ) I L = C
dV V
+
dt R
(10.52)
Aplicando Laplace e manipulando a equação (10.52) chega-se a
função de transferência (10.53).
V ( s ) R (1 − D )
=
I L ( s ) RCs + 1
(10.53)
Colocando no formato padrão, chega-se (10.54).
V (s)
IL ( s)
(1 − D )
=
5.3.3
5.3.3.1
C
s+
1
RC
(10.54)
Simulações
Especificações e definições da simulação
A simulação do circuito foi executada no software PSIM, onde se
avaliou a tensão de saída e corrente do indutor. A simulação dos
modelos da planta também foram feiras no Simulink com o intuito de
facilitar a análise e reduzir o tempo de simulação, ou seja, têm-se a saída
do circuito elétrico os valores de tensão e corrente, bem como, a saída
das funções transferência, onde os dois resultados são comparados.
V2
Ro = o = 400Ω
Po
Apostila de Controle de Conversores Estáticos
PPGEEL
106
Modelagem de conversores em condução descontínua
Vc = 400V − Tensão de Saída
f s = 70 KHz − Frequência de chaveamento
L = 4mH − Indutor
C = 1uF − Capacitor de filtro de saída
Po = 400W − Potência de saída
Através da equação (10.2), D = 0.5 .
A carga e corrente de saída são calculadas para atingir a potência
e tensão estabelecidas.
Ro =
Io =
Vo 2
= 400Ω
Po
Po
= 1A
Vo
(10.55)
(10.56)
Na Fig. 5.6 tem-se o circuito das simulações no PSIM.
Fig. 5.6 - Circuito Boost com Modelo simulado
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
5.3.3.2
107
Resultados
Nas Fig. 5.7 e Fig. 5.8 têm-se os resultados para as plantas de
corrente ( I L ) e tensão ( Vc ) para as diferentes variações de D (1% a 9%).
Em vermelho e verde tem-se os resultados do circuito e em azul o
resultado da função transferência.
Corrente
+/1%
+/2%
+/3%
+/4%
Apostila de Controle de Conversores Estáticos
PPGEEL
108
Modelagem de conversores em condução descontínua
+/5%
+/6%
+/7%
+/8%
+/9%
Fig. 5.7 - Resultados de Simulação do Conversor Boost para plantas de
corrente pela razão cíclica.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
109
Tensão
+/1%
+/2%
+/3%
+/4%
+/5%
Apostila de Controle de Conversores Estáticos
PPGEEL
110
Modelagem de conversores em condução descontínua
+/6%
+/7%
+/8%
+/9%
Fig. 5.8 - Resultados de Simulação do Conversor Boost para plantas de
tensão pela razão cíclica.
Pode-se verificar que ambas as plantas possuem características
semelhantes quanto à variação da razão cíclica. Entretanto, a planta de
tensão apresenta maior sensibilidade a variações na razão cíclica, ou
seja, com variação de 4% já apresenta divergência significativa (visual)
entre a simulação do circuito e o modelo do conversor. Por outro lado,
na planta de corrente está variação passa a ser significativa em 6% de
variação na razão cíclica.
Com o intuito de verificar as características dos modelos que
justifique a diferença entre as dinâmicas das plantas, foram feitos os
diagramas de Bode para ambas as plantas conforme a Fig. 5.9 e a Fig.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
111
5.10
Fig. 5.9 - Diagrama de Bode plata de corrente.
Fig. 5.10 - Diagrama de Bode plata de tensão.
Apostila de Controle de Conversores Estáticos
PPGEEL
112
Modelagem de conversores em condução descontínua
Analisando a Fig. 5.9 e Fig. 5.10, ficam evidentes as diferenças
entes as plantas com relação a ganho e margem de fase. Desta forma,
fica claro que as plantas não terão a mesma dinâmica, ou seja, as
variações nas entradas irão gerar diferentes comportamentos para cada
planta.
Na sequência são apresentados os resultados do modelo da tensão
de saída pela corrente do indutor. Nas Fig. 5.11e Fig. 5.12 são
apresentados os resultados do modelo da tensão de saída pela corrente
do indutor, entretanto a variação feita equivale ao valor da corrente no
diodo D (10.51), variando a mesma em 10% e 50%.
+ID%
10%
50%
Fig. 5.11 – Resultado de Simulação do Conversor Boost para plantas de
tensão por corrente.
-ID%
10%
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
113
50%
Fig. 5.12 - Resultados de Simulação do Conversor Boost para plantas
de tensão por corrente.
O circuito apresenta comportamento de primeira ordem conforme
esperado, sendo assim, validado para uso nos circuitos de controle,
inclusive para grandes variações da corrente em questão ( I L ) .
5.4
Conclusão
Conforme esperado os modelos do conversor Boost apresentaram
respostas não lineares de acordo com a variação da razão cíclica. Ou
seja, quão maior a variação na razão cíclica, maior será o erro obtido
pelo modelo em relação ao circuito real. Sendo assim, estes modelos são
validos para pequenas variações na razão cíclica, característica já
esperada pelos equacionamentos propostos. Sendo assim, para a planta
de tensão a variação da razão cíclica na qual o modelo mantém
comportamento satisfatório é de 4% e na de corrente 6%. Por sua vez, a
planta de tensão de saída pela corrente do indutor apresentou resultados
condizentes com um sistema de primeira ordem (sem erro de regime
permanente), além de ser válidos para as malhas de controle de tais
conversores.
Apesar de não terem sidos observados casos onde a tensão de
saída, ou corrente no indutor passem ou sejam inferiores a zero no
momento do transitório (mudanças de carga, por exemplo). Caso
venham a ocorrer, no modelo não existirão limitações para valores
negativos, algo não aplicável no circuito real.
Outro fator relevante trata-se do ponto de operação analisado,
caso seja definido, por exemplo, uma razão cíclica nominal de 10%
(D=0,1), as variações da mesma poderão ser maior, visto que neste
ponto de operação existe uma maior linearidade entre tensão de saída
pela entrada em função da razão cíclica. Isto acarreta que o modelo terá
resposta mais fiel ao circuito quando operando com valores pequenos de
razão cíclica.
Apostila de Controle de Conversores Estáticos
PPGEEL
114
6
Modelagem de conversores em condução descontínua
Modelagem do conversor BUCK-BOOST em condução
contínua
[25] [22]
6.1 Introdução
Para controlar um conversor, é necessário saber qual é o seu
comportamento perante variações nas variáveis de entrada. As variáveis
de entrada consideradas para o conversor apresentado neste texto são a
razão cíclica e a tensão de entrada. Ao modificar alguma variável de
entrada, as variáveis de saída também modificarão. Para um sistema em
malha aberta, ao reduzir a tensão d entrada, é claro que a tensão de saída
reduzirá. Já se variar a razão cíclica, dependendo da topologia do
conversor, a afirmação feita anteriormente pode não ser verdade. Para
saber o comportamento do conversor perante a estas variações, é
necessário ter em mãos o seu modelo matemático.
Para extrair o modelo matemático do conversor existem diversas
técnicas, existem softwares que fazem o modelamento, e pode-se obter
este modelo na prática, fazendo uma varredura em frequência na
variável de entrada do conversor e ler a saída. Mas neste texto será
apresentado o método para modelar os conversores que operam em
condução contínua através de técnicas que analisam a tensão média no
indutor e a corrente média no capacitor, será obtido o modelo de um
conversor buck-boost, mas esta técnica pode ser utilizada em outros
conversores. Além desta técnica, é apresentada uma forma de obter um
modelo matemático a partir do circuito, fazendo a varredura em
frequência de uma variável de entrada utilizando o programa PSIM®.
Não será extraído o modelo matemático em si, ele será utilizado apenas
para comparar e validar os modelos encontrados a partir das técnicas de
tensão média no indutor e corrente média no capacitor, mas tendo do
diagrama de bode, para obter o modelo, basta fazer uma análise do
gráfico. Ao final os modelos obtidos serão comparados e será mostrado
que as técnicas funcionam bem.
6.2
Conversor buck-boost
O conversor buck-boost opera como elevador e abaixador de
tensão, dependendo da razão cíclica. Uma característica deste conversor
é que ele não transfere energia diretamente para a saída. Na etapa de
operação onde o interruptor encontra-se fechado a energia é armazenada
no indutor. Na etapa onde o interruptor está aberto, a fonte de entrada é
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
115
desconectada do circuito e o indutor descarrega a energia na saída. A
figura a seguir mostra o circuito de potência do conversor buck-boost.
S
D
+
vg (t )
+
L
−
C
v(t )
R
−
Fig. 6.1 - Circuito de potência do conversor buck-boost
A figura a seguir mostra os estados do interruptor, quanto está em
nível lógico alto, o interruptor está fechado, em nível lógico baixo, o
interruptor abre.
S
1ª Etapa
2ª Etapa
DTs
Ts
t
Fig. 6.2 - Estados do interruptor: Nível lógico alto o interruptor está
fechado; Nível lógico baixo, o interruptor está aberto
6.2.1
Primeira etapa
A figura a seguir mostra o funcionamento do conversor na
primeira etapa de operação. O indutor armazena a energia da entrada e a
saída é alimentada pelo capacitor.
Apostila de Controle de Conversores Estáticos
PPGEEL
116
Modelagem de conversores em condução descontínua
iL (t )
+
vg (t )
−
S
+
vL (t ) L
−
−
−
vC (t )
+
i C (t )
vR (t )
+
+
v(t )
−
i R (t )
Fig. 6.3 - Funcionamento do conversor na primeira etapa de operação:
chave fechada.
Pela figura é possível verificar que a tensão de saída tem a
polarização invertida em relação ao capacitor de saída. A seguir são
apresentadas as relações básicas para corrente e tensão em indutores
capacitores e resistores.
v L (t ) = L
iC (t ) =
iR (t ) =
diL (t )
dt
dvC (t )
dt
vR (t )
R
(11.1)
(11.2)
(11.3)
A seguir são apresentadas as equações do conversor para esta
primeira etapa de operação. Fazendo a análise das malhas do circuito:
vL (t ) = vg (t )
(11.4)
vC (t ) = vR (t )
(11.5)
v(t ) = −vC (t )
(11.6)
Fazendo análise dos nós do circuito:
iC (t ) = −iR (t )
(11.7)
iL (t ) = ig (t )
(11.8)
Estão apresentadas todas as equações de nó e malha para a
primeira etapa de operação, estas equações serão utilizadas
posteriormente.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
6.2.2
117
Segunda etapa
A figura a seguir mostra o funcionamento do conversor na
segunda etapa de operação. Nesta etapa o indutor descarrega a energia
no circuito.
+
vg (t )
−
+
vL (t ) L
D
vC (t )
−
−
−
vR (t )
+
iC (t )
iL (t )
+
+
v(t )
−
iR (t )
Fig. 6.4 - Funcionamento do circuito na segunda etapa de operação:
chave aberta
Nesta etapa a fonte de entrada do circuito está desconectada, a
corrente de entrada é zero. Fazendo análise das malhas do circuito:
v L (t ) = v (t )
(11.9)
vC (t ) = vR (t )
(11.10)
vC (t ) = −v(t )
(11.11)
Analisando os nós do circuito:
iC (t ) = iL (t ) − iR (t )
(11.12)
Estas equações serão utilizadas para encontrar o valor médio da
tensão no indutor e a corrente média no capacitor. Em regime
permanente tanto a tensão média no indutor quanto a corrente média no
indutor são nulas. Para isto acontecer, o valor da corrente no indutor em
um tempo t no início do período de comutação é igual ao valor da
corrente no indutor no tempo t + Ts , onde Ts é o período de comutação.
Ao sofrer uma pequena perturbação, a corrente no indutor varia mais
rápido que a frequência de comutação, mas esta mudança é prevista pela
sua tensão média. No capacitor ocorre este mesmo efeito, mas quem
varia acima da frequência de comutação é a tensão. A partir desta ideia
encontram-se as equações que determinam a tensão média no indutor e a
corrente média no capacitor em um período de comutação.
Apostila de Controle de Conversores Estáticos
PPGEEL
118
6.2.3
Modelagem de conversores em condução descontínua
Valores médios em um período de comutação
Para modelar o conversor, inicialmente faz-se necessário
encontrar as equações da corrente no capacitor e tensão média no
indutor para um período de chaveamento, ou seja, na primeira e na
segunda etapa.
Para a primeira etapa as equações de corrente no capacitor e
tensão no indutor são:
vg (t ) = vL (t ) = L
diL (t )
dt
iC (t ) = −iR (t ) = −
iC (t ) = C
(11.13)
vR (t )
R
dvC (t )
v (t )
=− R
dt
R
iC (t ) = −C
dv (t ) v(t )
=
dt
R
(11.14)
Na segunda etapa de operação, a equações de corrente no
capacitor e tensão indutor são:
v L (t ) = L
diL (t )
= v(t )
dt
(11.15)
iC (t ) = iL (t ) − iR (t ) = iL (t ) −
iC (t ) = C
vR (t )
R
dvC (t )
v (t )
= iL (t ) − R
dt
R
iC (t ) = −C
dv(t )
v (t )
= iL (t ) +
dt
R
(11.16)
Considerando um modelo para pequenos sinais, substituindo os
valores de v(t ) , vg (t ) e iL (t ) por v(t ) T , vg (t ) T e iL (t ) T , que
s
s
s
correspondem aos valores médios em um período de comutação. As
equações para a primeira etapa são:
v L (t ) = L
diL (t )
= v g (t )
dt
Ts
Apostila de Controle de Conversores Estáticos
(11.17)
PPGEEL
Modelagem de conversores em condução descontínua
iC (t ) = −C
v (t )
dv(t )
=
dt
R
119
Ts
(11.18)
As equações para a segunda etapa são:
v L (t ) = L
diL (t )
= v(t )
dt
iC (t ) = −C
(11.19)
Ts
dv(t )
= iL (t )
dt
+
Ts
v(t )
Ts
(11.20)
R
Em um período de comutação, as equações ficam:
 vg (t ) , 0 < t ≤ d (t )Ts

Ts
v L (t ) = 
 v(t ) Ts , d (t )Ts < t ≤ Ts
 v(t )


iC (t ) =  R

 iL (t )

6.2.3.1
Ts
Ts
0 < t ≤ d (t )Ts
,
+
(11.21)
v(t )
Ts
R
, d (t )Ts < t ≤ Ts
(11.22)
Tensão média no indutor
A tensão média no indutor em um período de comutação é dada
pela seguinte expressão:
vL
Ts
=
1
Ts
∫
t + Ts
t
vL (τ )dτ
(11.23)
Substituindo a equação (11.21) em (11.23).
vL
Ts
=
1
Ts
∫
t + d ( t )Ts
t
vg (τ )
Ts
dτ +
1
Ts
∫
t + Ts
t + d ( t )Ts
v(τ )
Ts
dτ
É importante lembrar que os valores
(11.24)
vg (t )
Ts
e
v(t )
Ts
são
constantes em um período de comutação, portanto são considerados
valores constantes na integral, isto vale para iL (t ) T que será utilizada
s
no próximo item.
Apostila de Controle de Conversores Estáticos
PPGEEL
120
vL
Ts
vL
Ts
L
Modelagem de conversores em condução descontínua
=
=
d
iL
dt
1
vg (τ )
Ts
1
v g (t )
Ts
Ts
Ts
Ts
= vg (t )
τ
t + d ( t )Ts
t
d (t )Ts +
Ts
+
1
v(τ )
Ts
1
v(t )
Ts
d (t ) + v(t )
Ts
Ts
Ts
τ
t + Ts
t + d ( t )Ts
Ts [1 − d (t )]
[1 − d (t )]
(11.25)
Atribuindo:
[1 − d (t )] = d '(t )
(11.26)
A equação (11.25) fica:
L
d
iL
dt
Ts
= vg (t )
Ts
d (t ) + v(t )
Ts
d '(t )
(11.27)
d
Nota-se que na equação (11.27) o termo L
iL
dt
Ts
é referente à
tensão média do indutor em um período completo de comutação,
di (t )
das equações (11.17) e (11.19), onde este
diferente do termo L L
dt
termo se refere a apenas uma etapa de operação.
6.2.4
Corrente média no capacitor
A corrente média no capacitor em um período de comutação é
dada por:
iC
Ts
=
1
Ts
∫
t + Ts
t
iC (τ )dτ
(11.28)
Substituindo a equação (11.22) em (11.28):
iC
Ts
=
1
Ts
∫
t + d ( t )Ts
t
v(τ )
R
Ts
dτ +
1
Ts
∫
t + Ts
t + d ( t )Ts

 iL (τ )

Apostila de Controle de Conversores Estáticos
Ts
+
v (τ )
R
Ts

 dτ

(11.29)
PPGEEL
Modelagem de conversores em condução descontínua
iC
Ts
iC
Ts
iC
Ts
−C
−C
1 v(τ )
=
Ts
R
=
=
v(t )
dt
d v(t )
dt
Ts
dt
6.2.5
Ts
R
d v(t )
d v
C
1 v(t )
Ts
R
Ts
Ts
=
t + d ( t )Ts
Ts
τ
t
Ts
d (t )Ts +
1
+  iL (τ )
Ts 

1
 iL (t )
Ts 

d (t ) + iL (t )
v(t )
R
= iL (t )
= − iL (t )
Ts
Ts
Ts
Ts
+
[1 − d (t )] +
d (t ) + iL (t )
[1 − d (t )] +
d '(t ) −
Ts
Ts
v(t )
Ts
+
v(τ )
R
v(t )
Ts
R
v(t )
Ts
R
[1 − d (t )] +
v(t )
Ts

τ

121
t + Ts
t + d ( t )Ts

 Ts [1 − d (t ) ]

[1 − d (t )]
v(t )
R
Ts
−
v(t )
R
Ts
d (t )
Ts
R
Ts
R
(11.30)
Perturbações
Utilizando as equações (11.27) e (11.30), aplicam-se perturbações
nas variáveis de entrada, ou seja, na tensão de entrada e na razão cíclica.
Estas perturbações são muito menores que o valor médio da variável no
ponto de operação.
vg (t )
Ts
= Vg + vˆg (t )
d (t ) = D + dˆ (t )
Vg >> vˆg (t )
D >> dˆ (t )
(11.31)
Como em algumas equações usou o termo d '(t ) , vale a pena
verificar o efeito das perturbações nesta variável, visto que isto
simplifica a visualização e a manipulação das equações.
d '(t ) = 1 − d (t )
Aplicando a perturbação:
d '(t ) = 1 − D − dˆ (t )
d '(t ) = D '− dˆ (t )
Ao aplicar estar perturbações na entrada, a saída também é
perturbada. Os sinais que aparecem na saída são:
Apostila de Controle de Conversores Estáticos
PPGEEL
122
iL
v
Modelagem de conversores em condução descontínua
= I L + iˆL (t )
Ts
I L >> iˆ(t )
= V + vˆ(t )
Ts
(11.32)
V >> vˆ(t )
As equações (11.27) e (11.30) ficam:
L
C
(
(
)
)
(
d
I L + iˆL (t ) = (Vg + vˆg (t ) ) D + dˆ (t ) + (V + vˆ(t ) ) D '− dˆ (t )
dt
(
d
(V + vˆ(t ) ) = − I L + iˆL (t )
dt
)
) ( D '− dˆ (t ) ) − V +Rv t )
ˆ(
(11.33)
(11.34)
O próximo objetivo é manipular as duas equações até obter uma
forma mais simples.
Fazendo a manipulação na equação (11.33):
(
)
(
)
(
d
I L + iˆL (t ) = (Vg + vˆg (t ) ) D + dˆ (t ) + (V + vˆ ) (t ) D '− dˆ (t )
dt
d
d
L I L + L iˆL (t ) = Vg D + vˆg (t ) D + Vg dˆ (t ) + vˆg (t )dˆ (t ) +
dt
dt
+VD '− Vdˆ (t ) + vˆ(t ) D '− vˆ(t )dˆ (t )
L
)
(11.35)
d ˆ
iL (t ) = Vg D + vˆg (t ) D + Vg dˆ (t ) + vˆg dˆ (t ) + VD '−
dt
−Vdˆ (t ) + vˆ(t ) D '− vˆ(t )dˆ (t )
0+ L
L
d ˆ
iL (t ) =  DVg + VD ' +  Dvˆg (t ) + D ' vˆ(t ) + (Vg − V ) dˆ (t )  +


dt
Constante
1ª Ordem
1ª Ordem
+ ( vˆg (t ) − vˆ(t ) ) dˆ (t ) 


(11.36)
2ª Ordem
A equação (11.36) mostra que ao aplicar perturbações, aparecem
termos constantes, termos lineares ou de primeira ordem e termos não
lineares ou de segunda ordem.
O mesmo será feito para a equação (11.34)
d
V + vˆ(t )
C (V + vˆ(t ) ) = − ( I L + iˆL (t ) ) D '− dˆ (t ) −
dt
R
(
)
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
)(
123
)
d
V + vˆ(t )
(V + vˆ(t ) ) = − I L + iˆL (t ) D '− dˆ (t ) −
dt
R
d
d
V vˆ(t )
(11.37)
C V + C vˆ(t ) = − I L D '− I L dˆ (t ) + iˆL (t ) D '− iˆL (t )dˆ (t ) − −
dt
dt
R
R
d
V vˆ(t )
0 + C vˆ(t ) = − I L D '+ I L dˆ (t ) − iˆL (t ) D '+ iˆL (t )dˆ (t ) − −
dt
R
R
(
C
(
)
V  ˆ
1
 d
 
 ˆ
ˆ 
ˆ
C dt vˆ(t )  =  − I L D '− R  +  I L d (t ) − D ' iL v − R vˆ(t )  + iL (t )d (t ) 

 
 

1ª Ordem
Constante
1ª Ordem
(11.38)
2ª Ordem
O objetivo destas contas é encontrar os modelos do conversor
buck-boost. Estes modelos representam matematicamente como as
saídas do conversor se comportam perante à variações nas entradas. Foi
visto anteriormente que as variáveis de entrada são a tensão de entrada e
a razão cíclica. Portanto buscam-se os modelos que mostram o
comportamento da corrente ou tensão com variação da tensão de entrada
ou variação da razão cíclica. É interessante observar que nas equações
(11.36) e (11.38) os termos de segunda ordem são apenas os que têm
influência da razão cíclica. Portanto uma planta que não dependa da
razão cíclica será de primeira ordem sem ser necessário linearizá-la. Não
faz sentido obter a planta da variação da razão cíclica perante uma
variação na tensão de entrada ou vice versa, pois as duas são variáveis
de entrada.
Em resumo, as plantas que se busca são:
v( s)
Gv( s ) =
d (s)
i (s)
Gi ( s ) = L
d (s)
i (s)
Givg ( s ) = L
vg ( s )
Gvvg ( s ) =
v(s)
vg ( s )
Apostila de Controle de Conversores Estáticos
PPGEEL
124
Modelagem de conversores em condução descontínua
6.2.6
Termos constantes
Os termos constantes das equações (11.36) e (11.38) mostram o
comportamento do conversor em regime permanente. Estas equações
são interessantes para obter uma função transferência mais enxuta.
6.2.6.1
Ganho estático
O ganho estático do conversor é a relação da tensão de saída em
função da tensão de entrada. Utilizando a equação (11.36) e comparando
apenas os termos constantes:
DVg + VD ' = 0
(11.39)
V
D
=−
Vg
D'
6.2.6.2
(11.40)
Corrente no indutor
Através da equação (11.38) é possível verificar como a corrente
do indutor se comporta em regime permanente.
− I L D '−
IL = −
6.2.7
V
=0
R
V
D'R
(11.41)
(11.42)
Transformada de Laplace
Com as equações do conversor e com o objetivo, basta apenas
resolver as equações diferenciais do conversor. A ferramenta
matemática utilizada para resolver será a transformada de Laplace.
Porém as equações (11.36) e (11.38) possuem termos de segunda ordem,
o que torna o sistema não linear. Mas foi considerado que as
perturbações são muito menores que valor médio do ponto de operação,
portanto estes termos de segunda ordem podem ser desprezados devido
ao fato de que não apesentem grande contribuição no funcionamento do
sistema. É importante lembrar que se as perturbações forem maiores, a
planta não representará corretamente o funcionamento do sistema.
Aplicando a transformada de Laplace nos termos de primeira
ordem das equações (11.36) e (11.38).
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
125
d ˆ
iL (t ) = Dvˆg (t ) + D ' vˆ(t ) + (Vg − V ) dˆ (t )
dt
(11.43)
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s ) + (Vg − V ) d ( s )
(11.44)
L
C
d
1
vˆ(t ) = I L dˆ (t ) − D ' iˆL (t ) − vˆ(t )
dt
R
(11.45)
1
v( s)
(11.46)
R
As equações (11.44) e (11.46) representam as funções do
conversor no domínio da frequência e serão repedidas, pois se tratam
das equações mais importantes para encontrar o modelo do conversor.
Cs ⋅ v( s ) = I L ⋅ d ( s ) − D ' iL ( s ) −
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s ) + (Vg − V ) d ( s )
(11.44)
1
v( s)
(11.46)
R
Para encontrar os modelos do conversor basta manipulá-las de
acordo com as necessidades.
Cs ⋅ v( s ) = I L ⋅ d ( s ) − D ' iL ( s ) −
6.2.8
Plantas do conversor
Neste item são aplicadas as equações (11.44) e (11.46) para obter
as plantas do conversor. Para isto basta apenas manipulá-las de forma
que se obtenham as variáveis necessárias. As plantas não serão
analisadas perante a duas variações de entrada, ou seja, variando a razão
cíclica e a tensão de entrada ao mesmo tempo. Portanto para as plantas
que dependem da razão cíclica, as variações da tensão de entrada serão
consideradas zero, apenas as variações, já o termo quiescente continuará
igual. E para as plantas onde se busca o comportamento do conversor
perante a variação da tensão de entrada, as variações na razão cíclica
serão consideradas zero.
6.2.8.1
Planta de tensão pela razão cíclica
Utilizando as equações:
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s ) + (Vg − V ) d ( s )
Cs ⋅ v( s ) = I L ⋅ d ( s ) − D ' iL ( s ) −
1
v( s)
R
Apostila de Controle de Conversores Estáticos
(11.44)
(11.46)
PPGEEL
126
Modelagem de conversores em condução descontínua
Considerando vg ( s) = 0 e para facilitar as contas, multiplica a
equação (11.44) por D ' R , e a equação (11.46) por − RLs .
D ' RLs ⋅ iL ( s ) = DD ' R ⋅ 0 + D '2 R ⋅ v( s ) + (Vg − V ) D ' R ⋅ d ( s )
(11.47)
− LCRs 2 ⋅ v( s ) = − I L LRs ⋅ d ( s ) + D ' LRs ⋅ iL ( s ) + Ls ⋅ v( s )
(11.48)
Somando as duas equações:
D ' RLs ⋅ iL ( s ) − LCRs 2 ⋅ v( s ) =
D '2 R ⋅ v( s ) + (Vg − V ) D ' R ⋅ d ( s )
− I L LRs ⋅ d ( s ) + D ' LRs ⋅ iL ( s ) + Ls ⋅ v( s )
− LCRs ⋅ v( s ) = D ' R ⋅ v ( s ) + Ls ⋅ v( s ) + (Vg − V ) D ' R ⋅ d ( s ) −
2
(11.49)
2
− I L LRs ⋅ d ( s ) − ( LCRs 2 + Ls + D '2 R ) v( s ) = (Vg − V ) D ' R − I L LRs  d ( s )
v( s ) I L LRs − (Vg − V ) D ' R
=
d (s)
LCRs 2 + Ls + D '2 R
(11.50)
A equação (11.50) representa a planta de tensão pela razão cíclica
do conversor buck-boost, porém utilizando os valores encontrados nas
equações (11.40) e (11.42)
V
D
=−
Vg
D'
Vg = −
D'
V
D
IL = −
V
D'R
Substituindo (11.42) e (11.51) em (11.50)
Apostila de Controle de Conversores Estáticos
(11.40)
(11.51)
(11.42)
PPGEEL
Modelagem de conversores em condução descontínua
v( s )
=
d (s)
v( s )
=
d (s)
v( s )
=
d (s)
−
−
−
127
V
 D'

LRs −  − V − V  D ' R
D'R
 D

LCRs 2 + Ls + D '2 R
V
 1− D

LRs −  −
V −V  D ' R
D'R
D


LCRs 2 + Ls + D '2 R
(11.52)
V
 V DV

LRs −  − +
−V  D ' R
D'R
 D D

LCRs 2 + Ls + D '2 R
V
D'R
−
LRs +
V
v( s )
D
R
D
'
=
d ( s ) LCRs 2 + Ls + D '2 R
Isolando o termo
(11.53)
V
na parte de cima da equação (11.53):
DD '
v( s )
V
DLs − D '2 R
=−
d (s)
DD ' LCRs 2 + Ls + D '2 R
(11.54)
A equação (11.54) representa a planta de tensão pela razão
cíclica.
6.2.8.2
Planta de Corrente Pela Razão Cíclica
Para facilitar o entendimento, as equações (11.44) e (11.46) serão
reapresentadas abaixo.
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s ) + (Vg − V ) d ( s )
Cs ⋅ v( s ) = I L ⋅ d ( s ) − D ' iL ( s ) −
1
v( s)
R
(11.44)
(11.46)
Como precisa eliminar a variável v( s) , a equação (11.46) será
reescrita da seguinte forma:
1

0 = I L ⋅ d ( s ) − D ' iL ( s ) −  + Cs  v( s )
R


0 = I L R ⋅ d ( s ) − RD ' iL ( s ) − (1 + RCs ) v( s )
Apostila de Controle de Conversores Estáticos
(11.55)
PPGEEL
128
Modelagem de conversores em condução descontínua
Considerando vg ( s) = 0 e para facilitar as contas, multiplica a
equação (11.44) por (1 + RCs ) , e a equação (11.55) por RD ' .
L (1 + RCs ) s ⋅ iL ( s ) = D ' (1 + RCs ) v( s ) + (Vg − V ) (1 + RCs ) d ( s )
(11.56)
1

0 = I L RD '⋅ d ( s ) − RD '2 iL ( s ) − RD '  + Cs  v( s )
R


(11.57)
Somando as duas equações:
L (1 + RCs ) s ⋅ iL ( s ) + 0 =
D ' (1 + RCs ) v( s ) + (Vg − V ) (1 + RCs ) d ( s )
+ I L RD '⋅ d ( s ) − RD '2 iL ( s ) − D ' (1 + RCs ) v( s )
L (1 + RCs ) s ⋅ iL ( s ) = (Vg − V ) (1 + RCs ) d ( s ) + I L RD '⋅ d ( s ) − RD '2 iL ( s )
(11.58)
L (1 + RCs ) s ⋅ iL ( s ) + RD ' iL ( s ) = (Vg − V ) (1 + RCs ) d ( s ) + I L RD '⋅ d ( s )
2
 RLCs 2 + Ls + RD '2  iL ( s ) = (Vg − V ) (1 + RCs ) + I L RD ' d ( s )


iL ( s ) (Vg − V ) (1 + RCs ) + I L RD '
(11.59)
=
d (s)
RLCs 2 + Ls + RD '2
A equação (11.59) representa a planta de corrente pela razão
cíclica do conversor buck-boost, mas serão utilizadas as substituições
usadas na planta de tensão.
D'
V
D
V
Vg = V −
D
Vg = −
V
D'R
Substituindo (11.42) e (11.61) em (11.59):
IL = −
Apostila de Controle de Conversores Estáticos
(11.60)
(11.42)
PPGEEL
Modelagem de conversores em condução descontínua
129
V
V


V − − V  (1 + RCs ) −
RD '

iL ( s ) 
D
RD '

=
d (s)
RLCs 2 + Ls + RD '2
 V V

− − RCs  − V
iL ( s )  D D

=
d ( s ) RLCs 2 + Ls + RD '2
(11.62)
V V
V
− − D − RCs
iL ( s )
D
= D D
d ( s ) RLCs 2 + Ls + RD '2
Isolando o termo −
V
:
D
iL ( s )
V
1 + D + RCs
=−
d (s)
D RLCs 2 + Ls + RD '2
(11.63)
A equação (11.63) representa a função transferência da planta
de corrente pela razão cíclica.
6.2.8.3
Planta de tensão de saída pela tensão de entrada
Para encontrar a planta de tensão de saída pela tensão de entrada,
é necessário considerar que variação na razão cíclica é zero. Como
mencionado anteriormente, esta planta é linear, portanto é válida para
perturbações maiores. As equações serão novamente apresentadas
abaixo.
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s ) + (Vg − V ) d ( s )
Cs ⋅ v( s ) = I L ⋅ d ( s ) − D ' iL ( s ) −
1
v( s)
R
(11.44)
(11.46)
Considerando d (t ) = 0 , as equações ficam:
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s )
(11.64)
0 = − RD ' iL ( s ) − (1 + RCs ) v( s )
(11.65)
Deve-se eliminar a variável da corrente de entrada, para isto,
multiplica a equação (11.64) por RD ' e a equação (11.65) por − Ls e
somam as duas:
Apostila de Controle de Conversores Estáticos
PPGEEL
130
Modelagem de conversores em condução descontínua
RD ' Ls ⋅ iL ( s ) = RD ' D ⋅ vg ( s ) + RD '2 v( s )
0 = LRD ' siL ( s ) + (1 + RCs ) Ls ⋅ v( s )
0 = RD ' D ⋅ vg ( s ) + RD '2 v( s ) + (1 + RCs ) Ls ⋅ v( s )
( RD ' + Ls + RLCs ) v( s) = − RD ' D ⋅ v
2
2
g
(s)
v( s)
− RD ' D
=
vg ( s ) RLCs 2 + Ls + RD '2
(11.66)
(11.67)
(11.68)
A equação (11.68) representa a função de transferência da planta
de tensão de saída pela tensão de entrada.
6.2.8.4
Planta de corrente no indutor pela tensão de entrada
Para encontrar a planta de corrente no indutor pela tensão de
entrada, são feitas as mesmas considerações usadas para a planta de
tensão de saída pela tensão de entrada. Utilizando as equações (11.64) e
(11.65)
Ls ⋅ iL ( s ) = D ⋅ vg ( s ) + D ' v( s )
(11.64)
0 = − RD ' iL ( s ) − (1 + RCs ) v( s )
(11.65)
Neste caso, é necessário eliminar a variável da tensão de saída,
para isto, multiplica a equação (11.64) por (1 + RCs ) e a equação
(11.65) por D ' :
Ls (1 + RCs ) ⋅ iL ( s ) = D (1 + RCs ) ⋅ vg ( s ) + D ' (1 + RCs ) v( s )
0 = − RD '2 iL ( s ) − (1 + RCs ) D ' v( s )
(11.69)
Somando as duas:
Ls (1 + RCs ) ⋅ iL ( s ) = D (1 + RCs ) ⋅ vg ( s ) − RD '2 iL ( s )
Ls (1 + RCs ) ⋅ iL ( s ) + RD '2 iL ( s ) = D (1 + RCs ) ⋅ vg ( s )
( RCs
2
(11.70)
+ Ls + RD '2 ) iL ( s ) = D (1 + RCs ) ⋅ vg ( s )
D (1 + RCs )
iL ( s )
=
vg ( s ) RCs 2 + Ls + RD '2
(11.71)
A equação(11.71) representa a função de transferência da planta
da corrente pela razão cíclica.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
6.3
131
Validação das plantas
No capítulo anterior, o conversor foi modelado. É importante
saber se as plantas encontradas são válidas. Para isso o software PSIM®
tem um recurso poderoso que permite extrair a função de transferência
de um circuito a partir de uma perturbação. Esta perturbação pode ser
alocada onde for conveniente. Nos casos apresentados no capítulo 6.2 as
perturbações devem ser inseridas na razão cíclica e na tensão de entrada.
Este recurso chamado AC Sweep, faz uma varredura em frequência e
retorna em um diagrama de bode da planta desejada. Para a verificação,
foi utilizado um conversor buck-boost com as seguintes especificações:
Tabela 2 - Especificações do conversor
Vg = 100 V
Tensão de entrada
V = −200 V
Tensão de saída
Potência de saída
Frequência de comutação
Razão cíclica
Capacitor de saída
Indutância
Resistência de carga
Po = 200 W
f s = 20 kHz
D = 0, 666
C = 20 µ F
L = 15 mH
R = 200 Ω
Estas especificações garantem ao conversor a operação em modo
de condução contínua, condição em que as plantas foram modeladas.
6.3.1
Parameter File
Para iniciar o uso do AC Sweep é necessário um circuito. Para
isto será utilizado um circuito do conversor buck-boost apresentado a
seguir.
Apostila de Controle de Conversores Estáticos
PPGEEL
132
Modelagem de conversores em condução descontínua
Fig. 6.5 - Circuito do conversor buck-boost
Nota-se que as variáveis estão denominadas com letras. Será
utilizado outro recurso do PSIM®, que é a utilização do recurso
Parameter File. Este recurso permita ao usuário a utilização de letras
para determinar variáveis e a utilização destas letras em fórmulas
matemáticas, uma função que facilita bastante a análise das funções
transferência. Para usar este recurso, deve atribuir uma letra ao valor do
componente, como mostra a figura a seguir.
Fig. 6.6 - Resistor do circuito com o valor R atribuído para resistência.
A figura mostra destacado o campo do componente onde deve
usar a letra. Este recurso permite atribuir letra a qualquer parâmetro que
pode ser setado circuito, mas neste caso o parâmetro de interesse é o
valor da resistência.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
133
Após todos os elementos do circuito estarem atribuídos, insere-se
no circuito o componente Parameter File localizado no menu:
Elements>Other>Parameter File. Como mostra a figura a seguir.
Fig. 6.7 - Localização do recurso Parameter File no menu Elements do
PSIM®.
Após clicar, basta inserir este componente em qualquer lugar do
circuito e dar dois cliques no mouse que aparecerá a seguinte janela:
Fig. 6.8 - Janela de configuração do Parameter File.
A caixa de texto Name serve apenas para dar o nome ao
componente Parameter File que foi inserido.
A caixa de texto File mostra o diretório e o nome do arquivo
onde os parâmetros estão salvos. Para este recurso funcionar, é
necessário que o arquivo esteja salvo. Atenção na hora de fazer cópias
Apostila de Controle de Conversores Estáticos
PPGEEL
134
Modelagem de conversores em condução descontínua
de circuitos, pois o arquivo salvo não muda quando copia de um circuito
para outro, mesmo que o circuito do PSIM® esteja em outro arquivo.
A caixa de texto abaixo do File é o lugar onde podem ser
atribuídos valores para as letras que foram usadas nos componentes. A
entrada de texto é igual à entrada de texto do MatLab® ,portanto as
entradas de texto podem ser copiadas para MatLab® e verificar os
resultados neste progama.
A seguir é apresentado o arquivo utilizado para este circuito.
Fig. 6.9 - Exemplo de entrada de texto utilizada no menu Parameter
File.
A figura a seguir mostra o menu File.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
135
Fig. 6.10 - Detalhes do menu File do componente Parameter File.
Neste menu estão as opções para salvar o arquivo no disco e abrir
um outro arquivo de texto existente no disco rígido do computador.
6.3.2
AC Sweep
Com os parâmetros digitados, é hora de usar o AC Sweep. Este
recurso é encontrado no menu Elements>Other>AC Sweep, como
mostra a figura a seguir.
Fig. 6.11 - Localização do elemento AC Sweep.
Insere o elemento em qualquer lugar do circuito e dá dois cliques
no mouse para acessar as suas configurações que estão apresentadas a
seguir.
Apostila de Controle de Conversores Estáticos
PPGEEL
136
Modelagem de conversores em condução descontínua
Fig. 6.12 - Janela de configurações do elemento AC Sweep
Esta janela de configurações apresenta as seguintes opções
Name: Nome do elemento, utilizado apenas para identificação do
elemento AC Sweep que foi inserido no circuito.
Start Frequency: Frequência inicial da varredura. Quanto mais
baixa a frequência, mais demorada fica a simulação, pois o programa faz
simulações para várias frequências até atingir regime permanente, e para
frequências menores é mais demorado para atingir regime permanente.
End Frequency: Frequência final da varredura. Não faz sentido
usa frequências superiores à frequência de chaveamento, pois o
conversor não responderá corretamente se aplicar frequências na razão
cíclica maiores que a frequência da portadora.
No of Points: Número de pontos do gráfico. Este é número de
simulações que o programa fará até atingir regime permanente. Quanto
mais números utilizar, mais resolução o gráfico terá, porém o tempo de
simulação aumenta.
Flag for Points: Distribuição dos pontos do gráfico. Pode-se
escolher duas opções:
0 – Os pontos são distribuídos em escala logarítmica no eixo da
frequência (opção padrão).
1 – Os pontos são distribuídos em escala linear.
Como os gráficos de bode são em escala logarítmica na
frequência, deve-se utilizar 0 nesta opção.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
137
Source Name: Nome da fonte de perturbação. Deve-se inserir
uma fonte senoidal onde deseja aplicar a perturbação. Nesta caixa de
texto insere o nome do elemento desta fonte.
Start Amplitude: Amplitude inicial da perturbação. Esta
amplitude deve ser pequena devido a não linearidade das plantas
linearizadas a partir de um ponto de operação.
End Amplitude: Amplitude final. Em altas frequências o ganho
da planta diminui, esta opção serve como compensação desta redução do
ganho da planta inserindo um valor maior de amplitude nesta opção.
Freq. for extra Points: Esta opção serve para inserir pontos extras
em algumas frequências. Serve para melhorar a resolução do gráfico em
pontos mais detalhados do gráfico, como em frequências de ressonância,
onde ocorre um sobressinal.
Depois de definidos os parâmetros do AC Sweep, falta indicar
qual é a tensão que deseja verificar com a aplicação da perturbação. Para
isto insere o elemento AC Sweep Probe localizado no menu
Elements>Other>Probes>AC Sweep Probe como mostra a figura a
seguir.
Fig. 6.13 - Localização do AC Sweep Probe no PSIM®.
O AC Sweep Probe é uma ponteira de tensão utilizada para
monitorar a tensão em algum ponto do circuito, para ler a corrente, deve
ser utilizado um sensor de corrente do PSIM® com ganho unitário.
Insere o AC Sweep Probe no ponto do circuito que deseja monitorar. Por
exemplo, se deseja ver a planta de tensão por razão cíclica, é necessário
aplicar uma fonte senoidal na razão cíclica e monitorar a tensão de
saída.
Apostila de Controle de Conversores Estáticos
PPGEEL
138
6.3.3
Modelagem de conversores em condução descontínua
s-domain Transfer Function
Para comparar de forma prática as plantas encontradas no item
6.2.8 com o modelo que o PSIM® gera para o circuito, uma opção que o
software fornece é o elemento s-domain Transfer Function, este bloco
retorna a resposta de um sinal que passa por uma função transferência
no domínio da frequência. Este bloco é encontrado no menu
Elements>Control>Other
Function
Blocks>s-domain
Transfer
Function.
Fig. 6.14 - - Localização do elemento s-domain Transfer Function
Insere este bloco em qualquer lugar do circuito. E dá dois cliques
no mouse para acessar as configurações.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
139
Fig. 6.15 - Janela de configurações do elemento s-domain Transfer
Function
A Fig. 6.15 mostra a janela de configurações do bloco e mostra
também o bloco inserido. Para este bloco funcionar, deve-se inserir um
sinal de entrada. A janela de configurações apresenta as seguintes
opções:
Name: Nome do bloco.
Order n: Ordem da função transferência.
Gain: Ganho do sistema. Este valor multiplicará a função
transferência.
Coeff. Bn..B0: Coeficientes do numerador. Nesta caixa de texto
insere os coeficientes do numerador da função transferência, iniciando
no coeficiente de maior grau para o de menor grau.
Coeff. Bn..B0: Coeficientes do denominador. Semelhante aos
coeficientes do numerador.
A seguir é apresentado o formato da função transferência que
insere no bloco.
G (s) = k
Bn ⋅ s n + ..B 2 ⋅ s 2 + B1 ⋅ s1 + B 0 ⋅ s 0
An ⋅ s n + .. A2 ⋅ s 2 + A1 ⋅ s1 + A0 ⋅ s 0
(11.72)
Onde k é o ganho e n é a ordem. O numerador e o denominador
devem ter a mesma ordem, ou seja, o mesmo número de termos, caso
apresentem ordens diferentes, o coeficiente que a função não possui
deve ser preenchido com o número 0.
Apostila de Controle de Conversores Estáticos
PPGEEL
140
Modelagem de conversores em condução descontínua
No próximo item será apresentado o exemplo detalhado
mostrando os passos e configurações para validar a planta de tensão pela
razão cíclica e corrente pela razão cíclica encontradas no item 6.2.8.
6.3.4
Validação da planta de tensão e corrente pela razão cíclica
Neste item serão mostrados detalhadamente os passos para
validar as funções transferência. No item 6.2.8 foi visto que as planta de
tensão e corrente pela razão cíclica são:
v( s )
V
DLs − D '2 R
=−
d (s)
DD ' LCRs 2 + Ls + D '2 R
(11.73)
iL ( s )
V
1 + D + RCs
=−
d (s)
D RLCs 2 + Ls + RD '2
(11.74)
A figura a seguir mostra o circuito implementado para realizar a
validação.
Fig. 6.16 - Circuito do conversor buck-boost usado para validar as
plantas de tensão por razão cíclica e corrente por razão cíclica.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
141
Para realizar a validação foi inserida uma fonte senoidal com o
nome de Perturbacao em série com a razão cíclica, com isto insere-se
uma perturbação na razão cíclica. Os blocos s-domain Transfer
Function recebem como sinal de entrada a razão cíclica. Na saída destes
blocos estão as ponteiras de tensão e AC Sweep Probe, que serão
mostradas nos gráficos. Para facilitar a comparação, foi modificado o
nome das ponteiras para GIDModelo para a planta de corrente e
GVDModelo para a planta de tensão. No circuito de potência foram
adicionadas ponteiras no sensor de corrente para ler a corrente no
indutor e na tensão de saída. A figura a seguir mostra as configurações
utilizadas no bloco s-domain Transfer Function.
Fig. 6.17 - Janelas de configuração do s-domain Transfer Function para
a planta de tensão e planta de corrente.
Nota-se que as plantas são de segunda ordem, e foram inseridos
letras nos parâmetros, que serão atribuídas no Parameter File. a figura a
seguir mostra as configurações do Parameter File.
Apostila de Controle de Conversores Estáticos
PPGEEL
142
Modelagem de conversores em condução descontínua
Fig. 6.18 - Atribuição de valores nas letras definidas como valores dos
elementos do circuito.
Pela figura acima é possível verificar a facilidade que este recurso
trás. Foram utilizadas contas matemáticas para definir os coeficientes
das plantas. Portanto se desejar verificar o circuito com valores
diferentes de algum elemento basta alterar este elemento, que tudo que
depende deste elemento terá seu valor alterado. Os coeficientes do
denominador são iguais para todas as plantas obtidas neste trabalho,
portanto não serão alterados. A figura a seguir mostra as configurações
do AC Sweep.
Fig. 6.19 - Configurações utilizadas no AC Sweep.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
143
O valor utilizado para a amplitude da perturbação é de 1% da
razão cíclica, este valor pode ser verificado no Parameter File.
Quando o bloco AC Sweep estiver no circuito, as ponteiras de
tensão não funcionarão, apenas as AC Sweep Probe apresentarão
resultado. Para verificar a resposta ao degrau, o AC Sweep deve ser
apagado do circuito. O gráfico gerado tem o módulo em 20 log(G ( s))
para o eixo do módulo e na fase, os valores são em graus. É importante
lembrar que se utilizar a portadora com amplitude diferente de 1 o
módulo terá este ganho adicionado no gráfico gerado do circuito, e os
gráficos não serão iguais. As figuras a seguir mostram os resultados
obtidos.
Fig. 6.20 - Comparação dos gráficos de tensão por razão cíclica gerada
a partir pelo bloco s-domain Transfer Function, e gerado pelo circuito
de potência.
A figura mostra que para frequências próximas a frequência de
comutação, a resposta do circuito começa a ser diferente do modelo
matemático. Mas isto não é problema, pois a frequência de cruzamento
utilizada para cálculos de controle é no máximo 25% da frequência de
comutação. Esta planta apresenta um zero no semi-plano direito isto não
causa instabilidade no sistema, no módulo o comportamento é o mesmo
que para um zero no semi-plano esquerdo, mas na fase, este zero tem o
comportamento de um polo, ou seja, a faze decresce 90º ao invés de
crescer 90º como seria o esperado para um zero.
Apostila de Controle de Conversores Estáticos
PPGEEL
144
Modelagem de conversores em condução descontínua
Fig. 6.21 - Comparação dos gráficos de corrente por razão cíclica
gerada a partir pelo bloco s-domain Transfer Function, e gerado pelo
circuito de potência.
A planta de corrente apresenta o comportamento esperado para
um sistema de segunda ordem com um zero no semi-plano esquerdo. O
módulo apresenta uma ressonância, e pode-se notar que o zero encontrase próximo da frequência de ressonância, pois o módulo inicia em faixa
plana e próximo à frequência de ressonância o gráfico cresce, mas logo
passa a decrescer 20dB/dec.
A figura a seguir mostra o problema de utilizar valores mais altos
para amplitude da perturbação. A figura a seguir mostra as funções
transferência com uma perturbação de 10% da razão cíclica.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
145
Fig. 6.22 - Plantas de tensão e corrente pela razão cíclica com uma
perturbação de 10% da razão cíclica.
A Fig. 6.22 mostra que para a amplitude deltaD de 10% utilizada
na perturbação, as plantas do modelo matemático apresentam diferenças
dos modelos obtidos do circuito.
6.3.5
Validação da planta de tensão e corrente pela tensão de
entrada
As plantas de tensão e corrente pela tensão de entrada são:
v( s)
− RD ' D
=
vg ( s ) RLCs 2 + Ls + RD '2
(11.75)
D (1 + RCs )
iL ( s )
=
vg ( s ) RCs 2 + Ls + RD '2
(11.76)
Para validar estas plantas, a perturbação será inserida na tensão
de entrada. Este modelo é linear, portanto a amplitude da perturbação
não tem a necessidade de ser pequena. A figura a seguir mostra o
circuito utilizado para validar estas plantas.
Apostila de Controle de Conversores Estáticos
PPGEEL
146
Modelagem de conversores em condução descontínua
Fig. 6.23 - Circuito utilizado para validar as plantas de corrente e
tensão pela tensão de entrada.
A perturbação foi retirada da razão cíclica e colocada em série
com a tensão de entrada. a figura a seguir mostra os parâmetros
utilizados no Parameter File.
Fig. 6.24 - Atribuições feitas no Parameter File.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
147
As figuras a seguir mostram os resultados obtidos para as plantas
do circuito e do modelo matemático.
Fig. 6.25 - Planta de tensão de saída pela tensão de entrada do modelo
matemático e do circuito.
Esta planta possui dois polos complexos, que geram uma
frequência de ressonância próximo a 100 Hz, que faz a planta decrescer
40dB/dec após a frequência de corte.
Fig. 6.26 - Planta de corrente no indutor pela corrente de entrada do
modelo matemático e do circuito.
Apostila de Controle de Conversores Estáticos
PPGEEL
148
Modelagem de conversores em condução descontínua
Esta planta apresenta um zero no semi-plano esquerdo próximo a
frequência de ressonância da planta que faz a planta decrescer 20dB/dec
após a frequência de corte.
A figura a seguir mostra as plantas com uma perturbação maior,
para verificar a linearidade das plantas.
Fig. 6.27 - Respostas das plantas para uma perturbação com amplitude
de 20% da tensão de entrada.
Foi inserida uma perturbação com amplitude alta para verificar a
linearidade. Mesmo com este valor de amplitude, os modelos
matemáticos representam a resposta do circuito.
Com estes gráficos, os modelos foram validados. Em alguns
casos pode-se fazer a verificação por resposta ao degrau. Mas este
método não é muito interessante em alguns casos, pois as plantas não
representam o comportamento da tensão ou corrente em regime
permanente. A seguir é mostrada a função transferência do modelo de
tensão pela razão cíclica.
v( s )
V
DLs − D '2 R
=−
d (s)
DD ' LCRs 2 + Ls + D '2 R
(11.77)
Utilizando o teorema do valor final, a resposta em regime
permanente para este circuito é:
v( s) s →0 = −
V
D'
(11.78)
Pode-se perceber que esta planta não representa a tensão de saída
em regime permanente. Porém podem-se utilizar operações matemáticas
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
149
para obter a resposta, mas isto afetará o comportamento do sistema em
regime transitório, o que torna a verificação por degrau inviável.
6.4 Conclusões
Este texto mostrou uma forma de obter o modelo matemático das
plantas do conversor buck-boost. O princípio de modelagem é a partir da
tensão média no indutor e da corrente média no capacitor, encontrando
as equações que determinam estes valores, basta apenas fazer
manipulação matemática e resolver sistema de equações diferenciais que
neste caso foi utilizada a transformada de Laplace que já retorna a
função no domínio da frequência. Os modelos da planta dependentes da
razão cíclica são para pequenas perturbações, pois se tratam de sistemas
não lineares, porém apresentaram um bom funcionamento para
amplitudes de perturbação de 1% da razão cíclica, para 10% o modelo
divergiu do modelo esperado, mas não precisa ser necessariamente
descartado. Mas é importante saber que estes modelos respondem desta
forma para pequenas variações na razão cíclica. Já os modelos
dependentes da tensão de entrada são lineares, portanto respondem bem
para uma faixa ampla de variação, sendo que o modelo respondeu bem
para uma perturbação com 20% da tensão de entrada. Outro ponto
examinado no texto a resposta ao degrau não é um método eficiente para
validar as plantas em alguns conversores, devido ao fato de que a planta
não represente corretamente a variável analisada em regime permanente
ou no regime transitório. Mas como o controle é projetado no domínio
da frequência, o método de validação apresentado é suficiente para
verificar se o conversor está sendo bem modelado ou não.
7
Modelagem do conversor BUCK-BOOST em condução
descontínua
[25] [26]
7.1 Introdução
Para o desenvolvimento do controle de conversores estáticos
precisamos obter os modelos dos mesmos para verificar qual tipo de
controlador adotar e sintonizá-los de forma adequada. Desta forma,
neste trabalho será demonstrado como obter os modelos de tensão e
corrente, bem como validá-los através da resposta ao degrau e resposta
em frequência.
Apostila de Controle de Conversores Estáticos
PPGEEL
150
Modelagem de conversores em condução descontínua
O conversor escolhido para obtenção dos modelos é o buck-boost
operando em modo de condução descontínua (MCD). Tradicionalmente
os conversores boost e buck-boost são projetados para operar em
condução descontínua na situação de plena carga. Além disso, todos os
conversores podem operar em condução descontínua para pequenas
cargas.
Para a obtenção dos modelos de conversores operando em
condução descontínua é necessário primeiramente o modelo médio das
chaves (transistor e diodo). Com este modelo, é linearizado o conversor
em um ponto de operação e aplicado uma pequena perturbação para
obter o modelo de pequenos sinais.
7.2 Modelo médio dos interruptores
O esquema do conversor buck-boost é ilustrado na Fig. 7.1. As
tensões e correntes nos terminais das chaves semicondutoras são
definidos conforme mostrado: v1 (t ) e i1 (t ) são as formas de onda no
transistor, enquanto v2 (t ) e i2 (t ) são as formas de onda no diodo.
Fig. 7.1 - Conversor buck-boost.
O modelo médio das chaves é obtido através dos valores médios
das tensões e correntes nos terminais dos mesmos. Com os valores
médios é possível derivar um circuito equivalente que será o modelo
médio das chaves.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
7.2.1
151
Determinação dos valores médios
Para a determinação dos valores médios precisamos inicialmente
analisar a operação do conversor buck-boost, traçar as formas de onda e
obter os valores médios nos terminais das chaves.
O conversor buck-boost em condução descontínua apresenta
três etapas de operação:
1ª etapa (0 < t ≤ t1): o transistor é fechado, o diodo é polarizado
reversamente e entra em bloqueio. O indutor carrega-se linearmente
através da fonte Vg enquanto o capacitor e a carga ficam desconectados
da fonte Vg.
2ª etapa (t1 < t ≤ t2): o transistor é aberto, o diodo é polarizado
diretamente e entra em condução. O indutor transfere energia para o
capacitor e para a carga enquanto a fonte Vg fica desconectada do
circuito.
3ª etapa (t2 < t ≤ t3): O transistor continua aberto e a energia do
indutor foi descarregada totalmente, sendo o diodo bloqueado. A carga é
alimentada apenas pela energia no capacitor.
A seguir são apresentados os circuitos equivalentes para cada etapa
de operação descrita anteriormente:
Apostila de Controle de Conversores Estáticos
PPGEEL
152
Modelagem de conversores em condução descontínua
v2
+
i1
T
−
+
D
Vg
L
C
R
C
R
V
−
(a)
+
v1
−
i2
+
D
T
Vg
L
V
−
(b)
+
v1
T
−
+
v2
−
+
D
Vg
C
R
V
−
(c)
Fig. 7.2 - Etapas de operação do conversor buck-boost: (a) 1ª etapa
para 0 < t ≤ t1, (b) 2ª etapa para t1 < t ≤ t2, (c) 3ª etapa para t2 < t ≤ t3.
As formas de onda nas chaves semicondutoras e no indutor são
mostrados a seguir:
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
153
Fig. 7.3 - Formas de onda de tensão e corrente nas chaves
semicondutoras e no indutor do conversor buck-boost em MCD .
A corrente no indutor inicia-se em zero e cresce com uma
inclinação de vg/L até atingir o pico em t1 dado pela seguinte equação:
i pk =
vg
d1Ts ,onde: t1 = d1Ts
L
Apostila de Controle de Conversores Estáticos
(12.1)
PPGEEL
154
Modelagem de conversores em condução descontínua
Obtidas as formas de onda, o próximo passo consiste em obter os
valores médios de v1 (t ) i1 (t ) , v2 (t ) i2 (t ) em termos das variáveis do
conversor (L, C, vg (t ) , d1 (t ) e d 2 (t ) ). Através das formas de onda
temos que o valor médio de v1 (t ) é:
v1 ( t )
(
= d1 ( t ) 0 + d 2 ( t ) vg ( t )
Ts
Ts
− v (t )
Ts
) + d (t ) v
3
g
( t ) Ts
(12.2)
Como d3 ( t ) = 1 − d1 ( t ) − d 2 ( t ) , temos que:
v1 ( t )
= (1 − d1 ( t ) ) vg ( t )
Ts
Ts
− d2 ( t ) v ( t )
Ts
(12.3)
Da mesma forma podemos obter a tensão média no diodo e chegar
na seguinte equação:
i2 ( t )
Ts
=
d12 ( t ) Ts v1 ( t )
(12.4)
2L
A corrente média na entrada obtemos através da integral no período
da forma de onda de corrente i1 (t ) , como segue:
i1 ( t )
Ts
=
1
Ts
t + Ts
q
∫ i ( t ) dt = T
1
1
(12.5)
s
t
Onde q1 é a área da corrente i1 (t ) durante o intervalo t1 dada pela
seguinte equação:
q1 =
t + Ts
1
∫ i ( t ) dt = 2 ( d T ) i
1
1 s
(12.6)
pk
t
Substituindo a equação (12.1) em (12.6), temos:
i1 ( t )
Ts
=
d12 ( t ) Ts
2L
vg ( t )
(12.7)
Ts
De forma similar obtemos a corrente no diodo i2 (t ) , conforme
abaixo:
i2 ( t )
Ts
=
1
Ts
t + Ts
q
∫ i ( t ) dt = T
2
2
t
(12.8)
s
Onde q2 é a área da corrente i2 (t ) durante o intervalo t2 dada pela
seguinte equação:
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
q2 =
155
t + Ts
1
∫ i ( t ) dt = 2 ( d T ) i
2
2 s
(12.9)
pk
t
Substituindo a equação (12.1) em (12.9), temos:
i2 ( t )
Ts
=
d1 ( t ) d 2 ( t ) Ts
vg ( t )
2L
(12.10)
Ts
As equações (12.3), (12.4), (12.7) e (12.10) representam os valores
médios nos terminais das chaves semicondutoras para o conversor buckboost operando em MCD. Contudo, temos ainda que expressar o
subintervalo d2 em termos de d1, que representa a razão cíclica do
conversor. Como a tensão média no indutor é zero durante um ciclo
completo do conversor, obtemos a seguinte equação:
vL ( t )
Ts
= d1 ( t ) vg ( t )
Ts
+ d2 ( t ) v ( t )
Ts
+ d3 ( t ) 0
(12.11)
Isolando d2, chegamos no seguinte:
d 2 ( t ) = − d1 ( t )
vg ( t )
v (t )
Ts
(12.12)
Ts
Substituindo a equação (12.12) nas equações (12.3), (12.4), (12.7) e
(12.10), obtemos as equações dos valores médios nos terminais das
chaves semicondutoras do conversor buck-boost em MCD que servirão
para construção dos circuitos equivalentes das chaves.
v1 ( t )
Ts
= vg ( t )
v2 ( t )
Ts
= − v (t )
i1 ( t )
i2 ( t )
7.2.2
Ts
Ts
=
=
d12 ( t ) Ts
2L
(12.13)
Ts
(12.14)
Ts
v1 ( t )
d12 ( t ) Ts v1 ( t )
2L
v2 ( t )
Ts
(12.15)
2
Ts
(12.16)
Ts
Construção do circuito equivalente
Como as equações (12.13) e (12.14) são independentes,
utilizaremos as equações (12.15) e (12.16) para a construção dos
circuitos equivalentes do transistor e do diodo. A equação (12.15)
Apostila de Controle de Conversores Estáticos
PPGEEL
156
Modelagem de conversores em condução descontínua
modela o transistor e nota-se que a corrente média na entrada i1 ( t )
proporcional a tensão média aplicada na entrada v1 ( t )
Ts
Ts
é
. Sendo assim,
o modelo médio do transistor obedece a lei de ohm da seguinte forma:
i1 ( t )
Ts
=
v1 ( t )
Ts
(12.17)
R e ( d1 )
Onde a resistência efetiva Re é:
R e ( d1 ) =
2L
d12 ( t ) Ts
(12.18)
O circuito equivalente do transistor é mostrado na Fig. 7.4 e
consiste em uma resistência.
Fig. 7.4 - Circuito equivalente do modelo médio do transistor.
v2 ( t )
i2 ( t )
Multiplicando ambos os lados da equação (12.16) por
obtemos o seguinte:
Ts
Ts
v2 ( t )
Ts
=
v1 ( t )
2
Ts
R e ( d1 )
A potência média
= p (t )
p (t )
Ts
Ts
(12.19)
, aparentemente é consumida pela
resistência Re. Contudo, pela equação (12.19), a potência média na
entrada (transistor) é transferida para a saída (diodo).
Este
comportamento é representado por uma fonte de potência dependente,
ilustrado na Fig. 7.5.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
157
Fig. 7.5 - Fonte dependente de potência: (a) esquema (b) i-v
característica.
A curva característica da fonte de potência é ilustrada na Fig. 7.5
e é simétrica com relação à tensão e corrente; consequentemente a
potência fornecida é constante. Similarmente a uma fonte de tensão, a
fonte de potência não pode ser curto circuitada nos seus terminais de
saída para não haver uma corrente infinita. De forma similar a uma fonte
de corrente, não pode em seus terminais de saída haver um circuito
aberto para a tensão não tender ao infinito. A fonte de potência deverá
ser conectada a uma carga capaz de absorver a potência p(t) e o ponto de
operação é definido como a interseção da carga e da característica i-v da
fonte de potência.
O modelo médio geral de grandes sinais para uma rede de duas
chaves em condução descontínua é ilustrado naFig. 7.6. Esta
configuração é conhecida como modelo de resistor sem perdas (LFR),
pois a energia que seria dissipada na resistência Re é transferida para a
saída através da fonte dependente de potência.
Fig. 7.6 - (a) rede genérica de duas chaves, e (b) correspondente modelo
médio das chaves em MCD: as formas de onda média no transistor
obedecem a lei de Ohm, enquanto as formas de onda média no diodo
como um fonte de potência dependente.
Apostila de Controle de Conversores Estáticos
PPGEEL
158
Modelagem de conversores em condução descontínua
A configuração do conversor buck-boost com o modelo de
resistor sem perdas é mostrado na Fig. 7.7.
Fig. 7.7 - Conversor buck-boost em MCD com o modelo de resistor sem
perdas.
O ganho estático do conversor buck-boost operando em MCD é
obtido através da análise do circuito da Fig. 7.7. Como a potência na
entrada é igual à potência na saída temos a seguinte relação:
vg ( t )
Ts
i1 ( t )
Ts
=−
v (t )
2
Ts
R
(12.20)
Substituindo a equação (12.17) em (12.20), temos:
vg ( t )
2
Ts
R e ( d1 )
=−
v (t )
2
Ts
R
(12.21)
Desta forma temos que o ganho estático do conversor em estudo
para MCD é:
M =
7.2.3
v (t )
vg ( t )
Ts
Ts
=−
R
R e ( d1 )
(12.22)
Modelo para pequenos sinais
O próximo passo é a construção do modelo do circuito
equivalente de pequenos sinais do conversor buck-boost operando em
modo de condução descontínua. No circuito equivalente para grandes
sinais da Fig. 7.7, o modelo médio das chaves é não linear.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
159
Fig. 7.8 - Modelos médios geral de duas chaves em um conversor
operando em MCD: (a) modelo de grandes sinais, (b) modelo de
pequenos sinais.
Então, os sinais envolvidos no modelo médio das chaves em
MCD devem ser perturbados em torno de um ponto quiescente de
operação, como segue:
d ( t ) = D + dɵ ( t )
(12.23)
v1 ( t )
i1 ( t )
v2 ( t )
i2 ( t )
TS
TS
TS
TS
= V1 + v1 (t )
(12.24)
= I1 + iɵ1 (t )
(12.25)
= V2 + v2 (t )
(12.26)
= I 2 + i2 (t )
(12.27)
Onde, D é o valor quiescente da razão cíclica do transistor, V1 é
o valor quiescente da tensão média aplicada ao transistor, etc. As
variáveis v1 (t ) , dɵ ( t ) , etc., são pequenos sinais alternados (perturbações)
sobre seus respectivos valores quiescentes.
As equações (12.15) e (12.16) expressam as correntes médias nos
terminais i1 ( t ) T e i2 ( t ) T como função da razão cíclica do conversor
S
S
d ( t ) = d1 ( t ) e tensões médias nos terminais
v1 ( t )
TS
e
v2 ( t )
TS
.
Através da perturbação e linearização destas equações, encontraremos
Apostila de Controle de Conversores Estáticos
PPGEEL
160
Modelagem de conversores em condução descontínua
que xx e xxx são expressas como funções lineares de v1 (t ) , dɵ ( t ) e
v2 (t ) . Então, as equações das chaves para pequenos sinais podem ser
escritas da seguinte forma:
v
iɵ1 = 1 + j1 dɵ + g1 v2
r1
i2 = −
(12.28)
v2
+ j2 dɵ + g 2 v1
r2
(12.29)
Estas equações descrevem a entrada e saída do modelo de
pequenos sinais da Fig. 7.8. Os parâmetros r1, j1 e g1 podem ser
encontrados através da expansão de Taylor da equação (12.15). A
corrente média no transistor pode ser expressa da seguinte forma:
i1 ( t )
Ts
=
v1 ( t )
Ts
R e ( d1 )
(
= f1 v1 ( t )
Ts
, v2 ( t )
Ts
, d (t )
)
(12.30)
Vamos expandir esta expressão em uma série de Taylor
tridimensional sobre o ponto de operação quiescente (V1, V2, D):
∂f ( v , V , D )
I1 + ɵi1 ( t ) = f1 (V1 ,V2 , D ) + vɵ 1 ( t ) 1 1 2
∂v1
v =V
1
+ vɵ 2 ( t )
∂f1 (V1 , v2 , D )
∂v2
+ dɵ ( t )
1
∂f1 (V1 , V2 , d )
v2 = V2
∂d
(12.31)
d =D
+ termos de ordem sup erior não linear
Para simplificar a notação, os colchetes em ângulo denotando
valores médios são suprimidos na equação abaixo. Os termos constantes
em ambos os lados da equação (12.31) devem ser iguais:
I1 = f1 (V1 , V2 , D ) =
V1
Re ( D)
(12.32)
Usualmente, nós linearizamos as equações descartando os termos
não lineares de altas ordens. Os temos alternados de primeira ordem
remanescentes da equação (12.31) são equacionados:
ɵi1 ( t ) = vɵ 1 ( t ) 1 + vɵ 2 ( t ) g + dɵ ( t ) j
1
1
r1
(12.33)
Onde:
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
161
1 ∂f1 ( v1 ,V2 , D )
1
=
=
r1
R
∂v1
e ( D)
v =V
1
g1 =
j1 =
1
∂f1 (V1 , v2 , D )
∂v2
=0
(12.35)
v2 = V2
∂f1 (V1 , V2 , d )
∂d
(12.34)
=−
d =D
V1 ∂ R e ( d )
R ( D ) ∂d d = D
2
e
(12.36)
2V1
=
D Re ( D)
Embora, a resistência de entrada para pequenos sinais r1 é igual a
resistência efetiva Re, avaliado no ponto operacional quiescente. Este
termo descreve como variações em v1 ( t ) T afeta i1 ( t ) T via R e ( D ) .
S
S
O parâmetro g1 é igual a zero, desde que corrente média no transistor
i1 ( t ) T é dependente da tensão média no diodo v2 ( t ) T . O ganho de
S
S
pequenos sinais j1 descreve como variações na razão cíclica, a qual afeta
o valor de R e ( d ) , leva a variações em i1 ( t ) T .
S
De uma maneira similar, i2 ( t )
TS
da equação (12.16) pode ser
expressa por:
i2 ( t )
Ts
=
v1 ( t )
2
(
= f 2 v1 ( t )
Ts
R e ( d ( t ) ) v2 ( t )
Ts
, v2 ( t )
Ts
, d (t )
)
(12.37)
Ts
Vamos expandir esta expressão em uma série de Taylor
tridimensional sobre o ponto de operação quiescente (V1, V2, D):
∂f ( v ,V , D )
I 2 + ɵi 2 ( t ) = f 2 (V1 ,V2 , D ) + vɵ 1 ( t ) 2 1 2
∂v1
v =V
1
+ vɵ 2 ( t )
∂f 2 (V1 , v2 , D )
∂v2
+ dɵ ( t )
1
∂f 2 (V1 ,V2 , d )
v2 = V2
∂d
(12.38)
d =D
+ termos de ordem sup erior não linear
Pelo equacionamento dos termos constantes em ambos os lados
da equação (12.38), obtemos:
Apostila de Controle de Conversores Estáticos
PPGEEL
162
Modelagem de conversores em condução descontínua
V12
I 2 = f 2 (V1 , V2 , D ) =
R e ( D ) V2
(12.39)
Os termos de ordem superior podem ser descartados, levando aos
seguintes termos alternados lineares de primeira ordem:
ɵi 2 ( t ) = vɵ 2 ( t )  − 1

 r2
 ɵ
ɵ
 + v1 ( t ) g 2 + d ( t ) j2

(12.40)
Onde:
1 ∂f 2 (V1 , v2 , D )
=
r2
∂v2
v
2
g2 =
j2 =
v1 = V1
∂f 2 (V1 , V2 , d )
∂d
1
1
= 2
R M Re ( D)
(12.41)
=
2
M Re ( D)
(12.42)
= V2
∂f 2 ( v1 ,V2 , D )
∂v1
=
=−
d =D
∂ Re (d )
V12
2
Re ( D ) V2 ∂d d = D
(12.43)
2V1
=
DM R e ( D )
A resistência de saída r2 descreve como variações em v2 ( t )
influencia i2 ( t )
TS
TS
como ilustrado na Fig. 7.9, r2 é determinado pela
inclinação característica da fonte de potência, avaliado no ponte de
operação quiescente.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
163
Fig. 7.9 - Resistência de saída r2 é determinada pela inclinação
característica da fonte de potencia no ponte de operação quiescente.
Os valores dos parâmetros do modelo de pequenos sinais das chaves
para MCD da Fig. 7.8 são sumarizados na
Tabela 3.
Tabela 3 – Parâmetros do modelo de pequenos sinais das chaves em
MCD.
g1
0
j1
2V1
D Re
r1
Re
g2
2
M Re
j2
2V1
DM R e
r2
M 2 Re
A inclusão do modelo de pequenos sinais das chaves ao
conversor buck-boost resulta no circuito mostrado na Fig. 7.10.
Apostila de Controle de Conversores Estáticos
PPGEEL
164
Modelagem de conversores em condução descontínua
Fig. 7.10 - Modelo de pequenos sinais do conversor buck-boost obtido
pela inclusão do modelo de pequenos sinais das duas chave no circuito
original.
O modelo de circuito equivalente de pequenos sinais da Fig. 7.10
contém dois elementos dinâmicos: capacitor C e indutor L. A função de
controle da saída obtida pela solução do modelo de circuito equivalente
tem dois polos. Contudo, um polo devido ao capacitor C aparece em
baixas frequências enquanto o outro polo e o zero no semi plano direito
(SPD) devido ao indutor L, ocorre em frequências muito mais altas,
próximo da frequência de chaveamento do conversor. Portanto, na
prática, os conversores buck, boost e buck-boost essencialmente
evidencia uma função de transferência de um único polo, o qual é
influenciado insignificantemente pela dinâmica do indutor.
Uma aproximação simples para determinar a função de
transferência de baixa frequência para pequenos sinais do conversores
buck, boost e buck-boost é deixar a indutância L tender a zero ou seja é
um curto-circuito. A Fig. 7.11 mostra o circuito equivalente do
conversor buck-boost para pequenos sinais desprezando a indutância L.
Fig. 7.11 - Modelo de pequenos sinais para baixas frequências obtido
desprezando a indutância L.
A função de transferência de controle da saída para o conversor
buck-boost em MCD é encontrada deixando na Fig. 7.11.Solucionando,
chega-se a:
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
Gvd ( s ) =
vɵ
dɵ
=
vɵ g = 0
165
Gd 0
s
1+
wp
(12.44)
Gd 0 = j2 ( R \ \ r2 )
wp =
(12.45)
1
\
\
R
( r2 ) C
7.3
Simulação do Conversor Buck-Boost
Os parâmetros utilizados para a simulação e circuito simulado no
PSIM do conversor buck-boot em MCD são mostrados a seguir:
Tabela 4 – Parâmetros utilizados para a simulação.
Tensão de Entrada (Vg)
24 V
Frequência de chaveamento (f)
100 kHz
Tensão de saída (V)
-12 V
Capacitor (C)
1800 µF
Indutor (L)
2.2 µH
Razão cíclica (D)
0.26
Resistor de carga (R)
1.2 Ω
Frequência de corte do polo (wp)
2/RC
B0
V/D
B1
0
A0
1
A1
1/wp
Apostila de Controle de Conversores Estáticos
PPGEEL
166
Modelagem de conversores em condução descontínua
Fig. 7.12 - Circuito do conversor buck-boost simulado no PSIM.
A análise da resposta em frequência para o módulo e fase
simulado no PSIM é mostrado a seguir. Em vermelho é a resposta do
modelo obtido e em azul é a reposta do conversor buck-boost em MCD.
Apostila de Controle de Conversores Estáticos
PPGEEL
Modelagem de conversores em condução descontínua
amp(Vo 11)
167
amp(Vo12)
40
30
20
10
0
-10
phase(Vo11)
pha se(Vo12 )
180
160
140
120
100
80
60
10
100
1000
10000
Frequency (Hz)
Fig. 7.13 - Resposta em frequência de módulo e fase do modelo de
pequenos sinais (em vermelho) e do conversor buck-boost em MCD (em
azul).
Observa-se que para altas frequências há um pequeno erro no
modelo por causa da indutância (L) que foi desprezada.
A resposta da tensão na saída para um degrau de 10% na razão
cíclica é mostrado abaixo:
Vout
(-12.016/0.26)*Vref
-11.8
-12
-12.2
-12.4
-12.6
-12.8
-13
-13.2
-13.4
0.04
0.042
0.044
Time (s)
0.046
0.048
Fig. 7.14 - Reposta da tensão de saída para um degrau de 10% na razão
cíclica.
Notamos que para pequenas variações na razão cíclica o modelo
de pequenos sinais é válido. A figura abaixo mostra a resposta da tensão
de saída para um degrau de 90% na razão cíclica e como esperado o
modelo de pequenos sinais já não é mais válido.
Apostila de Controle de Conversores Estáticos
PPGEEL
168
Vout
Modelagem de conversores em condução descontínua
(-12.016/0.26)*Vref
-10
-20
-30
-40
0.04
0.042
0.044
0.046
0.048
T ime (s)
Fig. 7.15 - Resposta da tensão de saída para um degrau de 90% na
razão cíclica.
7.4
Conclusão
Com este trabalho foi possível obter o modelo de pequenos sinais
do conversor buck-boost operando em modo de condução descontínua e
validá-lo através de simulação observando tanto sua resposta em
frequência quanto a resposta a uma perturbação (degrau).
A simplificação feita desprezando a indutância para altas
frequências é válida conforme observamos na resposta em frequência.
Para grandes perturbações na razão cíclica o modelo de pequenos sinais
já não é mais válido mas não influência o controle pois para esta
situação são aplicadas proteções para o conversor.
Nota-se que a planta para condução descontínua é mais simples
que para condução contínua sendo que por este motivo alguns
conversores são propositalmente operados em condução descontínua
para facilitar o controle.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
8
8.1
169
Modelagem de conversor BUCK-BOOST
Controle de Conversores
Neste capítulo são apresentados o projetos e simulações de
controladores para os conversores Buck e Boost operando no modo de
condução contínua. Serão apresentados controladores individuais para as
plantas de corrente e tensão. Além disso serão avaliados o controle da
tensão de saída através do controle da corrente média e de pico do
indutor (controle modo corrente).
Antes da implementação dos controladores serão definidos alguns
critérios para o projeto no domínio da frequência, além da apresentação
da ferramenta computacional SISOTOOL, que simplifica a síntese dos
controladores através de uma interface gráfica amigável.
8.1.1
Critérios para o projeto de controladores de conversores
estáticos no domínio da frequência
No projeto de controle de conversores estáticos, ou de qualquer
tipo de controlador, devem ser observados alguns critérios para que
sejam garantidas a estabilidade e a resposta adequada do sistema em
malha fechada. No projeto no domínio da frequência de conversores
estáticos a definição da frequência de cruzamento por zero é limitada
teoricamente a um valor inferior à metade da frequência de comutação.
Em [20] é sugerida a limitação prática a um quarto da frequência de
comutação, além disso, a inclinação da curva de ganho nesta frequência
deve estar em -20 dB/Década.
A margem de fase do conversor deve estar entre 45º e 90º.
Margem de fase reduzida leva o sistema a apresentar elevado valor de
sobresinal, por outro lado uma margem muito elevada leva o sistema a
ter uma resposta transitória mais lenta.
Para que o conversor apresente um erro estático reduzido, deve-se
adicionar um pólo na origem (integrador), com isto o ganho de malha
aberta será muito grande em baixas frequências, o que elimina o erro
[20].
8.1.2
Introdução ao uso do SISOTOOL
O SISOTOOL é uma ferramenta gráfica para projeto de
compensadores para sistemas SISO (single-input/single-output)
disponível no MATLAB. Esta ferramenta permite o projeto utilizando
Apostila de Controle de Conversores Estáticos
PPGEEL
170
Controle de Conversores
ferramentas como o lugar das raízes, diagramas de Bode além das
técnicas de Nichols e Nyquist [21].
A ferramenta pode ser inicializado através do comando rltool(sys)
ou sisotool(sys). O parâmetro sys representa a função de transferência da
planta em análise. O exemplo abaixo apresenta os comandos necessários
para representar a planta de tensão do conversor Boost em condução
contínua:
L=4e-3; %Valor do indutor
C=1e-6; %Valor do capacitor
R=400; %Resistor de carga
Vg=200; %Tensão de entrada
D=0.25;
Exemplo de comandos utilizados para representar uma função de
transferência no MATLAB
Quando a ferramenta é carregada, esta apresenta duas janelas, a
“SISO Design for SISO Design Task” e a janela “Control and estimation
Tool Manager”. Na Fig. 8.1 é apresentada a janela “Control and
estimation Tool Manager”, nela estão os principais comandos de edição
do controlador, como a escolha da arquitetura, edição e avaliação do
desempenho deste.
Algumas das principais funções desta janela são:
Fig. 8.1 - Janela “Control and estimation Tool Manager”
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
171
Alteração de preferências de exibição: “Edit” “SISO Tools
preferences”. Na janela que se abrirá pode-se alterar o modo de exibição
das unidades de frequência, módulo e fase dos diagramas, além de
alterar o modo como são exibidas a função de transferência dos
compensadores.
Fig. 8.2 - Opções de unidade
SISOTOOLS
Fig. 8.3 - Aparência dos
compensadores
Seleção da arquitetura e dos dados da planta de controle:
Na aba “Architecture” a seleção de um entre as seis estruturas de
controle disponíveis é acessada pelo botão “Control Architecture.”. O
valor de cada um dos blocos pode ser selecionado através do botão
“System Data...”. ATENÇÃO: Quando a arquitetura é alterada os dados
do projeto atual são perdidos!
Fig. 8.4- Seleção da arquitetura de
controle
Fig. 8.5 - Edição dos dados da
planta
Edição do controlador: O posicionamento de pólos e zeros do
controlador, além do ajuste do ganho pode ser realizado através da aba
Apostila de Controle de Conversores Estáticos
PPGEEL
172
Controle de Conversores
“Compensator Editor”. O ajuste do compensador, como veremos, pode
ser realizado também de modo interativo com um dos diagramas
selecionados.
Fig. 8.6 - Edição do compensador.
Seleção dos diagramas de análise para ajuste gráfico: Na aba
“Graphical Tuning” podem ser selecionados até seis diagramas para
visualização simultânea, podendo ser realizada a análise em malha
fechada ou aberta. É comum a utilização do diagrama de Bode de malha
aberta para ajuste de compensadores utilizado em eletrônica de potência.
Após a seleção dos diagramas de análise, a janela “SISO Design for
SISO Design Task” é acessada através do botão “Show Design Plot”.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
173
Fig. 8.7 - Opções de ajuste gráfico.
Ajuste gráfico do controlador: Na janela “SISO Design for
SISO Design Task” o compensador pode ser ajustado através dos
seguintes comandos:
Ajuste de ganho: O ganho pode ser ajustado para selecionado o
botão “Ponteiro” que permite que o diagrama de módulo seja arrastado
para cima e para baixo.
Ajuste/Adição de pólos: zeros e pólos podem se adicionado com
a seleção dos botões “x” ou “o” e posterior clique na posição desejada
no gráfico. A posição pode ser modificada com a seleção da ferramenta
ponteiro, que permite que um pólo/zero seja arrastado para a posição
adequada no gráfico.
Para verificar a expressão do compensador editado seleciona-se
no menu “Disigns Edit Compensator”. Algumas análises do
desempenho do compensador podem ser obtidas através do menu
“Analysis”.
Na Fig. 8.8 é apresentada a situação da planta exemplo antes da
edição do controlador, neste editor, os pólos e zeros da planta são
representados respectivamente por ‘x’ e ‘o’ na cor azul. Na Fig. 8.9 é
apresentada a situação da planta após a edição do controlador, os
pólos/zeros do controlador são representados na cor vermelha.
Apostila de Controle de Conversores Estáticos
PPGEEL
174
Controle de Conversores
Fig. 8.8 - Ajuste gráfico do compensador – planta original.
Fig. 8.9 - situação da planta após a edição do compensador.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
8.1.3
8.1.3.1
175
Controle do Conversor Buck MCC
Definição da planta
Na Tabela 8.1 são apresentados os parâmetros do conversor Buck
utilizado para avaliação do controle. Com os parâmetros apresentados o
conversor opera no modo de condução contínua.
Tabela 8.1 - Parâmetros do conversor Buck
Tensão de entrada (Vi)
400 V
Tensão de saída (V)
48 V
Frequência de comutação (Fs)
20 kHz
Indutor (L)
500 uH
Capacitor (C)
100 uF
Resistor de carga (R)
2,304 Ω
O ganho do sensor de tensão utilizado é de 0,1 V/V, o ganho do
sensor de corrente é de 0,1 V/A e a tensão pico a pico da forma de onda
dente de serra utilizada no modulador é de 10 V.
8.1.3.2
Controle de tensão
O controle da tensão de saída pode ser executado com ação direta
sobre a razão cíclica do conversor, para isto será utilizada a estrutura de
controle apresentada na Fig. 8.10.
Vref
Controle
C(s)
Modulador
GPWM(s)
Planta
v(s)/d(s)
V
Sensor
Hv(s)
Fig. 8.10 – Malha de controle da tensão de saída do conversor Buck.
A função de transferência de laço aberto é apresentada na
equação (13.1), é a multiplicação dos blocos individuais da estrutura. O
Apostila de Controle de Conversores Estáticos
PPGEEL
176
Controle de Conversores
bloco C(s) representa o compensador a ser projetado, o bloco
Modulador representa o modulador por largura de pulso, cuja função de
transferência é apresentada na equação (13.2), com Vm representado a
tensão pico a pico da portadora.
A planta de tensão do conversor é apresentada na equação (13.3).
O sensor será representado apenas pelo ganho de tensão do componente.
FTMA1 ( s ) = C ( s ).GPWM ( S ).
GPWM ( s ) =
Vc( s )
.Hv( s )
d (s)
1
Vm




VC ( s )
1
= Vi 

L
d (s)
2
 LCs + s + 1 

R

(13.1)
(13.2)
(13.3)
Utilizando os parâmetros apresentados na Tabela 8.1 e o
compensador sendo considerado um ganho unitário é traçado o
diagrama de Bode da função de transferência de malha aberta,
apresentado na Fig. 8.11. Verifica-se que a planta possui dois pólos
localizados aproximadamente em 700 Hz.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
177
Open-Loop Bode Editor for Open Loop 1 (OL1)
0
-10
Magnitude (dB)
-20
-30
-40
Requirement:
-50
-60
G.M.: Inf
Freq: Inf
Stable loop
-70
-80
0
Phase (deg)
-45
-90
-135
P.M.: Inf
Freq: NaN
-180
1
10
2
10
3
10
Frequency (Hz)
4
10
10
5
Fig. 8.11 – Diagrama de Bode da FTMA da planta de controle de tensão
Buck sem compensação.
Esta planta será controlada por um controlador PID+pólo, com os
dois zeros localizados na mesma frequência dos pólos da planta, de
forma a anular sua influência. O pólo adicional será posicionado acima
da frequência de comutação, ajustado para interferir pouco na margem
de fase. A frequência de cruzamento por zero do ganho será de um
quarto da frequência de comutação.
A função de transferência de malha aberta considerando o
controlador projetado é apresentada na Fig. 8.12. A frequência de
cruzamento por zero é de 4,93 kHz e a margem de fase é de 74,5 graus.
Apostila de Controle de Conversores Estáticos
PPGEEL
178
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
80
60
Magnitude (dB)
40
20
Requirement:
0
-20
-40
G.M.: Inf
Freq: Inf
Stable loop
Phase (deg)
-45
-90
-135
P.M.: 74.2 deg
Freq: 4.93e+003 Hz
-180
1
2
10
10
3
4
10
10
Frequency (Hz)
10
5
Fig. 8.12 - Diagrama de Bode da FTMA da planta de controle de tensão
Buck com compensação.
O controlador C(s) é representado no domínio da frequência pela
equação (13.4), com os coeficientes apresentados na Tabela 8.2
C (s) = K
B2 s 2 + B1 s + B0
A2 s 2 + A1 s + A0
(13.4)
Tabela 8.2 – Coeficientes do controlador de tensão do conversor Buck.
Coeficiente
Valor
B2
1
B1
8944
B0
19998784
A2
1
A1
2,342e5
A0
0
K
738,287
Na Fig. 8.13 é apresentado o resultado de simulação de uma
elevação de 15% no valor da referência de tensão do controlador (15%
em relação ao valor nominal de 48 V). Observa-se um sobresinal de
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
179
cerca 5% nesta operação. A Fig. 8.14 apresenta o processo inverso, com
um degrau de -15% sendo aplicado. Neste caso o sobresinal é maior,
com cerca de 17%.
Referência
Tensão de Saída
Fig. 8.13 – Tensão de saída (em vermelho) e referência (azul) para
degrau de +15%.
Na Fig. 8.15 apresenta-se o resultado da tensão de saída para uma
referência composta de um sinal CC de 48 V e uma componente
senoidal de 7,2 V com frequência de 1 kHz. A tensão de saída segue
corretamente o sinal de referência, sem atraso ou variação de amplitude
perceptível.
Apostila de Controle de Conversores Estáticos
PPGEEL
180
Controle de Conversores
Tensão de Saída
Referência
Fig. 8.14 - Tensão de saída (em vermelho) e referência (azul) para
degrau de -15%.
Fig. 8.15 – Tensão de saída (vermelho) e referência senoidal de 1 kHz
(azul).
8.1.3.3
Controle de corrente
A corrente no indutor no conversor Buck pode ser controlada
através da variação da razão cíclica imposta a chave. A estrutura
utilizada para realizar o controle de corrente é apresentada na Fig. 8.16.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
181
Fig. 8.16 - Malha de controle da corrente do indutor do conversor
Buck.
A planta de corrente do conversor Buck operando no modo de
condução contínua é apresentada na equação (13.5). Para obtenção da
função de transferência de malha aberta, utiliza-se o mesmo
procedimento apresentado na seção 8.1.3.2, neste caso o sensor é
representado pelo ganho do sensor de corrente utilizado.


I L ( s ) Vi 
RCs + 1 
= 

d ( s ) R  LCs 2 + L s + 1 


R


(13.5)
O diagrama de Bode da função de transferência de malha aberta
é apresentado na Fig. 8.17. Com os parâmetros utilizados neste projeto
ocorre o cancelamento de um dos pólos da planta pelo zero da planta.
Este efeito faz com que a planta de segunda ordem tenha um
comportamento similar a uma planta de primeira ordem, principalmente
em relação à fase que varia de zero a -90 graus.
Apostila de Controle de Conversores Estáticos
PPGEEL
182
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
10
5
Magnitude (dB)
0
-5
-10
-15
G.M.: Inf
Freq: NaN
Stable loop
-20
-25
45
Phase (deg)
0
-45
-90
-135
P.M.: 95.5 deg
Freq: 9.69e+003 rad/sec
-180
2
10
3
4
10
10
5
10
Frequency (rad/sec)
Fig. 8.17 - Diagrama de Bode da FTMA da planta de controle de
corrente do conversor Buck sem compensação.
O controlador utilizado será um PI+pólo. O integrador na origem
proporciona um elevado ganho nas baixas frequência eliminando o erro
estacionário. Com o zero do controlador será anulado o efeito do
segundo pólo da planta, com isto a inclinação de ganho da FTMA na
região de cruzamento por zero é de -20 dB/década. O pólo adicional é
posicionado acima da frequência de comutação do conversor, a fim de
atenuar ruídos da malha de realimentação. A frequência de cruzamento
por zero do ganho é de cerca de um quarto da frequência de comutação.
A FTMA compensada é apresentada na Fig. 8.18, observa-se que
o frequência de cruzamento obtida é de 4,99 kHz com margem de fase
de 75 graus. Estes valores estão de acordo com os critérios de
estabilidade e desempenho considerados.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
183
Open-Loop Bode Editor for Open Loop 1 (OL1)
60
40
Magnitude (dB)
20
0
-20
-40
G.M.: Inf
Freq: Inf
Stable loop
-60
Phase (deg)
-80
-45
-90
-135
P.M.: 75 deg
Freq: 4.99e+003 Hz
-180
1
10
2
10
3
4
10
10
5
10
6
10
Frequency (Hz)
Fig. 8.18 - Diagrama de Bode da FTMA da planta de controle de
corrente do conversor Buck com compensação.
O controlador C(s) é representado no domínio da frequência pela
equação (13.4), com os coeficientes apresentados na
Tabela 8.3
Tabela 8.3 – Coeficientes do controlador de corrente do conversor
Buck.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
4472
1
2,525e5
0
966460
Apostila de Controle de Conversores Estáticos
PPGEEL
184
Controle de Conversores
O resultado do degrau na referência de corrente para variação
positiva de 15% é mostrado na Fig. 8.19 e para variação negativa na Fig.
8.20. As variações aplicadas correspondem a 15% do valor da corrente
nominal no indutor. O sobresinal obtido na variação positiva é de 2,3%
e na variação negativa é de 13%.
Referência
Corrente no indutor
Fig. 8.19 – Corrente no indutor (vermelho) e referência (azul) para
degrau de +15%.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
185
Corrente no indutor
Referência
Fig. 8.20 - Corrente no indutor (vermelho) e referência (azul) para
degrau de -15%.
O resultado da corrente no indutor para uma referencia de
corrente composta por um sinal contínuo de 20 A adicionado a uma
senóide com amplitude de 3 A (15%) é apresentado na Fig. 8.21. Nesta
situação não se identifica erro da amplitude ou atraso de fase no sinal de
corrente gerado em relação à referência.
Apostila de Controle de Conversores Estáticos
PPGEEL
186
Controle de Conversores
Fig. 8.21 - Corrente no indutor (vermelho) e referência senoidal de 1
kHz (azul).
8.1.3.4
Controle em cascata de tensão e corrente
Nesta metodologia a tensão de saída é controlada através de uma
malha externa que fornece uma referencia de corrente para a malha
interna de controle de corrente conforme apresentado na Fig. 8.22. Nesta
abordagem a malha de controle interna é mais rápida que a malha de
controle externa, em termos prática, no mínimo cinco vezes mais rápida.
A malha de controle de corrente já foi projetada no item 8.1.3.3,
sendo utilizado o mesmo projeto do controlador nesta seção. A função
de transferência de malha aberta para o controle de tensão é apresentada
na equação (13.6).
Fig. 8.22 - Malha de controle de corrente e tensão do conversor Buck.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
FTMAV ( s ) = C 2( s ).FTMFi .
187
Vc( s )
.Hv( s )
I L (s)
(13.6)
A planta da tensão do capacitor em relação a corrente no indutor
já foi obtida neste trabalho, sendo reapresentada na equação (13.7). A
função de transferência de malha fechada da planta de corrente pode ser
obtida a partir da equação (13.8).
VC ( s )
 1 
= R

I L (s)
 RCs + 1 
(13.7)
I L (s)
d (s)
FTMFi ( s ) =
I L (s)
1 + C1( s ).GPWM ( S ).
.Hi ( s )
d (s)
(13.8)
C1( s ).GPWM ( S ).
Devido a presença do integrador na planta de controle de
corrente, ao multiplicarmos por S o numerador e o denominador, o
termo S é simplificado, aparecendo apenas multiplicando o 1 do
denominador. Como a frequência da malha externa é muito mais lenta
que a malha interna, faz-se S 0 , deste modo a expressão para a FTMFi
da corrente é simplificada, de acordo com a equação (13.9):
FTMFi ( s ) ≈
1
Hi ( s )
(13.9)
Na Fig. 8.23 é apresentado o diagrama de Bode da FTMAv
considerando a simplificação na planta de corrente, este resultado pode
ser comparado com a Fig. 8.24 que apresenta o diagrama de Bode da
FTMA considerando a função de malha fechada completa de corrente. O
ganho CC das duas plantas é idêntico, na frequência de 1kHz (1/5 da
Fcz da planta e corrente) a diferença de fase é inferior a 15 graus. Deste
modo considera-se a aproximação válida para frequências de interesse.
Apostila de Controle de Conversores Estáticos
PPGEEL
188
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
10
5
Magnitude (dB)
0
-5
-10
-15
-20
G.M.: Inf
Freq: NaN
Stable loop
-25
-30
0
Phase (deg)
-45
-90
-135
P.M.: 116 deg
Freq: 1.43e+003 Hz
-180
1
10
2
10
3
10
Frequency (Hz)
4
10
5
10
Fig. 8.23 – Diagrama de Bode da FTMA da planta de controle de tensão
do conversor Buck sem compensação considerando FTMFi
simplificada.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
189
Open-Loop Bode Editor for Open Loop 1 (OL1)
20
0
Magnitude (dB)
-20
-40
-60
-80
-100
G.M.: 27.9 dB
Freq: 1.4e+004 Hz
Stable loop
-120
-140
0
Phase (deg)
-45
-90
-135
-180
-225
P.M.: 100 deg
Freq: 1.55e+003 Hz
-270
1
10
2
10
10
3
4
10
5
10
6
10
Frequency (Hz)
Fig. 8.24 – Diagrama de Bode da FTMA da planta de controle de tensão
do conversor Buck sem compensação considerando FTMFi completa.
Para o controle será ajustado um controlador PI+pólo, com o zero
ajustado no pólo da planta de tensão. O segundo pólo será adicionado
acima da frequência de cruzamento por zero a fim de minimizar ruídos
na malha de controle. A Fig. 8.25 apresenta a FTMAv compensada.
Apostila de Controle de Conversores Estáticos
PPGEEL
190
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
20
Magnitude (dB)
0
-20
-40
-60
G.M.: Inf
Freq: Inf
Stable loop
-80
Phase (deg)
-100
-90
-135
P.M.: 84.7 deg
Freq: 996 Hz
-180
2
10
3
10
4
10
Frequency (Hz)
5
10
6
10
Fig. 8.25 – Diagrama de Bode da FTMA da planta de controle de tensão
do conversor Buck com compensação.
O controlador de tensão do controle em cascata (C2(s)) é
representado no domínio da frequência pela equação (13.4), com os
coeficientes apresentados na Tabela 8.4. O controlador de corrente é o
mesmo projetado no item 8.1.3.3.
Tabela 8.4 – Coeficientes do controlador de tensão do controle em
cascata do conversor Buck.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
4355
1
6,83e4
0
42921
O resultado do degrau na referência de tensão para variação
positiva de 15% é mostrado na Fig. 8.26 e para variação negativa na Fig.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
191
8.27. É observado sobre sinal na forma de onda de tensão e corrente no
indutor. O tempo de estabilização é inferior a 1 ms.
Fig. 8.26 – Quadro superior: Tensão de saída (vermelho) e referência
(azul)
Quadro inferior: Corrente no indutor (vermelho) para degrau de
+15%.
Na Fig. 8.28 apresenta-se o resultado para uma referência
composta de um sinal CC de 48 V e uma componente senoidal de 7,2 V
com frequência de 1 kHz. A tensão de saída já apresenta atraso de fase
considerável, mas mantém a amplitude.
Apostila de Controle de Conversores Estáticos
PPGEEL
192
Controle de Conversores
Tensão de Saída
Referência
Fig. 8.27 – Quadro superior: Tensão de saída (vermelho) e referência
(azul)
Quadro inferior: Corrente no indutor (vermelho) para degrau de 15%.
Fig. 8.28 – Tensão de saída (vermelho) e referência senoidal de 1 kHz
(azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
193
Fig. 8.29 é apresentado o resultado da tensão de saída no
momento de uma rejeição de carga de 50%. A tensão sobe
momentaneamente para 56 V (aumento de quase 20%) sendo
rapidamente reduzida para o valor nominal. Observa-se que a tensão no
modulador satura no valor inferior, isto significa que o conversor não
pode reduzir a corrente com o ritmo solicitado pelo controlador.
Na Fig. 8.30 é apresentada a tensão de saída no momento que o
conversor tem a potência de saída aumentada de 50 para 100% da carga
nominal, neste caso a tensão de saída sobre uma redução de quase 20%
sendo recuperada rapidamente pelo controle para o valor nominal.
A banda do controlador de tensão poderia ser aumentada, o que
reduziria a perturbação no caso do degrau de carga de 50% para 100%,
já que o controle de corrente não chega a saturar nesta situação. No
entanto há também o compromisso de manter uma relação deste
controlador em relação ao controle de corrente, caso o controle de
corrente não responda corretamente a referência de tensão o sistema
pode oscilar.
Apostila de Controle de Conversores Estáticos
PPGEEL
194
Controle de Conversores
Tensão de Saída
Referência
Ref. Corrente
Tensão no modulador
Fig. 8.29 – quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente de referência (verde) e Tensão na
entrada do modulador (Roxo) para redução de 50% da carga.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
195
Referência
Tensão de Saída
Tensão no modulador
Ref. Corrente
Fig. 8.30 – Tensão de saída (vermelho) e referência (azul) para
incremento de 50% da carga.
8.1.3.5
Controle em Modo de Corrente
Neste método de controle a tensão de saída é controlada através
do valor de pico da corrente no indutor. O diagrama de controle é
apresentado na Fig. 8.31. O bloco comparador da corrente será
representado apenas pelo ganho de corrente obtido, dado pelo inverso do
ganho do sensor de corrente.
Fig. 8.31 – Malha de controle do converso Buck em modo corrente.
O modelo para a planta de tensão em relação a corrente do
indutor foi apresentado na equação (13.7). O ganho do sensor de
Apostila de Controle de Conversores Estáticos
PPGEEL
196
Controle de Conversores
corrente desta planta será alterado para 0,05 V/A visando limitar a queda
de tensão em 1 V na operação nominal. O diagrama de Bode da FTMA
desta planta de controle é apresentado na Fig. 8.32.
Open-Loop Bode Editor for Open Loop 1 (OL1)
10
5
Magnitude (dB)
0
-5
-10
-15
-20
G.M.: Inf
Freq: NaN
Stable loop
-25
-30
0
Phase (deg)
-45
-90
-135
P.M.: 116 deg
Freq: 1.43e+003 Hz
-180
10
1
2
10
3
10
Frequency (Hz)
10
4
10
5
Fig. 8.32 - Diagrama de Bode da FTMA da planta de controle em modo
corrente do conversor Buck sem compensação.
O diagrama de Bode da planta de controle com o controlador
PI+pólo ajustado é apresentado na Fig. 8.33. A margem de fase é de 82
graus com a frequência de cruzamento por zero do ganho em 4,68 kHz.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
197
Open-Loop Bode Editor for Open Loop 1 (OL1)
40
Magnitude (dB)
20
0
-20
-40
G.M.: Inf
Freq: Inf
Stable loop
-60
Phase (deg)
-80
-90
-135
P.M.: 83.3 deg
Freq: 4.68e+003 Hz
-180
2
10
3
10
4
10
Frequency (Hz)
5
10
10
6
Fig. 8.33 - Diagrama de Bode da FTMA da planta de controle em modo
corrente do conversor Buck com compensação.
O controlador de tensão do controle em modo corrente é
representado no domínio da frequência pela equação (13.4), com os
coeficientes apresentados na
Tabela 8.5. O circuito utilizado na simulação do controle do
PSIM é apresentado na Fig. 8.34.
Tabela 8.5 – Coeficientes do controlador de tensão do controle em
modo corrente do conversor Buck.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
4274
1
2,455e5
0
3,63e5
Apostila de Controle de Conversores Estáticos
PPGEEL
198
Controle de Conversores
Fig. 8.34 - Circuito simulado no PSIM para avaliação do controle em
modo corrente do conversor Buck
Na Fig. 8.35 é apresentado o resultado da tensão de saída para
uma variação de 15% na referência, a situação oposta é apresentada na
Fig. 8.36 onde a referência é aumentada em 15% em relação ao valor
nominal. Nas duas figuras são apresentadas também a tensão da saída do
controlador e a corrente medida no sensor.
Tensão de Saída
Referência
Limite de corrente
Corrente no sensor
Fig. 8.35 - Quadro superior: Tensão de saída (vermelho) e referência
(azul)
Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para degrau de +15%.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
199
Referência
Tensão de Saída
Limite de corrente
Corrente no sensor
Fig. 8.36 - Quadro superior: Tensão de saída (vermelho) e referência
(azul)
Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para degrau de (-15%).
Na Fig. 8.37 apresenta-se o resultado para uma referência
composta de um sinal CC de 48 V e uma componente senoidal de 7,2 V
com frequência de 1 kHz. A tensão de saída apresenta um pequeno
atraso em relação a referência, no entanto a amplitude é mantida.
Na Fig. 8.38 é apresentado o comportamento da tensão de saída e
da corrente de entrada (Isens) para uma redução de 50% na carga. O
controlador satura no valor limitante inferior, o que provoca um
oscilação durante o transitório, que dura menos que 1 ms.
Apostila de Controle de Conversores Estáticos
PPGEEL
200
Controle de Conversores
Fig. 8.37 – Tensão de saída (vermelho) e referência senoidal de 1 kHz
(azul).
Tensão de Saída
Referência
Limite de corrente
Corrente no sensor
Fig. 8.38 – Quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para redução de 50% da carga.
Na Fig. 8.39 é apresentado o comportamento da saída para um
aumento de carga de 50% para 100% da carga nominal. Nesta situação
verifica-se o comportamento adequado da tensão, sendo estabilizada em
menos de 1 ms pelo controlador.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
201
Referência
Tensão de Saída
Limite de corrente
Corrente no sensor
Fig. 8.39 – Quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para aumento de 50% da carga.
8.1.4
8.1.4.1
Controle do Conversor Boost CCM
Definição da planta
Na Tabela 8.6 são apresentados os parâmetros do conversor
Boost utilizado para análise do controle. Com os parâmetros
apresentados o conversor opera no modo de condução contínua.
Tabela 8.6 - Parâmetros do conversor Boost
Tensão de entrada
200 V
Tensão de saída
400 V
Frequência de comutação
70 kHz
Indutor
5 mH
Capacitor
100 uF
Resistor de carga
2,304 Ω
Apostila de Controle de Conversores Estáticos
PPGEEL
202
Controle de Conversores
O ganho do sensor de tensão utilizado é de 0,01 V/V, o ganho do
sensor de corrente é de 0,1 V/A e a tensão pico a pico da tensão dente de
serra utilizada no modulador é de 10 V.
8.1.4.2
Controle de Tensão
O controle da tensão de saída do conversor Boost pode ser
executado com ação direta sobre a razão cíclica imposta a chave do
conversor, para isto será utilizada a estrutura de controle apresentada na
Fig. 8.40.
Vref
Controle
C(s)
Modulador
GPWM(s)
Planta
v(s)/d(s)
V
Sensor
Hv(s)
Fig. 8.40 - Malha de controle de tensão do conversor Boost
O modelo da planta de tensão do conversor já foi obtido neste
trabalho, sendo reapresentado na equação (13.10). Esta planta possui um
zero no semi-plano direito do plano S. Este zero acaba se comportando
com um pólo em relação à resposta fase do sistema.
−VL
s + VR[1 − D ]
Vc ( s )
1
−D
=
d ( s ) RLCs 2 + Ls + R[1 − D ]2
(13.10)
A função de transferência de malha aberta é obtida através da
multiplicação dos elementos da malha, conforme equação (13.11).
Considerando os parâmetros apresentados na
Tabela 8.6 e o controlador como um ganho unitário é traçado o
diagrama de bode da FTMAbv apresentado na Fig. 8.41.
FTMAbv ( s ) = C ( s ).GPWM ( S ).
V (s)
.Hv( s )
d (s)
Apostila de Controle de Conversores Estáticos
(13.11)
PPGEEL
Controle de Conversores
203
Open-Loop Bode Editor for Open Loop 1 (OL1)
50
Magnitude (dB)
40
30
20
10
G.M.: -38.1 dB
Freq: 1.78e+003 Hz
Unstable loop
0
Phase (deg)
-10
360
270
180
P.M.: -82.2 deg
Freq: 3.21e+004 Hz
90
10
2
3
4
10
10
10
5
Frequency (Hz)
Fig. 8.41 – Diagrama de bode da FTMA do controle de tensão do
conversor Boost sem compensação.
Na frequência de cruzamento por zero desejada (17,5 kHz) a
margem de fase já está próxima de zero. Se considerarmos aplicação de
um controlador PID, com os zeros anulando o efeito dos dois pólos da
planta, e ganho ajustado para que a frequência de cruzamento por zero
seja de 17,5 kHz o sistema será instável. Para evitar a utilização de um
controlador com mais sofisticado a especificação de frequência de
cruzamento por zero será reduzida. Na Fig. 8.42 é apresentado o ajuste
do controlador considerando a frequência de cruzamento por zero em
100 Hz. Este valor teve que ser fortemente reduzido já que a planta não
apresenta inclinação de -20 dB/Década na região de ressonância dos
pólos complexos conjugados.
Apostila de Controle de Conversores Estáticos
PPGEEL
204
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
20
10
Magnitude (dB)
0
-10
-20
-30
-40
G.M.: 30.1 dB
Freq: 7.74e+003 Hz
Stable loop
-50
-60
315
Phase (deg)
270
225
180
135
P.M.: 96.5 deg
Freq: 104 Hz
90
1
10
2
10
3
4
10
10
10
5
6
10
Frequency (Hz)
Fig. 8.42 - Diagrama de bode da FTMA do controle de tensão do
conversor Boost compensada.
O controlador C(s) é representado no domínio da frequência pela
equação (13.4), com os coeficientes apresentados na Tabela 8.7.
Tabela 8.7 – Coeficientes do controlador de tensão do conversor Boost.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
1
15344
58859584
1
2,256e5
0
3,0464
Na Fig. 8.43 é apresentado o comportamento da tensão de saída
frente a uma variação de 15% na referência de tensão. Observa-se a
ausência de sobresinal e erro estático, no entanto observa-se um
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
205
comportamento oscilatório da tensão durante o período de estabilização.
Na Fig. 8.44 é apresentado o resultado de uma variação de -15% na
referência. Neste caso também é verificado um comportamento
oscilatório da tensão de saída durante a estabilização da tensão.
Referência
Tensão de Saída
Fig. 8.43 – Tensão de saída (em vermelho) e referência (azul) para
degrau de +15%.
Na Fig. 8.45 é apresentado o comportamento da tensão de saída
quando a referência é composta por um valor CC de 400 V adicionado a
uma senóide de amplitude 60 V com frequência de 100 Hz. Observa-se
que há um atraso de 40 graus em relação à referência, além de uma
atenuação considerável.
Apostila de Controle de Conversores Estáticos
PPGEEL
206
Controle de Conversores
Tensão de Saída
Referência
Fig. 8.44 – Tensão de saída (em vermelho) e referência (azul) para
degrau de -15%.
Fig. 8.45 – Tensão de saída (vermelho) e referência senoidal de 100 Hz
(azul)
8.1.4.3
Controle de Corrente
No conversor Boost a corrente do indutor pode ser controlada
através do ajuste adequado da razão cíclica. Na Fig. 8.46 é apresentada a
estrutura de controle que será utilizada para este fim.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
207
Fig. 8.46 – Malha de controle de corrente do conversor Boost.
A planta da corrente do indutor em relação a razão cíclica já foi
levantada neste documento, sendo repetida na equação (13.12). Esta
planta apresenta dois pólos e um zero.
I L (s)
VRCs + 2V
=
d ( s ) RLCs 2 + Ls + R[1 − D ]2
(13.12)
Escrevendo-se a função de transferência de malha aberta,
conforme procedimento apresentado no item 8.1.3.2, e considerando o
controlador como um ganho unitário pode ser obtido o diagrama de
Bode, apresentado na Fig. 8.47.
Open-Loop Bode Editor f or Open Loop 1 (OL1)
-5
-10
Magnitude (dB)
-15
-20
-25
-30
G.M.: Inf
Freq: NaN
Stable loop
-35
-40
45
Phase (deg)
0
-45
-90
P.M.: Inf
Freq: NaN
-135
2
10
3
4
10
10
5
10
Frequency (rad/sec)
Fig. 8.47 - Diagrama de Bode da FTMA do controle de corrente do
conversor Boost sem compensação.
Apostila de Controle de Conversores Estáticos
PPGEEL
208
Controle de Conversores
Observa-se que o zero e os pólos estão próximos, mesmo não
ocorrendo um cancelamento, o sistema apresenta a resposta de fase
similar a um sistema de primeira ordem. Como controlador será ajustado
um PI+pólo, o zero deste controlador será posicionado na mesma
frequência real dos pólos complexos conjugados e o pólo adicional,
inserido para evitar ruído de alta frequência na malha de controle, é
posicionado acima da frequência de comutação.
O diagrama de Bode a FTMA compensada é apresentado na Fig.
8.48. A margem de fase é de 75,2 graus e a frequência de cruzamento
por zero obtida é de 16,1 kHz.
Open-Loop Bode Editor for Open Loop 1 (OL1)
40
Magnitude (dB)
30
20
10
0
G.M.: Inf
Freq: Inf
Stable loop
Phase (deg)
-45
-90
-135
P.M.: 75.2 deg
Freq: 1.61e+004 Hz
2
10
3
10
Frequency (Hz)
4
10
5
10
Fig. 8.48 - Diagrama de Bode da FTMA do controle de corrente do
conversor Boost com compensação.
O controlador C(s) é representado no domínio da frequência pela
equação (13.4), com os coeficientes apresentados na Tabela 8.8.
Tabela 8.8 – Coeficientes do controlador de corrente do conversor
Boost.
Coeficiente
B2
B1
Valor
0
1
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
209
B0
A2
A1
A0
K
7865
1
6,453e5
0
6,55e7
Na Fig. 8.49 é apresentado o comportamento da corrente no
indutor frente a um degrau na referência de corrente de 15% em relação
ao valor nominal. Observa-se a rápida ação do controlador além de um
pequeno sobre sinal. Na Fig. 8.50 é apresentado o resultado na tensão de
saída para uma redução de 15% na referência de corrente.
Referência
Corrente no indutor
Fig. 8.49 – Corrente no indutor (vermelho) e referência (azul) para
degrau de +15%.
Apostila de Controle de Conversores Estáticos
PPGEEL
210
Controle de Conversores
Referência
Corrente no indutor
Fig. 8.50 - Corrente no indutor (vermelho) e referência (azul) para
degrau de -15%.
Na Fig. 8.51 é apresentada a corrente no indutor para uma
referência composta por um valor contínuo de 2 A e uma senóide com
amplitude de 0,3 A com frequência de 1 kHz. Verifica-se que a corrente
obtida segue corretamente a referência, exceto pela ondulação de alta
frequência inerente ao chaveamento do conversor.
Fig. 8.51 – Corrente no indutor (vermelho) e referência senoidal de 1
kHz (azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
8.1.4.4
211
Controle de Corrente e Tensão – Controle em cascata
A tensão de saída pode ser controlada através do valor médio de
corrente no indutor do conversor Boost. Neste caso é necessário o
emprego de dois controladores, internamente é utilizado um controlador
de corrente do indutor. A referência de corrente deste controlador é
obtida do segundo controlador, que controla o valor da tensa ode saída.
Fig. 8.52 é apresentado o diagrama de controle que será utilizado.
Fig. 8.52 – Diagrama de controle de corrente e tensão do conversor
Boost MCC
Em [22] é apresentada um modelo simplificado para a planta de
corrente em relação à razão cíclica do conversor Boost MCC, própria
para o uso em sistemas em cascata. Esta planta é apresentada na equação
(13.13).
I L (s) V
=
d ( s ) Ls
(13.13)
A planta de tensão leva em conta o valor médio da razão cíclica e
possui dinâmica de primeira ordem, dependendo da carga e do capacitor
de saída. Esta planta é apresentada na equação (13.14).
V ( s)
RD
=
I L ( s ) RCs + 1
(13.14)
Inicialmente será projetado o controlador da malha interna. Na
Fig. 8.53 é apresentado o diagrama de Bode da FTMA da planta de
corrente simplificada. Observa-se uma inclinação de -20 dB/Década
devido ao único pólo na origem. A ajuste de um controlador PI+pólo
torna possível a obtenção da margem de fase e a frequência de
cruzamento por zero especificados.
Na Fig. 8.54 é apresentado o diagrama de Bode da FTMA da
planta com a compensação. Neste caso foi obtida uma margem de fase
de 72,5 graus e a frequência de cruzamento por zero é de 16,3 kHz.
Apostila de Controle de Conversores Estáticos
PPGEEL
212
Controle de Conversores
Open-Loop Bode Editor f or Open Loop 1 (OL1)
50
40
Magnitude (dB)
30
20
10
0
G.M.: Inf
Freq: NaN
Stable loop
-10
Phase (deg)
-20
-90
-135
P.M.: 90 deg
Freq: 159 Hz
-180
0
1
10
2
10
10
Frequency (Hz)
10
3
10
4
Fig. 8.53 – Diagrama de Bode da FTMA da planta de corrente
simplificada do conversor Boost.
Open-Loop Bode Editor f or Open Loop 1 (OL1)
100
Magnitude (dB)
50
0
-50
G.M.: -Inf dB
Freq: 0 Hz
Stable loop
-100
-90
Phase (deg)
P.M.: 75.2 deg
Freq: 1.63e+004 Hz
-120
-150
-180
2
10
3
10
10
4
5
10
6
10
7
10
Frequency (Hz)
Fig. 8.54 - Diagrama de Bode da FTMA da planta de corrente
simplificada do conversor Boost com compensação.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
213
O controlador de corrente C1(s) é representado no domínio da
frequência pela equação (13.4), com os coeficientes apresentados
naTabela 8.9.
Tabela 8.9 – Coeficientes do controlador de corrente para o controle em
cascata do conversor Boost.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
1,896e4
1
1,348e6
0
1,365e8
Para o projeto do controlador de tensão é necessário que seja
obtida a representação da FTMA de tensão. A malha interna de corrente
é representada pelo seu valor em malha fechada. Utilizando o mesmo
procedimento descrito no item 8.1.3.4, a função de transferência de
malha fechada da malha de corrente será representada pela equação
(13.15). A função de transferência de malha aberta para a malha de
tensão é descrita na equação (13.16).
FTMFi ( s ) ≈
1
Hi ( s )
FTMAV ( s ) = C ( s ).FTMFi .
(13.15)
V (s)
.Hv( s )
I L (s)
(13.16)
O diagrama de Bode da FTMA de tensão é apresentado na Fig.
8.55. Observa-se o comportamento característico de sistemas de
primeira ordem, com fase inicial nula e fase final de 90 graus.
Apostila de Controle de Conversores Estáticos
PPGEEL
214
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
30
25
Magnitude (dB)
20
15
10
5
G.M.: Inf
Freq: NaN
Stable loop
0
-5
0
Phase (deg)
-45
-90
-135
P.M.: 92.9 deg
Freq: 7.95e+003 Hz
-180
1
10
2
3
10
10
4
10
Frequency (Hz)
Fig. 8.55 – Diagrama de Bode da FTMA da planta de tensão do
conversor Boost para o controle em cascata.
Esta planta pode ser controlada com o ajuste adequado de um
controlador PI+pólo. O zero do controlador será posicionado na mesma
frequência do pólo da planta de tensão. O pólo adicional é posicionado
acima da frequência de cruzamento por zero. Na Fig. 8.56 é apresentado
o diagrama de Bode da FTMA após o ajuste do controlador. Este
controlador (C2(s)) é representado no domínio da frequência pela
equação (13.4), com os coeficientes apresentados na Tabela 8.8.
Tabela 8.10 – Coeficientes do controlador de tensão do controle em
cascata do conversor Boost.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
2509
1
6,343e4
0
7905
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
215
Open-Loop Bode Editor for Open Loop 1 (OL1)
20
Magnitude (dB)
0
-20
-40
-60
G.M.: Inf
Freq: Inf
Stable loop
-80
Phase (deg)
-100
-90
-135
P.M.: 84.4 deg
Freq: 987 Hz
-180
10
2
10
3
4
10
Frequency (Hz)
5
10
10
6
Fig. 8.56 – Diagrama de Bode da FTMA da planta de tensão
compensada do conversor Boost para o controle em cascata.
Na Fig. 8.57 é apresentado o comportamento da tensão de saída
em resposta a um degrau na referência de tensão de 15% em relação ao
valor nominal. Na Fig. 8.58 é apresentado o resultado na tensão de saída
para uma redução de 15% na referência de corrente. Observa-se que o
comportamento inicial da saída é inverso em relação a referência. Este
fato é resultado da presença de um zero no semi-plano direito do plano S
na planta do conversor. Fisicamente sabe-se que para aumentar a tensão
de saída do conversor é necessário aumentar a corrente no indutor, no
entanto para aumentar a corrente é necessário manter a chave mais
tempo fechada, como a energia é transferida para a saída somente
quando a chave está aberta, nos primeiros instantes do transitório menos
energia é transferida para a carga o que provoca a queda da tensão de
saída, depois que a corrente sobe a tensão volta a crescer.
Apostila de Controle de Conversores Estáticos
PPGEEL
216
Controle de Conversores
Referência
Tensão de Saída
Fig. 8.57 – Tensão de saída (vermelho) e referência (azul) para degrau
de +15%.
Tensão de Saída
Referência
.
Fig. 8.58 – Tensão de saída (vermelho) e referência (azul) para degrau
de -15%.
Na Fig. 8.59 é apresentado o comportamento da tensão de saída e
da corrente no indutor para remoção e inserção de 50% da carga
nominal. Inicialmente o converso opera com 100% da capacidade, em
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
217
23 ms 50% da carga é removida. A tensão sobre uma rápida elevação de
11%, que é prontamente corrigida pelo controle através da redução da
corrente no indutor. Em 33 ms o conversor volta a carga nominal, neste
instante ocorre uma redução na tensão de saída que é recuperada em
cerca de 2ms pelo controle.
Tensão de Saída
Referência
Corrente no indutor
Fig. 8.59 Quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente no indutor para degrau de +/- 50% da
carga.
Na Fig. 8.60 é apresentado o comportamento da tensão de saída
quando a referência de tensão é composta por um valor contínuo de 400
V adicionado a uma senóide de amplitude 60 V com frequência de 500
Hz. Observa-se que há um atraso de fase em relação à referência, além
de uma atenuação de 33%.
Apostila de Controle de Conversores Estáticos
PPGEEL
218
Controle de Conversores
Fig. 8.60 – Tensão de saída (vermelho) e referência senoidal de 500 Hz
(azul).
8.1.4.5
Controle em Modo de Corrente
Neste método de controle a tensão de saída é controlada através
do valor de pico da corrente no indutor do Boost. O sensor de corrente é
posicionado em série com a chave. O diagrama de controle é
apresentado na Fig. 8.61. O bloco comparador da corrente será
representado apenas pelo ganho de corrente obtido, dado pelo inverso do
ganho do sensor de corrente.
Fig. 8.61 – Malha de controle do converso Boost em modo corrente.
O modelo para a planta de tensão em relação a corrente do
indutor foi apresentado na equação (13.14). O diagrama de Bode da
FTMA desta planta de controle é apresentado na Fig. 8.62.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
219
Open-Loop Bode Editor for Open Loop 1 (OL1)
30
25
Magnitude (dB)
20
15
10
5
G.M.: Inf
Freq: NaN
Stable loop
0
-5
0
Phase (deg)
-45
-90
-135
P.M.: 92.9 deg
Freq: 7.95e+003 Hz
-180
1
10
2
3
10
10
4
10
Frequency (Hz)
Fig. 8.62 - Diagrama de Bode da FTMA da planta de controle em modo
corrente do conversor Boost sem compensação.
O diagrama de Bode da planta de controle com o controlador
PI+pólo ajustado é apresentado na Fig. 8.63. A margem de fase é de 88
graus com a frequência de cruzamento por zero do ganho em 2 kHz.
Foram avaliadas frequências de cruzamentos por zero do ganho em 10
kHz e 17 kHz, no entanto o desempenho transitório se mostrou instável
para ambas as condições, assim a frequência foi limitada no valor final
de 2 kHz.
Apostila de Controle de Conversores Estáticos
PPGEEL
220
Controle de Conversores
Open-Loop Bode Editor for Open Loop 1 (OL1)
40
20
Magnitude (dB)
0
-20
-40
-60
-80
G.M.: Inf
Freq: Inf
Stable loop
-100
Phase (deg)
-120
-90
-135
P.M.: 88.3 deg
Freq: 2e+003 Hz
-180
2
10
3
10
4
5
10
10
6
10
7
10
Frequency (Hz)
Fig. 8.63 - Diagrama de Bode da FTMA da planta de controle em modo
corrente do conversor Boost com compensação.
O controlador de tensão do controle em modo corrente é
representado no domínio da frequência pela equação (13.4), com os
coeficientes apresentados na Tabela 8.11. O circuito utilizado as
simulação do controle é apresentado na Fig. 8.64. A razão cíclica é
limitada em 0,6.
Tabela 8.11 – Coeficientes do controlador de tensão do controle em
modo corrente do conversor Buck.
Coeficiente
B2
B1
B0
A2
A1
A0
K
Valor
0
1
2561
1
5,026e5
0
125970
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
221
Fig. 8.64 - Circuito simulado no PSIM para avaliação do controle em
modo corrente do conversor Boost.
Na Fig. 8.65 é apresentado o resultado da tensão de saída para
uma variação de 15% na referência, a situação oposta é apresentada na
Fig. 8.36 onde a referência é aumentada em 15%. Nas duas figuras são
apresentadas também a tensão da saída do controlador e a corrente
medida no sensor. Nas duas situações observa-se que a tensão de saída
no início do transitório toma a direção oposta da referência, sendo este
um comportamento típico de uma planta que possui um zero no semiplanto direito, omitido na modelagem para controle em modo corrente.
Durante alguns instantes durante o transitório a razão cíclica é limitada
em 0,6 e não pela corrente.
Apostila de Controle de Conversores Estáticos
PPGEEL
222
Controle de Conversores
Tensão de Saída
Referência
Limite de corrente
Corrente no sensor
Fig. 8.65 - Quadro superior: Tensão de saída (vermelho) e referência
(azul).
Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para degrau de +15%.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
223
Referência
Tensão de Saída
Limite de corrente
Corrente no sensor
Fig. 8.66 - Quadro superior: Tensão de saída (vermelho) e referência
(azul)
Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para degrau de -15%.
Na Fig. 8.37 apresenta-se o resultado para uma referência
composta de um sinal CC de 400 V e uma componente senoidal de 60 V
com frequência de 1 kHz. A tensão de saída apresenta um atraso de 30
graus em relação a referência, além de uma atenuação.
Fig. 8.67 – Tensão de saída (vermelho) e referência senoidal de 1 kHz
(azul).
Apostila de Controle de Conversores Estáticos
PPGEEL
224
Controle de Conversores
Na Fig. 8.38 é apresentado o comportamento da tensão de saída e
da corrente de entrada (Isens) para uma redução de 50% na carga. Na
Fig. 8.39 é apresentado o comportamento da saída para um aumento de
carga de 50% para 100% da carga nominal. Nesta situação verifica-se o
comportamento adequado da tensão, sendo estabilizada em menos de
menos de 2 ms pelo controlador.
Tensão de Saída
Referência
Limite de corrente
Corrente no sensor
Fig. 8.68 – Quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para redução de carga de 50%.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
225
Referência
Tensão de Saída
Corrente no sensor
Limite de corrente
Fig. 8.69 – Quadro superior: Tensão de saída (vermelho) e referência
(azul) Quadro inferior: Corrente na saída do sensor (roxo) e limite do
controlador (verde) para aumentos de carga de 50%.
8.1.5
Conclusões
Neste capítulo foram aplicadas algumas técnicas de controla aos
conversores Buck e Boost operando no modo de condução contínua. A
planta do conversor Buck apresenta uma configuração de pólos e zeros
que a torna mais simples seu controle, além disso esta planta não
depende da variação da razão cíclica. A planta de tensão em relação a
razão cíclica do conversor Boost apresenta um zero no semi-plano
direito, o efeito deste zero pode ser verificado na dificuldade de controle
deste em relação ao Buck. Enquanto um Buck operando com razão
cíclica de 20kHz pode ter uma banda de controle de cerca de 5kHz a
banda do Buck operando em 70kHz teve uma banda de somente 100Hz,
considerando o mesmo controlador.
A alternativa de controle de tensão de saída via ajuste da corrente
no indutor foi explorada de duas maneiras, a primeira através do valor
médio e a segunda através do valor de pico. Nesta metodologia a
corrente de saída pode ser facilmente limitada através da inserção de
limitadores nas referências de corrente (isto foi implementado apenas no
controle em modo corrente). Com a metodologia do controle da corrente
Apostila de Controle de Conversores Estáticos
PPGEEL
226
Controle de Conversores
de pico no indutor pode-se obter o melhor resultado do controle de
tensão do Boost, o que ocorre devido a simplificação da planta de
corrente inerente a este método de controle.
A resposta do controle a grandes variações de carga está
relacionada a capacidade de armazenamento do capacitor de saída em
relação a carga. Operando no modo de condução contínua existe um
retardo no estabelecimento de uma nova corrente média no indutor,
assim durante este período o capacitor de saída terá que prover a energia
da carga através de sua descarga.
Apostila de Controle de Conversores Estáticos
PPGEEL
Controle de Conversores
Apostila de Controle de Conversores Estáticos
227
PPGEEL
228
Apêndice IV
Bibliografia
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
MEZAROBA,
M.,
http://www.joinville.udesc.br/portal/professores/mezar
oba/materiais/Modulacao_PWM.pdf, 2012.
PERIN, A. J., Modulação PWM Relatório Interno INEP/UFSC, 1998.
MARUYAMA, T.; KUMANO, M. New PWM Control
Method for a Three Level Inverter, 1991.
VELAERTS, B.; MATHYS, P., “New Development of
3-Level PWM Strategies”, in European Conference
Power Eletronics and Applications (EPE), 1989.
"Orcad Capture", 1998, p. Programa para Simulação de
Circuitos Eletrônicos Analógicos e Digitais.
MATSUI, K.; KAWATA, Y.; UEDA, F. Application of
Parallel Connected NPC-PWM Inverters with
Multilevel Modulation for AC Motor Drive. : IEEE
Transactions On Power Eletronics, September 2000.
FAR, Z. D.; RADAN, A.; FAR, M. D., Introduction
and Evaluation of Novel Multi-level Carrier-based
PWM Strategies Using a Generalized Algorithm, in:
European Conference on Power Electronics and
Applications, 2007., vol. 1, pp. 1-10, 2007.
HOLMES, D. G.; LIPO, T. A. Pulse Width Modulation
for Power Converters - Principles and Practice: A Jonh
Wiley & Sons, Inc., Publication, 2003.
ZARAGOZA, J.; POU, J.; CEBALLOS, S. et al., A
Comprehensive Study of a Hybrid Modulation
Technique for the Neutral-Point-Clamped Converter,
IEEE Transactions on Industrial Electronics, vol. 56,
n°. 2, pp. 294 - 304, Feb. 2009.
POU, J.; ZARAGOZA, J.; RODRIGUEZ, P. et al.,
Fast-Processing Modulation Strategy for the NeutralPoint-Clamped Converter With Total Elimination of
Alessandro Luiz Batschauer
Tese de Doutorado
Extra.....
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
229
Low-Frequency Voltage Oscillations in the Neutral
Point, IEEE Transactions on Industrial Electronics,
vol. 54, n°. 4, pp. 2288 - 2294, Aug. 2007.
CORZINE, K. A.; WIELEBSKI, M. W.; PENG, F. et
al., Control of Cascaded Multi-level Inverters, in: IEEE
International
Electric
Machines
and
Drives
Conference, IEMDC'03, vol. 3, pp. 1549 - 1555, 2003.
JINGSHENG, L.; CORZINE, K.; FERDOWSI, M., A
New Control Method for Single-dc-source Cascaded Hbridge Multilevel Converters Using Phase-shift
Modulation, in: Twenty-Third Annual IEEE Applied
Power Electronics Conference and Exposition, APEC
2008, vol. 1, pp. 886 - 890, 2008.
MARIETHOZ, S.; RUFER, A., New Configurations for
the Three-phase Asymmetrical Multilevel Inverter, in:
IEEE 39th IAS Annual Meeting Industry Applications
Conference, 2004., vol. 2, pp. 828 - 835, 2004.
RECH, C., Análise, Projeto e Desenvolvimento de
Sistemas Multiníveis Híbridos. Santa Maria.
2005.Doutorado em Eng. Elétrica,Universidade Federal
de Santa Maria.
OGATA, K. Engenharia de Controle Moderno. 2nd Ed.
ed., Rio de Janeiro, 1993.
GONÇALVES, L. A. M., "Sistemas de Controle,
Analise e Projeto pela Teoria Convencional".
WIKIPEDIA.
"http://pt.wikipedia.org/wiki/Sistema_de_controle".
MIT,
P.
D.
E.
"http://stuff.mit.edu/afs/athena/course/2/2.010/www_
f00/psets/hw3_dir/tutor3_dir/tut3_a.html".
ELETRICA, D. D. E. "Projetos de Sistemas de Control
PUCRS".
BARBI, I. Projeto de Fontes Chaveadas. 2nd ed. ed.,
2007.
MATHWORKS, R. B. D. "Control System Toolbox".
Apostila de Controle de Conversores Estáticos
PPGEEL
230
[22]
[23]
[24]
[25]
[26]
Apêndice IV
BATSCHAUER, A., "Notas de aula da disciplina de
Controle de Conversores Estáticos", 2012.
BRUNING, C., Apostila Modelagem Conversor Boost,
2012.
BARBI;, I.; MARTINS, D. C. Conversores CC-CC
Básicos Não Isolados, 2000.
ERICKSON;, R.; MAKSIMOVIC, D. Fundamentals of
power eletronics. 2nd ed. ed., New York: Springer
Science, 2001.
KAZIMIERCZUK, K. M. Pulse-width Modulated DCDC Power Converters, Wiley, 2008.
Alessandro Luiz Batschauer
Tese de Doutorado