16ª aula

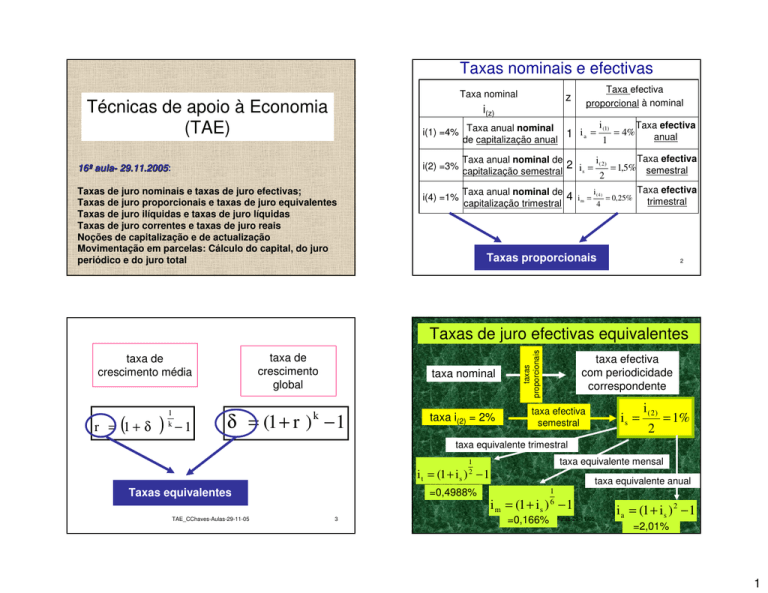
Taxas nominais e efectivas
Taxa nominal
Técnicas de apoio à Economia
(TAE)
Taxa efectiva
proporcional à nominal
z
i(z)
i (1)
Taxa efectiva
i(1) =4% Taxa anual nominal 1 i a =
= 4%
anual
de capitalização anual
1
16ª
16ª aulaaula- 29.11.2005:
29.11.2005
Taxas de juro nominais e taxas de juro efectivas;
Taxas de juro proporcionais e taxas de juro equivalentes
Taxas de juro ilíquidas e taxas de juro líquidas
Taxas de juro correntes e taxas de juro reais
Noções de capitalização e de actualização
Movimentação em parcelas: Cálculo do capital, do juro
periódico e do juro total
i(2) =3%
Taxa efectiva
Taxa anual nominal de
2 i s = i ( 2) = 1,5% semestral
capitalização semestral
2
i(4) =1%
Taxa efectiva
Taxa anual nominal de
4 i m = i (4) = 0,25% trimestral
capitalização trimestral
4
TaxasTAE_CChaves-Aulas-29-11-05
proporcionais
2
taxa de
crescimento
global
taxa nominal
δ = (1 + r ) − 1
taxa i(2) = 2%
taxa de
crescimento média
r = (1 + δ
)
1
k
−1
k
taxas
proporcionais
Taxas de juro efectivas equivalentes
taxa efectiva
com periodicidade
correspondente
taxa efectiva
semestral
is =
i ( 2)
2
= 1%
taxa equivalente trimestral
taxa equivalente mensal
1
2
i t = (1 + i s ) − 1
Taxas equivalentes
TAE_CChaves-Aulas-29-11-05
=0,4988%
3
1
6
i m = (1 + i s ) − 1
=0,166%
TAE_CChaves-Aulas-29-11-05
taxa equivalente anual
i a = (1 + i s ) 2 − 1
=2,01%
4
1
Exercício
Taxas de juro brutas e líquidas
i liq = i br ⋅ (1 − t imp )
Taxa de juro líquida
(após pagamento do
imposto)
Taxa de juro ilíquida
(antes pagamento
do imposto)
Taxa de imposto
Taxas de juro correntes e reais
1+ i
i =
−1
1 + δp
Deflação de taxas
de juro
r
Taxa de juro real
Taxa de
juro
corrente
Taxa de inflação
TAE_CChaves-Aulas-29-11-05
O Sr A efectuou, no início de 2003, um
depósito de 15 500 euros a uma taxa de
juro anual nominal de capitalização
semestral de 3%.
Sabendo que as taxas de inflação em
2003 e 2004 foram de 2,5% e 1,4%,
respectivamente, determine:
a)O valor da conta no final de 2004
b) O valor total de juros recebidos
c) A taxa de juro anual efectiva real em
cada ano.
5
TAE_CChaves-Aulas-29-11-05
Acumulação e actualização
C0
0
C 0 (1 + i) C 0 (1 + i) 2
1
1000 ⋅ (1 + 2%) −2 1000 ⋅ (1 + 2%) −1
= 961,17
= 980,39
actualização
1000
Movimentação de capital em parcelas
Cn = C0 (1 + i ) n
2
3
...
n
Exemplo: projecto de investimento em várias fases
• momento 0: realização dos cálculos
•momento 1: pagamento de 5000 u.m.
•momento 2: pagamento de 800 u.m.
•momento 5: recebimento de 6000 u.m.
•taxa de juro constante: 5%
•duração de 7 anos
5000
2
1000 ⋅ (1 + 2%) 1000 ⋅ (1 + 2%)
= 1020
TAE_CChaves-Aulas-29-11-05
6
= 1040,4
0
7
1
800
2
6000
3
4
5
TAE_CChaves-Aulas-29-11-05
?
6
7
8
2
5000
800
6000
1106,5
Cálculo do juro periódico do capital (dividido em parcelas)
2ª parcela
1ª parcela
0
1
2
3
4
5
6
0
1
2
3
4
5
6
7
7
capital em parcelas
0
1
2
3
4
5
6
7
1ª parcela
2ª parcela
5000
5250
5512,5
5788,13
6077,53
6381,41
6700,48
800
840
882
926,1
972,41
1021,03
parcela
subtraida
Capital
5000
6050
6352,5
6670,13
1003,63
1053,81
1106,50
-6000
-6300
-6615
Juro 1ª
5000
5250
5512,5
5788,13
6077,53
6381,41
6700,48
250
262,5
275,63
289,41
303,88
319,07
800
840
882
926,1
972,41
1021,03
J k = i ⋅ C k −1
J k = J k (1ª parcela ) + J k ( 2 ª parcela ) − J k ( parcela retirada )
TAE_CChaves-Aulas-29-11-05
9
TAE_CChaves-Aulas-29-11-05
C 7 = 5000(1 + 5%) 6 + 800(1 + 5%) 5 − 6000(1 + 5%) 2 = 1106,5
Cálculo do juro total do capital (dividido em parcelas)
0
1
2
3
4
5
6
7
Juro
Juro
Juro 1ª Juro 2ª subtraido
250
40
262,5
42
275,63
289,41 44,1
303,88 46,31
319,07 48,62
Total 1700,48 221,03
-615 1306,5
n
JTk =
250
302,5
317,63
333,51
-300 50,18
-315 52,69
Capital Juro
parcela Juro
Juro 2ª subtraida subtraido
5000
6050
250
6352,5 302,5
40
6670,13 317,63
42
1003,63 333,51
44,1
-6000
-6300
-300 1053,81 50,18
46,31
-315 1106,50 52,69
-6615
48,62
Cálculo do juro
total
n
JTk =
10
[
]
J = C k − C0 = C0 (1 + i) k − 1
k =1 k
= 5000 ⋅ 5% + 5000(1 + 5%) ⋅ 5% + ... + 5000(1 + 5%) 5 ⋅ 5%
+ 800 ⋅ 5% + 800(1 + 5%) ⋅ 5% + ... + 800(1 + 5%) 4 ⋅ 5%
− 6000 ⋅ 5% − 6000 (1 + 5%) ⋅ 5%
J
k =1 k
[
]
[
]
[
]
= 5000 ⋅ (1 + 5%) 6 − 1 + 800 ⋅ (1 + 5%) 5 − 1 − 6000 ⋅ (1 + 5%) 2 − 1
JT7 =
7
k =2
JT(1ª parcela)
= 5000 ⋅ 5% + 5000(1 + 5%) ⋅ 5% + ... + 5000(1 + 5%) ⋅ 5%
+ 800 ⋅ 5% + 800(1 + 5%) ⋅ 5% + ... + 800(1 + 5%) 4 ⋅ 5%
TAE_CChaves-Aulas-29-11-05
JT( parcela retirada)
= 5000 ⋅ (1 + 5%) + 800 ⋅ (1 + 5%) − 6000 ⋅ (1 + 5%) − (5000 + 800 − 6000)
Jk
5
− 6000 ⋅ 5% − 6000(1 + 5%) ⋅ 5%
JT( 2 ª parcela)
6
11
5
= C 7 + 6000 − (5000 + 800)
JTk =
2
C7
saídasTAE_CChaves-Aulas-29-11-05
de capital - entradas de capital12
3