Evolucao das ideias sobre o Universo e as forcas no Universo F12

3.2
Evolução das ideias sobre o Universo e
as forças no Universo
O modelo naturalista de Aristóteles
Desde o surgimento do Homo Sapiens, há cerca de 30 000 anos, que as
comunidades humanas mais evoluídas tentam compreender o Cosmos —
que é «tudo o que existiu, que existe e que existirá», na definição do
astrofísico norte-americano Carl Sagan.
No século IV a.C., Aristóteles (384-322 a.C.), filósofo grego, sistematizou os
conhecimentos da sua época. A sua visão do Universo traduz uma
perspectiva naturalista (ou seja, baseada na observação atenta da Natureza),
com um discurso de senso comum (ou senso do dia a dia). Acreditava num
Universo geocêntrico (geo = Terra, em grego), isto é, um Universo em que a
Terra estava no centro, e geoestático, quer dizer, a Terra estava parada.
Aristóteles (384-322 a.C.)
À volta da Terra, giravam os seis corpos celestes então conhecidos (Lua, Sol,
Vénus, Marte, Júpiter e Saturno), situados em esferas transparentes. E à volta
de todos, situava-se a esfera exterior, também transparente, a esfera das
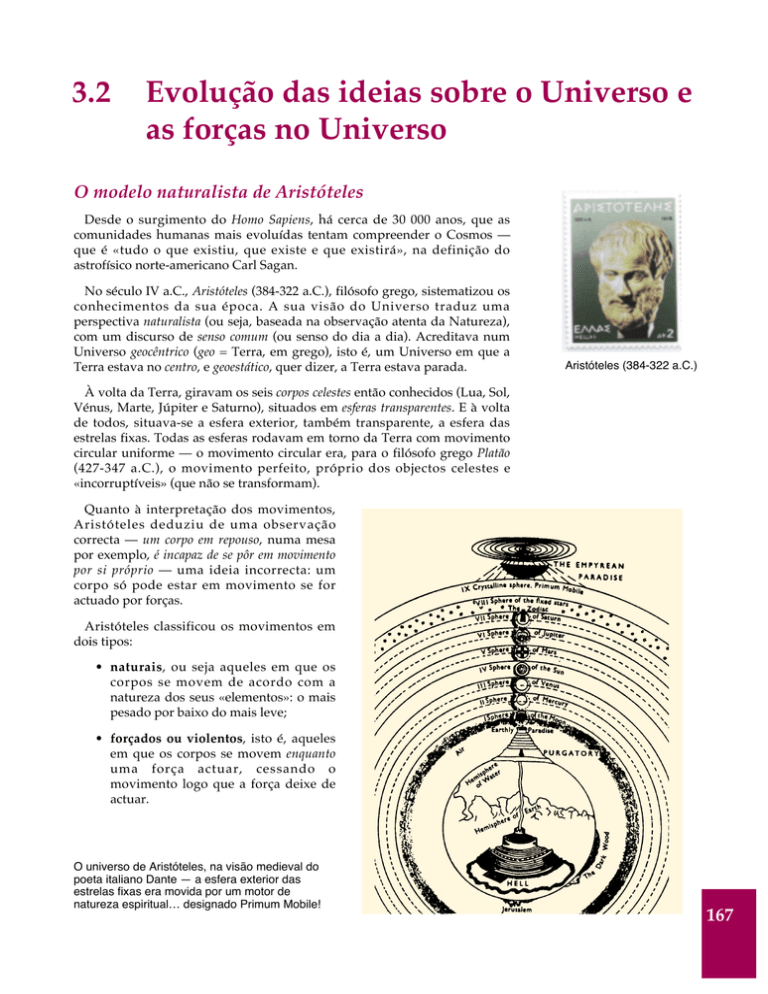
estrelas fixas. Todas as esferas rodavam em torno da Terra com movimento
circular uniforme — o movimento circular era, para o filósofo grego Platão
(427-347 a.C.), o movimento perfeito, próprio dos objectos celestes e
«incorruptíveis» (que não se transformam).
Quanto à interpretação dos movimentos,
Aristóteles deduziu de uma observação
correcta — um corpo em repouso, numa mesa
por exemplo, é incapaz de se pôr em movimento
por si próprio — uma ideia incorrecta: um
corpo só pode estar em movimento se for
actuado por forças.
Aristóteles classificou os movimentos em
dois tipos:
• naturais, ou seja aqueles em que os
corpos se movem de acordo com a
natureza dos seus «elementos»: o mais
pesado por baixo do mais leve;
• forçados ou violentos, isto é, aqueles
em que os corpos se movem enquanto
uma força actuar, cessando o
movimento logo que a força deixe de
actuar.
O universo de Aristóteles, na visão medieval do
poeta italiano Dante — a esfera exterior das
estrelas fixas era movida por um motor de
natureza espiritual… designado Primum Mobile!
167
Na cosmologia de Aristóteles, os corpos celestes não seriam formados por
nenhum dos chamados quatro elementos básicos (terra, água, ar e fogo),
transformáveis, mas por um elemento não transformável (ou incorruptível),
designado por «quinta essência». E os movimentos circulares dos objectos
celestes seriam, além de naturais, eternos…
Estes conceitos sobre objectos e movimento e algumas das suas
consequências, como, por exemplo, «os corpos pesados caem sempre mais
rapidamente do que os corpos leves», «o vazio não existe, porque a
Natureza tem horror ao vácuo», etc., perduraram até ao século XVII!
Deve-se ao italiano Galileu (1564-1642) a ultrapassagem de algumas
concepções aristotélicas. Galileu é um dos fundadores da ciência moderna: foi
com ele que as especulações científicas passaram a fundamentar-se na
observação, na experiência controlada, na concepção de experiências ideais
e na formulação de teorias.
O modelo ptolomaico do universo geoestático
Ptolomeu (90-168 d.C.), membro da escola de Alexandria (então
uma colónia grega no Egipto), matemático, astrónomo e
geógrafo, retomou, aperfeiçoou e desenvolveu a cosmologia
aristotélica. Ptolomeu condensou todo o conhecimento
astronómico dos gregos no célebre tratado Almagesto (esta
palavra significa «o muito grande» — de facto, a obra era, ela
própria, muito grande: 13 volumes!). Foi a «bíblia» dos
astrónomos até ao século XVI!
Como explicava Ptolomeu os movimentos dos astros? Em
particular, como explicava o movimento dos planetas? Os
planetas (palavra que significa errante) eram vistos a mover-se
ora num sentido ora no sentido contrário…
Ptolomeu criou um modelo segundo o qual os planetas
descreviam epiciclos. Estes resultavam de um movimento
uniforme ao longo de circunferências, movendo-se os centros
destas, por sua vez, sobre uma circunferência maior
1 de Dez.
planeta
epiciclo
Terra
deferente
Modelo de Ptolomeu para explicar as
«laçadas» dos planetas, observadas da
Terra.
1 de Jan.
1 de Maio
1 de Fev.
1 de Abril
1 de Nov.
1 de Out.
Posições do planeta Marte
em 1992-1993, face às
estrelas «fixas». As
«laçadas» descritas pelos
planetas intrigaram os
Antigos…
168
(deferente). Além desta hipótese, teve de acrescentar outras para explicar o
facto de os planetas não se moverem uniformemente. Para Ptolomeu, o seu
sistema era simplesmente um modelo do Universo e não, necessariamente,
uma representação verdadeira. Seguia o ideal grego de construir um
modelo que permitisse prever as observações astronómicas, naquele tempo
realizadas a olho nu…
Simulação computacional do
movimento de um planeta em
torno da Terra, segundo o
modelo de Ptolomeu. Neste
exemplo, o planeta descreve
sete epiciclos, dos quais seis
estão visíveis.
Pode perguntar-se: como é que um modelo tão complexo perdurou mais
de 13 séculos? Podemos indicar algumas razões.
A primeira é que o modelo estava em conformidade com o senso comum e
as concepções existentes. Por exemplo: a Terra está em repouso e todos os
outros astros giram em volta da Terra; os movimentos dos astros são
circulares, perfeitos; tudo o que existe foi feito para o ser humano
desfrutar…
A segunda é que o modelo permitia prever os movimentos celestes com
precisão suficiente para aquela época.
A terceira é que o modelo era flexível: permitia a introdução de novos epiciclos
e outros artifícios, se fosse necessário ajustá-lo a novas observações.
A Terra, centro imóvel do Mundo — uma ideia que foi
caindo…
Diagrama sobre a teoria de
Ptolomeu, num livro de 1472.
Ecfanto de Siracusa (séc. IV a.C.), discípulo de Pitágoras, Heráclides do Ponto
(séc. IV a.C.), da escola de Platão, em Atenas, e Aristarco de Samos (séc. III
a.C.), da escola de Alexandria, sugeriram que a Terra podia ter movimento de
rotação diário, em torno do seu eixo. Aristarco acrescentou mesmo que a
Terra também podia descrever, durante um ano, uma órbita em torno do
Sol. Estas ideias, porém, não vingaram — não estavam de acordo nem com
as ideologias nem com as religiões daquele tempo. Aristarco de Samos, o que
mais avançou, foi mesmo condenado depois de acusado de «impiedade!»
Todavia, à medida que as observações astronómicas aumentaram de
precisão — no século XV já se efectuavam com incerteza inferior a 10
minutos de grau! —, o modelo de Ptolomeu e a física de Aristóteles
depararam com dificuldades crescentes. A quantidade de epiciclos
acrescentados era tal que o rei de Leão e Castela, Afonso X, O Sábio, teria
comentado: «se Deus me tivesse consultado ao fazer o mundo, o resultado
não seria tão complicado!»… A partir de 1512, o monge e astrónomo polaco
Nicolau Copérnico (1473-1543) começou a defender um modelo helioestático
(hélio = Sol), que expôs na sua obra As Revoluções das Orbes Celestes,
publicada só em 1543, ano da sua morte… Neste modelo, os planetas
movem-se em torno do Sol, «fixo» na proximidade do centro da esfera das
estrelas fixas.
Nicolau Copérnico (1473-1543).
169
Tal como Ptolomeu, também Copérnico
explica os movimentos dos astros à custa
de epiciclos, embora em número menor.
Mas, no modelo de Copérnico, explicam-se
mais facilmente:
• a sucessão dos dias e das noites, uma
consequência do movimento de
rotação da Terra;
• a inversão do movimento dos
planetas sem ter de recorrer a
epiciclos.
Copérnico construiu a primeira escala das
distâncias dos planetas ao Sol, tomando para
unidade de medida a distância Sol-Terra, e
determinou o período de revolução de cada
planeta em torno do Sol. Os valores que
encontrou são próximos dos valores
actualmente aceites. Com os raios e os
períodos, conseguiu fazer previsões de posições futuras dos planetas.
Mas a física de Copérnico era ainda a física de Aristóteles. Por isso, não
pôde, por exemplo, responder satisfatoriamente às seguintes questões:
O sistema helioestático de
Copérnico tal como é
representado numa gravura da
época.
• Porque roda a Terra em torno do seu eixo? Argumentar que a rotação
é própria dos corpos esféricos não passa de uma forma de tornear a
questão, uma vez que não explica nada!
• Porque anda a Terra à volta do Sol? Afirmar que a translação ao
longo de uma circunferência é própria dos astros é também uma
maneira de fugir à pergunta.
• Porque motivo uma pedra abandonada do cimo de uma torre não vai
cair fora da base da torre? Então a terra em movimento não vai
fugindo por baixo do ponto de lançamento?
O modelo helioestático afirma-se com Kepler
Ainda no século XVI, o astrónomo dinamarquês Ticho Brahe (1546-1601) e
seus colaboradores determinaram, durante cerca de 20 anos, as coordenadas
dos astros com erros inferiores a dois minutos de grau! Foi uma autêntica
proeza com os meios de que dispunham. Com estes dados, surgiram
problemas que nem o modelo de Ptolomeu nem o modelo de Copérnico
conseguiram resolver.
Ticho Brahe era um sábio conservador e tentava conciliar os dois modelos,
uma síntese que se revelou impossível. Assim, aceitava que a Terra estivesse
fixa no centro do Universo e que os planetas girassem à volta do Sol, mas
punha este a rodar à volta da Terra… Não queria ferir a «majestade da
Terra»!
Giordano Bruno (1548-1600), padre e filósofo italiano, defendeu na altura
que o Universo era infinito e que a Via Láctea era formada por inúmeros
sóis, não havendo centro em parte alguma.
170
Ticho Brahe (1546-1601).
Bruno escreveu: «consideremos a evidência como prova do verdadeiro, e,
se a evidência falta, saibamos duvidar». Foi preso e julgado pela Inquisição,
em Roma, pois a Igreja interpretava à letra a descrição bíblica do Génesis, o
primeiro livro da Bíblia, como se nele estivessem escritas verdades
científicas. Giordano Bruno recusou-se a negar as suas convicções e a recuar
nas suas afirmações: foi queimado na fogueira…
Urgia resolver o «puzzle» da harmonia do Sistema Solar. Essa tarefa foi
levada a cabo pelo físico e astrónomo alemão Johannes Kepler (1571-1630).
Discípulo de Ticho Brahe, Kepler analisou os dados coligidos por este,
exaustiva e… pacientemente, pois nesse tempo não dispunha nem de
calculadoras nem de computadores!
As leis de Kepler
Desta sua análise persistente, Kepler induziu as três leis que sintetizam os
movimentos do Sistema Solar. As duas primeiras foram publicadas em 1609
e a terceira em 1618. Essas três leis são as seguintes:
1.a Lei das órbitas
Sol
A
semi-eixo menor
Cada planeta descreve uma órbita elíptica na qual um dos focos é ocupado pelo
Sol:,
C
As órbitas no Sistema Solar são
elipses de pequena excentricidade (a
excentricidade, e, mede a distância de
um foco ao centro, tomando para
unidade de comprimento o semi-eixo
maior: e = AC/CD, na figura). As
órbitas dos planetas são, pois,
praticamente, circunferências.
Simulação computacional do Sistema
Solar, à escala, entre 1 de Outubro de
1996 e quase um ano depois. Com
excepção de Mercúrio e Plutão, os
planetas do Sistema Solar têm órbitas de
pequena excentricidade — praticamente
circunferências.
planeta
semi-eixo maior
B
Um processo simples de
desenhar uma elipse: o bico
do lápis descreve uma elipse
se o fio se mantiver esticado.
Os pregos indicam a posição
dos dois focos da elipse. O
centro da elipse está na
posição intermédia entre os
dois focos.
D
Terra
Júpiter
Mercúrio
Sol
Vénus
Marte
171
2.a Lei das áreas
O vector-posição, que vai do Sol ao planeta, varre áreas iguais em intervalos de
tempo iguais:
∆t2 = ∆t1
∆t1
planeta
Software para computadores
IBM compatíveis:
∆t2
Kepler (exploração das leis da
gravitação).
Sol
Editor: SoftCiências (Projecto conjunto
das Sociedades Portuguesas de Física,
Química e Matemática), Dep. Física,
Faculdade de Ciências e Tecnologia,
3000 COIMBRA.
Desta lei conclui-se que o valor da velocidade do planeta é tanto maior
quanto mais perto o planeta estiver do Sol, porque percorre arcos cada vez
maiores no mesmo tempo. A velocidade tem, pois, o valor
quadrado do período, T2 (ano2 )
máximo no periélio (per = perto + hélio = Sol) e o valor mínimo
1000
no afélio (af = longe + hélio = Sol).
3.a Lei dos períodos
T
a
3
B Júpiter
100
Os quadrados dos períodos de revolução (T 2) são proporcionais aos
cubos dos semi-eixos maiores das órbitas (a3):
2
10
B Marte
1
= constante
B
0.1
Esta lei aplica-se a todos os planetas do Sistema Solar, assim
como aos satélites de Júpiter, descobertos por Galileu, e aos
demais satélites dos diversos planetas. O valor da constante é
diferente para cada caso (depende do astro com maior massa,
em cada sistema).
172
B
Saturno
B Terra
Vénus
B Mercúrio
0.01
0.01
Planeta
Período, T (em anos)
Semi-eixo maior, a (em UA)
Mercúrio
0,24
0,39
Vénus
0,61
0,72
Terra
1,00
1,00
Marte
1,88
1,52
Júpiter
11,86
5,20
Saturno
29,46
9,54
0.1
1
10
100
1000
cubo do semi-eixo maior, a3 (UA3 )
Representação da
proporcionalidade directa entre
os quadrados dos períodos de
revolução e os cubos dos
semi-eixos maiores das
órbitas, num gráfico de escalas
logarítmicas.
UA é a unidade astronómica,
distância média da Terra ao Sol.
A contribuição de Galileu
Galileu, contemporâneo e correspondente de Kepler, aderiu calorosamente
ao modelo de Copérnico-Kepler, só não aceitando as órbitas elípticas,
porque não estavam de acordo com a circunferência, a tal linha «perfeita»
que devia ser seguida pelos corpos celestes… Um resíduo das ideias antigas,
de que não se conseguiu libertar!
O entusiasmo de Galileu aumentou quando, a partir de 1609, passou a
utilizar sistematicamente o telescópio, através do qual pôde observar as
montanhas da Lua, os quatro satélites de Júpiter, as fases de Vénus
(semelhantes às da Lua), as manchas solares (afinal, o Sol não era um
objecto celeste perfeito), etc.
Galileu Galilei (1564-1642)
Galileu, apesar da sua amizade com o Papa Urbano VIII, também foi
julgado pela Inquisição em 1632, sendo obrigado a renunciar publicamente
às suas ideias. Com 68 anos e fragilizado, conhecedor do que sucedera a
Giordano Bruno, cedeu à exigência do tribunal, tendo-lhe sido então
imposta prisão domiciliária. Em 1979, o Papa João Paulo II reabilitou
publicamente Galileu.
Foi em casa e após o julgamento que o físico Galileu, quase cego e
acompanhado apenas por alguns discípulos, concluiu a sua obra científica
principal: estabeleceu a lei da queda dos graves, combinou a dedução lógica
com a indução experimental, sujeitou os dados à análise matemática, etc. E
para descrever o movimento acelerado, «esse movimento que a Natureza
utiliza», escolheu a aceleração e não a velocidade como o conceito mais
adequado. Com Galileu nasceu uma nova física. Mas não chegou à
gravitação, porque ainda não estava na hora!
Escolher entre o modelo de Ptolomeu e o modelo de Copérnico-Kepler foi
durante algum tempo uma questão de simples preferência. Mas, depois de
Galileu, a opção pelo modelo heliocêntrico tornou-se uma necessidade
intelectual. A evidência experimental a favor do modelo de CopérnicoKepler foi-se acumulando de forma impressionante.
O telescópio,
instrumento
aperfeiçoado por Galileu,
desempenhou um papel
fundamental nas suas
descobertas.
À esquerda: capa do livro
Diálogo dos Dois Grandes
Sistemas do Mundo, de
Galileu. Este livro foi
escrito na forma de
diálogo entre três
personagens; duas delas,
Simplício e Salviatti,
representam,
respectivamente, as ideias
de Aristóteles e Galileu. A
terceira, Sagredo, é um
leigo interessado.
À direita: manuscrito de
Galileu representando as
diferentes posições dos
satélites de Júpiter mais
próximos, numa série de
observações com o
telescópio.
173
3.3
A teoria newtoniana da gravitação
Vamos apresentar, esquematicamente, uma sequência lógica dos passos
que conduziram à lei da gravitação universal de Newton. Trata-se da
sequência lógica e não da sequência histórica, porque nesta houve
aproximações e erros, avanços e recuos. Segundo a lenda, foi uma maçã que
viu cair de uma árvore, quando tinha 23 anos, que fez despertar em Newton
as suas ideias…
Uma coisa é segura: não havia explicação dos movimentos no Sistema
Solar mas, sim e apenas, uma descrição. Quem a concebeu foi Newton, que
nos legou um produto final elegante — a sua Mecânica, sistematizada na
obra Princípios Matemáticos da Filosofia Natural, publicada em 1687. Filosofia
Natural era o estudo dos fenómenos da Natureza.
A força central…
Ao confrontar a lei das órbitas dos planetas, descoberta por Kepler, com a lei
da inércia, a 1.a lei do movimento formulada por ele próprio, Newton inferiu:
se um planeta descreve uma órbita elíptica, actua nele uma força. Esta
força devia ser central, isto é, devia estar permanentemente dirigida para um
ponto fixo (ou centro).
planeta
Sol
A força central actua continuamente. Para analisar o movimento do planeta,
Newton considerou intervalos de tempo a tender para zero (∆t → 0). Para
isso, utilizou o Cálculo Infinitesimal, que ele próprio inventou — ver
Manual de Actividades.
Newton concluiu também que, sendo os corpos actuados por forças centrais,
movem-se de acordo com a lei das áreas, a 2.a lei de Kepler.
174
Isaac Newton (1643-1727).
Às datas do calendário
gregoriano (ou Novo Estilo)
correspondem outras datas do
calendário juliano (ou Velho
Estilo), que diferem de 11 dias.
Como a Inglaterra só adoptou
o novo calendário em 1752 e
Newton nasceu a 5 de Janeiro
de 1643, segundo o calendário
novo, e a 25 de Dezembro de
1642, segundo o calendário
antigo, alguns livros indicam o
ano de nascimento pelo
calendário antigo.
Qual é a força central que actua nos planetas?
r
v
Nos seus primeiros estudos, Newton começou por considerar
órbitas circulares. Elas são uma aproximação razoável às
órbitas elípticas no Sistema Solar, dada a pequena
excentridade das órbitas planetárias, e são mais simples.
Mais tarde, utilizando o Cálculo Infinitesimal, mostrou
que os resultados obtidos se mantinham no caso de
órbitas elípticas quaisquer.
m
r
ac
Suponhamos então que um planeta, de massa m,
descreve uma órbita circular, de raio r, em torno do
Sol, com movimento uniforme (m.c.u.). Assim, quer a
força gravitacional quer a aceleração são centrípetas.
Como vimos na Unidade 2 e no 10.° ano, num m.c.u. o
valor da aceleração é dado por:
ac =
ac =
v2
r
v2
r
A esta aceleração corresponde, pela 2.a lei do movimento,
uma força centrípeta de valor:
Fg = m ac
=m
v2
r
m
Sendo T o período do m. c. u. planetário (tempo que
o planeta demora a dar uma volta completa em torno
do Sol), o valor da sua velocidade será
distância percorrida numa volta completa 2 π r
v=
=
período de revolução
T
r
Fg
Fg = m
v2
r
Substituindo o valor de v na equação da força, vem:
 2 π r


 T 
Fg = m
r
2
4 π2 r2
=m
=
T2
r
4 π2m r
T2
Esta equação aplica-se a qualquer m.c.u. Num m.c.u., a força é
directamente proporcional à massa m e ao raio da trajectória, r, e é
inversamente proporcional ao quadrado do período de revolução, T.
Newton recorreu então à lei dos períodos de Kepler,
T2
r
3
=C
ou
T 2 = C r3
175
onde C é uma constante que depende apenas do astro-central (ou
astro-director) — o Sol para os planetas, Júpiter para os seus satélites, a
Terra para a Lua, etc.
Substituindo T 2 na equação da força, obtemos:
Fg =
=
4 π2 m r
C r3
4 π2 m
C r2
Podemos definir um nova constante, KS = 4π2/C, e escrever, finalmente:
Fg = KS
m
r2
Newton concluiu, então, que a força gravitacional exercida pelo Sol sobre
qualquer planeta é:
• directamente proporcional à massa m do planeta;
• inversamente proporcional ao quadrado da distância r do planeta ao
Sol;
A constante de proporcionalidade KS tem a ver com o Sol. Por isso se usou
o índice S.
r
F4
r3
r4
r
F3
r
F2
r2
r1
Sol
planeta
r
F1
A força gravitacional, exercida pelo
Sol sobre qualquer planeta, é
directamente proporcional à massa,
m, do planeta e inversamente
proporcional ao quadrado da
distância, r, do planeta ao Sol.
Finalmente, o grande salto!
Subsistia, porém, uma questão: esta força que o Sol exerce nos planetas
terá a mesma natureza da força exercida pela Terra sobre a Lua? Terão estas
forças a mesma natureza da força que a Terra exerce sobre um objecto que
cai para a Terra? É aqui que entra a lenda da maçã…
176
Era necessário um «salto» corajoso: «saltar» dos corpos celestes para os
corpos terrestres. Newton teve a coragem de dar esse «salto», afirmando
que a força da gravidade terrestre, que atrai uma simples maçã, se estende
até à Lua e «obriga» esta a gravitar à volta da Terra. Do mesmo modo,
afirmou que a gravidade do Sol «obriga» a Terra e os outros planetas a
gravitarem à sua volta. Era uma hipótese que precisava de ser testada.
O teste de Newton
Newton pôde testar a sua ideia, conhecendo apenas a aceleração da
gravidade na Terra, a distância Terra-Lua e o período de revolução da Lua
— tudo dados conhecidos no seu tempo. Assim:
• aceleração da gravidade na Terra = 9,8 m/s2 ;
• distância Lua-Terra = 60 raios terrestres = 60 × 6,37 × 106 m = 3,82 × 108 m;
• período de revolução da Lua = 27,3 dias = 2,36 × 106 s.
De acordo com Newton, a força exercida pela Terra sobre qualquer corpo,
de massa m e à distância r do centro da Terra, tem o valor
m
Fg = KT
Terra
r2
onde KT é uma constante, que só depende da Terra, o astro-central. A esta
força corresponde a aceleração de valor:
Fg
a=
r
F
m
= KT
1
(1)
r2
A aceleração da Lua, aL, é então:
r
v
1
aL = KT
rL
Lua
2
Como rL = 60 rT , a aceleração da Lua, na sua «queda contínua» para a
Terra, é dada por:
aL = KT
1
(60 rT )2
= KT
=
Que relação há
entre a queda da
maça à superfície da
Terra e a «queda»
da Lua?
1
3600 rT 2
1
1
× KT × 2
3600
rT
Aplicando a equação (1) ao caso de um corpo M (por exemplo, a maçã…)
à superfície da Terra, vem:
a M = KT
1
rT 2
Dividindo aL por aM, temos:
aL
aM
1
1
× KT × 2
3600
rT
=
1
KT × 2
rT
177
Simplificando, obtém-se:
aL
1
=
a M 3600
ou
aL =
1
aM
3600
Quer dizer: o valor da aceleração da Lua em torno da Terra devia ser 3600
vezes menor do que o valor da aceleração da maçã à superfície da Terra. Ou
seja, a aceleração da Lua devia ser:
aL =
1
× 9, 8 m/s 2 = 2, 72 × 10 -3 m/s 2
3600
Como confirmar esta previsão? Basta calcular a aceleração centrípeta da
Lua, tendo em conta o seu período de revolução e a distância à Terra:
aL =
vL 2
rL
 2 π rL 


 T 
=
rL
=
2
4 π 2 rL
T2
Substituindo os dados, vem:
aL =
=
4 π 2 rL
T2
4 × 3, 14 2 × 3, 82 × 10 8
6 2
(2, 36 × 10 )
O valor da aceleração da Lua, no seu
movimento em volta da Terra, é
1/3600 do valor da aceleração da
maçã quando cai à superfície da
Terra.
= 2, 70 × 10 −3 m/s 2
um valor muito próximo do anterior.
A hipótese acerca da natureza idêntica das forças sobre os corpos à
superfície da Terra e sobre a Lua passou no teste e Newton pôde então
concluir:
A força que mantém a Lua na sua órbita é da mesma natureza da
força que a Terra exerce sobre os corpos terrestres. A força que o Sol
exerce sobre os planetas é ainda da mesma natureza.
Chamou-lhe força de gravitação universal.
178
E, a culminar, a lei!
Decorreram 21 anos entre os primeiros trabalhos científicos de Newton,
em 1666, e a publicação dos seus Princípios. O 3.° tomo, intitulado O Sistema
dos Mundos, é o primeiro grande tratado de Mecânica Celeste. O raciocínio
do seu autor deve ter sido o seguinte.
A força gravítica exercida por um astro, como o Sol, sobre um planeta de
massa m, à distância r, é uma força central inversamente proporcional ao
quadrado da distância, ou seja
Fg = K
m
r2
A constante K depende da massa do Sol. Pela lei da acção-reacção, actua
uma força simétrica no Sol (o planeta também atrai o Sol). Estas duas forças
simétricas dependem, por isso, das massas do Sol e do planeta, bem como
da distância entre eles. E, assim, Newton deu o «salto» final, que traduziu
no enunciado seguinte, também conhecido por lei da atracção universal ou
lei da gravitação universal:
Dois corpos quaisquer, no Universo, exercem entre si forças cuja
intensidade é directamente proporcional ao produto das suas
massas e inversamente proporcional ao quadrado da distância entre
eles.
Representemos agora a massa do planeta por m 2 e a massa do
astro-central por m 1 . A constante K, porque depende da massa do
astro-central, será K = G m1, onde G é a constante de gravitação universal.
Escreve-se, finalmente:
Fg = G
m1 m2
r2
Podemos também escrever as forças de gravitação recíprocas entre dois
astros
sob a forma vectorial. Para isso, utilizamos o versor (vector unitário),
r
e , na direcção da recta que passa pelo corpo de massa m1 e pelo corpo de
massa m2, e a apontar para fora:
r
m m r
F12 = G 1 2 2 e
r
e
r
m m r
F21 = − G 1 2 2 e
r
A lei da atracção universal contribuiu para alterar o modo
de pensar o Universo. A Terra deixou de ser vista como o
centro do Universo. Foram eliminados os «privilégios» de
alguns corpos celestes: todos os corpos do Universo
obedecem à lei da atracção universal.
m2
r
m1
r
e
r
F21
r
F12
179
A constante de gravitação universal
A constante de gravitação universal, G, é uma das constantes da Natureza,
tal como a velocidade da luz no vácuo. O seu valor foi estimado por Newton,
a partir de um valor aproximado da densidade da Terra e do raio médio da
Terra. A densidade média da Terra foi estimada em 5,0 g/cm3 = 5,0 × 103
kg/m3, que é um valor pouco diferente do actualmente conhecido. Para o
raio da Terra, tomou um valor próximo do actualmente aceite: rT =6,37×106 m.
Considerando a Terra uma esfera, o seu volume é dado por:
V=
=
4
π rT 3
3
4
× 3, 14 × 6, 37 × 10 6
3
(
)
3
(SI)
= 1, 08 × 10 21 m 3
Tendo em conta a densidade média da Terra, a massa da Terra é:
mT = densidade da Terra × volume
= 5, 0 × 10 3 × 1, 08 × 10 21
(SI)
= 5, 4 × 10 24 kg
A força gravítica exercida sobre um corpo à superfície da Terra é Fg = m g.
Comparando as duas fórmulas para calcular a força gravítica exercida
sobre um objecto de massa m, à superfície da Terra, vem:
mg =G
mT m
rT 2
Resolvendo esta equação em ordem a G, e substituindo valores, obtém-se:
G=
=
g rT 2
mT
(
9, 8 × 6, 37 × 10 6
5, 4 × 10 24
)
2
(SI)
= 7 , 4 × 10 −11 m 3 s −2 kg ±1
Este valor é da ordem de grandeza do valor experimental actualmente aceite,
G = 6,67 × 10–11 m3 s–2 kg–1
A constante G também pode exprimir-se nas unidades N m2 kg–2 , uma
vez que 1 N = 1 m s–2 kg e, portanto:
1 m3 s–2 kg–1 = 1 (m s–2 kg) m2 kg–2 = 1 N m2 kg–2
180
Newton estimou o valor da
constante de gravitação
universal a partir da estimativa
da densidade da Terra,
utilizando o valor do raio da
Terra, já conhecido na altura.
A balança de Cavendish ou… balança «pesa-mundos»!
O físico britânico Henry Cavendish (1731-1810), no final do século
XVIII, cerca de 100 anos após a publicação dos Princípios, mediu
experimentalmente a constante de gravitação universal, G.
Cavendish utilizou um dispositivo que é conhecido por balança
de torção.
A fotografia ao lado mostra uma balança de torção, semelhante à
usada por Cavendish, mas utilizando tecnologia actual. A balança
é constituída por duas esferas pequenas, fixas nas extremidades
de uma barra horizontal, suspensa de um fio comprido e fino. Este
fio torce-se devido à interacção gravitacional entre as esferas
pequenas e as esferas grandes. O raio laser e o espelho permitem
medir o ângulo de torção.
Para determinar o valor de G, mede-se:
• a distância r entre as esferas de tamanho diferente, de massas m1 e m2,
quando o binário das forças atractivas equilibra o binário de torção
do fio;
• a intensidade da força necessária, F, para produzir a torção de um
ângulo α, o ângulo correspondente à distância r;
• o valor das massas m1 e m2.
A interacção gravitacional
entre as esferas grandes e as
esferas pequenas torce um fio
do qual estão suspensas. O
ângulo de torção é
determinado a partir do ângulo
de rotação do espelho, ligado
ao fio e à barra, desviando um
raio laser.
Resolvendo em ordem a G a equação que traduz a lei da gravitação
universal
F=G
m1 m2
r2
obtém-se:
G=
F r2
m1 m2
α
Todas as variáveis do lado direito desta equação são determinadas
experimentalmente. O valor de G que Cavendish obteve era da mesma
ordem de grandeza do valor que tinha sido proposto por Newton, o que
confirmou a validade da lei da atracção universal.
O valor da constante de gravitação foi utilizado no século XVIII para
determinar a massa da Terra, sem necessidade de estimar a sua densidade.
Para tal, aplicou-se a equação que traduz a lei da gravitação universal para a
força de atracção entre um corpo de massa conhecida e a Terra, quando o
corpo se encontra à superfície da Terra. Considerando um corpo de massa
1,0 kg (o raio da Terra é 6,37 × 106 m), vem:
F=G
mT m
r2
9, 8 = 6, 67 × 10 −11
mT 1, 0
6 2
(6, 37 × 10 )
mT = 5, 96 × 10 24 kg
(SI)
181
Mais ainda: o valor da constante de gravitação permitiu também calcular
a massa do Sol, assim como a de qualquer planeta, desde que se
conhecessem o raio da órbita e o período de revolução da Terra ou de
qualquer outro planeta em torno do Sol! Recordamos que Copérnico já tinha
estabelecido uma escala de distâncias no Sistema Solar, tomando a distância
Terra-Sol como unidade, e já conhecia os períodos de revolução dos
principais planetas.
Considerando, com razoável aproximação, que o movimento de um
planeta em torno do Sol segue uma trajectória circular, a força centrípeta
responsável por esse movimento é a força gravitacional:
Fc = Fg
Como a aceleração centrípeta pode ser calculada pelo quociente v2/r,
temos, para um planeta de massa m:
m
mm
v2
=G 2S
r
r
Uma vez que o valor da velocidade v do planeta pode ser calculado tendo
em conta a distância percorrida numa revolução (2 π r) e o tempo que
demora (isto é, o período T do planeta), vem:
 2 π r


 T 
m
r
2
=G
m mS
r2
Simplificando esta equação e resolvendo-a em ordem à massa do Sol,
obtemos, sucessivamente:
4 π2 r2
T2
r
4 π2 r2
2
T r
4 π2 r
T2
=G
mS
=G
mS
=G
mS
mS =
r2
r2
r2
4 π2 r3
GT2
Quer dizer: para calcular a massa do Sol, basta conhecer a
distância r de qualquer planeta ao Sol, o respectivo período
de revolução T e, claro, a constante de gravitação G. Nem
sequer é necessário conhecer a massa da Terra ou de
qualquer planeta… A medida de G na balança de torção
permitiu, portanto, conhecer quer a massa do Sol quer a
massa da Terra. Foi por isso que alguém com humor deu à
balança de Cavendish o nome pitoresco de «balança
pesa-mundos»!
É fácil «pesar» o Sol… com a lei da gravitação!
182
Êxitos e limitações da teoria newtoniana
da gravitação
A teoria de Newton teve êxitos após êxitos desde o século
XVII até ao final do século XIX. Entre esses êxitos conta-se a
explicação das marés (devidas às forças de gravitação entre a
Terra e a Lua, principalmente), a explicação da precessão dos
equinócios e a previsão das órbitas dos cometas — ver
Manual de Actividades.
Foi também graças à teoria da gravitação universal que se
previu a existência de mundos… antes de serem descobertos. Foi o que
sucedeu com o planeta Neptuno, cuja existência foi prevista (devida à
interacção gravitacional com outros planetas) antes de ser observado em
1846. Foi também deste modo que se previu a existência de Plutão (em
1930), o planeta do Sistema Solar mais afastado do Sol. Quando os
astrónomos apontaram os telescópios para os sítios indicados pelos cálculos,
os planetas estavam «lá»!
Neptuno, um planeta
descoberto antes de ser visto,
graças à lei da gravitação
universal. Quando os
astrónomos apontaram os
telescópios para os sítios
indicados pelos cálculos,
encontraram-no «lá»!
Ainda hoje a lei da gravitação é muito utilizada. Por exemplo, com base
nesta lei calculam-se as órbitas dos satélites artificiais e fazem-se as
previsões dos eclipses e da passagem de cometas nas vizinhanças da Terra.
Apesar de todos estes sucessos, a lei da gravitação de Newton deixa
muitas questões por resolver. A primeira é que a lei da gravitação apenas
traduz o que se passa e como se passa, mas nada interpreta: é omissa quanto
ao porquê, isto é, nada diz quanto ao mecanismo do que se passa. Newton
sentiu este ponto fraco e chegou a admitir a existência de um «éter»,
preenchendo o espaço e desempenhando o papel de transmissor das forças
gravitacionais… Mas era uma afirmação que não podia demonstrar com
factos. E nada escreveu sobre esta hipótese…
Entre os problemas que nunca foram resolvidos com a teoria da
gravitação de Newton contam-se pequenas variações na órbita do planeta
Mercúrio, descobertas ainda no século XIX. Estes problemas só foram
resolvidos com a Teoria da Relatividade Geral, formulada por Einstein em
1916. Esta teoria, que descreve o campo de gravitação por «deformação do
espaço-tempo», tem sido confirmada em muitas situações. Um dos maiores
triunfos da teoria de Einstein foi a explicação do desvio dos raios luminosos
quando passam na vizinhança de uma estrela (a primeira verificação deste
facto foi realizada em 1919, numa expedição científica inglesa à ilha do
Príncipe, então uma colónia portuguesa na África Ocidental).
A Teoria da Relatividade Geral não veio invalidar,
de modo algum, a teoria newtoniana: é uma teoria
mais avançada e abrangente, que contém a teoria
newtoniana como caso particular.
A lei da gravitação é utilizada,
por exemplo, para prever as
trajectórias de satélites
artificiais e de naves espaciais.
183
Inércia e massa inercial, gravitação e massa
gravitacional
A massa inercial de um corpo é, como vimos no 11.° ano e na
Unidade 2 deste livro, a quantificação da sua inércia ou resistência
à mudança de velocidade. É medida pelo quociente
m=
r
a
m
Fres
a
r
Fres
Para medir a massa inercial de um corpo medem-se as forças aplicadas nele
e as acelerações que produzem no seu movimento. Como o quociente é
constante para cada corpo, deve dizer respeito a uma propriedade
característica desse corpo. Em particular, num corpo em queda livre, a força
que actua nele é a força gravítica, F g , e a aceleração com que cai é a
aceleração local da gravidade, g. Portanto a massa inercial é:
m=
Fg
r
g
m
g
r
Fg
Vimos também no 11.° ano e nas secções anteriores que a massa gravitacional de um corpo é a massa que «produz» e «responde» à força de
gravitação, de acordo com Newton. Quer dizer: é a propriedade do corpo
que aparece na lei da gravitação, expressa pela fórmula:
Fg = G
m mT
r2
Esta equação, resolvida em ordem a m, fica:
m=
Fg r 2
G mT
Como este quociente é constante para cada corpo, deve também dizer
respeito a uma propriedade característica desse corpo. Um modo prático e
simples de medir a massa gravitacional é o que recorre à balança de dois
pratos. Quando os dois corpos do lado direito ficam em equilíbrio com o
corpo do lado esquerdo (uma vez que são iguais, nesta situação, as forças
gravíticas que actuam em ambos os pratos da balança), a massa
gravitacional do corpo da esquerda é igual à soma das massas
gravitacionais dos objectos da direita (que são «massas marcadas» e
calibradas da caixa de massas).
184
Pois bem: todas as experiências feitas mostram que as medidas das duas
massas do mesmo corpo, a inercial e a gravitacional, são iguais! É um facto
algo desconcertante, por se tratar de propriedades de natureza diferente: a
inércia e a gravitação, respectivamente. Esta igualdade, notada por Newton,
foi verificada no início do século XX, com a precisão de 1 em 107 pelo físico
húngaro Roland Eötvös (1848-1919). A igualdade entre os valores da massa
inercial e da massa gravitacional impressionou fortemente Einstein e
conduziu-o ao chamado princípio da equivalência, no qual fundamentou a sua
Teoria da Relatividade Geral. Nesta teoria, a igualdade entre os valores da
massa inercial e da massa gravitacional é um ponto de partida essencial. Na
linguagem científica corrente, deixou de se distinguir entre massa inercial e
massa gravitacional. Fala-se simplesmente em massa.
m2
m1
Numa balança de pratos e
braços iguais, quando as
forças gravíticas se equilibram
a massa do corpo (m2) é igual
à soma das massas calibradas
(m1).