Baixar o arquivo

Lista de Exercícios - Aula 02
Terceira Lei de Newton
Diagramas do corpo livre: Equilíbrio Estático
1 – (Cap. 4 Ex 52 (a) pág 123 5a ed -Ex 52 pág 118 6a ed)
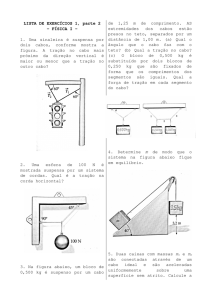
Para os sistemas em equilíbrio mostrados na figura abaixo,
determine as forças atrativas e a massa incógnita.
R – T1 = 60 N, T2 = 52 N e m = 5,3 kg
2 - (Sears & Zemansky –ex. 5.8 p.167) Uma bola grande de um guindaste de demolição é
mantida em equilíbrio por dois cabos de aço leves. Se a massa m da bola for igual a 4.090
kg, qual é :
a) a tração TB no cabo que faz um ângulo de 40º com
a vertical?
b) a tração TA no cabo horizontal?
3 - (R. C Hibbeler – Mecânica - Estática – Ex 3.17
p.28)(modificado) Determine a tração nos no cabo AB e no AC de
forma a sustentar um vaso de 6 kg.
4 - (Sears & Zemansky –ex. 5.4 p.167) Um homem passa de um
rochedo para outro se deslocando lentamente
com as mãos por meio de uma corda esticada
entre os rochedos. Ele para e fica em repouso
no meio da corda esticada. A corda se romperá
se a tensão for maior do que 2,50.104 N e se a
massa de nosso herói for maior ou igual a
90,0kg.
a se  = 100 qual é a tensão na corda?
b Qual deve ser o menor valor de  para a corda não se romper?
5 - (Sears & Zemansky –ex. 5.10 p.168) Um carro de massa 1130 kg está seguro por
um cabo leve, sobre uma rampa muito lisa (sem atrito), com indicado na figura. O cabo
forma um ângulo de 25º acima da horizontal.
a) Desenhe um diagrama do corpo livre par o carro.
b) Ache a tração no cabo.
c) Com que intensidade a superfície da rampa empura o carro?
7 - (R. C Hibbeler – Mecânica - Estática – Ex 3.27) A barra
de sustentação é usada para levantar um recipiente com massa
de 500 kg. Determine a força em cada um dos cabos AB e AC
em função de . Se a força máxima em cada cabo for 5 kN,
determine o menor comprimento do cabo AB e do AC que
pode ser usado para levantamento. O centro de gravidade do
recipiente está localizado em G.
R –  = 29,37 L = 1,72 m
8 - Determine a força F exercida pelo homem no fio para manter o
caixote na posição mostrada na figura abaixo. Encontre, também, a
tração T no fio superior (anterior à posição do gancho).
Diagramas do corpo livre: vários corpos
1 - (Cap. 4 Ex 69 pág 125 - Tipler 5a ed – Ex 67 pág121 6a ed) Uma caixa de massa
m2 = 3,5 kg repousa sobre uma estante horizontal sem
atrito, e é fixada através de cabos a duas caixas com
massas m1 = 1,5 kg e m3= 2,5 kg, penduradas livremente,
conforme mostrado na Figura abaixo. Ambas as roldanas
são consideradas sem atrito e sem massa. O sistema,
inicialmente, é mantido em repouso. Após ser liberado,
determine: a aceleração de cada uma das caixas e a força
de tração em cada cabo.
2 - (Cap. 4 Ex 70 pág 125 - Tipler 5a ed – Ex 68 pág 121 6ª ed) Dois blocos estão
em contato sobre uma superfície horizontal sem atrito. Os

blocos são acelerados através de uma força horizontal F
aplicada a um deles (Figura abaixo). Determine a
aceleração e a força de contato para para F = 3,2 N,
m1 = 2 kg e m2 = 6 kg.
Diagramas do corpo livre: plano inclinado
1 -(Cap. 4 Ex 57 pág 123 - Tipler)(modificado) Com
relação ao sistema mostrado na Figura:
a) se o sistema se encontra em equilíbrio, quanto vale a
massa m?
b) Considere a m = 4 kg, e que o bloco seja liberado do
repouso. Qual a velocidade com que o bloco de massa 3,5
kg atinge o solo?
2. (Tipler – 61 p.123) Ex 61. Um estudante de 65 kg deseja
medir seu peso ficando de pé sobre um skate que desce uma
rampa, conforme a figura. Admita que não haja atrito, de
modo que a força exercida pela rampa sobre o skate seja
normal à rampa. Qual é a indicação da balança para  = 300?
R - 552 N
3 - Um bloco de massa m = 20 kg desce um plano Inclinado sem atrito, sujeito a uma força
F que forma ângulo 35º com o plano inclinado como mostra a figura. Sendo F = 50
N, calcule o módulo da aceleração do bloco?
35o
22o