CENTRO DE MASSA 2.Cinco pontos materiais de massas

CENTRO DE MASSA
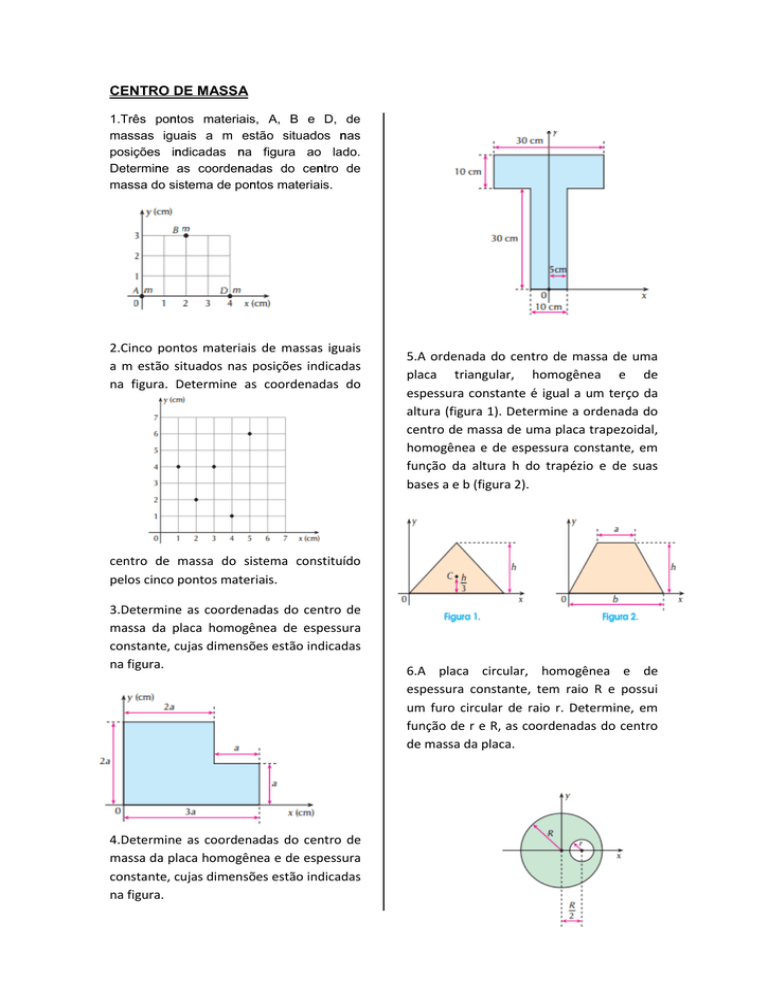
1.Três pontos materiais, A, B e D, de
massas iguais a m estão situados nas
posições indicadas na figura ao lado.
Determine as coordenadas do centro de
massa do sistema de pontos materiais.
2.Cinco pontos materiais de massas iguais
a m estão situados nas posições indicadas
na figura. Determine as coordenadas do
5.A ordenada do centro de massa de uma
placa triangular, homogênea e de
espessura constante é igual a um terço da
altura (figura 1). Determine a ordenada do
centro de massa de uma placa trapezoidal,
homogênea e de espessura constante, em
função da altura h do trapézio e de suas
bases a e b (figura 2).
centro de massa do sistema constituído
pelos cinco pontos materiais.
3.Determine as coordenadas do centro de
massa da placa homogênea de espessura
constante, cujas dimensões estão indicadas
na figura.
4.Determine as coordenadas do centro de
massa da placa homogênea e de espessura
constante, cujas dimensões estão indicadas
na figura.
6.A placa circular, homogênea e de
espessura constante, tem raio R e possui
um furo circular de raio r. Determine, em
função de r e R, as coordenadas do centro
de massa da placa.
7.Uma placa retangular de comprimento L
é constituída pela união de duas partes 1 e
2, como mostra a figura abaixo. A parte 1 é
feita de material de massa específica ρ1 e a
parte 2 de material de massa específica ρ2.
Suspendendo-se a placa pelo ponto P, de
acordo com a figura (AB horizontal), ela
permanece em equilíbrio. Sabe-se que
AP=2L/ 9 .
a) A que distância do lado AD
encontra-se o centro de massa da
placa?
b) Determine a razão ρ1/ ρ2 .
CONSERVAÇÃO DO MOMENTO LINEAR E IMPULSO
1-Dois blocos A e B, de massas mÛ = 0,2
2-Um patinador de 65 kg, em repouso,
kg e m½ = 0,8 kg, respectivamente, estão
arremessa
presos por um fio, com uma mola ideal
Horizontalmente para frente. A velocidade
comprimida entre eles. A mola comprimida
do peso em relação ao patinador é de 3,5
armazena 32 J
m/s no instante do arremesso. Calcule o
de
energia
potencial
um
peso
de
5,0
kg,
elástica. Os blocos estão inicialmente em
repouso, sobre uma superfície horizontal e
módulo da velocidade em relação à Terra,
lisa. Em um dado instante, o fio se rompe
adquirida
liberando os blocos. Calcule a velocidade
Despreze o atrito entre os patins e o piso.
do bloco A, em m/s.
pelo
patinador,
em
cm/s.
3-O número do homem-bala apresenta um
homem sendo disparado por um canhão.
Nesse circo, um macaquinho de 4,0kg
substitui o homem. Ele é disparado, com
uma velocidade inicial de 20m/s por um
canhão de 400kg, montado sobre rodas e
não freado, formando um ângulo de 60°
com a horizontal, conforme mostra a figura.
5-Dois patinadores, um de massa 100kg e
outro de massa 80kg, estão de mãos dadas
em repouso sobre uma pista de gelo, onde
o atrito é desprezível. Eles empurram-se
mutuamente e deslizam na mesma direção,
porém em sentidos opostos. O patinador de
100kg adquire uma velocidade de 4m/s. A
velocidade relativa de um dos patinadores
em relação ao outro é, em módulo, igual a:
a) 5 m/s
c) 1 m/s
e) 20 m/s
b) 4 m/s
d) 9 m/s
6- Uma pessoa pula de um muro, atingindo
4-Um corpo A com massa M e um corpo B
o chão, horizontal, com velocidade de
com massa 3M estão em repouso sobre
4,0m/s, na vertical. Se ela dobrar pouco os
um plano horizontal sem atrito como mostra
joelhos, sua queda é amortecida em 0,020s
a figura a seguir. Entre eles existe uma
e, dobrando mais os joelhos, consegue
mola, de massa desprezível, que está
amortecer a queda em 0,100s. Determine o
comprimida por meio de um barbante
módulo da força média da pessoa, em cada
tensionado que mantém ligados os dois
caso.
corpos. Num dado instante, o barbante é
cortado e a mola distende-se, empurrando
7-Na prova de resistência do pára-choques
as duas massas, que dela se separam e
de um novo carro, o veículo, de 2300 kg e
passam
livremente.
a 15 m/s, colide com o parapeito de uma
Designando-se por T a energia cinética,
ponte, sendo parado em 0,54 s. Determine
pode-se afirmar que:
a força média que atuou no carro o
a
se
mover
a) 9TÛ = T½
b) 3TÛ = T½
c) TÛ = T½
d) TÛ = 3T½
e) TÛ = 9T½
impacto.
8-O gráfico representa a força resultante
sobre um carrinho de supermercado de
massa total 40 kg, inicialmente em
repouso. aetermine A intensidade da força
constante que produz o mesmo impulso
que a força representada no gráfico
durante o intervalo de tempo de 0 a 25 s.
COLISÕES
1.A figura é uma representação de um
e prende-se à extremidade de uma mola de
pêndulo balístico, um antigo dispositivo
massa desprezível e constante elástica
para se medir a velocidade de projéteis.
igual a 9N/m. A outra extremidade da mola
está presa a um suporte fixo, conforme
mostra
a
Inicialmente
figura
a
(no
esfera
alto,
à
direita).
encontra-se
em
repouso e a mola no seu comprimento
natural. A esfera é então atingida por um
Suponha que um projétil com velocidade
pêndulo de mesma massa que cai de uma
Vp, de massa m = 10g, atinge o bloco de
altura igual a 0,5m. Suponha a colisão
massa M = 990g inicialmente em repouso.
elástica e g=10m/s£.
Após a colisão, o projétil aloja-se dentro do
bloco e o conjunto atinge uma altura
máxima h = 5,0 cm. Considerando g = 10
m/s2, determine a velocidade do projétil,
em m/s.
2.Uma esfera de massa igual a 100g está
sobre uma superfície horizontal sem atrito,
Calcule:
a) as velocidades da esfera e do pêndulo
imediatamente após a colisão;
b) a compressão máxima da mola.
3.Em um parque de diversões, dois
carrinhos elétricos idênticos, de massas
iguais a 150kg, colidem frontalmente. As
velocidades dos carrinhos imediatamente
antes do choque são 5,0m/s e 3,0m/s.
Calcule a máxima perda de energia cinética
possível do sistema, imediatamente após a
colisão.
4.Uma bola de tênis de massa m colide
inelasticamente contra uma parede fixa,
conforme é mostrado na figura a seguir. A
velocidade da bola imediatamente antes do
choque é perpendicular à parede e seu
módulo vale V³. Imediatamente após o
choque,
a
velocidade
continua
perpendicular à parede e seu módulo
passa a valer (2/3)V³.
Calcule em função de m e V³:
a) o módulo da variação do momento linear
da bola;
b) a variação de energia cinética da bola.
5.O pêndulo balístico é um sistema
utilizado para medir a velocidade de um
projétil que se move rapidamente. O projétil
de massa m• é disparado em direção a um
bloco de madeira de massa m‚,
inicialmente em repouso, suspenso por
dois fios, como ilustrado na figura. Após o
impacto, o projétil se acopla ao bloco e
ambos sobem a uma altura h.
a) Considerando que haja conservação da
energia mecânica, determine o módulo da
velocidade do conjunto bloco-projétil após o
impacto.
b) A partir do princípio da conservação da
quantidade de movimento, determine a
velocidade inicial do projétil.
6.Um carro A, de massa m, colide com um
carro B, de mesma massa m que estava
parado em um cruzamento. Na colisão os
carros se engastam, saem juntos,
arrastando os pneus no solo, e percorrem
uma distância d até atingirem o repouso,
como ilustram as figuras a seguir.
a) Calcule a razão EÝ'/EÝ entre a energia
cinética do sistema constituído pelos dois
carros após o choque (EÝ') e a energia
cinética do carro A antes do choque (EÝ).
b) Medindo a distância d e o coeficiente de
atrito de deslizamento ˜ entre os pneus e o
solo, conhecendo o valor da aceleração da
gravidade g e levando em consideração
que os carros tinham a mesma massa m, a
perícia técnica calculou o módulo vÛ da
velocidade do carro A antes da colisão.
Calcule vÛ em função de ˜, d e g.
RASCUNHO: