EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Esta aula:
Teorema de Thévenin,
Teorema de Norton.
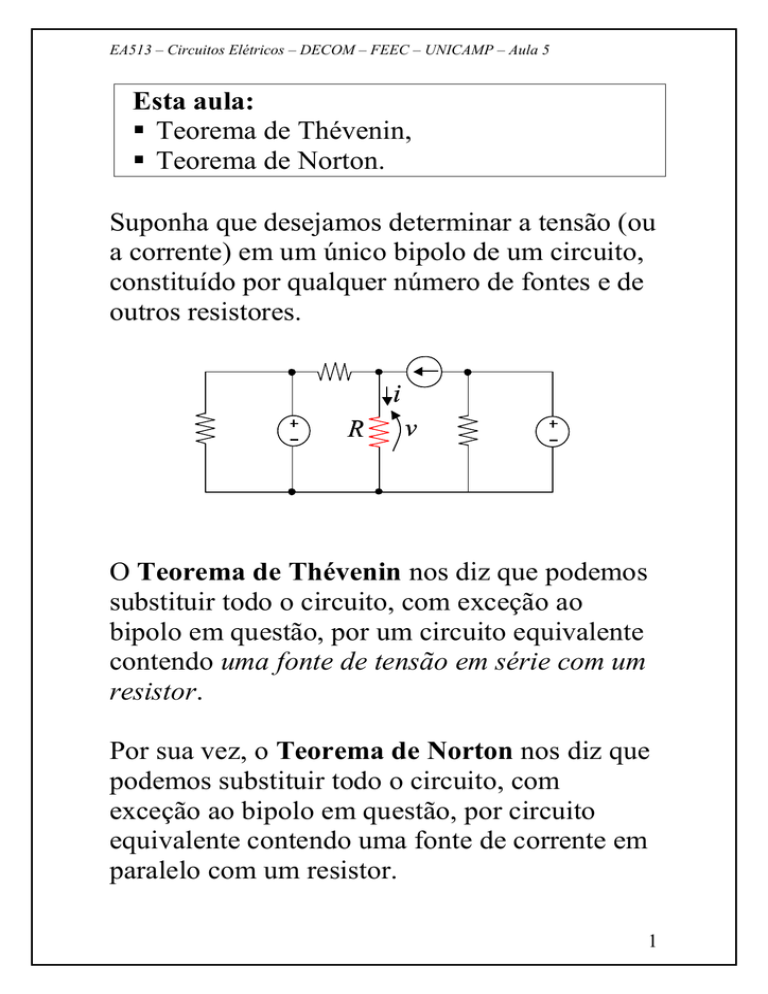
Suponha que desejamos determinar a tensão (ou
a corrente) em um único bipolo de um circuito,
constituído por qualquer número de fontes e de
outros resistores.
i
R
v
O Teorema de Thévenin nos diz que podemos
substituir todo o circuito, com exceção ao
bipolo em questão, por um circuito equivalente
contendo uma fonte de tensão em série com um
resistor.
Por sua vez, o Teorema de Norton nos diz que
podemos substituir todo o circuito, com
exceção ao bipolo em questão, por circuito
equivalente contendo uma fonte de corrente em
paralelo com um resistor.
1
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
i
R
v
Teorema de
Thevenin
vTh
RTh
Teorema de
Norton
i
R
i
v
iN
RN
v
R
2
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Consideremos um circuito elétrico que foi
rearranjado na forma de outros dois circuitos,
denotados por A e B.
Circuito A: deve ser um circuito linear:
fontes independentes,
bipolos lineares e
fontes dependentes lineares.
Circuito B: pode conter também elementos não
– lineares.
Restrição importante: Nenhuma fonte
dependente do circuito A pode ser controlada
por uma corrente ou tensão do circuito B e vice
versa.
Circuito
A
Circuito
B
Circuito
Equivalente
Thèvenin do
circuito A
Circuito
B
3
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Teorema de Thévenin:
Defina uma tensão vca como a tensão que
aparece nos terminais de A se o circuito B é
desconectado, de forma que nenhuma corrente
fluí do circuito A para o circuito B. Então, as
tensões e correntes em B permanecerão
inalteradas se desativarmos todas as fontes
independentes de A e uma fonte de tensão vca
for conectada em série com o circuito A
“desativado”.
Desativar fontes:
Substituir fontes independentes de corrente
por circuitos abertos,
Substituir fontes independentes de tensão
por curto-circuitos.
vcc
Circuito A
desativado
Circuito
B
Nenhuma fonte de
tensão ou corrente
4
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Teorema de Norton
Defina uma corrente icc como a corrente que
flui nos terminais de A se os pontos de conexão
entre A e B são curto-circuitados, de forma que
nenhuma tensão é fornecida por A. Então, as
tensões e correntes em B permanecerão
inalteradas se desativarmos todas as fontes
independentes de A e uma fonte de corrente icc
for conectada em paralelo com o circuito A
“desativado”.
Circuito A
desativado
icc
Circuito
B
Nenhuma fonte de
tensão ou corrente
Consideremos o circuito abaixo, para o qual
desejamos determinar os equivalentes de
Thévenin e de Norton sob o ponto de vista o
resistor R1 .
5
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
3k
2k
4V
R1 1k
2mA
Tensão em aberto:
2 k
4V
3k
i1
2mA
i1 2mA
vca vca 4 2 103 2 10 3
8V
Resistência do circuito desativado:
2 k
3k
5 k
Portanto, o circuito redesenhado com o
equivalente de Thévenin é:
6
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
5k
8V
R1 1k
Para construir o equivalente de Norton,
precisamos determinar a corrente de curtocircuito:
3k
2 k
icc
i2 i1 2
4V
i1
i2
4 2i1 3i2 0
2mA
i2 icc 1,6mA
Finalmente, o circuito com o equivalente de
Norton é:
1,6mA
5k
R1 1k
7
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Note que o equivalente de Norton pode ser
obtido a partir do equivalente de Thévenin (e
vice-versa) por meio de princípio da
equivalência entre fontes de tensão e de
corrente reais.
Consideremos agora um circuito com uma fonte
de corrente dependente linear, cujo equivalente
de Thévenin estamos interessados:
2 k
4V
3k
A
vx
4000
vx
B
Tensão em aberto:
A tensão de circuito aberto é a própria tensão de
controle da fonte de corrente, ou seja vca v x .
Então, aplicando a Lei de Kirchhoff das tensões
na malha (note que há apenas uma!), temos:
vx
4 2k
v x 0 v x vca 8V
4000
8
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Resistência do circuito desativado, entre A e
B:
3k
2 k
A
vx
4000
vx
B
RTh ?
Note que não conseguimos calcular a
resistência entre A e B devido à presença do
gerador de corrente.
Porém, podemos determinar essa resistência
indiretamente, por meio da relação entre os
equivalentes de Thévenin e de Norton:
vca
icc
R
R
R
vca
icc
9
EA513 – Circuitos Elétricos – DECOM – FEEC – UNICAMP – Aula 5
Portanto, precisamos determinar icc .
2 k
4V
3k
vx
0
4000
2 k
3k
4V
vx 0
icc
4
A
5000
0,8mA
icc
Finalmente, R
8V
10 k
8
10k , e
3
0,8 10
0,8mA
10 k
10












