exerc_exame - Moodle @ FCT-UNL

1. Uma pequena bola, é lançada verticalmente para cima, com uma determinada velocidade
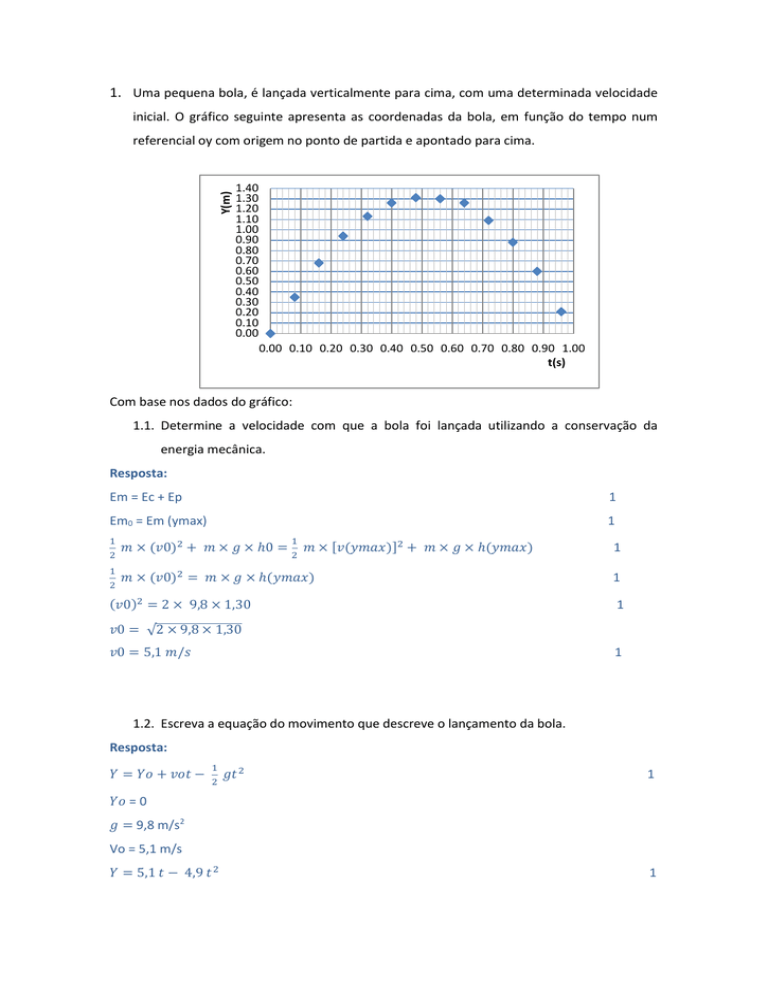
inicial. O gráfico seguinte apresenta as coordenadas da bola, em função do tempo num
Y(m)
referencial oy com origem no ponto de partida e apontado para cima.
1.40
1.30
1.20
1.10
1.00
0.90
0.80
0.70
0.60
0.50
0.40
0.30
0.20
0.10
0.00
0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00
t(s)
Com base nos dados do gráfico:
1.1. Determine a velocidade com que a bola foi lançada utilizando a conservação da
energia mecânica.
Resposta:
Em = Ec + Ep
1
Em0 = Em (ymax)
1
1
2
𝑚 × (𝑣0)2 + 𝑚 × 𝑔 × ℎ0 =
1
2
1
2
𝑚 × (𝑣0)2 = 𝑚 × 𝑔 × ℎ(𝑦𝑚𝑎𝑥)
𝑚 × [𝑣(𝑦𝑚𝑎𝑥)]2 + 𝑚 × 𝑔 × ℎ(𝑦𝑚𝑎𝑥)
(𝑣0)2 = 2 × 9,8 × 1,30
1
1
1
𝑣0 = √2 × 9,8 × 1,30
𝑣0 = 5,1 𝑚/𝑠
1
1.2. Escreva a equação do movimento que descreve o lançamento da bola.
Resposta:
𝑌 = 𝑌𝑜 + 𝑣𝑜𝑡 −
1
2
𝑔𝑡 2
1
𝑌𝑜 = 0
𝑔 = 9,8 m/s2
Vo = 5,1 m/s
𝑌 = 5,1 𝑡 − 4,9 𝑡 2
1
1.3. Determine a velocidade da bola nos instantes t = 0,08 s e t = 0,94 s.
Resposta:
𝑣 = 𝑣𝑜 + 𝑔𝑡.
𝑣 = 5,1 − 4,9 𝑡.
1
Para t = 0,08 s
𝑣 = 5,1 − 4,9 × 0,08
𝑣 = 4,71 𝑚/𝑠
1
Para t = 0,94 s
𝑣 = 5,1 − 4,9 × 0,94
𝑣 = 0,494 𝑚/𝑠
1
1.4. Explique o que acontece a velocidade e á aceleração durante a subida e durante a
descida.
Resposta:
Durante a subida a velocidade diminui até que a bola pára no ponto de altura máxima,
invertendo o sentido do movimento.
1
Durante a descida a velocidade inicial é zero e aumenta até atingir, á chegada à superfície, a
mesma velocidade com que foi lançada.
1
A aceleração mantêm-se constante durante a subida e a descida sendo o seu valor igual à
aceleração da gravidade (g = 9,8 m/s) com sinal negativo uma vez que se está a considerar o
eixo do Y o sentido positivo.
1
1.5. Determine dois instantes de tempo em que a bola tenha a mesma velocidade.
Resposta:
A bola tem a mesma velocidade quando se encontra á mesma distância da origem do
referencial durante a subida e durante a descida.
1
Consideremos Y = 0,68 m
𝑌 = 5,1 𝑡 − 4,9 𝑡 2
0,68 = 5,1 𝑡 − 4,9 𝑡 2
0 = −0.68 + 5,1 𝑡 − 4,9 𝑡 2
Fazendo a formula resolvente dá t = 0,16 s e t = 0,88 s
1
1.6. Determine a força de impacto com que a bola atinge a superfície, considerando que
tem uma massa de 0,25 Kg.
Resposta:
Segundo a 2º lei de Newton 𝐹 = 𝑚 × 𝑎
Neste caso 𝑎 = 𝑔 = 9,8 𝑚/𝑠 2
Logo 𝐹 = 𝑃
𝑃 = 0,25 × (−9,8)
𝑃 = −2,45 𝑁
A força de impacto tem o valor de 2,45 N . É uma força contrária ao movimento .