Leis de Newton Aplicadas num Autorama com “loop”

Leis de Newton Aplicadas num Autorama com “loop”
Gabriela Matos, Cláudio de Conti, Campus Experimental de Itapeva, Engenharia Industrial
Madeireira, [email protected], BAAE II
Palavras Chave: Leis de Newton, Autorama, loop.
Introdução
O presente trabalho é parte do projeto de extensão
universitária intitulado "Ensinando Física e
Matemática com um Autorama", com o apoio da
PROEX e que está sendo realizado no Campus de
Itapeva. Neste trabalho propõe-se uma atividade
experimental para medir a mínima velocidade que
um carrinho de autorama necessita para realizar um
“loop” e não cair. A velocidade medida será
comparada com o cálculo teórico desta velocidade,
obtida com as Leis de Newton (LN). Com base
nesta
atividade
pretende-se
propor
uma
aprendizagem significativa dos conceitos físicos
envolvidos nesta prática experimental.
Material e Métodos
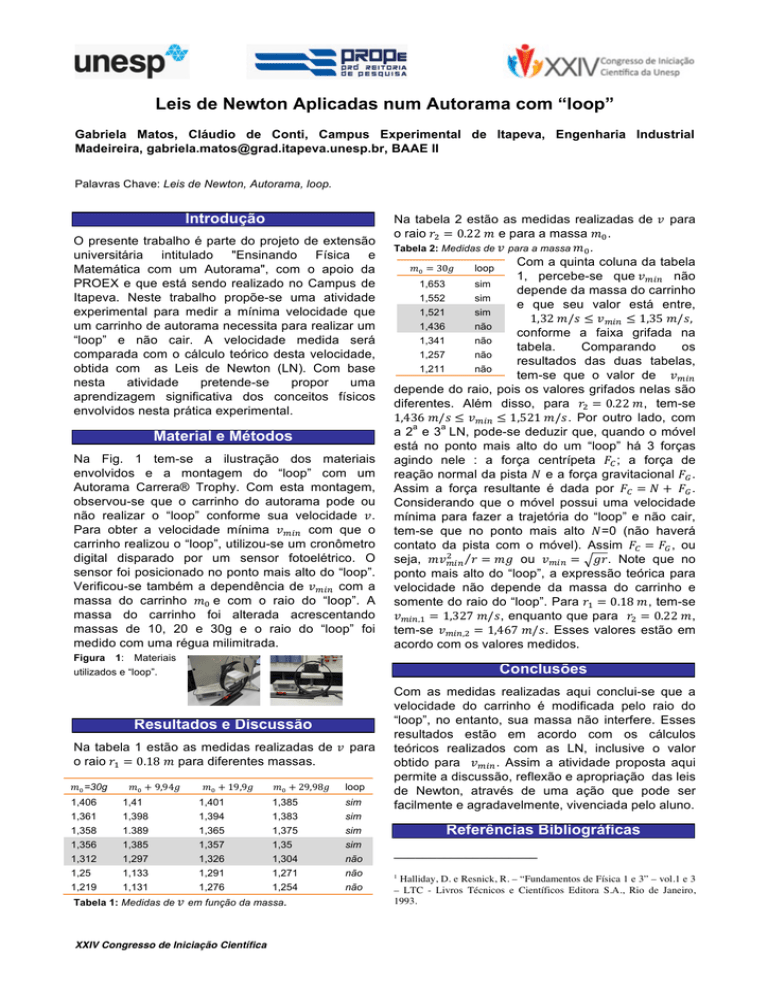
Na Fig. 1 tem-se a ilustração dos materiais
envolvidos e a montagem do “loop” com um
Autorama Carrera® Trophy. Com esta montagem,
observou-se que o carrinho do autorama pode ou
não realizar o “loop” conforme sua velocidade 𝑣.
Para obter a velocidade mínima 𝑣!"# com que o
carrinho realizou o “loop”, utilizou-se um cronômetro
digital disparado por um sensor fotoelétrico. O
sensor foi posicionado no ponto mais alto do “loop”.
Verificou-se também a dependência de 𝑣!"# com a
massa do carrinho 𝑚! e com o raio do “loop”. A
massa do carrinho foi alterada acrescentando
massas de 10, 20 e 30g e o raio do “loop” foi
medido com uma régua milimitrada.
Figura
Na tabela 2 estão as medidas realizadas de 𝑣 para
o raio 𝑟! = 0.22 𝑚 e para a massa 𝑚! .
Tabela 2: Medidas de 𝑣 para a massa 𝑚! .
Com a quinta coluna da tabela
𝑚! = 30𝑔
loop
1, percebe-se que 𝑣!"! não
1,653
sim
depende da massa do carrinho
1,552
sim
e que seu valor está entre,
1,521
sim
1,32 𝑚/𝑠 ≤ 𝑣!"# ≤ 1,35 𝑚/𝑠, 1,436
não
conforme a faixa grifada na
1,341
não
tabela.
Comparando
os
1,257
não
resultados das duas tabelas,
1,211
não
tem-se que o valor de 𝑣!"#
depende do raio, pois os valores grifados nelas são
diferentes. Além disso, para 𝑟! = 0.22 𝑚, tem-se
1,436 𝑚/𝑠 ≤ 𝑣!"# ≤ 1,521 𝑚/𝑠. Por outro lado, com
a
a
a 2 e 3 LN, pode-se deduzir que, quando o móvel
está no ponto mais alto do um “loop” há 3 forças
agindo nele : a força centrípeta 𝐹! ; a força de
reação normal da pista 𝑁 e a força gravitacional 𝐹! .
Assim a força resultante é dada por 𝐹! = 𝑁 + 𝐹! .
Considerando que o móvel possui uma velocidade
mínima para fazer a trajetória do “loop” e não cair,
tem-se que no ponto mais alto 𝑁=0 (não haverá
contato da pista com o móvel). Assim 𝐹! = 𝐹! , ou
!
seja, 𝑚𝑣!"#
𝑟 = 𝑚𝑔 ou 𝑣!"# = 𝑔𝑟. Note que no
ponto mais alto do “loop”, a expressão teórica para
velocidade não depende da massa do carrinho e
somente do raio do “loop”. Para 𝑟! = 0.18 𝑚, tem-se
𝑣!"#,! = 1,327 𝑚/𝑠, enquanto que para 𝑟! = 0.22 𝑚,
tem-se 𝑣!"#,! = 1,467 𝑚/𝑠. Esses valores estão em
acordo com os valores medidos.
1: Materiais
Conclusões
utilizados e “loop”.
Resultados e Discussão
Na tabela 1 estão as medidas realizadas de 𝑣 para
o raio 𝑟! = 0.18 𝑚 para diferentes massas.
𝑚! =30g
𝑚! + 29,98𝑔
loop
1,406
1,41
𝑚! + 9,94𝑔
1,401
𝑚! + 19,9𝑔
1,385
sim
1,361
1,398
1,394
1,383
sim
1,358
1.389
1,365
1,375
sim
1,356
1,385
1,357
1,35
sim
1,312
1,297
1,326
1,304
não
1,25
1,133
1,291
1,271
não
1,219
1,131
1,276
1,254
não
Tabela 1: Medidas de 𝑣 em função da massa.
XXIV Congresso de Iniciação Científica
Com as medidas realizadas aqui conclui-se que a
velocidade do carrinho é modificada pelo raio do
“loop”, no entanto, sua massa não interfere. Esses
resultados estão em acordo com os cálculos
teóricos realizados com as LN, inclusive o valor
obtido para 𝑣!"# . Assim a atividade proposta aqui
permite a discussão, reflexão e apropriação das leis
de Newton, através de uma ação que pode ser
facilmente e agradavelmente, vivenciada pelo aluno.
Referências Bibliográficas
____________________
1
Halliday, D. e Resnick, R. – “Fundamentos de Física 1 e 3” – vol.1 e 3
– LTC - Livros Técnicos e Científicos Editora S.A., Rio de Janeiro,
1993.