FMC_Cap7.3_slides

Capítulo VII.3
Capítulo VII.3
Magnetismo
FERROMAGNETISMO
(i) A interacção entre momentos magnéticos pode favorecer o seu alinhamento
paralelo, em átomos vizinhos
Como se todos “sentissem” o mesmo campo.


Weiss propôs que este campo molecular (ou campo de Weiss) fosse: Bm   M
 é o “responsável” pelo alinhamento dos spins
 “mede
mede o efeito
efeito” do alinhamento (ordenação) dos mesmos spins
 o modelo de Weiss é fenomenológico
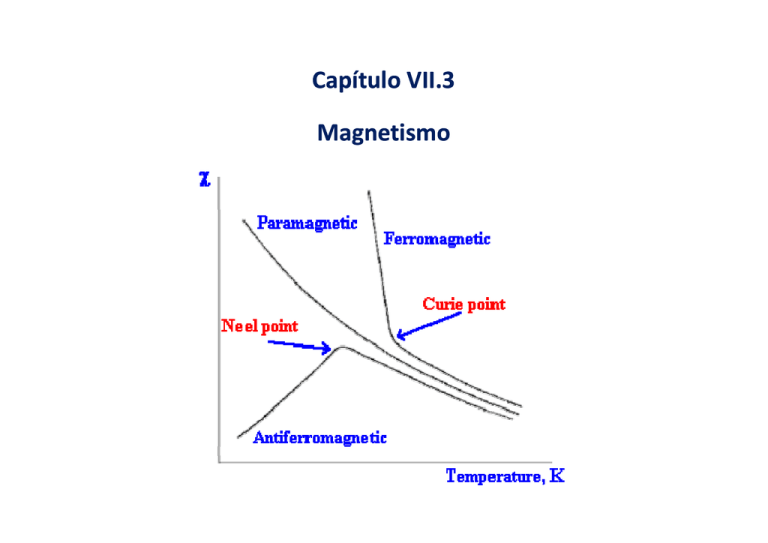
(ii) Para cada ferromagnete existe uma temperatura de transição  temperatura
de Curie (TC)
(iii) A altas temperaturas, a agitação térmica (contraria o alinhamento e ) conduz a
uma susceptibilidade semelhante à de um paramagnete  Lei de Curie‐Weiss
1

(    para T  TC )
T  TC
(iv) A T<TC domina a interacção magnética e surge uma magnetização
espontânea
ANTIFERROMAGNETISMO
Se a interacção de troca for negativa,
negativa J<0,
J<0 os momentos magnéticos vizinhos
orientam‐se antiparalelamente
Modelo proposto por Néel  Duas subredes que se interpenetram:
 Magnetismo fraco:  pequeno  Para T>
T>TTN  >0
>0, com máximo a T=TN  temperatura de Néel
 Para T<
T<TTN   diminui (agitação térmica)
DOMÍNIOS FERROMAGNÉTICOS
E muitos
Em
it sólidos
ólid ferromagnéticos
f
éti
observa‐se:
b
1. M0 a T<TC na ausência de campo aplicado
2 Aplicando um campo fraco B10‐6 T atinge
2.
atinge‐se
se a magnetização de saturação (Ms)
Porquê?
Weiss propôs (i) Num ferromagnete existem domínios magnéticos. A direcção da
magnetização varia de domínio para domínio, podendo o resultado
global ser M0
(ii) Os domínios estão separados por paredes (de Bloch)
Porque se formam os domínios?
Em cada sólido, a configuração dos domínios (número e dimensões) é o resultado
da competição de várias contribuições para a energia de um sólido magnético
1 Energia
1.
Energia de troca de troca  mínima quando todos os spins mínima quando todos os spins 
favorece um só domínio
2 Energia magnetostática 2. Energia magnetostática E
i
á i  máxima quando nas condições 1.
á i
d
di õ 1
favorece maior número de domínios
EE0
EE0/2 /2  EE0/N /N
domínios de clausura: E0
Os domínios magnéticos O
d í i
éti
podem observar‐se
3. Energia associada às paredes de Bloch
3
e g a assoc ada às pa edes de oc
“Parede”  alguns planos atómicos, ao longo dos quais a magnetização roda 180o
 C
Custo energético para manter um par de spins éi
d
i
desalinhados () JS22
 Ao longo de N planos a rotação é g
p
ç
//N (cada spin)
(
p )
2

2
 Custo energético: JS
N2
tende para zero se N  muitos domínios
4. Anisotropia magnetocristalina
4. Anisotropia magnetocristalina
A rotação dos spins altera a energia de troca e a energia electrostática da
distribuição de carga em pares de átomos – limita a largura das paredes
CICLO DE HISTERESE
A
Explicação em termos de domínios:
A  a magnetização tem o seu
valor máximo: magnetização de
saturação
Mr  magnetização remanescente
Hc  campo coercivo
i
MATERIAIS MAGNÉTICOS MOLES E DUROS
Materiais magnéticos duros
Materiais magnéticos moles
 bons magnetes permanentes: Mr,
Hc elevados
 transformadores (Ms elevado)
 muitas fronteiras de grão e
imperfeições
 grão pequeno ( 10 nm)
 pretende‐se
inverter,
com
frequência elevada, o sentido da
magnetização
 a magnetização tem de seguir o
campo rapidamente
PARAMAGNETISMO DE PAULI
 MAGNETISMO EM METAIS MAGNETISMO EM METAIS  ELECTRÕES LIVRES
ELECTRÕES LIVRES
Cada estado k de um metal pode ser ocupado por dois electrões 
Quando se aplica um campo magnético a energia de cada electrão aumenta ou
diminui conforme a orientação do seu spin  para do gás de electrões = Pauli
1
n  n  g ( E F )  B B
2
M   B n  n   g ( E F )  B2 B
 Pauli 
0  B2
O paramagnetismo de Pauli é um efeito muito pequeno O
ti
d P li é
f it
it
 só contribuem electrões com EEF
3n
2 EF
independente de T
d
d
d
DIFRACÇÃO DE NEUTRÕES
A estrutura magnética de Mn O:
 os iões Mn formam uma rede
cúbica de faces centradas
 os iões de
representados
Difractograma de neutrões de Mn
de Mn O, abaixo e e acima
acima da temperatura TN
O
não
estão