Última Aula
6872 - Fundamentos de
Eletrônica
Revisão Matemática
Elvio J. Leonardo
Grandezas Elétricas
Componentes Elétricos
Universidade Estadual de Maringá
Departamento de Informática
Instrumentos de Medição
Bacharelado em Ciência da Computação
2014
2
Roteiro
Lei de Ohm
Relação entre tensão e corrente
Associação de Resistores
Paralelo
Lei de Ohm
Para um condutor em condições de estabilidade
(temperatura constante, sem influência de campos
eletromagnéticos espúrios, etc.), a corrente entre
dois pontos é proporcional a tensão aplicada
A constante de proporcionalidade é a resistência
elétrica
Série
Lei de Ohm especifica a relação
Análise de Circuitos
Tensão/Corrente em um resistor
Matematicamente
Leis de Kirchhoff
Lei da Malhas
Lei dos Nós
3
4
Lei de Ohm
Exemplos:
Exemplos:
Qual é a corrente que atravessa uma resistência de 20 Ω
conectada a uma pilha de 1,5 V?
– ,
0,075 75 mA
Uma resistência de 1000 Ω = 1 kΩ
Ω é atravessada por uma
corrente de 3 mA. Qual é a tensão sobre a resistência?
– 1000 0,003 3 V
Uma lâmpada ligada em 127 V consome 0,145 A = 145 mA.
Qual o valor da sua resistência?
– Lei de Ohm
,
Uma lâmpada está marcada como 127 V e 100 W. Qual é a
sua resistência?
– 0,787 787 mA, – 3,33 A, Associação em Série
,
161Ω
,
3,6Ω
Portanto
మ
5
Associação de Resistores
Uma lâmpada automotiva está marcada como 40 W. Qual é
a sua resistência?
– 876Ω
6
Associação de Resistores
Associação em Série
Resistores estão em série quando a mesma corrente passa
por eles em sequência
Corrente que circula pelos resistores é a mesma
Equivalência hidráulica:
Circuito Equivalente
– canos colocados um após o outro (podem ter diâmetros e
comprimentos diferentes)
– o fluxo de água que passa pelos canos é o mesmo
– a pressão da água em cada um deles é diferente
Tensão sobre os resistores é diferente
– , , ..., – ⋯ – ⋯ – ⋯ Conclusão: Resistência equivalente é
a soma das resistências individuais
– , 1,2, … , Tensão total é dividida entre os resistores
7
8
Associação de Resistores
Associação de Resistores
Associação em Paralelo
Associação em Paralelo
Resistores estão em paralelo quando eles estão conectados
ao mesmo potencial elétrico
Tensão sobre os resistores é a mesma
Equivalência hidráulica:
Circuito Equivalente
Corrente pelos resistores é diferente
– canos colocados um ao lado do outro (podem ter diâmetros e
comprimentos diferentes)
– – a pressão da água é igual em todos os canos
– ⋯ – o fluxo de água que passa pelos canos é diferente
– –
,
భ భ
భ
మ
,
మ
..., ⋯
మ
⋯
9
Associação em Paralelo
– , 1,2, … , Corrente total é dividida entre os resistores
Outra conclusão: A condutância equivalente é a soma das
condutâncias individuais
– ⋯ Resultados especiais
భ మ
భ మ
11
Associação de Resistores
Combinação Série-Paralelo
Conclusão: O inverso da resistência equivalente é a soma
dos inversos das resistências individuais
– Para resistores iguais: 10
Associação de Resistores
– Para 2 resistores:
Circuitos mais complexos são, em geral, combinação de
associações em série e em paralelo
A análise deve
dividir o circuito
em partes onde
apenas uma das
associações (série
ou paralela) possa
ser identificada e
resolvida
12
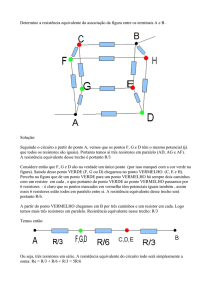
Associação de Resistores
Exemplos
Exemplos
Determine a resistência equivalente entre os pontos A e B
– భ 2 3 5 10Ω
– మ Associação de Resistores
5Ω
Determine a resistência
equivalente entre os
pontos A e B
×
15Ω
– భ – 6 5 4 15Ω
– మ – య – ర భ భ భ
భబ భబ ఱ
భ భ
భఱ లబ
2,5Ω
12Ω
10Ω
13
Associação de Resistores
Cont...
– , 2,5 15 17,5Ω
– 2,5 20,5 10 30 63Ω
– 40 12 52Ω
Análise de Circuitos
Nó: ponto do circuito em que três ou mais
terminais estão ligados, podendo ser terminais de
quaisquer elementos do circuito
Exemplos
– , 14
Exemplo: Nó B
Ramo: é a ligação entre nós consecutivos, sendo
que ao longo do ramo, a corrente elétrica é a mesma
31,5Ω
Exemplos: Ramos AB e EF
– 17,5 31,5 52 101Ω
15
Malha: caminho fechado cujos lados são formados
por ramos
16
Análise de Circuitos
No circuito ao lado
Leis de Kirchhoff
Lei das Correntes (ou Nós)
São nós os pontos e Lei das Tensões (ou Malhas)
São ramos:
Em homenagem ao físico alemão Gustav Kirchhoff
– o quatro caminhos entre os pontos e São malhas:
– o percurso formado pela fonte de tensão de 10 V e resistências de 5
Ωe2Ω
– o percurso formado pelas resistências de 2 Ω e 3 Ω
– o percurso formado pela resistência de 3 Ω e fonte de corrente 2 A
– outras combinações...
São baseadas no princípio da conservação da carga
elétrica
São usadas para na resolução de circuitos, isto é,
para determinas as tensões e correntes de um
determinado circuito
Com nós, obtém-se ! "# equações linearmente
independentes
Com $ ramos, obtém-se $ ! "# equações linearmente
independentes
17
18
Leis de Kirchhoff
Lei das Correntes
Leis de Kirchhoff
Lei das Tensões
A soma algébrica das correntes em um nó deve ser nula
A soma algébrica das tensões ao longo de uma malha deve
ser nula
Exemplos:
Exemplos:
– Nó A: ! ! 0
– Malha 1: ! ! 0
– Nó B: ! 0
– Malha 2: ! ! 0
– Malha 3: ! 0
– Observe que apenas 1 destas equações é linearmente
independentes
– Ou seja, % 2 nós produzem N ! 1 1 equação linearmente
independente
19
– Observe que apenas 2 destas equações são linearmente
independentes
– Ou seja, 3 ramos e % 2 nós produzem ! % 1 2
equações linearmente independentes
20
Leis de Kirchhoff
Aplicação das Leis de Kirchhoff para resolver o
circuito
Exemplos
Hetem pg. 9
Passo 1: Leis de Kirchhoff
Identificar nós, ramos e malhas
1) ! ! 0
Escolher e identificar as correntes
2) ! ! 0
Assinalar a polaridade das quedas de tensão
3) ! ! 0
– se elemento passivo, a corrente entra no polo de maior potencial
– se elemento ativo, a corrente entra no polo de menor potencial
Passo 2: Lei de Ohm
1) 100 100 12
Obter as equações de nós e malhas
2) 100 ! 50 ! 50 0
Resolver o sistema de equações lineares
3) ! ! 0
Passo 3: Resolução do sistema de equações lineares
– 0,08 80 mA, 0,04 40 mA, 0,04 40 mA
– 8 V, 4 V, 2 V, 2 V
21
22
Exemplos
Hetem pg. 9, com Resistência Equivalente
1) 50 50 100 100 150Ω
3) ! ! 0
0,08 80 mA
4) ! ! 0
2) 0,08×100 8 V
5) ! 0
3) 0,08×50 4 V
4) 5) 1) ! ! 0
2) ! ! 0
Correntes e Tensões
Hetem pg. 11
Passo 1
Resistência Equivalente
1) Exemplos
Passo 2
0,04 40 mA
0,04 40 mA
1) 200 50 20
4) ! ! 0
2) 50 ! 120 ! 50
0
5) ! 0
3) 50
150 5
6) 0,04×50 2 V
7) 0,04×50 2 V
23
24
Exemplos
Hetem pg. 11 (cont.)
Exemplos
Hetem pg. 11, com Superposição
Passo 3
Apenas (
– 0,0828 82,8 mA
1) 200 ! 50 20
4) ! ! 0
– 0,0689 68,9 mA
2) 50 ! 120 ! 50
0
5) ! 0
– 0,0139 13,9 mA
3) 50
150 0
Solução para (
– 0,0354 35,4 mA
– 0,0215 21,5 mA
– 0,0841 84,1 mA
– 16,6 V
– 0,0638 63,8 mA
– 3,44 V
– 0,0203 20,3 mA
– 1,67 V
– 0,0152 15,2 mA
– 1,77 V
– !0,0051 !5,1 mA
– 2,23 V
25
26
Exemplos
Hetem pg. 11, com Superposição (c0nt.)
Exemplos
Hetem pg. 16
Todos os resistores em paralelo
Apenas (
1) 200 ! 50 0
4) ! ! 0
2) 50 ! 120 ! 50
0
5) ! 0
3) 50
150 5
Solução completa
Solução para (
– !0,0013 !1,3 mA
– 84,1 ! 1,3 82,8 mA
– 0,0051 5,1 mA
– 63,8 5,1 68,9 mA
– !0,0063 !6,3 mA
– 20,3 ! 6,3 14,0 mA
– 0,0203 20,3 mA
– 15,2 20,3 35,5 mA
– 0,0266 26,6 mA
– !5,1 26,6 21,5 mA
27
5A
2,5 A
1,67 A
1,25 A
1) 2)
3)
4)
5) 100 V
28
Exemplos
Hetem pg. 16
Exemplos
Hetem pg. 16
Todos os resistores em série
Passo 1
1) 200 120 10 180 ! 20 0, ou seja, 0,02 20 mA
1) ! ! 0
2) 0,02×200 4 V
2) ! 0
3) 0,02×120 2,4 V
3) ! ! 0
Passo 2
4) 0,02×180 3,6 V
1) 200 100 20
2) 100 ! 120 150 5
3) ! I ! I 0
Passo 3
– 68,3 mA, 63,4 mA, 5,0 mA
– 13,7 V, 6,3 V, 0,6 V, 0,8 V
29
Exemplos
Hetem pg. 17
30
Circuito Equivalente de Thévenin
Qualquer circuito linear pode ser substituído nos
terminas A e B por um circuito equivalente
composto de fonte de tensão e resistência
Passo 1
1) ! ! ! 0
A tensão equivalente * é a tensão entre os terminais A e B
em circuito aberto
2) ! 0
3) ! ! 0
Passo 2
1) 200 120# 200 20
2) 200 ! 120 10
A resistência equivalente $ é aquela obtida a partir dos
terminas A e B
– Para deve-se substituir fontes de tensão por curto-circuitos e
fontes de correntes por circuitos abertos
3) ! I ! I 0
Passo 3
– 34,8 mA, 44,3 mA, !9,5 mA
– 7,0 V, 4,2 V, 8,9 V, !1,1 V
31
32
Circuito Equivalente de Norton
Qualquer circuito linear pode ser substituído nos
terminas A e B por um circuito equivalente
composto de fonte de corrente e resistência
Circuitos Equivalentes
Circuitos equivalentes de Thévenin e Norton são
usados em análise e simplificação de circuitos
A corrente equivalente + é a corrente entre os terminais A
e B em curto-circuito
Desenvolvidos pelo cientista alemão Hermann von
Helmholtz e pelo engenheiro francês Léon
Thévenin
A resistência equivalente $ é aquela obtida a partir dos
terminas A e B
Equivalências:
– Para deve-se substituir fontes de tensão por curto-circuitos e
fontes de correntes por circuitos abertos
$ $
* $ +
+ ࢚ࢎ
࢚ࢎ
33
34
Exemplos
Calcular os circuitos equivalentes [Hetem, pg. 13]
భ మ – ∥ 10k
!!
భ మ
భ మ
10V
!!
!!
3,33kΩ
భ
!
– ∥ – 3mA
8k
!
!
భ మ
భ మ
2V
!
!
!
!
6,67kΩ
,!
!
300μA
Equivalência
Equivalência
మ
– 6,67kΩ
– 3,33kΩ
– భ మ – Norton
Norton
– Calcular os circuitos equivalentes [Hetem, pg. 15]
Thévenin
Thévenin
– Exemplos
– 3mA
– 3m3,33k 10V
35
,!
300μA
– 300μ×6,67k 2V
36
Exemplos
Calcular os circuitos equivalentes entre A e B
Thévenin
– Superposição
ଵଶ
– 2Ω
» (1) ௧ଵ ସ଼ାଵ 16 3V
Norton
ସ଼×ଵ
» (2) ௧ଶ ସ଼ାଵ 1 12V
– !1A
» ௧ ௧ଵ ௧ଶ 3 12 9V
– 2Ω
– 16 ∥ 48 Equivalência
Calcular os circuitos equivalentes entre a e b
Thévenin
– !1A2Ω !2V
– Exemplos
#
×
12Ω
!1A
– !1×2 !2V
37
Exemplos
Calcular os circuitos equivalentes entre a e b
Norton
– Superposição
ଵଶ
» (1) ଵ ସ଼ 250mA
» (2) ଶ 1A
» ଵ ଶ 0,25 1 750mA
– 12Ω
Equivalência
–
#$
!750mA
– !0,75×12 !9V
39
38