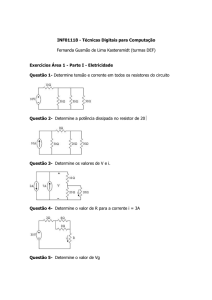
1ª LISTA DE EXERCICIOS – 1º SEMESTRE DE 2008 1) Determine

1ª LISTA DE EXERCICIOS – 1º SEMESTRE DE 2008
1) Determine a resistência equivalente entre os terminais a e b, mostrado
abaixo:
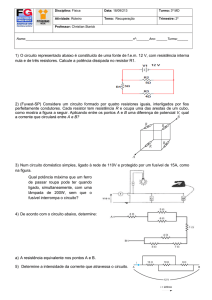
2) Calcule a capacitância equivalente da rede mostrada abaixo:
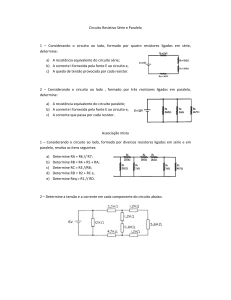
3) Determine a indutância equivalente da rede mostrada na figura abaixo:
4) As correntes ia e ib no circuito abaixo são 4A e –2A, respectivamente.
a) Determine ig.
b) Determine as potências dissipadas nos oito resistores.
c) Determine Vg.
d) Mostre que a potência fornecida pela fonte de corrente é igual à potência
recebida
por todos os outros elementos.
5) Ache o valor da corrente i e da potência dissipada no resistor de 4Ω.
6) Determine a tensão Vs do circuito mostrado abaixo:
7) Determine as tensões e as correntes nos resistores do circuito representado
abaixo.
Determine as tensões nas fontes de corrente e a corrente através da fonte de
tensão.
Determine ainda as potências dissipadas em cada resistor e fornecidas pelas
fontes.
8) A tensão entre os terminais de um capacitor de 50μF é dada por
V(t)=10cos(377t) V.Escrevas expressões para a corrente i(t) que atravessa o
capacitor(convenção dereceptor), para a energia armazenada E(t) e para a
potencia P(t) que lhe é fornecida.Obtenha ainda a potência média, definida por
P=377∫02π/377 P(t) dt.
9) Um indutor linear variável com o tempo, de indutância L=L0[1+mcos(ωt)],
éatravessado por uma corrente constante I. Qual a tensão entre seus terminais?
10) No circuito mostrado, a chave abre no tempo t=0. Determine i(t) para t>0.
11) A corrente i0 no circuito abaixo é 4A.
a) Determine i1.
b) Determine as potências dissipadas nos cinco resistores.
c) Verifique que a potência total dissipada no circuito é igual à potência
fornecida pela
fonte de 180 V.
12) Determine a corrente i(t) no circuito representado na figura abaixo. Esboce
um
gráfico para essa corrente em função do tempo. A chave passa para a posição
2 depois
de muito tempo na posição 1. Determine novamente a corrente i(t) no mesmo
circuito.
A chave passa para a posição 1 depois de muito tempo na posição 2.
13) Encontre i1, i2,e i3 para o circuito mostrado abaixo.
14) Encontre as relações de equivalência entre as resistências dos circuitos (Y
– Δ) e
(Δ - Y) abaixo: