Elasticidade e Análise Marginal

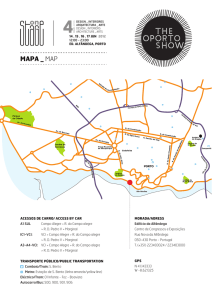
GOVERNO FEDERAL
MINISTÉRIO DA EDUCAÇÃO
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO
CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA
PROF. PEDRO MACÁRIO DE MOURA
MATEMÁTICA APLICADA A ADM – 2015.2
Discentes __________________________________________CPF
1º Período Turma A1 – Sala NT 03 Lista de Aplicações das Derivadas
Data: 29/01/2016
Elasticidade e Análise Marginal
Funções Marginais – Em Economia e Administração, dada uma função
costuma-se
utilizar o conceito de função marginal para avaliar o efeito causado em
por uma pequena variação de .
Custo Marginal
Em Economia a variação de uma quantidade em relação à outra pode ser descoberta
por qualquer dos dois conceitos: o de Média ou o de Marginal. O conceito de média,
expressa a variação de uma quantidade sobre um conjunto específico de valores de uma
segunda quantidade, enquanto que o conceito de marginal é a mudança instantânea na
primeira quantidade que resulta de uma mudança em unidades muito pequenas na segunda
quantidade.
Suponha que
A função
seja o custo total de produção de q unidades de um certo produto.
é chamada de função custo total (como já vimos anteriormente). Em
circunstâncias normais
unidades de um produto,
e
são positivas. Note que, como q representa o número de
tem que ser inteiro não negativo, de modo que tenhamos as
condições de continuidade para a função .
O custo médio da produção de cada unidade do produto é obtido dividindo-se o custo
total pelo número de unidades produzidas; isto é,
, onde
é chamada função
custo médio.
Suponhamos que o número de unidades de uma determinada produção seja
ela tenha sido alterada por . Então a variação no custo total é dada por
, e que
e
a variação média no custo total em relação à variação no número de unidades produzidas é
dada por:
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 1
Os economistas usam o termo Custo Marginal para limite do quociente (1) quando
tende a zero, desde que o limite exista. Esse limite é a derivada de
em
; portanto a
definição de custo marginal será:
Se
é o custo de produção de
Marginal, quando
, é dada por
unidades de um certo produto, então o Custo
, caso exista o limite. A função
é chamada
Função Custo Marginal e frequentemente é uma boa aproximação do custo de produção de
uma unidade adicional.
Na definição acima,
total quando
pode ser interpretada como a taxa de variação do custo
unidades são produzidas.
Temos também as funções marginais para recita e lucro
Receita marginal (
) – Variação na receita total decorrente da venda de uma unidade na
quantidade vendida do bem. Já vimos que
preço e
Lucro marginal (
Elasticidade-Preço
, onde
éa
é a quantidade.
) – Variação do lucro total.
–
– Mede a variação percentual da quantidade ofertada decorrente de
uma variação percentual no preço,
são números reais,
é o preço e
, onde
e
a função de demanda.
Inelástica;
Elástica;
Elasticidade unitária.
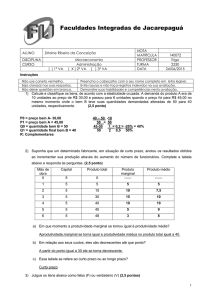
Exemplo 01
Suponha que o custo total ao se fabricar q un. de brinquedos seja de C (q)  3q 2  5q  10 .
a) Deduza a fórmula do custo marginal.
Resp.: C’(q) = 6q + 5
b) Qual é o custo marginal de 50 unidades produzidas?
Resp.: C’(50) = 305
c) Qual é o custo real de produção do 51º brinquedo?
Resp.: C(51)=308
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 2
Note que as respostas dos itens b) e c) diferem por R$ 3,00, isto é, o custo marginal é
próximo do custo real de produção de uma unidade adicional. Esta discrepância ocorre porque
o custo marginal é a taxa de variação instantânea de
variação em . Logo,
é o custo aproximado da produção do 51º brinquedo.
Observe que o cálculo de
–
em relação a uma unidade de
no exemplo, é mais simples do que o de
.
Os economistas frequentemente aproximam o custo da produção de uma quantidade
adicional usando a função custo marginal. Mais claramente,
enésima unidade que as
é o custo aproximado da
primeiras unidades tiverem sido produzidas.
As respostas dos itens b e c do exemplo anterior são muito próximas por causa da
proximidade dos pontos (50; C(50)) e (51; C(51)), e porque esses pontos pertencem a uma
porção praticamente linear da curva de custo. Para tais pontos, o coeficiente angular da
secante é uma boa aproximação do coeficiente angular da tangente. Como usualmente se
obtém esta aproximação e sendo mais fácil, de maneira geral, calcula-se o custo marginal
como aproximação do custo real de produção de uma unidade adicional.
De maneira geral, em Economia, Análise Marginal se refere ao uso de derivadas de
funções para estimar a variação ocorrida no valor da variável dependente, quando há um
acréscimo de 1 unidade no valor da variável independente.
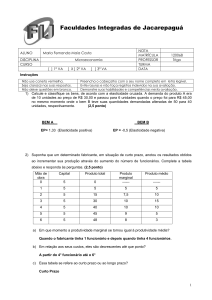
Exemplo 02
Suponha que o custo total de produção de q unidades de canetas seja de C (q)  2q 2  q  8.
Ache as funções:
a) Custo Médio
Resp.:
b) Custo Marginal
Resp.: C’(q) = 4q + 1
C (q)
8
 2q  1 
q
q
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 3
Exercícios Funções Marginais e Elasticidade
–
01. Dada à função custo anual de uma empresa
. Ache o custo
médio.
02. Dada à função receita
, obtenha a
em
–
03. Dada à função custo
. Resp. 800.
obtenha:
a) O custo marginal Cmg; Resposta: C’(x) = 0,3x2 – 36x + 1500;
b) Cmg (65) e a interpretação do resultado; Resposta C’(65) = 427,5;
c) Cmg (150) e a interpretação do resultado. Resposta C’(150) = 2850.
04. Uma commodity tem sua função da demanda modelada por
função custo total modelado por é
05. Suponha que
e sua
. Qual é o lucro médio por unidade?
seja a receita total recebida da venda de
mesas.
Determine a receita marginal quando 50 mesas são vendidas. Qual a receita efetiva da venda
da 51a mesa?
06. Seja
, a função receita diária, para a fabricação de fogões, onde
é o número de unidades produzidas diariamente. Atualmente, o fabricante está produzindo
400 fogões por dia e pretende elevar este número para 401.
a) Use análise marginal para estimar o ganho adicional produzido pelo 401° fogão.
b) Qual a diferença entre o ganho real e o aproximado calculado no item (a).
07. A quantidade
demanda
e o preço
de certo produto estão relacionados pela seguinte equação de
.
a) Determine a elasticidade de demanda em função do preço
b) Calcular a elasticidade de demanda para
c) Calcular a elasticidade de demanda para
08. A função receita marginal de um produtor monopolista é
. Determine a
função receita total e deduza a equação de demanda corespondente.
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 4
09. Sendo
demandada e
a função demanda de um bem, onde
é a quantidade
o preço. Determinar:
a) A função receita marginal;
b) A receita marginal para 13.863 unidades.
10. A quantidade
e o preço
de certo produto estão relacionados pela seguinte equação de
–
demanda
. Determine a elasticidade de demanda em função do
preço, quando
11. Suponha que o custo total semanal em real incorrido pela Companhia PTA para fabricação
de
–
refrigeradores seja dado pela função custo total.
Se
a) Qual o custo total envolvido na fabricação do 351º refrigerador?
b) Determine a taxa de variação da função custo total com relação a
quando
.
c) Compare os resultados obtidos nas partes (a) e (b) e faça uma análise econômica
d) O que representa
(este intervalo fechado)?
12. Uma subsidiária da Companhia Eletrônica Elektra fabrica uma calculadora de bolso
programável. A gerência determinou que o custo total diário em real para produzir essas
–
calculadoras é dado por
onde
é igual ao
número de calculadoras produzidas.
a) Determine a função custo marginal.
b) Qual é o custo marginal quando
e
13. O custo total em reais para produzir
?
unidades de um certo bem é modelado pela função
a) Determine a função custo médio.
b) Determine a função custo médio marginal.
14.
O custo de fabricação de x unidades de um produto é
.
Atualmente o nível de produção é de 25 unidades. Calcule, aproximadamente, usando
diferencial de função
, quanto varia o custo se forem produzidas 26 unidades.
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 5
15. A função receita de uma empresa é
, em que x é o número de
unidades produzidas. Atualmente o nível de produção é de 6 unidades, e a empresa pretende
reduzir a produção em 0,5 unidades. Usando a diferencial de função
, dê
aproximadamente a variação da receita. E interprete os resultados.
.
16. Em uma fábrica de ventiladores, o preço de um tipo de ventilador é dado por
onde 0  x  400. Suponha que o custo para a produção dos ventiladores
seja dado por
. Obtenha a função lucro marginal.
17. A empresa MACAMBIRA produz um determinado produto, com custo semanal dado pela
função
. Cada unidade deste produto é vendida por R$31.
Determinar a quantidade que deve ser produzida e vendida para dar o máximo lucro?
18. A função da demanda de um produto é dada por é
milhares de unidades) determine a elasticidade-preço da demanda para
(em
. Faça uma
análise da sua resposta.
19. Seja
, a função receita diária, para a fabricação de fogões, onde
é o número de unidades produzidas diariamente. Atualmente, o fabricante está produzindo
400 fogões por dia e pretende elevar este número para 401.
a) Use análise marginal para estimar o ganho adicional produzido pelo 401° fogão.
b) Qual a diferença entre o ganho real e o aproximado calculado no item (a).
20. A quantidade
e o preço
demanda
de certo produto estão relacionados pela seguinte equação de
.
a) Determine a elasticidade de demanda em função do preço
b) Calcular a elasticidade de demanda para
c) Calcular a elasticidade de demanda para
Bom Estudo!
Bibliografia
Vide PD da Disciplina
Deus não lhe dá mais do que você pode carregar. Jesus Cristo.
Página 6