Raízes primitivas e congruências de grau superior a 1

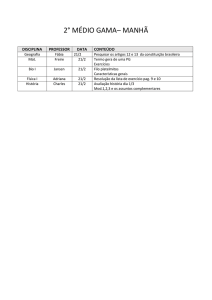
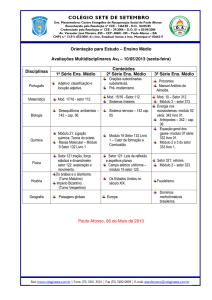
Teoria dos Números (2004/2005)
1
Raı́zes primitivas e congruências de grau superior a 1
Seja p um número primo. Sejam n ∈ N0 , a0 , a1 , . . . , an números inteiros e considere-se o
polinómio
f (x) = an xn + an−1 xn−1 + · · · + a1 x + a0 .
Suponha-se que p - ai , para algum i ∈ {0, 1, . . . , n}.
Definição. O grau da congruência f (x) ≡ 0 (mod p) é o maior i ∈ {0, 1, . . . , n} tal que
p - ai .
Por exemplo, a congruência x3 − x + 1 ≡ 0 (mod 2) tem grau 3, enquanto que a
congruência 3x4 − x2 + 2 ≡ 0 (mod 3) tem grau 2. Para m ∈ N composto define-se o grau
da congruência f (x) ≡ 0 (mod m) de modo análogo.
Das propriedades da relação de congruência módulo p resulta que, se a ∈ Z é tal
que f (a) ≡ 0 (mod p), então também qualquer outro inteiro da classe de congruência [a]p
verifica a congruência polinomial f (x) ≡ 0 (mod p). No que se segue designam-se por
soluções de uma congruência f (x) ≡ 0 (mod p) quer os inteiros que a satisfazem, quer
as classes de congruência módulo p cujos elementos satisfazem a congruência, depreendendo-se do contexto qual a situação em causa. Porém, quando se falar no número de
soluções de uma congruência polinomial f (x) ≡ 0 (mod p), estará sempre a referir-se o
número de classes de congruência módulo p cujos elementos satisfazem a congruência.
O que se pode dizer acerca do número de soluções de uma congruência polinomial
f (x) ≡ 0 (mod p)? Uma congruência destas pode não ter solução. É o que se passa, por
exemplo, com x2 − x + 1 ≡ 0 (mod 2), já que, para todo o inteiro a, a2 ≡ a (mod 2) e
portanto a2 − a + 1 ≡ 1 (mod 2) 6≡ 0 (mod 2).
O teorema seguinte, devido a Lagrange, fornece um majorante para o número de
soluções de uma congruência polinomial com grau n e cujo módulo é um primo.
Teorema. Sejam p um número primo, n ∈ N0 , a0 , a1 , . . . , an inteiros e f (x) = an xn +
an−1 xn−1 + · · · + a1 x + a0 . Se p - an (isto é, se a congruência f (x) ≡ 0 (mod p) tem grau
n) então a congruência f (x) ≡ 0 (mod p) tem no máximo n soluções.
Demonstração. A demonstração é feita por indução em n. Para n = 0, f (x) = a0 e,
por hipótese, p - a0 , logo a congruência f (x) ≡ 0 (mod p) tem zero soluções.
Seja k ∈ N0 e suponha-se que o número de soluções de qualquer congruência polinomial de módulo p e com grau inferior ou igual a k é, no máximo, igual ao grau da
congruência.
Teoria dos Números (2004/2005)
2
Prove-se que o resultado é válido para congruências de grau k + 1. Seja
f (x) = ak+1 xk+1 + ak xk + · · · + a1 x + a0 ,
onde p - ak+1 , e suponha-se que a congruência f (x) ≡ 0 (mod p) tem mais do que k + 1
soluções.
Existem u1 , u2 , . . . , uk+1 , uk+2 ∈ Z verificando f (x) ≡ 0 (mod p) e tais que ui 6≡
uj (mod p), se i, j ∈ {1, 2, . . . , k + 2} são distintos. Considere-se o polinómio
g(x) = f (x) − ak+1 (x − u1 )(x − u2 ) · · · (x − uk+1 ) .
O grau de g é inferior ou igual a k, logo g é da forma ck xk + ck−1 xk−1 + · · · + c1 x + c0 .
Suponha-se que p | ci , para todo o i = 0, 1, . . . , k. Então, para todo o a ∈ Z,
g(a) ≡ 0 (mod p) e portanto também g(uk+2 ) ≡ 0 (mod p). Mas isto significa que
f (uk+2 ) − ak+1 (uk+2 − u1 )(uk+2 − u2 ) · · · (uk+2 − uk+1 ) ≡ 0 (mod p) ,
ou seja, que
f (uk+2 ) ≡ ak+1 (uk+2 − u1 )(uk+2 − u2 ) · · · (uk+2 − uk+1 ) (mod p) .
Uma vez que f (uk+2 ) ≡ 0 (mod p) conclui-se que
p | ak+1 (uk+2 − u1 )(uk+2 − u2 ) · · · (uk+2 − uk+1 ) ,
o que é absurdo porque p é primo, p - ak+1 e p - (uk+2 − ui ), para i = 1, 2, . . . , uk+1 .
Então existe pelo menos um coeficiente no polinómio g que não é múltiplo de p e
portanto a congruência g(x) ≡ 0 (mod p) tem grau inferior ou igual a k.
Por outro lado, para i = 1, 2, . . . , k + 1, g(ui ) = f (ui ) ≡ 0 (mod p) e portanto g(x) ≡
0 (mod p) é uma congruência de grau inferior ou igual a k que tem pelo menos k + 1
soluções. Isto contradiz a hipótese de indução. A contradição resultou de se ter suposto
que a congruência f (x) ≡ 0 (mod p) tem k + 2 soluções. Assim, esta congruência tem no
máximo k + 1 soluções. A primeira variante do princı́pio de indução matemática permite
concluir que o resultado é válido para todo o n ∈ N0 .
Observação. Este resultado não é válido se o módulo da congruência não for primo.
Por exemplo, a congruência x2 + x ≡ 0 (mod 6) tem grau 2 e no entanto tem 4 soluções:
[0]6 , [2]6 , [3]6 e [5]6 .
No que se segue consideram-se congruências do tipo xn ≡ 1 (mod p), com p primo
e n ∈ N. Observe-se que uma congruência deste tipo tem sempre solução porque, pelo
3
Teoria dos Números (2004/2005)
menos, todos os inteiros da classe de congruência [1]p a verificam. Pelo Teorema de
Lagrange esta congruência tem no máximo n soluções.
Proposição. Se n | p − 1 então a congruência xn ≡ 1 (mod p) tem exactamente n
soluções, isto é, existem exactamente n classes de congruência módulo p cujos elementos
satisfazem a congruência.
Demonstração. Por hipótese existe q ∈ N tal que p − 1 = qn. Considere-se o polinómio
xp − x. Tem-se
xp − x = xqn+1 − x = x(xqn − 1) .
Uma vez que
xqn − 1 = (xn − 1) x(q−1)n + x(q−2)n + · · · + xn + 1
(exercı́cio das folhas práticas) ,
conclui-se que xp − x = (xn − 1)g(x), onde
g(x) = x x(q−1)n + x(q−2)n + · · · + xn + 1 .
Atendendo a que ap − a ≡ 0 (mod p) para todo o a ∈ Z, conclui-se que a congruência
(xn − 1)g(x) ≡ 0 (mod p) tem p soluções. Mas a congruência g(x) ≡ 0 (mod p) tem grau
(q − 1)n + 1 = qn − n + 1 = p − n logo tem no máximo p − n soluções. Então (porque
p é primo) a congruência xn − 1 ≡ 0 (mod p) tem pelo menos n soluções. Aplicando o
Teorema de Lagrange conclui-se que esta congruência tem exactamente n soluções.
Exemplo. Uma vez que 4 | (13 − 1), a congruência x4 ≡ 1 (mod 13) tem exactamente
4 soluções. Como determiná-las?
Sejam m ∈ N e a ∈ Z primo com m. Do teorema de Euler sabe-se que aϕ(m) ≡
1 (mod m) e portanto o conjunto {k ∈ N : ak ≡ 1 (mod m)} é não vazio. Assim, o
princı́pio de boa ordenação garante que este conjunto tem um mı́nimo.
Definição. Para a ∈ Z, primo com m ∈ N, chama-se ordem de a módulo m ao menor
inteiro positivo k tal que ak ≡ 1 (mod m).
Exemplo.
Sejam m = 10 e a = 9. Uma vez que 91 ≡ 9 (mod 10) e 92 ≡ 1 (mod 10), a
ordem de 9 módulo 10 é 2.
Observação. Para a primo com m, todos os inteiros da classe congruência [a]m têm
Teoria dos Números (2004/2005)
4
ordem módulo m igual à de a.
Da definição e do Teorema de Euler resulta que a ordem de a módulo m (para a
primo com m) é inferior ou igual a ϕ(m). Vai provar-se que a ordem de a módulo m
divide ϕ(m), o que será feito usando a proposição seguinte.
Proposição. Sejam m ∈ N e a ∈ Z primo com m. Seja h a ordem de a módulo m.
Então, para k ∈ N0 ,
ak ≡ 1 (mod m) ⇔ h | k .
Demonstração. Seja k ∈ N0 tal que ak ≡ 1 (mod m). Dividindo k por h obtém-se
k = qh + r com q e r inteiros, q ≥ 0 e 0 ≤ r < h. Prove-se que r = 0. Uma vez que
q
ak = ah ar , da hipótese e da definição de ordem obtém-se
ah
q
ar ≡ 1 (mod m) ⇒ 1q ar ≡ 1 (mod m) ⇒ ar ≡ 1 (mod m) .
Mas 0 ≤ r < h e h é a ordem de a módulo m, logo r tem de ser zero.
Reciprocamente suponha-se que h | k. Existe q ∈ N0 tal que k = qh e portanto
ak = ah
q
≡ 1q (mod m) ≡ 1 (mod m) .
Aplicando o Teorema de Euler obtém-se imediatamente o corolário seguinte.
Corolário.
Sejam m ∈ N e a ∈ Z primo com m. A ordem de a módulo m divide
ϕ(m).
Definição. Seja m ∈ N. Um inteiro g diz-se uma raı́z primitiva módulo m se (g, m) = 1
e a ordem de g módulo m é ϕ(m).
Exemplo.
Seja m = 10. Há exactamente 4 inteiros em {1, 2, . . . , 10} que são primos
com 10, logo ϕ(10) = 4. Uma vez que (3, 10) = 1, 31 ≡ 3 (mod 10), 32 ≡ 9 (mod 10),
33 ≡ 7 (mod 10) e 34 ≡ 1 (mod 10), conclui-se que 3 é uma raı́z primitiva módulo 10.
Dado m ∈ N, podem não existir raı́zes primitivas módulo m. Por exemplo, não
existem raı́zes primitivas módulo 8 (exercı́cio das folhas práticas). O objectivo do que se
segue é provar que, se p é primo, então existem raı́zes primitivas módulo p.
5
Teoria dos Números (2004/2005)
Proposição. Sejam m ∈ N e a e b inteiros primos com m. Se a tem ordem h módulo
m, b tem ordem k módulo m e (h, k) = 1, então ab tem ordem hk módulo m.
Demonstração. Exercı́cio das folhas práticas.
O resultado anterior é generalizável, por indução no número de factores, para um
produto de r ∈ N factores:
Lema. Sejam r, m ∈ N e a1 , a2 , . . . , ar inteiros primos com m. Para i = 1, 2, . . . , r seja
hi a ordem de ai módulo m. Se h1 , h2 , . . . , hr são primos dois a dois, então a1 a2 · · · ar
tem ordem h1 h2 · · · hr módulo m.
Proposição. Se p é primo então existem raı́zes primitivas módulo p .
Demonstração. 1 é uma raı́z primitiva módulo 2. Suponha-se que p > 2 e seja
p − 1 = q1α1 q2α2 · · · qrαr a decomposição canónica de p − 1 (q1 , q2 , . . . , qr são números
primos distintos dois a dois e α1 , α2 , . . . , αr ∈ N). Fixe-se i ∈ {1, . . . , r}. Uma vez
αi
que qiαi | p − 1, uma proposição anterior garante que a congruência xqi ≡ 1 (mod p)
αi −1
tem exactamente qiαi soluções. Analogamente a congruência xqi
≡ 1 (mod p) tem
exactamente qiαi −1 < qiαi soluções. Assim, existe ai ∈ Z que é solução da primeira
q
αi
congruência mas não é solução da segunda. Uma vez que ai i ≡ 1 (mod p), a ordem de
ai módulo p é um divisor de qiαi e portanto é da forma qik com 1 ≤ k ≤ αi . Se k ≤ αi − 1
k qiαi −1−k
α −1
αi −1−k
qi i
q
então ai
= ai i
≡ 1qi
(mod p) ≡ 1 (mod p), o que contradiz o facto de ai
αi −1
não ser solução de xqi
≡ 1 (mod p). Então k = αi , isto é, ai tem ordem qiαi módulo p.
Provou-se assim que, para i = 1, . . . , r, existe ai ∈ Z com ordem qiαi módulo p. Seja
α g = a1 a2 · · · ar . Para i, j = 1, . . . , r com i 6= j, qiαi , qj j = 1 e portanto, pelo lema
anterior, a ordem de g módulo p é
q1α1 q2α2 · · · qrαr = p − 1 = ϕ(p) ,
isto é, g é uma raı́z primitiva módulo p.
A demonstração da proposição anterior fornece um processo que pode simplificar a
procura de raı́zes primitivas módulo p, com p primo.
Exemplo. Determine-se uma raı́z primitiva módulo 13.
13 − 1 = 12 = 22 × 3. Se a1 tem ordem 4 módulo 13 e a2 tem ordem 3 módulo 13, então
6
Teoria dos Números (2004/2005)
a1 a2 é uma raı́z primitiva módulo 13. Procurem-se a1 com ordem 4 módulo 13 e a2 com
ordem 3 módulo 13. Observe-se que, em princı́pio, procurar a1 e a2 nestas condições é
mais simples do que procurar, directamente, g com ordem 12 módulo 13.
21 ≡ 2 (mod 13), 22 ≡ 4 (mod 13), 23 ≡ 8 (mod 13) e 24 = 16 ≡ 3 (mod 13), logo a
ordem de 2 módulo 13 é superior ou igual a 5.
31 ≡ 3 (mod 13), 32 ≡ 9 (mod 13) e 33 = 27 ≡ 1 (mod 13), logo 3 tem ordem 3 módulo
13. Considere-se a2 = 3.
41 ≡ 4 (mod 13), 42 ≡ 3 (mod 13), 43 ≡ −1 (mod 13) e 44 ≡ −4 (mod 13) ≡ 9 (mod 13),
logo a ordem de 4 módulo 13 é superior ou igual a 5.
51 ≡ 5 (mod 13), 52 = 25 ≡ −1 (mod 13) ≡ 12 (mod 13), 53 ≡ −5 (mod 13) ≡
8 (mod 13) e 54 ≡ 40 (mod 13) ≡ 1 (mod 13), logo 5 tem ordem 4 módulo 13. Considere-se
a1 = 5.
Assim, a1 a2 = 15 é uma raı́z primitiva módulo 13. Uma vez que 15 ≡ 2 (mod 13),
também 2 é uma raı́z primitiva módulo 13.
Proposição. Sejam m um número natural e g uma raı́z primitiva módulo m. Então
2
g, g , . . . , g ϕ(m)−1 , g ϕ(m) é um sistema reduzido de resı́duos módulo m.
Demonstração. Exercı́cio das folhas práticas.
No que se segue usam-se raı́zes primitivas para determinar as soluções (caso existam)
de congruências do tipo xn ≡ a (mod p), com p primo e a primo com p.
Proposição. Sejam p primo e a ∈ Z tal que (a, p) = 1. Considere-se a congruência
xn ≡ a (mod p) .
(1)
p−1
(i) Se a (n,p−1) 6≡ 1 (mod p) então (1) não tem soluções.
p−1
(ii) Se a (n,p−1) ≡ 1 (mod p) então (1) tem exactamente (n, p − 1) soluções.
Demonstração. Seja g uma raı́z primitiva módulo p. Uma vez que a é primo com
p e {g, g 2 , . . . , g p−1 } é um sistema reduzido do resı́duos módulo p, existe um e um só
k ∈ {1, 2, . . . , p − 1} tal que a ≡ g k (mod p). Assim,
xn ≡ a (mod p) ⇔ xn ≡ g k (mod p) .
p−1
Comece-se por provar (i), mostrando que se (1) tem solução então a (n,p−1) ≡ 1 (mod p).
Suponha-se que b ∈ Z é solução de (1). De bn ≡ a (mod p) e (a, p) = 1 conclui-se que
7
Teoria dos Números (2004/2005)
(bn , p) = 1 e portanto também (b, p) = 1. Assim, existe um e um só i ∈ {1, 2, . . . , p − 1}
tal que b ≡ g i (mod p) e
bn ≡ a (mod p) ⇔ g in ≡ g k (mod p) .
Sem perda de generalidade suponha-se que in ≥ k. Uma vez que p é primo e (g k , p) = 1,
g in ≡ g k (mod p) ⇔ p | g in −g k ⇔ p | g k g in−k − 1 ⇔ p | g in−k −1 ⇔ g in−k ≡ 1 (mod p) .
Mas a ordem de g módulo p é p − 1, logo
g in−k ≡ 1 (mod p) ⇔ p − 1 | in − k ⇔ in ≡ k (mod p − 1) .
Provou-se assim que b é solução de (1) se e só se existe i ∈ {1, 2, . . . , p − 1} tal que
b ≡ g i (mod p)
ni ≡ k (mod p − 1) .
e
Assim, se (1) tem solução então a congruência, de grau 1 e incógnita i, ni ≡ k (mod p−1)
tem solução, logo (n, p − 1) | k. Então
a
p−1
(n,p−1)
= g
k
p−1
(n,p−1)
k
(n,p−1)
= g
∈ N e, do Teorema de Fermat, obtém-se
k
(n,p−1)
p−1
≡ 1 (mod p) .
p−1
p−1
Prove-se agora (ii). Suponha-se que a (n,p−1) ≡ 1 (mod p), isto é, g k (n,p−1) ≡ 1 (mod p).
p−1
Então k (n,p−1)
é múltiplo da ordem de g, que é p − 1, e portanto (n, p − 1) divide k. Na
demonstração de (i) provou-se que b é solução de (1) se e só se existe i ∈ {1, 2, . . . , p − 1}
tal que b ≡ g i (mod p) e ni ≡ k (mod p−1). Uma vez que (n, p−1) divide k, a congruência
(de incógnita i) ni ≡ k (mod p − 1) tem exactamente (n, p − 1) soluções. Resta então
provar que se i1 e i2 são duas soluções distintas (isto é, incongruentes módulo p − 1) de
ni ≡ k (mod p − 1) então g i1 6≡ g i2 (mod p). Sejam i1 e i2 nessas condições e suponha-se
que i1 < i2 . Então, porque a ordem de g é p − 1,
g i1 ≡ g i2 (mod p) ⇔
p | g i1 (g i2 −i1 − 1)
⇔
p | g i2 −i1 − 1
⇔
g i2 −i1 ≡ 1 (mod p)
⇔ p − 1 | i2 − i 1
⇔ i1 ≡ i2 (mod p − 1) .
O processo de demonstração da proposição anterior fornece um método para resolver
congruências do tipo xn ≡ a (mod p), com p primo tal que p - a.
8
Teoria dos Números (2004/2005)
Vejam-se dois exemplos.
Exemplo. Considere-se a congruência x6 ≡ 4 (mod 19). 19 é primo e (4, 19) = 1, logo
pode aplicar-se a proposição anterior. Uma vez que
18
4 (6,18) = 43 = 16 × 4 ≡ (−3)4 (mod 19) ≡ −12 (mod 19) ≡ 7 (mod 19) 6≡ 1 (mod 19) ,
conclui-se que a congruência x6 ≡ 4 (mod 19) não tem solução.
Exemplo.
Considere-se a congruência x10 ≡ 3 (mod 13). 13 é primo e (10, 13 − 1) =
(10, 12) = 2. Além disso,
12
3 (10,12) = 36 = 33
2
≡ 12 (mod 13) ≡ 1 (mod 13) .
Pela proposição anterior a congruência tem (10, 12) = 2 soluções (existem exactamente
2 classes de congruência módulo 13 cujos elementos verificam a congruência). Conforme
visto num exemplo anterior 2 é uma raı́z primitiva módulo 13 e portanto {2, 22 , . . . , 212 }
é um sistema reduzido de resı́duos módulo 13. Procure-se k ∈ {1, 2, . . . , 12} tal que
2k ≡ 3 (mod 13).
21 ≡ 2 (mod 13), 22 ≡ 4 (mod 13), 23 ≡ 8 (mod 13) e 24 = 16 ≡ 3 (mod 13), logo pode
considerar-se k = 4 e x10 ≡ 3 (mod 13) ⇔ x10 ≡ 24 (mod 13).
Por outro lado, se x10 ≡ 3 (mod 13), do facto de se ter (3, 13) = 1 resulta que
(x10 , 13) = 1 e portanto também (x, 13) = 1. Então existe i ∈ {1, 2, . . . , 12} tal que
x ≡ 2i (mod 13) e
x10 ≡ 24 (mod 13) ⇔ 210i ≡ 24 (mod 13) ⇔ 13 | 210i − 24 ⇔ 13 | 24 210i−4 − 1
⇔ 13 | 210i−4 − 1 ⇔ 210i−4 ≡ 1 (mod 13)
Uma vez que a ordem de 2 módulo 13 é 12, 210i−4 ≡ 1 (mod 13) ⇔ 12 | 10i − 4.
Então as soluções de x10 ≡ 3 (mod 13) são as 2 classes de congruência módulo 13
que são da forma [2i ]13 , com i pertencente a qualquer uma das 2 classes de congruência
módulo 12 que são soluções da congruência, de grau 1, 10i ≡ 4 (mod 12). Uma vez que
10i ≡ 4 (mod 12) ⇔ 5i ≡ 2 (mod 6) ⇔ −i ≡ 2 (mod 6) ⇔ i ≡ 4 (mod 6) ,
as 2 classes de congruência módulo 12 que são soluções de 10i ≡ 4 (mod 12) são [4]12 e
[10]12 . Então as soluções de x10 ≡ 3 (mod 13) são [24 ]13 = [3]13 e [210 ]13 = [10]13 .
Observação. Se a não é primo com p então a ≡ 0 (mod p) e portanto (porque p é
primo), a congruência xn ≡ a (mod p) só tem uma solução, [0]p .