Resolução de Exercícios – Caderno 3 Módulo 7

Resolução de Exercícios – Caderno 3
Módulo 7: Tarefa de fixação, pg. 404.
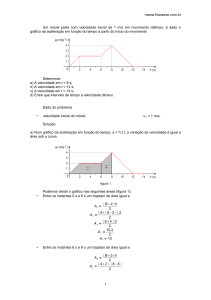
1) Do enunciado percebemos que em
(origem)
a) Em gráficos de
, quando calculamos o valor da tangente da reta, encontramos a
valor da aceleração. Outra explicação, matemática, é o calculo do coeficiente linear da
reta. Calculando pela tangente:
Obs.: a aceleração também pode ser calculada pela expressão:
Para calcular a velocidade inicial podemos escolher qualquer um dos dois pontos
mostrados no gráfico, construindo, assim uma função horária da velocidade naquele
ponto. Utilizaremos o primeiro ponto (10,34) então:
b) Velocidade:
Espaço:
2) Carro A: M.U.
Então:
, adotaremos como ponto de partida para o dois carros a
mesma posição, quer será a origem
, e como
, sendo assim:
Carro B: M.U.V.
Assim como o carro A,
,e
, pois parte do repouso. Então:
O exercício diz que no instante
os carros estão lado a lado, por isso
, então:
, substituindo o valor do tempo temos:
Alternativa B.
3) Perceba que no instante
os trens invertem seus valores de velocidade.
Outro fato importante é que a área de gráficos
é o , quando a área esta abaixo
do eixo do tempo, a velocidade é negativa, portanto o trem locomove-se afastando da
origem, por isso o
é negativo. Calculemos as áreas ( ) dos trens.
Trem A:
De 0 a 50 seg.:
De 50 a 150seg:
Portanto o trem A andou 125 m na direção positiva do deslocamento, em
seguida, voltou 250 m, sua posição é de
.
Trem B:
De 0 a 50 seg.:
De 50 a 150 seg.:
Já o tem B, primeiro voltou 125 m, depois progrediu 250 m, sua posição final é
de 125 m da origem.
Então a distância total entre eles é de
Alternativa D.
4) Visualmente notamos que o gráfico apresenta valor de aceleração positiva de 0 a 6
seg. (
), de 6 a 16 seg. a aceleração é nula
,
terminando com aceleração negativa de 16 a 20 seg (
).
a) Porém a pergunta faz referência ao valor da aceleração em módulo, portanto o menor
valor é quando
, ou seja, de 6 a 16 seg.
b) É máxima de 0 a 6 seg. conforme valores acima.
c) Área é igual ao .
Dividiremos a figura em dois trapézios:
I)
II)
De 0 a 16 seg. calculando a área:
De 16 a 20 seg. Calculando a área:
Finalizando:
d)
5)
;
a)
b)
e a altura do gráfico representa a velocidade final
mantém constante. Sabe-se que a área da figura é igual ao , então:
, pois se
c) Analisando o gráfico de 0 a 10 seg. percebemos que a aceleração é constante, pois o
gráfico é uma reta, então podemos calcular o valor da aceleração de 0 a 10 seg.
6) O gráfico é
, então quando calcularmos sua área encontraremos o valor do
que na verdade já foi dado
,
, a velocidade inicial é
, esse valor é a altura do trapézio representado pelo gráfico. O exercício
pede o tempo de reação
do motorista, que no gráfico é a base menor do trapézio,
sendo assim:
Alternativa C.
7)
a) Então a velocidade média é:
b) Sabe-se que o gráfico
;
ou
.
do movimento é da seguinte forma:
Como a aceleração e a desaceleração são constantes, possuem a mesma taxa, o
trapézio é regular. Precisamos então calcular os valores do tempo.
Então o gráfico ficará:
8)
. Calculando o valor da velocidade final:
b) Novamente a área do gráfico é o
, sendo assim:
Módulo 7, Série “O Pensador”, pg. 406.
1) a) Analisaremos no gráfico o tempo de 0 a 2 seg., pois no tempo 2 seg. a velocidade é
0 m/s, visto que no gráfico há a inversão do movimento. Outra informação que
percebemos neste mesmo intervalo de tempo, é a variação do espaço,
, e, portanto a velocidade inicial
é negativa. Façamos
então um gráfico do que foi discutido até agora.
Na figura vemos um triangulo, cuja área é o
, então:
Já a aceleração calculamos pela tangente do triângulo:
b) Portanto o gráfico final pode ser:
2)
para calcular a velocidade no instante 3,0 seg, precisamos então
encontrar os valores da aceleração
e da velocidade inicial
.
, pode-se interpretar no gráfico que o vértice esta no tempo igual 0, sendo
assim,
.
No ponto
do gráfico substituiremos os valores que possuímos para
encontrar
, então:
Substituindo os valores para
, teremos:
Outro modo de resolver o exercício é analisando a reta tracejada do gráfico. Essa
reta comporta-se como movimento uniforme, então, no ponto onde ela cruza a curva da
parábola os valores da velocidade são os mesmo. Para calcular a velocidade da reta,
simplesmente calcularemos o valor da tangente, então:
3) Analisando o gráfico podemos dividir a figura em 3 partes, conforme figuras abaixo:
Área da figura I (note que a velocidade esta em
em ):
e o tempo
Área da figura II:
Obs.: note que nessa figura a área pintada é exatamente a área
que foi desconsiderada da figura III, por isso os cálculos são
considerados corretos)
Área da figura III:
A área total:
.
Então o motorista estará no marco 22 km da rodovia.
4) Para resolver essa questão façamos o gráfico de como varia a aceleração, seguindo a
função:
e sabendo que
.
Para
.
Para
.
Para
Então o gráfico fica:
Calculando a área do gráfico encontraremos o :
Obs.: Neste caso fizemos a área do triângulo, pois para consideramos o trapézio
formado com o eixo do tempo, a aceleração deveria ter chego até o eixo, não chegou.
Diferente de gráficos acima do eixo do tempo, como o gráfico da questão 4 de fixação.
5) Essa questão resolvemos as questões a) e b) praticamente ao mesmo tempo, então:
a)
b)
: movimento uniforme e progressivo, com
e constante.
: M.U.V., progressivo, pois
, e retardado, pois
: repouso.
: M.U.V., progressivo, pois
, e acelerado, pois
6)
a) Sabido o valor da velocidade inicial
e também o valor da aceleração
para atingir a velocidade final, então:
Aceleração:
Freada
.
.
e da velocidade final
, fica simples calcular o tempo
:
b) Para melhor entender este gráfico observe a questão c):
c) O trajeto total de subida é de 354 m, nos trechos de aceleração e freada o espaço
percorrido é de:
Subtraindo os espaços percorridos na freada e subida, encontramos o espaço que
resta para o movimento uniforme:
.
Calculemos então o tempo em que o elevador fica em M.U.:
Então o tempo total:
7) Admitindo-se que ambos possuem o mesmo ponto de partida, então,
ambos.
Automóvel: Movimento Uniforme;
para
, então:
em 10 seg:
Motocicleta: Movimento Uniformemente Variado, até atingir a velocidade de:
.
Precisamos encontrar o espaço percorrido pela motocicleta nesses 10 segundos,
mas primeiro encontraremos a aceleração:
O espaço:
Então, nesse instante o automóvel esta a 250 m da origem com velocidade de 25
m/s. A motocicleta esta a 150 m da origem com velocidade de 30 m/s.
Poderíamos resolver igualando os espaços das duas funções horárias
mas nesse caso ambas as funções são de M.U.
Porém para relembrar, calcularemos por velocidade relativa, lembrando que a
motocicleta já esta em movimento uniforme, então:
Nesse caso o
é a diferença entre as posições dos dois móveis:
Para esse valor de tempo não se tem alternativa correta, então calculemos o ,
que a motocicleta percorreu.
Esse último valor encontrado refere-se ao tempo após chegar a velocidade
de
, que antes deste, já havia percorrido 150 m.
Então:
Alternativa D.
8) a) A velocidade inicial é zero
. Novamente a área de um gráfico
é
igual ao , sendo assim o valor da área acima do eixo dos tempos, tem que ser igual a
área abaixo deste mesmo eixo.
Área acima:
.
Como
, consequentemente a velocidade final será:
Área abaixo:
Como esta área começava em 8,0 seg. então o tempo total (T) para a velocidade
voltar a ser zero é:
b) O calculo da distância fica mais visível fazendo o gráfico da variação da velocidade
em função do tempo.
(figura fora de escala)
Calculando a área do trapézio acima: