energia sistemas conservativos

ENERGIA SISTEMAS CONSERVATIVOS
TEXTO PARA A PRÓXIMA QUESTÃO
(Ufpe 2007) Constantes físicas necessárias para a solução dos problemas:
aceleração da gravidade: 10 m/s£
constante de Planck: 6,6 x 10•¤¥ J.s
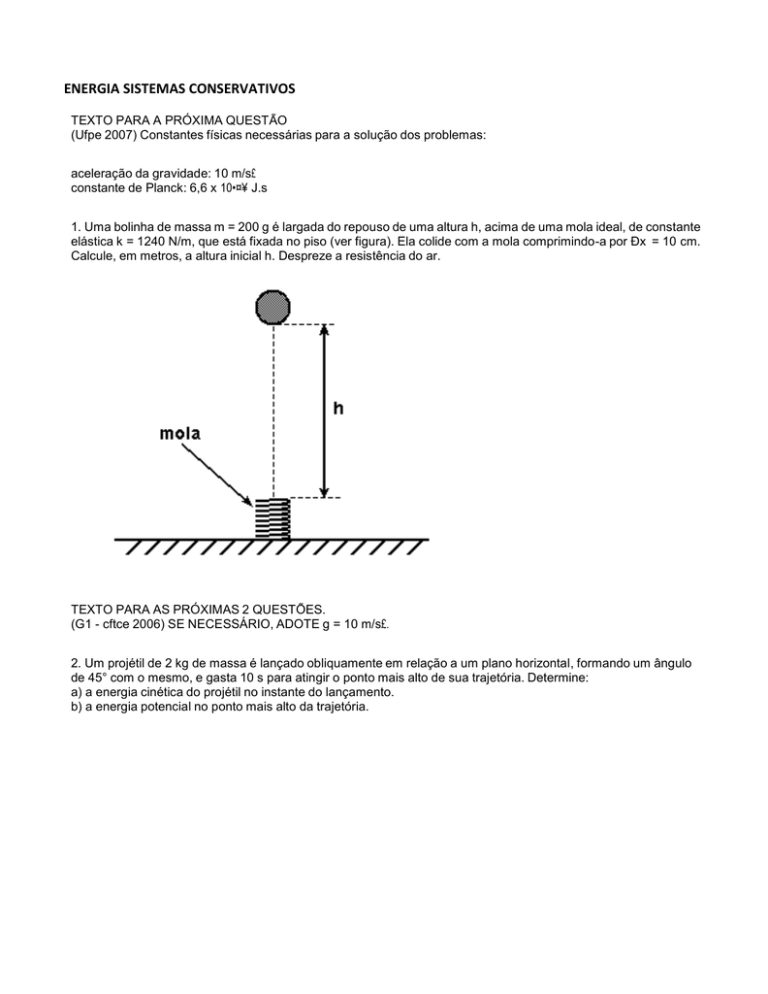
1. Uma bolinha de massa m = 200 g é largada do repouso de uma altura h, acima de uma mola ideal, de constante
elástica k = 1240 N/m, que está fixada no piso (ver figura). Ela colide com a mola comprimindo-a por Ðx = 10 cm.
Calcule, em metros, a altura inicial h. Despreze a resistência do ar.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES.
(G1 - cftce 2006) SE NECESSÁRIO, ADOTE g = 10 m/s£.
2. Um projétil de 2 kg de massa é lançado obliquamente em relação a um plano horizontal, formando um ângulo
de 45° com o mesmo, e gasta 10 s para atingir o ponto mais alto de sua trajetória. Determine:
a) a energia cinética do projétil no instante do lançamento.
b) a energia potencial no ponto mais alto da trajetória.
3. O bloco de massa m, da figura, desliza sem atrito com velocidade mínima necessária para subir a rampa de
altura h igual a 2,45m. Determine esta velocidade. (Despreze os atritos e considere g = 10 m/s£)
4. (Fuvest 98) Um brinquedo é constituído por um cano (tubo) em forma de 3/4 de arco de circunferência, de raio
médio R, posicionado num plano vertical, como mostra a figura. O desafio é fazer com que a bola 1, ao ser
abandonada de uma certa altura H acima da extremidade B, entre pelo cano em A, bata na bola 2 que se encontra
parada em B, ficando nela grudada, e ambas atinjam juntas a extremidade A. As massas das bolas 1 e 2 são M•
e M‚, respectivamente. Despreze os efeitos do ar e das forças de atrito.
a) Determine a velocidade v com que as duas bolas grudadas devem sair da extremidade B do tubo para atingir a
extremidade A.
b) Determine o valor de H para que o desafio seja vencido.
5. (Unesp 94) No esporte conhecido como "ioiô humano", o praticante, preso à extremidade de uma corda
elástica, cai da beira de uma plataforma para as águas de um rio. Sua queda é interrompida, a poucos metros da
superfície da água, pela ação da corda elástica, que tem a outra extremidade firmemente presa à beira da
plataforma. Suponha que, nas condições citadas acima, a distensão máxima sofrida pela corda, quando usado
por um atleta de peso 750 N, é de 10 metros, e que seu comprimento, quando não distendida, é de 30 metros.
Nestas condições:
a) A que distância da plataforma está o atleta, quando chega ao ponto mais próximo da água?
b) Qual o valor da constante elástica da corda?
(Despreze o atrito com o ar e a massa da corda, e considere igual a zero o valor da velocidade do atleta no início
da queda.)
6. (Fuvest 92) Adote: g = 10 m/s£
Uma mola pendurada num suporte apresenta comprimento igual a 20 cm. Na sua extremidade livre dependura-se
um balde vazio, cuja massa é 0,50 kg. Em seguida, coloca-se água no balde até que o comprimento da mola
atinja 40 cm. O gráfico a seguir ilustra a força que a mola exerce sobre o balde, em função do seu comprimento.
Pede-se:
a) a massa de água colocada no balde;
b) a energia potencial elástica acumulada na mola no final do processo.
7. (G1 - cftce 2005) Uma esfera de massa 1,2 kg, presa a uma mola de 1,0 m de comprimento e constante elástica
25N/m, descreve uma trajetória circular num plano horizontal sobre uma mesa perfeitamente polida, como mostra
a figura. Determine a energia mecânica, em relação à mesa, associada ao sistema massa-mola nas condições
citadas.
8. (G1) Como pode haver aumento de velocidade, se o aumento de velocidade significa aumento de energia
cinética, e a energia não aumenta pois se conserva?
9. (Unicamp 94) Uma bola metálica cai da altura de 1,0 m sobre um chão duro. A bola repica no chão várias vezes,
conforme a figura adiante. Em cada colisão, a bola perde 20% de sua energia. Despreze a resistência do ar (g =
10 m/s£).
a) Qual é a altura máxima que a bola atinge após duas colisões (ponto A)?
b) Qual é a velocidade com que a bola atinge o chão na terceira colisão?
10. (Unesp 95) Um bloco de madeira, de massa 0,40 kg, mantido em repouso sobre uma superfície plana,
horizontal e perfeitamente lisa, está comprimindo uma mola contra uma parede rígida, como mostra a figura a
seguir.
Quando o sistema é liberado, a mola se distende, impulsiona o bloco e este adquire, ao abandoná-la, uma
velocidade final de 2,0 m/s. Determine o trabalho da força exercida pela mola, ao se distender completamente:
a) sobre o bloco e
b) sobre a parede.
11. (Fuvest 95) A figura adiante representa um plano inclinado CD. Um pequeno corpo é abandonado em C,
desliza sem atrito pelo plano e cai livremente a partir de D, atingindo finalmente o solo. Desprezando a resistência
do ar, determine:
a) O módulo da aceleração 'a' do corpo, no trecho CD, em m/s£. Use para a aceleração da gravidade o valor g = 10
m/s£.
b) O valor do módulo da velocidade do corpo, imediatamente antes dele atingir o solo, em m/s.
c) O valor da componente horizontal da velocidade do corpo, imediatamente antes dele atingir o solo, em m/s.
12. (Unicamp 95) Numa câmara frigorífica, um bloco de gelo de massa m = 8,0 kg desliza sobre a rampa de
madeira da figura a seguir, partindo do repouso, de uma altura h = 1,8 m.
a) Se o atrito entre o gelo e a madeira fosse desprezível, qual seria o valor da velocidade do bloco ao atingir o solo
(ponto A da figura)?
b) Entretanto, apesar de pequeno, o atrito entre o gelo e a madeira não é desprezível, de modo que o bloco de
gelo e chega à base da rampa com velocidade de 4,0 m/s. Qual foi a energia dissipada pelo atrito?
c) Qual a massa de gelo (a 0 °C) que seria fundida com esta energia? Considere o calor latente de fusão do gelo
L = 80 cal/g e, para simplificar, adote 1 cal = 4,0 J.
13. (Unitau 95) No sistema indicado na figura a seguir, a mola ideal está com seu comprimento natural. Numa
primeira experiência, o apoio é baixado muito lentamente até abandonar o bloco. Numa segunda experiência o
apoio é subitamente retirado. Qual a razão entre as distensões máximas sofridas pela mola nas duas
experiências?
14. (Fuvest 92) O gráfico de velocidade de um corpo de 2 kg de massa em função do tempo é dado a seguir.
Durante todo intervalo de tempo indicado, a energia mecânica do corpo é conservada e nos instantes t = 0 e t = 25
s ela vale 100 J.
Pede-se:
a) o valor mínimo de energia potencial durante o movimento;
b) o gráfico da força resultante que atua sobre o corpo, em função do tempo.
15. (Unicamp 92) Um carrinho de massa m = 300 kg percorre uma montanha russa cujo trecho BCD é um arco de
circunferência de raio R = 5,4 m, conforme a figura adiante. A velocidade do carrinho no ponto A é vÛ = 12 m/s.
Considerando g = 10 m/s£ e desprezando o atrito, calcule;
a) a velocidade do carrinho no ponto C;
b) a aceleração do carrinho no ponto C;
c) a força feita pelos trilhos sobre o carrinho no ponto C.
16. (Fuvest-gv 91) Na figura a seguir, tem-se uma mola de massa desprezível e constante elástica 200 N/m,
comprimida de 20 cm entre uma parede e um carrinho de 2,0 kg. Quando o carrinho é solto, toda a energia
mecânica da mola é transferida ao mesmo. Desprezando-se o atrito, pede-se:
a) nas condições indicadas na figura, o valor da força que a mola exerce na parede.
b) a velocidade com que o carrinho se desloca, quando se desprende da mola.
17. (Fuvest 96) Um carro alegórico do bloco carnavalesco "Os Filhos do Nicolau" possui um plano inclinado e se
move com velocidade horizontal U constante em relação à pista. Albert, o filho mais moço, escorrega desde o alto
da rampa sem atrito. É observado por Galileu, o mais velho, sentado no carro, e por Isaac, parado na pista.
Quando Albert chega ao fim da rampa, Isaac observa que a componente horizontal da velocidade de Albert é
nula. Suponha que o movimento de Albert não altera a velocidade do carro, muito mais pesado do que ele.
São dados: H = 5,0 m, š = 30°. Adote g = 10 m/s£
a) Quais os valores das componentes horizontal Vh e vertical Vv da velocidade de Albert no fim da rampa,
observados por Galileu?
b) Quanto vale U?
c) Qual o valor da componente vertical Vv da velocidade de Albert no fim da rampa, observado por Isaac?
18. (Unesp 90) Um pássaro de massa igual a 1,0 kg, inicialmente em repouso no solo, alça vôo numa atmosfera
isotrópica. Sempre batendo asas, ele mantém velocidade escalar constante de 10 m/s e atinge 20 m de altura,
consumindo 75,0 calorias com os movimentos de seus músculos. Determine a energia dissipada pela resistência
do ar.
Considere: 1 cal ¸ 4 J e g = 10 m/s£.
19. (Ufpe 96) Uma balança usada para a pesagem de alimentos tem em sua base uma mola vertical de constante
elástica 50 N/m. Qual o valor, em Joules, da energia elástica armazenada na mola ao se pesar um prato com uma
massa total de 3,0 kg, depois que a mola atinge a posição de equilíbrio e permanece estacionária?
20. (Ufrj 96) Uma pequena esfera de aço está em repouso, presa por um fio ideal de 1,6 m de comprimento a um
suporte fixo. Num determinado instante, dá-se um impulso à esfera, de modo que ela adquira uma velocidade
horizontal ¬³, como ilustra a figura.
Despreze a resistência do ar e considere g = 10 m/s£.
Calcule o módulo de ¬³ para que, no ponto mais alto da trajetória, o módulo da tensão no fio seja igual à metade
do peso da esfera.
21. (G1) Qual é a função de uma caixa acústica?
22. (G1) Explique, em termos energéticos, o funcionamento de:
a) um escorregador
b) um sistema arco-flecha
c) uma usina hidrelétrica
23. (G1) Enuncie o princípio da conservação da Energia.
24. (G1) Uma montanha russa tem altura de 20 m. Considerando um carrinho de massa 100 kg, colocado
inicialmente no topo, calcule a Energia Potencial nesse momento, em relação ao solo.
25. (G1) Um carro de fórmula 1 chega a pesar 900 kg e encontra-se com velocidade x. Determine essa
velocidade, sabendo-se que sua Energia Cinética é de 3645000 J.
26. (G1) Explique o que é Energia Potencial Elétrica e Energia Potencial Química.
27. (G1) Explique o funcionamento de um telefone.
28. (G1) Uma bala de revólver de massa 0,02 kg tem uma velocidade de 100 m/s. Determine sua Energia
Cinética.
29. (G1) Quais são as transformações de energia que acontecem desde o instante em que você solta um tomate
maduro até o momento em que ele se espatifa no chão?
30. (G1) O que acontece com a energia elétrica consumida por um chuveiro elétrico?
31. (G1) Se você soltar uma bola de borracha de uma certa altura em relação ao solo verá que a bola atinge uma
altura MENOR após a colisão com o chão. Por que isso acontece?
32. (G1) O que afirma a lei da conservação da energia?
33. (G1) Quando um taco de golfe atinge uma bola o que acontece em termos de transferência de energia?
34. (G1) A figura a seguir mostra de forma esquemática a órbita do cometa Halley ao redor do Sol.
Do ponto de vista energético, como se pode explicar que o cometa aumenta de velocidade ao ir de A para P e
diminui de velocidade ao ir de P para A?
35. (G1) Uma usina hidrelétrica é mostrada esquematicamente a seguir.
Quais são as transformações de energia que nela ocorrem?
36. (G1) Em um dado ponto de um sistema um corpo possui 200 J de energia cinética e 500 J de energia
potencial. Qual o valor da energia mecânica desse corpo?
37. (G1) Em um dado ponto de um sistema um corpo possui 200 J de energia cinética e 500 J de energia
potencial. Se o valor da energia potencial passa para 400 J, qual o novo valor da energia cinética desse corpo?
38. (G1) Em um dado ponto de um sistema um corpo possui 500 J de energia cinética e 800 J de energia
potencial. Qual o valor da energia mecânica desse corpo, se a energia cinética passar a ser 100 J?
39. (Unesp 97) Um carrinho de 2,0 kg, que dispõe de um gancho, movimenta-se sobre um plano horizontal, com
velocidade constante de 1,0 m/s, em direção à argola presa na extremidade do fio mostrado na figura 1. A outra
extremidade do fio está presa a um bloco, de peso 5,0 N, que se encontra em repouso sobre uma prateleira.
Enganchando-se na argola, o carrinho puxa o fio e eleva o bloco, parando momentaneamente quando o bloco
atinge a altura máxima h acima da prateleira como mostra a figura 2.
Nestas condições determine:
a) a energia cinética inicial do carrinho;
b) a altura h, supondo que ocorra perda de 20% da energia cinética inicial do carrinho quando o gancho se prende
na argola. (Despreze quaisquer atritos e as massas das polias.)
40. (Unesp 97) Um carrinho, A, de massa m, e outro, B, de massa 2 m, mantidos em repouso sobre uma
superfície plana e horizontal, estão comprimindo uma mola, de massa desprezível, como mostra a figura a seguir.
Quando os carrinhos são liberados simultaneamente, a mola se distende, impulsionando-os, e B adquire, depois
que a mola estiver totalmente distendida, uma velocidade de 1,0 m/s.
a) Nessas condições, determine a velocidade adquirida por A.
b) Denominando hÛ e h½ as alturas máximas alcançadas, respectivamente, pelos carrinhos A e B, ao subirem as
rampas mostradas na figura, determine a razão hÛ/h½.
41. (Ufrj 97) A figura mostra o perfil JKLM de um tobogã, cujo trecho KLM é circular de centro em C e raio R=5,4m.
Uma criança de 15kg inicia sua descida, a partir do repouso, de uma altura h=7,2m acima do plano horizontal que
contém o centro C do trecho circular.
Considere os atritos desprezíveis e g=10m/s£.
a) Calcule a velocidade com que a criança passa pelo ponto L.
b) Determine a direção e o sentido da força exercida pelo tobogã sobre a criança no instante em que ela passa
pelo ponto L e calcule seu módulo.
42. (Ufrj 98) Uma pequena esfera metálica, suspensa por um fio ideal de comprimento Ø a um suporte, está
oscilando num plano vertical, com atritos desprezíveis, entre as posições extremas, A e B, localizadas a uma
altura h = Ø/2 acima do ponto mais baixo C de sua trajetória, como ilustra a figura a seguir.
Considere g = 10m/s£.
a) Calcule o módulo da aceleração da esfera nos instantes em que ela passa pelos pontos A e B.
b) Calcule o módulo da aceleração da esfera nos instantes em que ela passa pelo ponto C.
43. (Uerj 97) Um corpo de massa 2,0kg é lançado do ponto A, conforme indicado na figura, sobre um plano
horizontal, com uma velocidade de 20m/s. A seguir, sobre uma rampa até atingir uma altura máxima de 2,0m, no
ponto B.
Sabe-se que o calor gerado no processo foi todo absorvido pelo corpo e que um termômetro sensível, ligado ao
corpo, acusa uma variação de temperatura de 1°C.
a) Determine o calor específico médio do material que constitui o corpo, em J/kg°C
b) Indique se a altura máxima atingida pelo corpo, caso não houvesse dissipação de energia, seria maior, menor
ou igual a 2,0 m. Justifique sua resposta.
44. (Ufv 99) Uma esfera de massa "m", amarrada na extremidade de um cordão de comprimento "L", é lançada de
uma altura "h" com velocidade inicial, perpendicular ao cordão, de módulo "v³", conforme ilustra a figura a seguir.
Caso v³=Ë2gh, onde "g" é o módulo da aceleração da gravidade local, determine a altura máxima "H" atingida
pela esfera na inexistência de perdas de energia mecânica.
45. (Ufrj 2000) A figura mostra o perfil de um trilho vertical JKLM cujo trecho KLM é circular de centro em C e raio
R.
Um bloco de pequenas dimensões é abandonado a uma altura h=R/2 acima do plano horizontal que contém o
centro C e passa a deslizar sobre o trilho com atrito desprezível.
a) Determine a direção e o sentido da velocidade « do bloco no instante em que ele passa pelo ponto L e calcule
seu módulo em função de R e da aceleração da gravidade g.
b) Determine a direção e o sentido da resultante ù das forças que atuam sobre o bloco no instante em que ele
passa pelo ponto L (informando o ângulo que ela forma com a horizontal) e calcule seu módulo em função da
massa m do bloco e da aceleração da gravidade g.
46. (Ufg 2000) A energia potencial de um carrinho em uma montanha russa varia, como mostra a figura a seguir:
Sabe-se que em x=2m, a energia cinética é igual a 2J, e que não há atrito, sobre o carrinho, entre as posições x=0
e x=7m. Desprezando a resistência do ar, determine:
a) a energia mecânica total do carrinho;
b) a energia cinética e potencial do carrinho na posição x=7m;
c) a força de atrito que deve atuar no carrinho, a partir da posição x=7m, para levá-lo ao repouso em 5m.
47. (Unicamp 2001) Que altura é possível atingir em um salto com vara? Essa pergunta retorna sempre que
ocorre um grande evento esportivo como os jogos olímpicos do ano passado em Sydney. No salto com vara, um
atleta converte sua energia cinética obtida na corrida em energia potencial elástica (flexão da vara), que por sua
vez se converte em energia potencial gravitacional. Imagine um atleta com massa de 80kg que atinge uma
velocidade horizontal de 10m/s no instante em que a vara começa a ser flexionada para o salto.
a) Qual é a máxima variação possível da altura do centro de massa do atleta, supondo que, ao transpor a barra,
sua velocidade é praticamente nula?
b) Considerando que o atleta inicia o salto em pé e ultrapassa a barra com o corpo na horizontal, devemos somar
a altura do centro de massa do atleta à altura obtida no item anterior para obtermos o limite de altura de um salto.
Faça uma estimativa desse limite para um atleta de 2,0m de altura.
c) Um atleta com os mesmos 2,0m de altura e massa de 60kg poderia saltar mais alto? Justifique sua resposta.
48. (Ita 2002) Uma massa é liberada a partir do repouso de uma altura h acima do nível do solo e desliza sem
atrito em uma pista que termina em um "loop" de raio r, conforme indicado na figura. Determine o ângulo š relativo
à vertical e ao ponto em que a massa perde o contato com a pista. Expresse sua resposta como função da altura
h, do raio r e da aceleração da gravidade g.
49. (Uerj 2002) A mãe, para abrir uma janela tipo guilhotina, levanta totalmente um dos painéis dessa janela,
prendendo-o, então, por meio de uma trava de segurança. Os painéis são idênticos, medem 60cm de altura e têm
massa de 3kg cada.
Após um certo tempo, a trava se rompe e o painel cai sobre o peitoril da janela.
Desprezando atritos e a resistência do ar, calcule:
a) a energia mínima necessária para levantar totalmente o painel a partir do peitoril;
b) a velocidade com que o painel atinge o peitoril após o rompimento da trava de segurança.
50. (Unesp 2002) Um praticante de esporte radical, amarrado a uma corda elástica, cai de uma plataforma, a
partir do repouso, seguindo uma trajetória vertical. A outra extremidade da corda está presa na plataforma. A
figura mostra dois gráficos que foram traçados desprezando-se o atrito do ar em toda a trajetória. O primeiro é o
da energia potencial gravitacional, U (gravitacional), do praticante em função da distância y entre ele e a
plataforma, onde o potencial zero foi escolhido em y = 30m. Nesta posição, o praticante atinge o maior
afastamento da plataforma, quando sua velocidade se reduz, momentaneamente, a zero. O segundo é o gráfico
da energia armazenada na corda, U (elástica), em função da distância entre suas extremidades.
Determine:
a) o peso P do praticante e o comprimento L³ da corda, quando não está esticada, e
b) a constante elástica k da corda.
51. (Ufv 2001) Um corpo 1, de massa m•, parte do repouso de uma altura H e desliza sobre uma rampa até atingir
outro corpo 2, de massa m‚, que se encontra em repouso, conforme ilustrado na figura a seguir. Após a colisão, os
dois corpos, unidos um ao outro, movem-se até atingir um outra altura h.
Desprezando-se as dimensões dos corpos e efeitos de atrito de qualquer natureza, e denominando como g a
aceleração gravitacional local, expresse, em termos das constantes citadas:
a) A velocidade do corpo 1 imediatamente antes da colisão.
b) A velocidade dos dois corpos imediatamente após a colisão.
c) A altura h atingida pelos corpos.
52. (Ufg 2001) A figura mostra um pessoa com massa de 60kg que desliza, sem atrito, do alto de um tobogã de
7,2m de altura (ponto A), acoplando-se a um carrinho com massa de 120kg, que se encontra em repouso no
ponto B. A partir desse instante, a pessoa e o carrinho movem-se juntos na água, até parar. Considere que a força
de atrito entre o carrinho e a água é constante, e o coeficiente de atrito dinâmico é 0,10. A aceleração
gravitacional local é 10m/s£.
a) Calcule a velocidade do conjunto pessoa-carrinho, imediatamente após o acoplamento.
b) Calcule a distância percorrida na água pelo conjunto pessoa-carrinho, até parar.
53. (Uerj 2001) Um trapezista, de 70 kg, se solta do ponto de maior amplitude do movimento do trapézio, caindo
verticalmente de uma altura de 9,0 m na direção de uma rede de segurança. A rede se distende em 1,8 m e
lança-o de volta ao ar.
Supondo que nenhuma energia foi dissipada por forças não-conservativas, calcule a energia potencial da rede
totalmente distendida.
54. (Uerj 2001) Considere que fosse utilizada uma rampa de lançamento inclinada para impulsionar o
macaquinho.
Uma mola ideal, de coeficiente k e comprimento س=2Ë2m, é inicialmente comprimida até que o macaquinho fique
a uma altura h do solo.
O macaquinho se desprende da rampa no momento em que a mola volta à sua posição inicial de relaxamento, a
uma altura h³=4h/3 do solo.
Desprezando as forças não-conservativas e ÐE(gravitacional), determine o valor de k, de modo que o módulo da
velocidade inicial de lançamento seja igual a 20m/s.
Dado:
massa do macaquinho = 40 kg
55. (Unicamp 2003) Um cartaz de uma campanha de segurança nas estradas apresenta um carro acidentado
com a legenda "de 100 km/h a 0 km/h em 1 segundo", como forma de alertar os motoristas para o risco de
acidentes.
a) Qual é a razão entre a desaceleração média e a aceleração da gravidade, aÝ/g?
b) De que altura o carro deveria cair para provocar uma variação de energia potencial igual à sua variação de
energia cinética no acidente?
c) A propaganda de um carro recentemente lançado no mercado apregoa uma "aceleração de 0 km/h a 100 km/h
em 14 segundos". Qual é a potência mecânica necessária para isso, considerando que essa aceleração seja
constante? Despreze as perdas por atrito e considere a massa do carro igual a 1000 kg.
56. (Ufpe 2003) Um garoto desliza sobre um escorregador, sem atrito, de 5,0 m de altura. O garoto é lançado em
uma piscina e entra em contato com a água a uma distância horizontal de 2,0 m, em relação à borda. Calcule a
distância vertical h, entre a superfície da água e a borda da piscina. Dê sua resposta em cm.
57. (Ufpe 2003) Em um dos esportes radicais da atualidade, uma pessoa de 70 kg pula de uma ponte de altura
H=50 m em relação ao nível do rio, amarrada à cintura por um elástico. O elástico, cujo comprimento livre é L=10
m, se comporta como uma mola de constante elástica k. No primeiro movimento para baixo, a pessoa fica no
limiar de tocar a água e depois de várias oscilações fica em repouso a uma altura h, em relação à superfície do rio.
Calcule h, em m.
58. (Ufpe 2004) Um bloco de massa m = 0,1 kg comprime uma mola ideal, de constante elástica k = 100 N/m, de
0,2 m (ver figura). Quando a mola é liberada, o bloco é lançado ao longo de uma pista lisa. Calcule a velocidade
do bloco, em m/s, quando ele atinge a altura h = 1,2 m.
59. (Unesp 2004)
O gráfico da figura representa a velocidade em função do tempo de um veículo de massa 1,2 x 10¤ kg, ao se
afastar de uma zona urbana.
a) Determine a variação da energia cinética do veículo no intervalo de 0 a 12 segundos.
b) Determine o trabalho da força resultante atuando no veículo em cada um dos seguintes intervalos: de 0 a 7
segundos e de 7 a 12 segundos.
60. (Ufu 2004) João, em um ato de gentileza, empurra uma poltrona para Maria, que a espera em repouso num
segundo plano horizontal (0,8 m abaixo do plano de João). A poltrona tem uma massa de 10 kg e Maria tem uma
massa de 50 kg. O chão é tão liso que todos os atritos podem ser desprezados, conforme figura 1.
A poltrona é empurrada de A até B, partindo do repouso em A. João exerce uma força constante igual a 25 N, na
direção horizontal. Em B a poltrona é solta, descendo a pequena rampa de 0,8 m de altura. Quando a poltrona
chega com uma certa velocidade (v) em Maria, ela senta-se rapidamente na poltrona, sem exercer qualquer força
horizontal sobre ela, e o sistema poltrona + Maria escorrega no segundo plano horizontal, conforme figura 2.
Considerando a aceleração da gravidade como 10 m/s£, calcule:
a) o trabalho realizado por João no percurso AB.
b) a velocidade (v) da poltrona ao chegar em Maria.
c) a velocidade do sistema poltrona + Maria, após Maria sentar-se na poltrona.
61. (Ufrj 2005) Dois jovens, cada um com 50 kg de massa, sobem quatro andares de um edifício. A primeira
jovem, Heloísa, sobe de elevador, enquanto o segundo, Abelardo, vai pela escada, que tem dois lances por
andar, cada um com 2,0 m de altura.
a) Denotando por W(A) o trabalho realizado pelo peso de Abelardo e por W(H) o trabalho realizado pelo peso de
Heloísa, determine a razão W(A) / W(H).
b) Supondo que são nulas suas velocidades inicial e final, calcule a variação de energia mecânica de cada jovem
ao realizar o deslocamento indicado.
62. (Unicamp 2005) Num conjunto arco e flecha, a energia potencial elástica é transformada em energia cinética
da flecha durante o lançamento. A força da corda sobre a flecha é proporcional ao deslocamento x, como ilustrado
na figura.
a) Quando a corda é solta, o deslocamento é x = 0,6 m e a força é de 300 N. Qual a energia potencial elástica
nesse instante?
b) Qual será a velocidade da flecha ao abandonar a corda? A massa da flecha é de 50 g. Despreze a resistência
do ar e a massa da corda.
63. (Ufscar 2005) Quino, criador da personagem Mafalda, é também conhecido por seus quadrinhos repletos de
humor chocante. Aqui, o executivo do alto escalão está prestes a cair em uma armadilha fatal.
Considere que:
- o centro de massa do tubo suspenso, relativamente à parte inferior do tubo, está localizado a uma distância igual
à altura da cartola do executivo;
- a distância do centro de massa do tubo até o topo da cartola é 3,2 m;
- a vertical que passa pelo centro de massa do tubo passa também pela cabeça do executivo;
- o tubo tem massa de 450 kg e, durante uma queda, não sofreria ação significativa da resistência do ar, descendo
com aceleração de 10 m/s£;
- comparativamente à massa do tubo, a corda tem massa que se pode considerar desprezível.
a) Após esmagar a cartola, sem resistência significativa, com que velocidade, em m/s, o tubo atingiria a cabeça do
executivo?
b) Para preparar a armadilha, o tubo foi içado a 5,5 m do chão pela própria corda que posteriormente o sustentou.
Determine o trabalho, em J, realizado pela força peso na ascensão do tubo.
64. (Ufg 2006) Um bloco de massa igual a 0,5 kg é abandonado, em repouso, 2 m acima de uma mola vertical de
comprimento 0,8 m e constante elástica igual a 100 N/m, conforme o diagrama.
Calcule o menor comprimento que a mola atingirá. Considere g = 10 m/s£.
65. (Ufpe 2006) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma
altura h = 1,6 m. O bloco desliza, sem atrito, ao longo de uma superfície e colide, no ponto B, com uma mola de
constante elástica k=100 N/m (veja a figura a seguir). Determine a compressão máxima da mola, em cm.
66. (Ufpe 2006) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma
altura h = 0,8 m. O bloco desliza ao longo de uma superfície sem atrito e colide com um outro bloco, de mesma
massa, inicialmente em repouso no ponto B (veja a figura a seguir). Determine a velocidade do segundo bloco
após a colisão, em m/s, considerando-a perfeitamente elástica.
67. (Ufpe 2006) Um pequeno projétil, de massa m = 60 g, é lançado da Terra com velocidade de módulo V³ = 100
m/s, formando um ângulo de 30° com a horizontal. Considere apenas o movimento ascendente do projétil, ou
seja, desde o instante do seu lançamento até o instante no qual ele atinge a altura máxima. Calcule o trabalho, em
joules, realizado pela gravidade terrestre (força peso) sobre o projétil durante este intervalo de tempo. Despreze a
resistência do ar ao longo da trajetória do projétil.
68. (Ufpe 2006) Uma bolinha presa a um fio de comprimento L = 1,6 m que está fixado no teto, é liberada na
posição indicada na figura (ponto A). Ao passar pela posição vertical, o fio encontra um pino horizontal fixado a
uma distância h = 1,25 m (ver figura). Calcule o módulo da velocidade da bolinha, em m/s, no instante em que a
bolinha passa na altura do pino (ponto B).
69. (Ufpe 2006) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma
altura h = 0,8 m. O bloco desliza, sem atrito, ao longo de uma superfície e colide com um outro bloco, de mesma
massa, inicialmente em repouso no ponto B (veja a figura a seguir). Determine a velocidade dos blocos após a
colisão, em m/s, considerando-a perfeitamente inelástica.
70. (G1 - cftce 2004) Um atleta de esportes radicais, que pesa 800 N, pratica "bungee jumping" (salto com
elástico), saltando de uma ponte a 40 m de altura. O elástico usado tem 16 metros de comprimento e constante
elástica K. Partindo do repouso, o atleta cai, atingindo uma altura mínima de 8 m em relação ao solo. Determine o
valor da constante elástica K do elástico.
71. (Ufg 2007) Uma bolinha de massa m é lançada, por uma mola horizontal de constante elástica k, em uma
rampa lisa de ângulo de inclinação š com a horizontal que possui no topo uma curva de raio R, conforme figura
adiante.
A bolinha move-se rente a uma parede lisa perpendicular à rampa e, ao fazer a curva, passa por P, que se
encontra a uma altura H da base do plano, atingindo o ponto Q a uma distância D da vertical que passa por P.
Nessas condições, calcule:
a) A deformação da mola.
b) A força que a parede exerce sobre a bolinha no ponto mais alto da trajetória.
72. (Ufu 2007) O bloco 1 da figura a seguir possui massa m = 90Ë3 g e encontra-se conectado a duas molas
idênticas, podendo realizar um movimento oscilatório vertical, governado por um trilho vertical sem atrito.
O bloco 2 encontra-se preso a uma haste de massa desprezível, que pode girar em torno do ponto P da figura, e
está inicialmente em repouso na posição horizontal (posição C da figura).
a) O bloco 1 encontra-se, inicialmente, em equilíbrio na posição A, com as molas formando um ângulo š = 30° com
a direção vertical, conforme a figura apresentada. Nessa situação, cada mola distendeu 10 cm em relação ao seu
comprimento natural. Considerando g = 10 m/s£, determine, nessas condições: a constante elástica de cada mola.
b) Posteriormente, o bloco 1 é puxado para baixo e abandonado, adquirindo um movimento de encontro ao bloco
2. Imediatamente antes de colidir (elasticamente) com o bloco 2, o bloco 1 possui uma velocidade igual a 2Ë3 m/s
, entrando em repouso imediatamente após a colisão. Nessas condições, determine:
B1 - a máxima altura que o bloco 2 irá atingir até parar (posição D na figura), sabendo-se que o ângulo que a haste
forma com a horizontal nessa situação vale ‘ = 30°.
B2 - a aceleração angular do bloco 2 no instante em que pára (posição D na figura).
73. (G1 - cftce 2007) Uma esquiadora, de massa 50 kg, percorre as trajetórias I, II e III, partindo do repouso e do
mesmo ponto.
Despreze os atritos, a resistência do ar e adote g = 10 m/s£.
a) Qual o trabalho realizado pela força peso da esquiadora em cada trajeto?
b) Compare a potência desenvolvida pela esquiadora, ao passar pelos pontos A, B e C, sabendo que, nesses
pontos, sua velocidade tem a mesma direção.
74. (Ufc 2008) A figura a seguir descreve a situação inicial de um sistema onde duas molas estão comprimidas por
uma massa M, com seus comprimentos somados resultando L . As molas têm constantes elásticas k• e k‚ , sendo
que k• = 2k‚ , seus comprimentos sem deformação somados resultam 2 L, e as molas possuem massas
desprezíveis. Posteriormente, o sistema é liberado, e a massa M é lançada. Desconsidere atritos.
a) Calcule a energia armazenada no sistema na situação inicial.
b) Determine a velocidade da massa M quando ela perde o contato com o sistema de molas, em termos das
grandezas L , M, e k‚ (ou k•).
75. (Uepg 2008) Com base na figura a seguir, calcule a menor velocidade com que o corpo deve passar pelo
ponto A para ser capaz de atingir o ponto B. Despreze o atrito e considere g = 10 m/s£.
76. (G1) Definindo numa só palavra, energia cinética é energia de
potencial é energia
.
_, enquanto que energia
77. (G1) Dê um exemplo de uma situação em que a energia potencial elástica se transforma em energia cinética
ou vice-versa.
78. (G1) Nas antigas locomotivas queimava-se carvão para obter a energia necessária para movê-las. Antes de
ser energia cinética da locomotiva, onde estava a energia? Que tipo de energia era?
79. (Ufpe 2004) Um bloco de massa m• = 100 g comprime uma mola de constante elástica k = 360 N/m, por uma
distância x = 10,0 cm, como mostra a figura. Em um dado instante, esse bloco é liberado, vindo a colidir em
seguida com um outro bloco de massa m‚ = 200 g, inicialmente em repouso. Despreze o atrito entre os blocos e o
piso. Considerando a colisão perfeitamente inelástica, determine a velocidade final dos blocos, em m/s.