Retificadores monofásicos controlados de meia - metaheuro

Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
Retificadores com tiristores
2.1 O retificador controlado monofásico de meia onda
a) Carga Resistiva com Força Contra-eletromotriz CC
Quando a carga possui uma força contra-eletromotriz de corrente contínua
(CC), o tiristor somente entrará em operação se a tensão entre anodo e catodo
do mesmo for maior que zero (
e se houver gatilhamento. Portanto se
houver disparo do tiristor, mas (
não circulará corrente pelo tiristor.
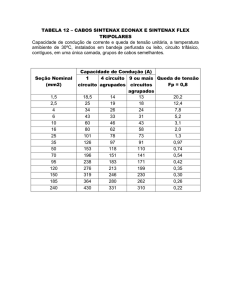
Figura 2.3 a Retificador com carga resistiva e FCEM
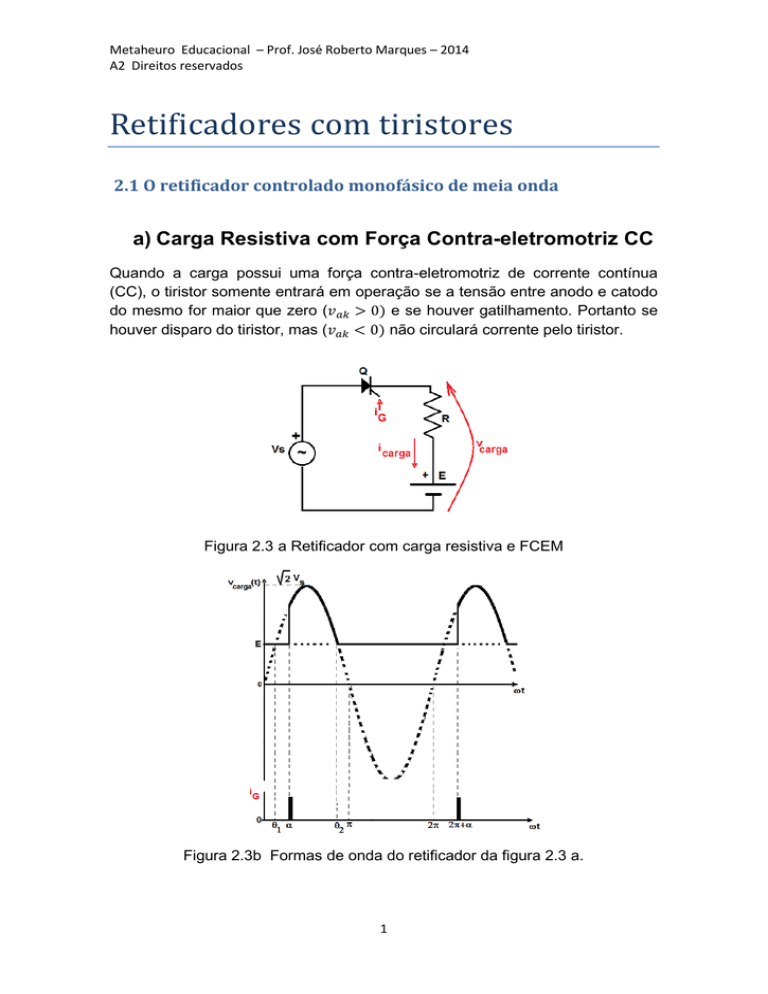
Figura 2.3b Formas de onda do retificador da figura 2.3 a.
1
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
A figura 2.3b mostra que o menor valor possível de disparo do tiristor ocorre
quando α=θ1,ou seja quando a tensão da fonte CA iguala a tensão da fonte
CC. Neste ponto o valor do ângulo mínimo de disparo é
. E o ângulo de extinção a corrente é
(rad), que
corresponde também ao valor máximo de α. Com isso podemos deduzir os
valores de mérito do circuito.
Tensão média na carga (
:
A tensão média na carga pode ser obtida pela equação (2.19).
(2.19)
Corrente média na carga (
A corrente média na carga pode ser obtida por processo direto utilizando a lei
de Ohm, como mostra a expressão (2.20).
(2.20)
Corrente eficaz na carga (
A corrente eficaz na carga é obtida pela expressão (2.21)
(2.21)
A potência média na carga (
A potência média na carga corresponde a potência dissipada pelo resistor por
efeito joule, como mostra a expressão (2.22).
(2.22)
A potência aparente do gerador pode ser calculada diretamente, já que
.
b) Carga RL com Força Contra-eletromotriz CC
No caso de cargas RL com FCEM, o armazenamento de energia no campo
magnético do indutor força o ângulo de extinção da corrente para além do
ponto θ2 estudado no caso anterior, porém o ângulo de disparo do tiristor
ocorre sob as mesmas condições do me smo caso. Assim o tiristor somente
2
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
pode entrar em operação se
e houver aplicação de um pulso de
corrente em seu terminal de gatilho e o ângulo de extinção da corrente
dependerá de α, φ e da relação
. As formas de onda do circuito são
mostradas nas figuras 2.4.
Utilizando o princípio da superposição, obtemos as correntes de regime das
duas fontes, para a fonte CA a corrente de regime é a mesma estudada no item
(c) ou seja
, das mesma forma a corrente de
regime da fonte CC é dada por
dada por
e a corrente transitória é
, que reunidas fornecem a expressão (2.23).
(2.23)
Figura 2.4a Retificador monofásico com carga RL e FCEM CC
Figura 2.4b Formas de onda relativas ao circuito da figura 2.4b
3
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
Que existe no intervalo (α,β) de um ciclo da rede CA e fora desse intervalo é
zero. Rearranjando a equação (2.23) obtemos a equação (2.24).
(2.24)
O valor da constante A2 pode ser determinado a partir da condição inicial, que
devido a presença do indutor em série com o circuito é imediata, ou seja,
. De onde obtemos a expressão (2.25).
(2.25)
Assim
(2.26)
Portanto a corrente que flui no circuito no intervalo (α,β) é dada pela expressão
(2.27).
(2.27)
Essa corrente é zero quando ωt = β, como mostra a figura 2.4b e neste ponto a
tensão da fonte CC volta a prevalecer na carga. A partir desse ponto obtemos a
expressão (2.28) que permite o cálculo do ângulo de extinção β com a
utilização do método de Newton-Rapson.
(2.28)
A transformação do fator
é mostrada na figura 2.5.
4
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
Figura 2.5 Relações entre impedância, a reatância indutiva e a resistência do
circuito da figura 2.4a.
Para a aplicação do método de Newton-Rapson na expressão (2.28) ,temos as
expressões (2.29) e (2.30).
(2.29)
(2.30)
Os valores de mérito que definem o comportamento desse circuito são:
Tensão média na carga (
:
A tensão média na carga pode ser obtida pela equação (2.17).
(2.29)
Corrente média na carga (
A corrente média na carga pode ser obtida por processo direto utilizando a lei
de Ohm, como mostra a expressão (2.18).
(2.30)
Corrente eficaz na carga (
A corrente eficaz na carga é obtida pela expressão (2.31)
5
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
(2.31)
A potência média na carga (
A potência média na carga corresponde a potência dissipada pelo resistor por
efeito joule, como mostra a expressão (2.32).
(2.32)
Com base no conhecimento da corrente eficaz do gerador a potência aparente
do gerador pode ser prontamente calculada
.
Exercícios resolvidos.
1) Dado o circuito abaixo, determinar :
a) O ângulo de condução de corrente no diodo
b) A corrente média na carga.
c) A corrente eficaz na carga
d) A tensão média na carga
e) A tensão eficaz na carga
f) O fator de potência visto pela fonte
g) Esboce as formas de onda da corrente e da tensão na carga
Aplicando o princípio da superposição ao circuito obtemos:
6
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
Devido a fonte de tensão em regime:
Devido a fonte CC
Adicionando as duas situações e o efeito transitório temos para o intervalo
:
Observando que o diodo inicia sua condução apenas quando a tensão da fonte CC é superada
pela tensão de fonte CA, ou seja quando
então do a presença do indutor
. O valor do ângulo de condução inicial é
.
Substituindo na equação original:
Onde t0=0.
Fazendo
and
Calculando valores a partir dos dados temos:
Portanto:
Calculando o ângulo de extinção da corrente:
7
podemos escrever:
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
Admitindo o valor inicial de
8
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
O ângulo de condução de corrente no diodo é:
A corrente média na carga é:
A corrente eficaz é:
9
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
A tensão média na carga é:
A tensão eficaz na carga é:
O fator de potência em relação a carga é:
2Q) Dado o circuito abaixo, determinar :
a) O ângulo de condução do diodo
b) A corrente média na carga.
c) A corrente eficaz na carga
d) A tensão média na carga
e) A tensão eficaz na carga
f) O fator de potência visto pela fonte
g) Esboce as formas de onda da corrente e da tensão na carga
10
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
O diodo apenas conduz quando a tensão da rede supera a tensão da fonte CC, portanto o
ângulo inicial de condução é:
O ângulo final de condução ocorre quando a tensão da fonte CA fica menor que a do que a
tensão CC, e por simetria pode ser calculada por:
O ângulo de condução do diodo é:
Durante a condução, no intervalo,
a corrente que circula no circuito é
dada por:
A corrente média na carga pode ser calculada pela expressão:
A corrente eficaz na carga é:
11
Metaheuro Educacional – Prof. José Roberto Marques – 2014
A2 Direitos reservados
A tensão média na carga é:
A tensão eficaz na carga é:
O fator de potência visto pela carga é:
12