Exemplos de aplicação das leis de Newton e Conservação do

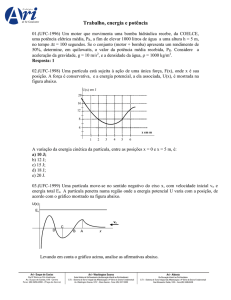
Exemplos de aplicação das leis de Newton e
Conservação do Momento Linear
Cálculo de resultante I
Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante.
𝑭𝟏 = 10 N
y
30
x
𝑭𝟐 = 5 N
Passo 1: definir o sistema de coordenadas a ser utilizado.
Pela simetria do problema, vamos definir um sistema de
eixos composto por um eixo na horizontal e outro na
vertical da figura.
𝑭𝟑 = 8 N
Passo 2: calcular as componentes de cada força ao longo dos eixos de coordenadas escolhido.
Neste caso, as forças F2 e F3 estão , respectivamente ao longo dos eixos x e y. A força F1 tem
parte de sua ação ao longo do eixo x (F1x) e parte de sua ação ao longo do eixo y (F1y). Podemos
escrever então, que:
𝐹𝑟𝑥 = 𝐹2 + 𝐹1𝑥
𝐹𝑟𝑦 = 𝐹3 + 𝐹1𝑦
Cálculo de Resultante II
Passo 3: vamos calcular as componentes da força F1 ao longo de cada um dos eixos:
𝐹1𝑥 = 𝐹1 cos 330 = 10 × 0,87 = 8,7 𝑁
𝐹1𝑦 = 𝐹1 sen 330 = 10 × (−0,5) = −5 𝑁
Logo, as componentes da força resultante serão dadas por:
𝐹𝑟𝑥 = 𝐹2 + 𝐹1𝑥 = 8,7 𝑁 + 5𝑁 = 13,7𝑁
𝐹𝑟𝑦 = 𝐹3 + 𝐹1𝑦 = 8𝑁 − 5𝑁 = 3𝑁
Portanto, a força resultante será escrita como:
𝐅𝑟 = 13,7𝐢 + 3𝐣
Cálculo de força resultante II
O Plano inclinado
N
Queremos calcular a força resultante sobre o
bloco de massa m. Neste caso, a simetria do
problema sugere a orientação dos eixos
conforme a figura.
m
P
α
O principal problema aqui é visualizar o ângulo que a força peso faz com a vertical. Um
pouco de geometria nos mostra que:
𝑃𝑥 = 𝑃𝑠𝑒𝑛(α) = 𝑚𝑔𝑠𝑒𝑛(α)
𝑃𝑦 = −𝑃𝑐𝑜𝑠 α = − 𝑚𝑔𝑐𝑜𝑠(α)
α
π/2 -α
α
Cálculo de força resultante II
O Plano inclinado
Portanto, as componentes da força resultante serão dadas por:
𝐹𝑟𝑥 = 𝑃𝑥 = mg sin 𝛼
𝐹𝑟𝑦 = 𝑁 + 𝑃𝑦 = 𝑁 − 𝑚𝑔 cos 𝛼=0 N
Logo, a força resultante tem somente componentes na direção x:
𝐅𝑟 = mg sin 𝛼 𝐢
Cálculo de força resultante
Usando a ação e reação
Considere dois blocos ligados da maneira mostrada na figura. Sobre o bloco 1 atua
uma força F. Calcule a aceleração sobre os dois blocos considerando que a corda que
liga os dois é inextensível.
m1
T2
T1
F
m2
Neste caso, temos duas forças formando um
par de ação e reação.
Observe que a única força que age no
bloco de massa m1 é a força T2 devida
ao bloco 2.
Cálculo de força resultante
Usando a ação e reação
Vamos equacionar as forças atuando nos dois blocos:
𝐹𝑟1 = 𝑇2 = 𝑚1 𝑎
𝐹𝑟2 = 𝐹 − 𝑇1 = 𝑚2 𝑎
Corda inextensível
implica iguais
acelerações nos dois
blocos
Vamos usar agora o fato de que as duas forças T1 e T2 formam um par de ação e
reação: T1 = T2.
𝐹𝑟1 = 𝑇1 = 𝑚1 𝑎
𝐹𝑟2 = 𝐹 − 𝑇1 = 𝑚2 𝑎
Isolando agora para a aceleração:
𝑎=
𝐹
𝑚2 + 𝑚1
Peso aparente
Considere a seguinte situação: uma pessoa está dentro de um elevador que desce a uma
velocidade de 10, 0 m/s e leva 25 m para parar. Considere que a massa da pessoa seja de
70 kg e a massa do elevador de 730 kg. Calcule a aceleração com a qual o elevador é
levado ao repouso e o peso que uma balança marcaria para o peso da pessoa dentro do
elevador.
y
Primeiro, vamos calcular a aceleração do conjunto, sob a hipótese
de que a aceleração foi constante. Neste caso, podemos usar a
equação de Torricelli para calcular a aceleração:
N
a
Pp
Balança
v 2f  vi2  2a( y f  yi )
0   10m / s 
a

2( y f  yi )
2  (0  25)
v 2f  vi2
Pe
100
a  m / s 2  2m / s 2
50
2
Peso aparente
Vamos agora calcular o peso aparente da pessoa sobre o elevador. Sobre a pessoa
atuam duas forças:
1) O peso da pessoa;
2) A força de reação da balança sobre ela, chamada de Normal.
Observe que a Normal é, em módulo, igual à força que a pessoa aplica sobre a
balança que é o peso medido pela balança.
Logo:
Fr = P  N  ma y  N  mg
N  m( a y  g )
N  70kg  (2  9,81)m / s 2
N  70kg 11,81m / s 2
N  826, 7 N
Peso medido pela balança.
Interregno – Energia cinética e
conservação da energia
Definimos a Energia Cinética de uma partícula de massa m e velocidade de módulo
v por:
1
𝐸𝑐 = 𝑚𝑣 2
2
Esta quantidade nos indica quanto de movimento uma partícula tem. Ela é relacionada
com a distância na qual uma força agiu para levar a partícula de uma situação na qual a
velocidade da partícula era zero até a situação na qual a velocidade da partícula é v.
Distância percorrida sob a ação da força F
m
Posição inicial
(v=0).
F
Posição na qual a
velocidade é v.
Interregno – Conservação da
Energia
Em um sistema fechado a energia total,
entendida como a soma das energias de
todas as partículas é conservada.
Em sistemas fechados, em qualquer processo, a energia total antes
de o processo ocorrer é a mesma depois de o processo ocorrer.
Colisões em uma dimensão
Problema: qual serão as velocidades das duas bolas após a colisão?
Posição do choque
Posição do choque
m, v1f
m, v1i = 0
M, V2i
Situação antes do choque
M, V2f
Situação depois do choque
Pti  Ptf
Eti  Etf
Hipótese: o choque é completamente elástico: a energia não é perdida de forma alguma.
Princípios que podemos aplicar:
•Conservação do momento;
•Conservação da energia.
Eq. 1
Colisões em uma dimensão
O momento linear total do sistema antes do choque é dado por:
Pti  p1i  p2i
Pti  mv1i  M V2i
Estamos no caso
unidimensional
Pti  mv1i  M V2i  M V2i
O momento linear total do sistema após o choque é dado por:
Ptf  p1 f  p2 f
Ptf  mv1 f  M V2 f
Ptf  mv1 f  M V2 f
Portanto, podemos escrever a partir da conservação do momento linear:
Pti  Ptf
M V2i  mv1 f  M V2 f
M V2i  M V2 f  mv1 f
v1 f 
M
m
V
2i
 V2 f

Colisões em uma dimensão
Da conservação da energia temos:
Eci  Ecf
1
1
1
MV22i 
mv12f 
MV22f
2
2
2
Vamos agora isolar a velocidade final da partícula que estava inicialmente em
repouso, vf em função da velocidade da partícula que estava inicialmente em
movimento:
V
2i
1
1
1
MV22i 
mv12f 
MV22f
2
2
2
1
1
1
MV22i 
MV22f 
mv12f
2
2
2
1
1
2
2

M 
V

V

mv12f
2
i
2
f


2
2
m 2
2
2


V

V

v1 f
2
i
2
f


M
m 2
 V2 f  V2 i  V2 f  
v1 f
M
Colisões em uma dimensão
Usando agora a Eq. 1:
V
 V2 f
 V
 V2 f

V
 V2 f
 V
 V2 f

2i
2i
2i
2i
V2 i  V2 f
M 

V2 f  1 

m 

mM
V2 f
m
m M

V2 i  V2 f

M 
m

2
M

V

V
 2i
2 f 
m
M

V2i  V2 f 
m
 M

 V2 i 
 1
 m

M m
 V2 i
m
V2 f  V2 i
M m
M m
 
2
Colisões em uma dimensão
Usando agora esta expressão, podemos obter a velocidade final da partícula
inicialmente em repouso:
M
V2i  V2 f 
m
M 
M m

V2i  V2i

m 
M m

M
M m


V2i 1 
m
M m


M
M m M m
M
2m

V2i
 V2i
m
M m
m M m
v1 f 
v1 f
v1 f
v1 f
v1 f  2V2i
M
M m
Colisões em uma dimensão – casos
limite
i) Massas iguais: M = m
Nesse caso:
v1 f  2V2i
V2 f  V2i
M
m
m
 2V2i
 2V2i
 V2i
M m
mm
2m
M m
mm
 V2i
 0
M m
M m
Há uma transferência completa de momento da partícula que se
movimenta para aquela que está parada !
Colisões em uma dimensão – casos
limite
ii) Massa da partícula alvo é muito menor que a massa da partícula projétil:
M >> m (Projétil pesado)
Agora temos:
v1 f  2V2i
V2 f  V2i
M
M
 2V2i
 2V2i
M m
M
M m
 V2i
M m
O momento do projétil não é praticamente modificado !
Colisões em uma dimensão – casos
limite
iii) Massa da partícula alvo é muito maior que a massa da partícula projétil: m >> M
(Alvo pesado)
v1 f  2V2i
V2 f  V2i
M
M
 2V2i
1
M m
m
M m
m
 V2i
 V2i
M m
m
Nesse caso a partícula projétil inverte simplesmente a sua velocidade e a
partícula alvo se move com velocidade muito pequena para a frente.