Experiências de Joule (1840 a 1849)

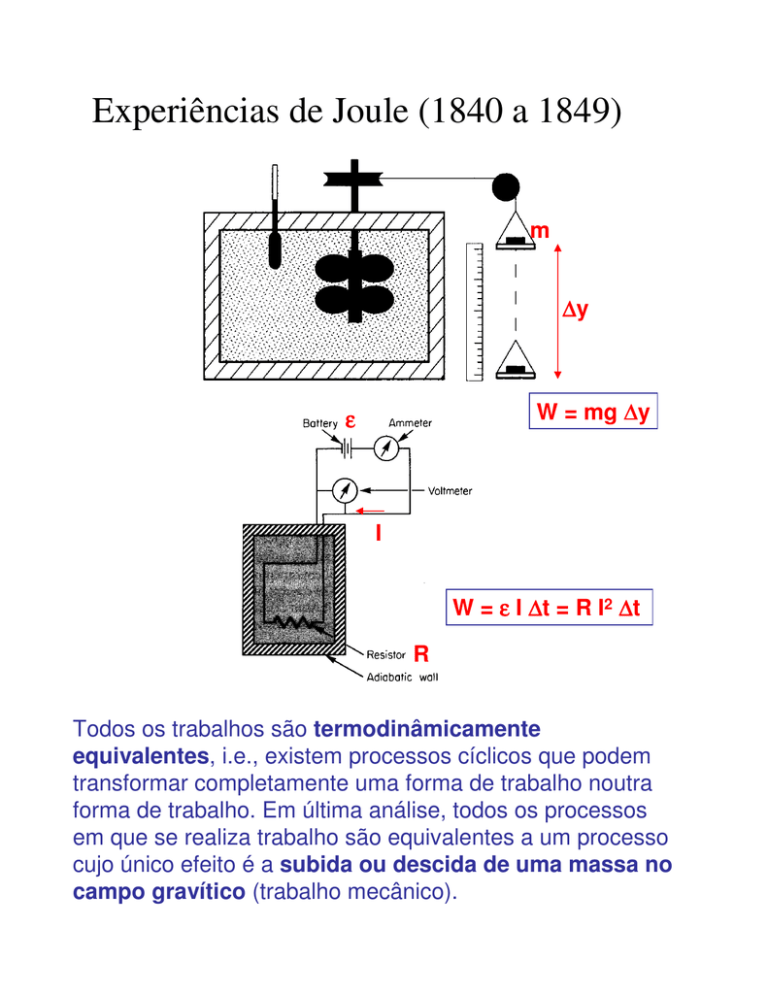
Experiências de Joule (1840 a 1849)
m
∆y
W = mg ∆y
ε
I
W = ε I ∆t = R I2 ∆t
R
Todos os trabalhos são termodinâmicamente
equivalentes, i.e., existem processos cíclicos que podem
transformar completamente uma forma de trabalho noutra
forma de trabalho. Em última análise, todos os processos
em que se realiza trabalho são equivalentes a um processo
cujo único efeito é a subida ou descida de uma massa no
campo gravítico (trabalho mecânico).
Primeira Lei da Termodinâmica
I. Def. termodinâmica de energia interna
do sistema
O trabalho adiabático sobre um sistema termodinâmico
(com energia cinética de conjunto e energia potencial externa
constantes) só depende dos estados inicial e final e não
do processo realizado entre esses dois estados.
Existe, por isso, a função de estado energia interna tal que
W adia = U
f
− U i = ∆U
Implicações:
A diferencial δWadia = dU é uma diferencial
exacta, no sentido em que
δW =0
adia
II. Def. termodinâmica de calor
Num processo não-adiabático, o trabalho realizado sobre um
sistema termodinâmico é diferente do trabalho adiabático
realizado entre os mesmos estados inicial e final. A diferença
entre ambos é o calor trocado durante o processo:
Q = W adia − W ⇔ Q = ∆ U − W ⇔ ∆ U = W + Q
Calor e Trabalho
A energia interna de um sistema pode variar:
por trocas de trabalho com a vizinhança
(processos redutíveis a um processo mecânico:
a subida ou descida de uma massa no campo
gravítico)
por trocas de calor com a vizinhança (processos
não redutíveis a um processo mecânico)
Calor (Q) e trabalho (W) são funções de processo às quais
correspondem diferenciais inexactas. Já a energia interna, U, é uma
função de estado (ou de ponto) à qual corresponde uma diferencial
exacta.
Princípio de Equivalência entre
Calor e Trabalho
A partir do trabalho experimental de Joule:
1 cal = 4,19 J
(caloria: calor transferido para 1g de água, num processo em que a sua
temperatura aumenta de 1ºC (e não é realizado trabalho, claro!)
Para 2 processos diferentes (I e II) que levem o
sistema do mesmo estado i ao mesmo estado f:
∆U = U f − U i = QI + WI = QII + WII
⇔ QI − QII = WII − WI
Forma diferencial da 1ª Lei (processo
infinitesimal):
dU = δW + δQ
Processo infinitesimal quase-estático e
sistema PVT:
dU = − PdV + δQ
Processo finito quase-estático e sistema PVT:
f
f
dU = U f − U i = − PdV + Q
i
i
Capacidade térmica
T → T+∆T
Quantidade de calor que é necessário
fornecer ao sistema (de forma quaseestática), para que a temperatura do
sistema aumente de 1 kelvin.
Q
δQ
C = lim
=
∆T → 0 ∆ T
dT
Sistema
Q
Mas a quantidade de calor fornecida é uma função do processo
(ou caminho) ...
CP =
CV =
γ =
δQP
dT P
δ QV
dTV
CP
CV
=
=
δQ
dT
→ capacidade térmica a pressão constante
P
δQ
dT
→ capacidade térmica a volume constante
V
→ coeficiente adiabático
C é uma grandeza extensiva. Define-se também:
c=
C
n
Capacidade térmica molar
e
c=
C
m
Capacidade térmica mássica