.0.40 A i Ni lHm = ⇒ =

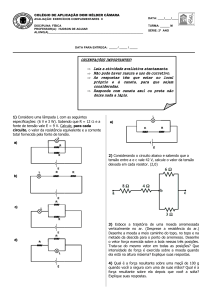
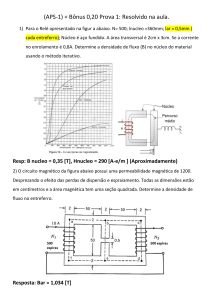
CONVERSÃO ELETROMECÂNICA DE ENERGIA – Lista de exercícios sobre histerese magnética
(a) Suponha que o ímã tem uma densidade inicial de
fluxo igual a zero. Determine o valor máximo da
corrente i da bobina necessária para fazer o ímã
operar na sua densidade de fluxo residual Br=1,35 T.
Figura 1 - Fabricação de agulhas imantadas para uso
em bússolas. A China produz aços de ótima qualidade
desde o século V d.C.
Questão
[adaptação, problema 2.34 Slemon]
Um bloco retangular de ímã permanente deve ser
magnetizado usando-se a montagem mostrada na
figura abaixo.
(b) Determine a energia necessária para levar o ponto
de operação do ímã de (0 ; 0) até (1,35 ; 0).
(c) Um método simples de magnetização de um ímã
consiste em conectar um capacitor carregado à bobina
mostrada na montagem acima. Considere a montagem
com um capacitor de 100 µF. Para que tensão o
capacitor estaria carregado para fornecer a corrente de
magnetização necessária?
2
W c=1/2CV
(d) O método de magnetização discutido no item (c)
produz uma corrente oscilatória, típica de um circuito
LC. Essa corrente pode desmagnetizar o ímã. Mostre
como a utilização de um simples retificador pode evitar
essa desmagnetização.
Discussão
a) Para produzir o Hmax, 80.000 A/m, a corrente
necessária é obtida pela Lei Circuital de Ampère.
Como se assume que o material doce tem
permeabilidade infinita, o ímã está em curtocircuito.
H max lm = Nimax ⇒ imax = 40.0 A.
O bloco tem um comprimento de 5,0 cm e uma área de
seção transversal de 10,0 cm2. O material magnético
doce tem permeabilidade infinita. A bobina tem 100
espiras. A figura abaixo mostra a característica B-H
publicada pelo fabricante do ímã.
b) A área acima da curva de primeira imantação, no
1º. quadrante, multiplicada pelo volume do ímã fornece
a energia. A área hachureada fornece a densidade
volumétrica de energia, wv. Seu valor é de
aproximadamente 84 kJ/m3.
A energia é, pois,
W=w(Am)(lm)
3
W=84x10 (Am)(lm)=4.2 Joule
c) Se a resistência é desprezível, toda energia
armazenada no capacitor é transferida para o
sistema magnético, ou seja, para o ímã que requer
uma energia de 4.2 joules.
Conversão Eletromecânica de Energia – lista de exercícios sobre ímãs permanentes
4.2 =
1
C (vmax ) 2 ⇒ vmax = 290 Volts.
2
d) Pode ocorrer desmagnetização se a corrente
reversa (negativa), resultante do lugar geométrico B-H,
continuar além do joelho da curva, no 2º. quadrante. A
frequência da oscilação pode ser prevista,
aproximadamente, estimando-se a permeabilidade
saturada incremental a partir da parte mais alta da
característica (quase horizontal). Use esse valor para:
•
Verificar que a indutância saturada
incremental é de 0.5 mH.
•
Calcular a frequência de oscilação.
Figura 1(b) – Característica B-H do ímã permanente.
Inicialmente, uma armadura de material magnético
doce é inserida no entreferro de 0,5 cm de
comprimento. Em seguida, o ímã é magnetizado
através de uma bobina e passa a operar com sua
densidade de fluxo residual.
(a) Determine a densidade de fluxo no entreferro
quando a armadura é removida.
(b) O material do ímã permanente tem uma
permeabilidade de recuo de aproximadamente 2µ0.
Suponha que a armadura é reinserida no entreferro.
Calcule o novo valor da densidade de fluxo na região
ocupada pelo ímã.
Discussão
Ao invés de trabalhar com o campo H, o problema
pode ser resolvido de forma a determinar o fluxo
gerado pelo ímã φm (ou sua densidade Bm).
A reta de carga relaciona os valores de Bi e Hi
do ímã como parte daquele circuito magnético,
Figura – Ímãs para aplicações industriais
Questão
[adaptação, problema 2.35, Slemon]
No sistema magnético mostrado na Fig. 1(a) o material
do ímã permanente tem a característica B-H mostrada
na Fig. 1(b). Pode-se admitir que o material doce tem
permeabilidade infinita.
em particular. No caso, tem-se
Ag l i
Hi .
Ai l g
Bi = − µ0
(1)
A inclinação dessa reta depende somente da
geometria do circuito. Nesse problema, em particular,
das áreas e comprimentos do ímã e do entreferro.
A curva de desmagnetização publicada pelo
fabricante
é
completamente
genérica.
Relaciona B e H do ímã como parte de
qualquer circuito magnético. Às vezes inclui
até a curva de 1ª. imantação.
Com os valores numéricos, a reta de carga é
Bi = − µ0 (
36 6
)( )Hi = −18,0 µ0 .
24 0,5
(2)
Figura 1(a) – Sistema magnético com ímã permanente.
A partir da curva do fabricante é possível obter
a expressão de uma reta usando-se dois
pontos dessa curva. Por exemplo, (1,35 ; 0,00)
3
e (1,40 ; +20x10 ).
Bi =
(1,40 − 1,35)
((20x10 ) − 0)(H ) + 1,35.
3
i
(3)
os
Igualando-se os 2 membros das equações
(2) e (3) chega-se a
H i = −53,8kA / m; B = 1,215T .
(4)
Conversão Eletromecânica de Energia – lista de exercícios sobre ímãs permanentes
Pela continuidade do fluxo chega-se ao valor
entreferro se espalha por uma distância igual a g/2 de
desejado de Bg. Tem-se
cada uma das arestas do entreferro. Considere
também em seus cálculos um canal de fluxo que cruza
φímã = φgap .
a “janela” que separa as traves superior e inferior.
Bi Ai = Bg Ag
Bg =
ℜg =
4,0
Bi = 0,81T .
6,0
0,5 x10−2
µ0 (6,5)2 x10− 4
ℜcanal =
Slemon
Nossa
Bi = 1,120 T
Bi =1,215 T
a) Com a armadura reinserida, não se tem mais
entreferro, ou seja, o ímã está curto-circuitado e o
fluxo tende a aumentar. O ponto de operação
caminha pela reta de recuo a partir do ponto
(b = 1,215; h = −53.800)
6,0 x10 −2
µ0 (60 x10− 4 )
Figura – Ímãs para aplicações industriais
Questão
[adaptação, problema 2.40, Slemon
A figura 1(a) mostra a montagem de um retentor de
porta que utiliza um ímã permanente. A armadura
móvel deve ser fixada à porta, enquanto o restante da
montagem deve ser fixado à sua moldura. O ímã
usado é de cerâmica ferrite. A característica B-H,
idealizada, do ímã permanente é mostrada na figura
1(b). Pode-se admitir o ferro doce como tendo uma
permeabilidade infinita.
Ou seja, Bm passa de 1.215 T para um valor maior Bfinal
dado pela equação abaixo:
Bm = 1,215 + 2µ0 (53800)
Questão
Refaça os cálculos do problema anterior considerando
agora que o ímã utilizado é de Samário-Cobalto cujas
principais características são: Br=0,95 T e Hc=-720,00
kA/m.
Questão
[adaptação, problema 2.36, Slemon]
Nos problema anteriores, admitiu-se que todo o fluxo
gerado pelo ímã cruzava o entreferro. Em uma análise
mais elaborada, é possível incluir o efeito do
espalhamento que ocorre em torno das arestas do
entreferro. Mais ainda, deve-se considerar que de fato
existe fluxo magnético entre as traves horizontais
superior e inferior de material doce.
Suponha que inicialmente o ímã está operando com
sua densidade de fluxo residual de 1,35 T e que a
armadura está colocada no entreferro. Em seguida, a
armadura é removida.
(a) Deseja-se calcular o novo valor das densidades de
fluxo no ímã e no entreferro. Considere que o fluxo de
Figura 1(a) – Sistema magnético com ímã permanente.
Figura 1(b) – Característica B-H do ímã permanente.
Conversão Eletromecânica de Energia – lista de exercícios sobre ímãs permanentes
(a) A permeabilidade de recuo do material do ímã é
φ0 = B0 Am = (0,4)(4,0 x10 −4 ) = 1,6 E − 4 Wb.
1,15µ0. Mostre que a parte inclinada da característica
de desmagnetização pode ser usada como
l
característica de recuo para esse material.
ℜ0 =
= 1,73E 7 H/m
(b.1) Derive um circuito magnético linearizado para a
µ r µ 0 Am
montagem acima. Despreze o fluxo que atravessa a
janela entre as traves horizontais superior e inferior
x
ℜ g ( x) =
= (7,95 E 9) x
bem como o espalhamento no entreferro.
µ 0 Ag
(b.2) Determine o valor máximo do comprimento x do
entreferro para o qual esse circuito magnético é válido.
O circuito é válido até Bm = 0,15T .
xmax=1,81 mm.
(c) Em uma de suas formas possíveis, o circuito
φmin = 0,15 xAímã = 0,6 E − 4 Wb
magnético equivalente consiste de uma força
magnetomotriz constante em série com três relutores,
ℜ0
dois dos quais representam os entreferros. Derive uma
φ
=
φ0 Wb
min
expressão para a força que age sobre a armadura
ℜ
+
2
ℜ
0
g
móvel em função da distância x do entreferro. Qual o
valor dessa força quando x=1,0 mm ?
ℜ g máximo = 1,44 E 7 ∴
Resposta: fx=55,0 N.
(d) O modelo equivalente do item (b) prevê que o ímã
ℜ g máximo = 7,95 x10 9 ( x) = 1,44 x10 7
será desmagnetizado se o entreferro exceder um certo
comprimento. De fato, tal desmagnetização não ocorre
x = 1.81mm
por causa do fluxo de dispersão que atravessa o
“canal” que une as traves de ferro doce superior e
c. Circuito magnético: o ímã é representado por
inferior. Calcule a relutância desse canal e compare
uma força magnetomotriz em série com uma
com a relutância – supostamente máxima – que você
relutância R0.
calculou no item (b).
a. Inclinação
da
desmagnetização
µr =
característica
de
∆B 1
= 1,151
∆H µ 0
b. Circuito magnético: o ímã é representada
como fonte de fluxo, em paralelo com uma
relutância R0.
F0 = ℜ0φ0 = 2760 Ampères.
1 dℜ
fx = − φ 2
2
dx
2
d (ℜ0 + 2ℜ g )
1
F0
fx = −
2
2 (ℜ0 + 2ℜ g )
dx
fx = −
202
N; f x = −55 para x = 1,0mm
(1 + 919 x)2
d. Relutância do espaço de ar, entre as traves
superior e inferior
ℜcanal
1,0 x10−2
=
= 1,99 x107 H / m.
−4
µ0 ( 4,0 x10 )
O valor acima deve ser comparado com 2xRmax!
ℜmax =
Conversão Eletromecânica de Energia – lista de exercícios sobre ímãs permanentes
Na ilustração da Fig. 3 aparece o traçado das linhas
1,81x10−3
7
equipotenciais superpostas ao mapeamento colorido
= 4,525x10 H / m
−4
da densidade de fluxo B.
µ ( 2,0 x 0,5 x10 )
0
Figura – Ímãs para aplicações industriais
QUESTÃO
Um pequeno motor de corrente contínua, 2 polos, tem
seu campo criado por ímãs permanentes, com a
configuração mostrada na figura abaixo. Os detalhes
do enrolamento da armadura não estão incluídos na
figura. O comprimento axial do motor é 60 mm. A
densidade de fluxo requerida no entreferro é 0,3 tesla.
Figura 3 - Equipotenciais
• O ângulo α mostrado na Fig. 1 é 120º. Calcule
a relação entre o arco polar e o passo polar;
indique a extensão da zona neutra;
• Apresente um circuito magnético equivalente,
incluindo o efeito da dispersão; apresente um
breve comentário sobre esse circuito;
• Observe o traçado das equipotenciais e
identifique o fluxo útil e os fluxos dispersos.
• Mostre graficamente a interseção da
característica de desmagnetização do ímã
escolhido com a reta de carga do entreferro.
• Para inspecionar a distribuição do campo B no
entreferro, foi utilizado o contorno retilíneo
mostrado na Fig. 4. Os resultados mostram o
valor médio de B é aproximadamente 118 mT,
bem abaixo da especificação de projeto.
Figura - Vista transversal do motor cc
Na primeira análise foi usado um ímã cerâmico, o
“ceramic 5”, cuja característica B-H de 1º quadrante é
mostrada na Fig. 2.
Figura 4 – Contorno no entreferro
• Pode-se utilizar outro tipo de ímã para
contornar o problema do fluxo muito baixo
obtido na 1ª análise. Escolha um outro ímã e
calcule uma estimativa para a densidade de
fluxo B no entreferro. O quadro I mostra as
principais propriedades dos ímãs disponíveis
em nosso laboratório.
Figura 2 – Curva B-H do ímã ceramic 5
Conversão Eletromecânica de Energia – lista de exercícios sobre ímãs permanentes
Quadro I – Ímãs permanentes; dados comparativos
Liga
Fe89Nd7B4Na (Nano)
Ferrite
Alnico
SmCo5
SmCo17
Nd2Fe14B
Br (T) Hc (kA.m-1) (BH)max (kJ.m-3)
1,30
0,40
0,90
0,89
1,14
1,31
252
312
112
1.360
800
999
146
30
42
151
239
319