Lista_MU_MUV_3a_serie_2017

LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
1. (Espcex (Aman) 2017)
Um trem de 150 m de comprimento se desloca com
velocidade escalar constante de 16 m s. Esse trem atravessa um túnel e leva 50 s desde
a entrada até a saída completa de dentro dele. O comprimento do túnel é de:
a) 500 m
b) 650 m
c) 800 m
d) 950 m
e) 1.100 m
2. (Fatec 2017) A tabela apresenta dados extraídos diretamente de um texto divulgado
na internet pelo Comitê Organizador da Rio 2016, referente ao revezamento da Tocha
Olímpica em território brasileiro, por ocasião da realização dos XXXI Jogos Olímpicos
Modernos no Rio de Janeiro.
Revezamento da Tocha Olímpica
Duração
95
Percurso
Terrestre
dias
20.000 km
Total
Percurso Aéreo Total
Fonte
dos
dados:
10.000 milhas (  16.000 km)
<http://tinyurl.com/zf326a5>
Acesso em: 23.09.2016.
Dado: 1 dia  24 h
Utilizando como base apenas as informações fornecidas na tabela, podemos dizer que a
velocidade média da Tocha Olímpica ao longo de todo percurso é, em km h,
aproximadamente, igual a
a) 3,2  102
b) 1,6  101
c) 8,8  100
Página 1 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
d) 7,0  100
e) 4,4  100
3. (Pucrj 2017) Um carro saiu da posição xi  0 km e percorreu uma estrada retilínea e
horizontal até x f  10 km. Entre 0 km e 5 km, sua velocidade foi 60 km h e, entre 5 km e
10 km, sua velocidade foi 30 km h.
Calcule, em km h, a velocidade média para percorrer os 10 km totais.
a) 20
b) 30
c) 40
d) 45
e) 60
4. (Eear 2017) Uma aeronave F5 sai da base aérea de Santa Cruz às 16h30min para
fazer um sobrevoo sobre a Escola de Especialistas de Aeronáutica (EEAR), no
momento da formatura de seus alunos do Curso de Formação de Sargentos. Sabendo
que o avião deve passar sobre o evento exatamente às 16h36min e que a distância entre a
referida base aérea e a EEAR é de 155 km, qual a velocidade média, em km h, que a
aeronave deve desenvolver para chegar no horário previsto?
a) 1.550
Página 2 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
b) 930
c) 360
d) 180
5. (Eear 2017) Um garoto que se encontra em uma passarela de altura 20 metros,
localizada sobre uma estrada, observa um veículo com teto solar aproximando-se. Sua
intenção é abandonar uma bolinha de borracha para que ela caia dentro do carro, pelo
teto solar. Se o carro viaja na referida estrada com velocidade constante de 72 km h, a
que distância, em metros, do ponto diretamente abaixo da passarela sobre a estrada deve
estar o carro no momento em que o garoto abandonar a bola. Despreze a resistência do
ar e adote g  10 m s2 .
a) 10
b) 20
c) 30
d) 40
6. (Unesp 2016) Em uma viagem de carro com sua família, um garoto colocou em
prática o que havia aprendido nas aulas de física. Quando seu pai ultrapassou um
caminhão em um trecho reto da estrada, ele calculou a velocidade do caminhão
ultrapassado utilizando um cronômetro.
Página 3 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
O garoto acionou o cronômetro quando seu pai alinhou a frente do carro com a traseira
do caminhão e o desligou no instante em que a ultrapassagem terminou, com a traseira
do carro alinhada com a frente do caminhão, obtendo 8,5 s para o tempo de
ultrapassagem.
Em seguida, considerando a informação contida na figura e sabendo que o comprimento
do carro era 4m e que a velocidade do carro permaneceu constante e igual a 30 m / s,
ele calculou a velocidade média do caminhão, durante a ultrapassagem, obtendo
corretamente o valor
a) 24 m / s.
b) 21m / s.
c) 22 m / s.
d) 26 m / s.
e) 28 m / s.
7. (G1 - ifce 2016) A velocidade horizontal mínima necessária para uma pessoa pular
do ponto X e atingir o ponto Y, como mostra a figura abaixo, deve ser de
Página 4 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
(Despreze a resistência do ar e considere a aceleração da gravidade como sendo
g  10 m s2 )
a) 1m s.
b) 5 m s.
c) 4 m s.
d) 8 m s.
e) 9 m s.
8. (Efomm 2016) Uma balsa de 2,00 toneladas de massa, inicialmente em repouso,
transporta os carros A e B, de massas 800 kg e 900 kg, respectivamente. Partindo do
repouso e distantes 200 m inicialmente, os carros aceleram, um em direção ao outro, até
alcançarem uma velocidade constante de 20 m s em relação à balsa. Se as acelerações
são aA  7,00 m s2 e aB  5,00 m s2 , relativamente à balsa, a velocidade da balsa em
relação ao meio líquido, em m s, imediatamente antes dos veículos colidirem, é de
a) zero
b) 0,540
c) 0,980
d) 2,35
e) 2,80
Página 5 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
9. (Unicamp 2016) A demanda por trens de alta velocidade tem crescido em todo o
mundo. Uma preocupação importante no projeto desses trens é o conforto dos
passageiros durante a aceleração. Sendo assim, considere que, em uma viagem de trem
de alta velocidade, a aceleração experimentada pelos passageiros foi limitada a
amax  0,09g, onde g  10 m / s2 é a aceleração da gravidade. Se o trem acelera a partir
do repouso com aceleração constante igual a amax , a distância mínima percorrida pelo
trem para atingir uma velocidade de 1080 km / h corresponde a
a) 10 km.
b) 20 km.
c) 50 km.
d) 100 km.
10. (Efomm 2016) Um automóvel, partindo do repouso, pode acelerar a 2,0 m s2 e
desacelerar a 3,0 m s2 . O intervalo de tempo mínimo, em segundos, que ele leva para
percorrer uma distância de 375 m, retornando ao repouso, é de
a) 20
b) 25
c) 30
d) 40
e) 55
11. (Fmp 2016) Um jogador de futebol chuta uma bola sem provocar nela qualquer
efeito de rotação. A resistência do ar é praticamente desprezível, e a trajetória da bola é
uma parábola. Traça-se um sistema de eixos coordenados, com um eixo x horizontal e
paralelo ao chão do campo de futebol, e um eixo y vertical com sentido positivo para
cima.
Na Figura a seguir, o vetor v0 indica a velocidade com que a bola é lançada (velocidade
inicial logo após o chute).
Página 6 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Abaixo estão indicados quatro vetores w1, w2, w 3 e w4 , sendo w 4 o vetor nulo.
Os vetores que descrevem adequada e respectivamente a velocidade e a aceleração da
bola no ponto mais alto de sua trajetória são
a) w1 e w 4
b) w 4 e w 4
c) w1 e w 3
d) w1 e w 2
e) w 4 e w 3
12. (G1 - cps 2015)
Página 7 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Se hoje um filme pode ser armazenado na forma de um arquivo digital, no passado, ele
só podia existir na forma de rolos, contendo uma grande quantidade de fotogramas,
conforme figura. Para causar a impressão de continuidade, esses fotogramas eram
projetados um por um, a uma velocidade de 24 fotogramas por segundo.
Se a cada 30 mm da fita de um filme existe um único fotograma, em uma animação de
3
minutos de duração, a fita terá um comprimento aproximado, em metros, de
a) 70.
b) 90.
c) 130.
d) 150.
e) 220.
13. (Uece 2015) Um carro, partindo do repouso, desloca-se em um trecho A de modo
que sua velocidade aumente linearmente com o tempo até atingir 60km h. Após algum
tempo, em um trecho B, o motorista aciona o freio, de modo que a velocidade decresça
também linearmente com o tempo. Considere que a trajetória do automóvel é retilínea
nos dois trechos e que ambos sejam estradas sem aclives ou declives. Assim, pode-se
afirmar corretamente que o vetor aceleração nos dois trechos tem
a) mesma direção e mesmo sentido.
Página 8 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
b) mesma direção e sentido contrário.
c) mesmo módulo e mesmo sentido.
d) direções perpendiculares e mesmo módulo.
14. (G1 - ifsul 2015) Dois móveis, A e B, movendo-se em um plano horizontal,
percorrem trajetórias perpendiculares, seguindo os eixos Ox e Oy, de acordo com as
funções horárias x A  18  3t e yB  18  9t  2t 2, com unidades de acordo com o Sistema
Internacional de Unidades (S.I.).
Esses móveis irão se encontrar no instante
a) t  0,0s
b) t  3,0s
c) t  4,5s
d) t  6,0s
15. (Upf 2014) Dois móveis A e B deslocam-se em uma trajetória retilínea, com
acelerações constantes e positivas. Considerando que a velocidade inicial de A é menor
do que a de B (v A  vB ) e que a aceleração de A é maior do que a de B (aA  aB ),
analise os gráficos a seguir.
Página 9 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
O gráfico que melhor representa as características mencionadas é o:
a) A.
b) B.
c) C.
d) D.
e) E.
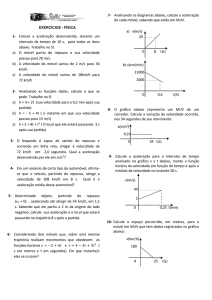
16. (Unesp 2013) Um garçom deve levar um copo com água apoiado em uma bandeja
plana e mantida na horizontal, sem deixar que o copo escorregue em relação à bandeja e
sem que a água transborde do copo.
O copo, com massa total de 0,4 kg, parte do repouso e descreve um movimento retilíneo
e acelerado em relação ao solo, em um plano horizontal e com aceleração constante.
Página 10 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Em um intervalo de tempo de 0,8 s, o garçom move o copo por uma distância de 1,6 m.
Desprezando a resistência do ar, o módulo da força de atrito devido à interação com a
bandeja, em newtons, que atua sobre o copo nesse intervalo de tempo é igual a
a) 2.
b) 3.
c) 5.
d) 1.
e) 4.
TEXTO PARA A PRÓXIMA QUESTÃO:
Um automóvel desloca-se por uma estrada retilínea plana e horizontal, com velocidade
constante de módulo v.
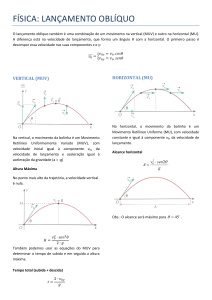
17. (Ufrgs 2013) Em certo momento, o automóvel alcança um longo caminhão. A
oportunidade de ultrapassagem surge e o automóvel é acelerado uniformemente até que
fique completamente à frente do caminhão. Nesse instante, o motorista "alivia o pé" e o
automóvel reduz a velocidade uniformemente até voltar à velocidade inicial v. A figura
abaixo apresenta cinco gráficos de distância (d)  tempo (t). Em cada um deles, está
assinalado o intervalo de tempo  Δt  em que houve variação de velocidade.
Escolha qual dos gráficos melhor reproduz a situação descrita acima.
Página 11 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
a)
b)
c)
d)
e)
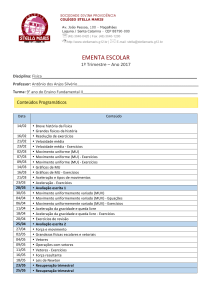
18. (Uespi 2012) Um motorista em seu automóvel deseja ir do ponto A ao ponto B de
uma grande cidade (ver figura). O triângulo ABC é retângulo, com os catetos AC e CB
de comprimentos 3 km e 4 km, respectivamente. O Departamento de Trânsito da cidade
informa que as respectivas velocidades médias nos trechos AB e ACB valem 15 km/h e
21 km/h. Nessa situação, podemos concluir que o motorista:
Página 12 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
a) chegará 20 min mais cedo se for pelo caminho direto AB.
b) chegará 10 min mais cedo se for pelo caminho direto AB.
c) gastará o mesmo tempo para ir pelo percurso AB ou pelo percurso ACB.
d) chegará 10 min mais cedo se for pelo caminho ACB.
e) chegará 20 min mais cedo se for pelo caminho ACB.
19. (Acafe 2012) Para garantir a segurança no trânsito, deve-se reduzir a velocidade de
um veículo em dias de chuva, senão vejamos: um veículo em uma pista reta, asfaltada e
seca, movendo-se com velocidade de módulo 36 km h 10 m s é freado e desloca-se
5,0 m até parar. Nas mesmas circunstâncias, só que com a pista molhada sob chuva,
necessita de 1,0 m a mais para parar.
Considerando a mesma situação (pista seca e molhada) e agora a velocidade do veículo
de módulo 108 km h  30 m s, a alternativa correta que indica a distância a mais para
parar, em metros, com a pista molhada em relação a pista seca é:
a) 6
b) 2
c) 1,5
d) 9
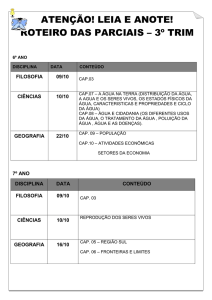
20. (Ufrgs 2012) A figura a seguir apresenta, em dois instantes, as velocidades v1 e v2
de um automóvel que, em um plano horizontal, se desloca numa pista circular.
Com base nos dados da figura, e sabendo-se que os módulos dessas velocidades são tais
que v1>v2 é correto afirmar que
Página 13 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
a) a componente centrípeta da aceleração é diferente de zero.
b) a componente tangencial da aceleração apresenta a mesma direção e o mesmo sentido
da velocidade.
c) o movimento do automóvel é circular uniforme.
d) o movimento do automóvel é uniformemente acelerado.
e) os vetores velocidade e aceleração são perpendiculares entre si.
Página 14 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Gabarito:
Resposta da questão 1: [B]
Situação 1: Trem iniciando a estrada ao túnel.
Situação 2: Trem finalizando a travessia do túnel.
O deslocamento total do trem durante a travessia foi tal que:
S  PP'  L  150
(1)
Como a velocidade do trem é constante, então:
v
S
 S  v  t
t
(2)
Substituindo-se a equação (1) na equação (2), tem-se que:
L  150  v  t  L  v  t  150
(3)
Substituindo-se os valores dos parâmetros conhecidos na equação (3), tem-se que:
L  v  t  150  16  50  150  800  150 
650 m
Resposta da questão 2: [B]
Página 15 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
A velocidade média é dada pela razão entre a distância total percorrida e o tempo total
gasto em percorrer essa distância:
vm 
Δs
Δt
Substituindo os valores e transformando as unidades para km h, temos:
vm 
 20000  16000  km
Δs
36000 km
 vm 
 vm 
24
h
Δt
2280 h
95 d 
1d
 vm  15,79 km h  vm
16 km h  1,6  101 km h
Resposta da questão 3: [C]
S  S0  V0  t  t 
ΔS
V0
5
1
 t1 
h  t1  5 min
60
12
5
1
t2 
 t 2  h  t 2  10 min
30
6
t1 
t t  t1  t 2  t t  5  10  t t  15 min  t t 
Vmédia 
1
h
4
10
 Vmédia  40 km h
1
4
Resposta da questão 4: [A]
1
h
10
ΔS
155
Vm 
 Vm 
 Vm  1.550 km h
1
Δt
10
6 min 
Resposta da questão 5: [D]
Δh 
1 2
gt
2
20  5t 2
t2  4
t  2 s
Página 16 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Como não existe tempo negativo, t  2 s.
S  S0  V0 t
ΔS  V0 t
ΔS  20 [m s]  2 [s]
ΔS  40 m
Resposta da questão 6: [D]
Dados: v A  30 m/s; Δt  8s; LA  4m; LB  30m.
Em relação ao caminhão, a velocidade do carro (vrel ) e o deslocamento relativo durante
a ultrapassagem (ΔSrel ), são:
vrel  v A  v C  v rel  30  v C .

ΔSrel  L A  LC  30  4  ΔSrel  34m.
v C  30  4 
 v rel 
ΔSrel
34
 30  v C 

Δt
8,5
v C  26m/s.
Resposta da questão 7: [B]
Para sabermos qual a velocidade mínima que ele deve exercer para realizar o salto,
primeiro precisamos saber quanto tempo que ele vai demorar pra descer em queda livre.
ΔS  V0y  Δt 
1
 a  Δt 2
2
1
 a  Δt 2
2
2ΔS
2  1,8
t
 t  0,6 s
a
10
ΔS  0 
t
Descobrimos que ele demora 0,6 s pra cair, logo ele deverá percorrer 3 m em 0,6 s. A
velocidade inicial que ele deve exercer será:
ΔS  V0x  Δt  V0x 
ΔS
3
 V0x 
 V0x  5 m s
Δt
0,6
Vale lembrar que a velocidade no eixo y sempre será um M.R.U.V. e a velocidade e no
eixo x sempre será um M.R.U.
Página 17 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Resposta da questão 8: [B]
Primeiramente, fazendo a conferência do tempo para atingir a velocidade terminal e a
distância percorrida por cada carro, temos:
Para o carro A:
Δt A 
Δv A
20m s
 Δt A 
 Δt A  2,8 s
aA
7m s2
ΔsA 
aA
7 m s2
2
2
  t A   ΔsA 
  2,8   ΔsA  28,6 m
2
2
Para o carro B:
ΔtB 
ΔvB
20 m / s
 ΔtB 
 ΔtB  4 s
aB
5 m s2
ΔsB 
aB
5 m s2
2
2
  tB   ΔsB 
  4   ΔsB  40 m
2
2
Como as distâncias percorridas somadas não ultrapassam o comprimento da balsa, os
dois móveis se chocam com a velocidade de 20 m s em relação à balsa e em sentidos
contrários.
Ao colidirem, temos a conservação da quantidade de movimento do sistema balsa e
carros, portanto:
Qf  Qi
Considerando como positivo o movimento do carro de maior massa e desprezando os
efeitos dos atritos, para o choque inelástico, temos:
mbalsa  mA  mB   v  mA  v A  mB  vB
v
mA  v A  mB  vB
800 kg  ( 20 m s)  900 kg  20 m s
v
 2000 kg  800 kg  900 kg 
mbalsa  mA  mB 
E, finalmente, a velocidade final da balsa será:
Página 18 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
v
18000  16000 kg  m s  v  0,54 m s no mesmo sentido do carro B.
3700 kg
Resposta da questão 9: [C]
Dados: a max  0,09 g  0,09 10   0,9 m/s2 ; v 0  0; v  1080 km/h  300 m/s.
A distância é mínima quando a aceleração escalar é máxima. Na equação de Torricelli:
v 2  v02  2 amax dmin  dmin 
v 2  v02 3002  02 90.000


 50.000 m 
2 amax
2  0,9
1,8
dmin  50 km.
Resposta da questão 10: [B]
Dividindo o movimento em duas partes, de acordo com o gráfico, temos:
As equações da velocidade para o trecho 1 e 2, são:
v1  2t1
v1  3  t 2  t1   v1  3t 2  3t1
Juntando as duas equações:
2t1  3t 2  3t1  t1 
3
t2
5
Logo, usando as equações para o cálculo da área dos triângulos juntos, temos o
deslocamento do móvel em todos os trechos:
Página 19 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Δs  Δs1  Δs2 
375 
t2  2 
2
t 2  v1
t  2t
 375  2 1
2
2
3
t
5 2  t 2  625  t  25 s
2
2
Resposta da questão 11: [D]
No lançamento oblíquo com ausência de atrito com o ar, podemos dividir o movimento
nos eixos vertical e horizontal, usando as componentes da velocidade nestes eixos
 v x e v y , conforme a figura abaixo:
Assim, temos no eixo vertical um movimento de lançamento vertical em que a
aceleração é dada pela gravidade local e no eixo horizontal um movimento retilíneo
uniforme em que a velocidade em x é sempre constante.
Observa-se que no ponto mais alto da trajetória a velocidade em y é nula e a velocidade
horizontal representa a velocidade da bola neste ponto, enquanto que a aceleração é a
mesma em todos os pontos do movimento, sendo constante e apontando para baixo.
Logo, a alternativa correta é letra [D].
Resposta da questão 12: [C]
Dados: f  24 Hz; Δt  3 min  180 s;  30 mm  0,03 m.
L  f Δ t  24  180  0,03  129,6 m 
L  130 m.
Resposta da questão 13: [B]
Página 20 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
No trecho A, o carro parte do repouso e aumenta sua velocidade uniformemente até
atingir a velocidade de 60km h.
Desta forma, a aceleração durante o trecho A tem direção como sendo a horizontal e
sentido da esquerda para a direita.
No trecho B, o carro está inicialmente com uma velocidade de 60km h e vai
desacelerando até atingir o repouso.
Assim, a aceleração no trecho B tem mesma direção que no sentido A (horizontal),
porém está no sentido contrário (da direita para a esquerda).
Resposta da questão 14: [D]
O encontro ocorrerá no ponto (0, 0), origem do sistema de eixos.
18

x A  18  3 t  0  18  3 t  t 
 t6 s

3


 y  18  9t  2t 2  0  18  9t  2t 2  t   9  81  144
B

4

t  1,5 s

t6s
t  6 s.
Resposta da questão 15: [D]
Página 21 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
Nota: há uma imprecisão gramatical no enunciado, afirmando (no singular) que os dois
móveis têm aceleração constante. É, então, de se supor que as acelerações sejam iguais.
Porém, logo a seguir, afirma-se que aA  aB . Para que se evitem confusões, o enunciado
na primeira linha deveria ser:
“Dois móveis A e B deslocam-se em uma trajetória retilínea, com acelerações
constantes e..."
Mas, vamos à resolução.
Como as acelerações (escalares) são constantes e positivas, os gráficos das velocidades
são trechos de reta ascendentes. Sendo aA  aB , o segmento referente à velocidade do
móvel A tem maior declividade, começando num ponto abaixo do de B, pois v A  vB .
Essas conclusões, levam-nos ao Gráfico D.
Resposta da questão 16: [A]
Dados: m = 0,4 kg; ΔS  1,6 m ; t = 0,8 s.
Calculando a aceleração escalar:
S 
2 S 2  1,6
a 2
3,2
t  a


 a  5 m /s2.
2
2
2
0,64
t
0,8
A força de atrito sobre o copo é a resultante. Aplicando o Princípio Fundamental da
Dinâmica para o movimento retilíneo:
Fat  m a  Fat  0,4  5  Fat  2 N.
Resposta da questão 17: [A]
[A] Verdadeira. Os gráficos apresentados são de deslocamento por tempo. Como o
enunciado nos informa que o automóvel desenvolve velocidade constante de módulo v,
no início e no final, teremos a função d  v.t de primeiro grau, ou seja, o gráfico deverá
ser uma reta no inicio e no final o que é satisfeito por todas as alternativas.
Página 22 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
No intervalo
Δt
o automóvel aumenta e em seguida diminui sua velocidade, ambos
uniformemente, o que nos remete à função d  v.t 
a.t 2
de segundo grau, ou seja, o
2
gráfico deverá ser duas parábolas seguidas, a primeira com concavidade para cima, o
que representa o aumento da velocidade e a segunda com a concavidade para baixo, o
que representa a diminuição da velocidade, sendo a alternativa [A] a única que satisfaz
o enunciado.
[B] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[C] Falsa. O gráfico apresenta uma reta no intervalo
Δt .
[D] Falsa. O gráfico apresenta uma reta no intervalo
Δt .
[E] Falsa. O gráfico apresenta, aparentemente, duas parábolas, porém com as
concavidades invertidas.
Resposta da questão 18: [C]
Dados: vAB = 15 km/h; vACB = 21 km/h.
Aplicando Pitágoras no triângulo dado:
| AB |2 | AC |2  | CB |2

| AB |2  9  16  25 
| AB | 5 km.
Calculando os tempos:

| AB | 5
1


h  Δt AB  20 min.
Δt AB 
v
15
3

AB

| AC |  | BC | 3  4 1
Δt


h  Δt ACB  20 min.
 ACB 
v ACB
21
3

 Δt ACB  Δt AB  20 min.
Resposta da questão 19: [D]
Calculando os módulos das desacelerações para pistas seca e molhada, com velocidade
inicial de 10 m/s e espaço de frenagem 5 m e 6 m:
Usando a equação de Torricelli:
Página 23 de 24
LISTA – MU/MUV – 3ª SÉRIE - TREINAMENTO
2
v 
v 02
pista seca: 02  102  2 a ΔS  2 a 5  100  a  10 m / s2 .
s
s
s
s

 2 a ΔS 
100
m / s2.
pista molhada: 02  102  2 am ΔSm  2 am 6  100  a s 
12

Calculando os espaços de frenagem para pistas seca e molhada, com velocidade inicial
de 30 m/s, com as respectivas desacelerações já calculadas.
Usando novamente a equação de Torricelli:
2
v 
v 02
pista seca: 02  302  2  10  ΔS  20 ΔS  900  ΔS  45 m.
s
s
s

 2 a ΔS 
100
100
2
2
ΔSm 
ΔSm  900  ΔSs  54 m.
pista molhada: 0  30  2 
12
6
m

Portanto, para a velocidade inicial de 30 m/s. em pista molhada ele percorre a mais:
ΔSm  ΔSs  54  45  9 m.
Resposta da questão 20: [A]
Todo movimento circular contém uma componente centrípeta voltada para o centro da
circunferência de módulo não nulo.
Página 24 de 24