Regressão Linear Simples 2010

Modelos de Regressão
Família de técnicas estatísticas vários fatores medidos (preditor,
covariável, variável independente) relacionados a um único desfecho
(variável resposta ou dependente).
Modelos de Regressão em Saúde
Supondo que se deseja analiar a relação:
custo x tipo tratamento análise de variância (média dos grupos)
Nível de dor (leve, moderada, severa) x tipo tratamento χ 2
Essa análise simples poderia induzir ao erro
Dor lombar
Rejane Sobrino Pinheiro
Tânia Zdenka Guillén de Torres
Tipo tratamento (mais vs
menos agressivo):
Medicação forte + repouso
prolongado
Retorno rápido atividade +
manejo dor com medicação
obtida em farmácia
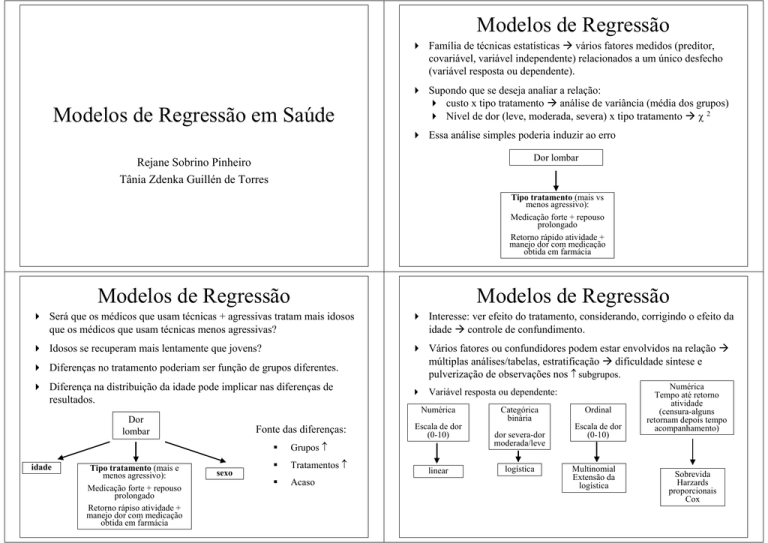
Modelos de Regressão
Modelos de Regressão
Será que os médicos que usam técnicas + agressivas tratam mais idosos
que os médicos que usam técnicas menos agressivas?
Interesse: ver efeito do tratamento, considerando, corrigindo o efeito da
idade controle de confundimento.
Idosos se recuperam mais lentamente que jovens?
Vários fatores ou confundidores podem estar envolvidos na relação múltiplas análises/tabelas, estratificação dificuldade síntese e
pulverização de observações nos ≠ subgrupos.
Diferenças no tratamento poderiam ser função de grupos diferentes.
Diferença na distribuição da idade pode implicar nas diferenças de
resultados.
Variável resposta ou dependente:
Numérica
Dor
lombar
idade
Tipo tratamento (mais e
menos agressivo):
Medicação forte + repouso
prolongado
Retorno rápiso atividade +
manejo dor com medicação
obtida em farmácia
Fonte das diferenças:
Grupos ≠
Tratamentos ≠
Acaso
sexo
Escala de dor
(0-10)
linear
Categórica
binária
dor severa-dor
moderada/leve
logística
Ordinal
Escala de dor
(0-10)
Multinomial
Extensão da
logística
Numérica
Tempo até retorno
atividade
(censura-alguns
retornam depois tempo
acompanhamento)
Sobrevida
Harzards
proporcionais
Cox
Modelos de Regressão
Modelos de Regressão
Conhecer efeito isolado de determinada variável:
Pode ser ferramenta poderosa para abordar 3 questões importantes:
predição, explicação (isolar efeito de um determinado preditor) e
entender comportamento de variáveis preditoras.
Moderada/grave-leve controlar pelos confundidores para conhecer
efeito isolado do tipo de tratamento
Predição:
Entendendo múltiplos preditores:
Quais pacientes com dor lombar terão limitação moderada/grave?
Identificar múltiplos preditores que independentemente influenciam o
resultado.
Categórica binária: moderada/grave vs leve idade, sexo, tipo
tratamento, tempo tratamento etc.
Necessário considerar complexidade como preditores influenciam
conjuntamente os resultados
Probabilidade de perfis de indivíduos terem moderada/grave limitação
de atividades
Numérica: custos idade, sexo, tipo tratamento, tempo tratamento.
Suponha que o efeito da dor lombar na limitação seja diferente para
diferentes grupos etários:
Para pacientes com dor leve/moderada, ser jovem prediz recuperação rápida
Para pacientes com dor severa, pouca diferença a idade faz.
Efeito de idade e nível de dor serão subrepresentados se a interação não
for levada em consideração.
O que é um modelo?
Nº de novos atendimentos de síndrome Distribuição do ácido úrico
de Down por mes
Modelos de Regressão freqüentemente usados
.4
0,4
.3
0,3
.2
0,2
.1
0,1
Regressão Linear
0
-4
-3
-2
-1
0
x
1
2
3
4
0
0
1
P( X = k ) =
2
3
4
1
f (x) =
σ 2π
k
( n−k )
n!
p (1− p)
k!(n − k )!
e
2
σ
(x − µ )
2
1
−
2
1.5
1
1
0.5
0.5
0
-0.5 0
10
15
20
25
-0.5 0
-1
-1
-1.5
-1.5
Análise de sobrevida (Modelos de Hazard
Proporcional)
0
5
Análise de Covariância
Regressão Logística
Modelos de Regressão
1.5
Análise de variância
5
10
15
20
25
Regressão de Poisson (Taxas de Incidência
baseadas em pessoa-tempo)
Modelos de Regressão segundo os tipos
de variável dependente e independente
Variável dependente
contínua
categórica
variáveis independentes
variáveis independentes
contínuas
categóricas
contínuas
+
categóricas
dependente do tempo
categóricas
ou
contínuas
não dependente do tempo
Regressão Linear
e/ou
Correlação
ANOVA
ANCOVA
Análise de Sobrevida
Regressão Logística
Análise de Regressão
Introdução
Análise de Regressão é uma técnica estatística para avaliar a relação de
uma ou mais variáveis independentes X1, X2, ..., Xk, com uma única
variável dependente contínua Y.
É uma análise apropriada para diferentes situações que podem se sobrepor:
1.
2.
3.
4.
5.
6.
Olhar a tendência – Caracterizar a relação entre a variável dependente Y e as
variáveis independentes X1, X2, ...,Xk olhando a direção, a extensão, e a
força da associação.
Ajuste de uma curva – Determinar o melhor modelo matemático (equação
ou fórmula matemática) que descreva a relação da variável dependente Y
como função das variáveis independentes X1, X2, ...,Xk.
Determinar qual ou quais variáveis independentes X1, X2, ...,Xk, são
importantes para descrever o comportamento da variável Y.
Fazer ajuste para controlar o efeito de variáveis de confundimento ou de
interação
Predição do comportamento de Y a partir das variáveis X1, X2, ...,Xk.
Obter curvas padronizadas para usar como referência (pediatria – alt x peso)
Regressão linear
Muitos fenômenos biológicos podem ser explicados por meio
de modelos matemáticos.
Em um experimento, é útil pensar as observações como
medidas compostas de um sinal e um ruído e construir
modelos matemáticos que incorporam ambos os
componentes. O sinal é considerado como o componente
determinístico e o ruído é o componente aleatório.
Assim, um modelo matemático de dados que combina sinal
e ruído é probabilístico e é chamado de modelo estatístico.
Outra maneira de pensar um modelo estatístico é considerar o
sinal como a descrição matemática das principais
características dos dados e o ruído como todas as
características não explicadas pelo modelo, isto é, pelo seu
componente determinístico.
O problema
Dada uma amostra de n indivíduos, foi observado para cada um
os valores das variáveis X (explicativa) e Y (dependente).
Temos, então, n pares de observações (X1, Y1), (X2 Y2), ..., (Xn,
Yn), onde os subscritos referem-se a cada indivíduo.
Cada par de valores pode ser representado em um espaço
bidimensional, em um gráfico denominado diagrama de
espalhamento ou de dispersão (scatter plot).
A figura ilustra uma relação quase perfeitamente linear entre nº.
de cigarros por dia e Ca. de laringe.
A linha que representa os pontos é uma reta de regressão,
significando que ela estima os valores médios para a variável Y
(escala vertical) de acordo com valores da variável X (nas
abscissas).
Raramente os dados em pesquisas epidemiológicas seguem um
padrão tão evidente.
Neste caso, é uma regressão simples, porque pode ser descrita por
uma única variável independente, cuja equação é:
Y = α + βX + ε.
α → intercepto (valor de Y quando X = 0).
β → coeficiente de X e descreve a inclinação da reta → representa a
quantidade de aumento médio em Y para um aumento de 1
unidade de X.
ε componente de ruído
Supondo que todos os confundimentos e vieses tenham sido
administrados apropriadamente, a inclinação 0,282 quantifica o
efeito do cigarro na morte por Ca. de laringe. A reta de regressão
também nos permite estimar as razões de taxas de mortalidade
para diferentes níveis de fumo.
Exemplo:
a taxa de mortalidade pode ser estimada para 50 cigarros por dia
(equivalente a 2,5 maços por dia) → 15,2. Comparado com a
taxa estimada entre os não fumantes de 1,15, a razão de taxas
para os que fumam 2,5 maços por dia é 15,2 / 1,15 = 13,1.
O coeficiente de regressão indica um forte efeito do fumo na
mortalidade por Ca. de laringe.
Na figura, Y é a taxa de mortalidade padronizada por idade
para Ca. de laringe e X é o N°. de cigarros fumados por dia. A
equação para a reta de regressão da figura é :
Y = 1,15 + 0,282 X.
Estes valores (Y) referem-se a mortes por 10000 pessoas-ano.
O intercepto (1,15) representa o N°. de mortes por 10000
pessoas-ano que são estimadas ocorrerem na ausência de fumo.
Existe uma observação direta para taxa para o nível 0 de fumo,
que é 0,6 mortes por 10000 pessoas-ano. A reta de regressão
estimou um valor um pouco maior (1,15) do que é observado.
Esta estimativa é baseada não somente no ponto relativo a um
não fumante, mas nos 5 pontos do conjunto.
A inclinação da reta de regressão de 0,282 indica que o nº. de
mortes por 10000 pessoas-ano é estimado aumentar em 0,282 a
cada cigarro a mais fumado diariamente.
Outro exemplo: Idade e pressão arterial sistólica
(PAS) de 30 indivíduos.
A PAS "depende" da idade do indivíduo.
Duas questões básicas devem ser consideradas em qualquer
análise de regressão:
Qual é o modelo matemático mais apropriado a ser
utilizado → linha reta, parábola, função log etc.?
Dado um modelo específico, como será determinado o
melhor ajuste do modelo aos dados? Ou seja, se o modelo
for uma reta, como encontraremos a melhor reta que se
ajusta aos pontos?
PAS x idade
O gráfico, chamado de diagrama de dispersão, ajuda a entender
a relação.
O gráfico mostra que os dados se distribuem em torno de uma
linha reta. Podemos encontrar qual a reta que melhor se adequa
aos dados e descrever sua equação, que seria o modelo para os
dados.
PAS x idade
180
Este método chama-se de ajustar uma regressão linear simples
ao conjunto de dados.
180
PAS (mmHg)
PAS (mmHg)
Podemos dizer que a PAS é a variável dependente e a idade é
a variável independente.
160
140
120
100
160
140
120
100
10
30
50
70
10
idade (anos)
30
50
70
idade (anos)
Se a reta ajustada captar bem o padrão dos dados, poderemos
tê-la como o modelo da relação entre PAS e idade.
Podemos, então, predizer diferentes valores de PAS para
diferentes idades.
Ajuste de uma regressão linear simples
Equação da reta:
Qual é a melhor reta que descreve a relação?
Se os pontos estivessem alinhados, não haveria dúvidas quanto
à melhor reta.
Na prática, temos uma nuvem de pontos, onde caberiam uma
infinidade de retas.
Como a reta será ajustada usando os dados de uma amostra e
não de toda a população, temos que nos haver com a questão
estatística de estimação de parâmetros. Quais são eles?
Equação da reta:
Y=α+βX
Y=α+βX
Se Y é uma variável aleatória, pode-se descrever Y em
função de X , por meio de um modelo, onde α e β são
parâmetros e ε é o erro aleatório.
Y=α+βX+ε
Erro aleatório é a distância ou diferença entre o valor
observado (resposta) para o indivíduo e o valor obtido pela
reta de regressão
Os valores αˆ e βˆ
ou ( a e b ) são estimadores dos
parâmetros α e β da reta.
Regressão Linear Simples
yi =
+ β x1
+
1 43
14424
α
comp. det er min ística
ε{i
,
ε i ~ N (0,σ
y = 2x+1
2
13
)
y
11
comp.aleatória
9
y i = 514+44224* x4143
7
25 unid
comp. det er min ística
3
1
-3
-2
-1 0
-1
1
-3
2
3
4
5
1 unid
x
Taxa/variação a cada aumento de 1 unidade em x,
tenho variação de β unidades em y.
Propriedades Matemáticas da Reta
Coeficiente angular inclinação
y 20
y = f(x) = -2x + 1
15
y = f(x) = -x + 1
10
y = f(x) = 0,5x + 1
5
y = f(x) = x + 1
y = f(x) = 2x + 1
y = f(x) = 3x + 1
0
-3
-1
-5
1
3
6
5
x
-10
-15
Quanto maior o valor de β maior a inclinaçãoda reta
Pressupostos básicos
Coef. Linear/deslocamento/intercepto:
y = f(x) = x - 2
y = f(x) = x - 1
y = f(x) = x
y = f(x) = x + 0,5
y = f(x) = x + 1
y = f(x) = x + 2
Para o ajuste de uma regressão linear simples a um conjunto de
dados é necessário fazer algumas pressuposições.
y8
6
4
2
0
-4
-2
-2 0
-4
2
4
6
x
-6
A (inclinação) é a mesma.
Quanto maior o coeficiente linear (α
α), maior é o
deslocamento vertical (intercepto / patamar inicial) em y.
1. A relação entre as duas variáveis é linear
• Só deve ser usada a reta para descrever um fenômeno se, no
intervalo estudado, a relação entre as duas variáveis puder ser
expressa por uma reta.
• Para estabelecer o modelo que descreve o fenômeno, existem
2 procedimentos alternativos: ou existe uma teoria que
fornece a equação ou "procura-se" a equação, olhando os
dados (ou gráfico).
• Não existe um modelo teórico que explique como a PAS
aumenta com a idade. A relação linear parece perfeitamente
aceitável.
2. Os valores de X são fixos, isto é, não é variável aleatória
Pressupostos básicos (cont...)
3. A variabilidade de Y, para qualquer valor dado de X, é sempre a
mesma homocedasticidade.
Para cada valor de X teremos uma distribuição de valores de Y
Quantidade de procaína
hidrolisada (moles/l) no plasma
sangüíneo em determinados
instantes de tempo
Tempo de corrida (s) em
função do percurso em metros
variância crescente
Pressupostos básicos (cont...)
4. O erro de uma observação não está correlacionado com o erro de
outra observação.
•
•
Ou seja, as observações são independentes
Mais de uma observação de um mesmo indivíduo dependência
5. Para qualquer dado valor de X, os valores de Y têm distribuição
normal.
•
^
Os desvios ( Yi − Yi ) têm distribuição normal
6. As observações representam uma amostra aleatória
Determinando a reta de melhor ajuste
Métodos de Estimação dos parâmetros
Estimativas dos parâmetros
O método mais simples é ajustar "no olho", porém é extremamente
subjetivo e impreciso. Existem soluções analíticas para o ajuste.
Método dos mínimos quadrados
A melhor reta é a que minimiza a soma dos quadrados das distâncias
verticais (diag. espalhamento) entre a observação e a reta ajustada.
Método de Mínimos Quadrados
Escolhe a e b de modo a minimisar a soma dos quadrados das
diferenças entre o valor observado e o valor estimado pela reta
Y = a + bX
As distâncias verticais correspondem à diferença entre o valor
observado para Y e o valor estimado, segundo o modelo da reta.
A distância vertical entre o ponto observado (Yi) e o ponto
correspondente (ao valor de Xi) na reta de regressão ( Yˆ i ) é chamado
de erro εi, e é dado por:
Matematicamente, o método dos mínimos quadrados é descrito
como a seguir:
ˆ
Yˆi = αˆ + β X i
ε
^
^
^
= Yi − Yi = Yi − (α + β X i )
i
estimativa da resposta (Y) para o valor Xi, baseado
no modelo, ou seja, na reta de regressão.
Na reta de regressão, ou modelo:
αˆ e βˆ
(Xi, Yi)
são o intercepto e a inclinação da reta ajustada.
ponto observado
A soma dos quadrados dos erros ou resíduos (distâncias entre o
observado e o estimado) é dado por:
n
^
n
^
^
SSE = ∑(Yi −Yi )2 = ∑(Yi −α− β Xi )2
i=1
Solução para o problema do melhor ajuste
Dados:
: a média dos valores observados da variável dependente Y
Y
: a média dos valores observados da variável independente X
X
i=1
A solução via o método dos mínimos quadrados é a escolha de αˆ e βˆ
para os quais a soma dos quadrados descritos acima seja mínima.
n
^
β=
_
^
n
_
_
i=1
2
i
A equação da reta pode ser generalizada como:
ˆ
Yˆi = αˆ + β xi
^ _
α = Y− β X
i=1
∑(X − X)
No jargão estatístico, αˆ e βˆ são ditos estimadores de mínimos
quadrados para os parâmetros α e β da população.
O valor mínimo da soma dos quadrados dos erros SSE → é uma
medida de grande importância para avaliação da qualidade do ajuste
da reta.
_
∑(Xi − X)(Yi −Y)
_
_
Yˆ = Y+ βˆ(X − X )
Utilizando os dados da tabela de PAS e idade, podemos calcular a
reta que melhor se ajusta aos dados, ou seja a reta estimada.
A força da relação entre duas variáveis (uma resposta e uma
variável independente) é medida pela inclinação ou β.
^
Y = 98,71+ 0,97X
Existe um ponto distoante, cuja
retirada deve ser bem avaliada.
Retirando o ponto distoante:
^
Y = 98,08+ 0,95X
PAS x idade
PAS (mmHg)
Inferência sobre a inclinação da reta (β) e sobre o intercepto (α)
240
220
200
180
160
140
120
100
Para avaliar se a reta ajustada auxilia na predição de Y a partir de X,
e para levar em consideração as incertezas devidas a estar-se
utilizando um conjunto de observações (amostra) para estimarmos a
reta → é uma prática padrão calcularmos o intervalo de confiança ou
o teste estatístico de hipóteses sobre os parâmetros desconhecidos do
modelo linear proposto (população).
Considerando que Y tenha distribuição normal, α e β também terão
distribuição normal.
10
30
50
70
idade (anos)
♦ Se há relação de X e Y, então β é diferente de zero.
♦ O teste T testa a hipótese alternativa H1 de que a inclinação β é
significativamente diferente de zero.
H1 : β ≠ 0
♦ A hipótese mais conservadora é de que a inclinação seja zero,
ou seja, não há associação entre X e Y,
H0: β = 0:
♦ A estatística do teste é definida como:
^
0 ^
β − µβ
β
T=
=
SE ^
SE ^
β
β
♦ Similarmente, para o intercepto,
H0: α^= 0 vs H1: α ≠ 0 :
^
T=
α − µα
SE ^
α
=
α
SE ^
α
♦ O teste T utiliza n - 2 graus de liberdade, pois envolve S2, que possui
n - 2 graus de liberdade e é o único componente randômico no
denominador.
♦
Testando a hipótese, a um nível de significância α, rejeita-se H0
quando:
|T| ≥ tn-2,1-α/2 para um teste bilateral →
H1: β ≠ 0 ou H1: α ≠ 0
♦ Onde tn-2,1-α/2 é o percentil 100(1-α/2)% da distribuição t com n-2
graus de liberdade
♦ Podemos, alternativamente, calcular os p valores baseados no cálculo
da estatística T → resultado de pacotes computacionais.
H0 : β = 0
H1 : β ≠ 0
Interpretação do teste para inclinação e intercepto
^
T=
β
Teste para inclinação zero → Ho: β = 0.
SE ^
β
Grande chance de
acontecer pelo acaso
α/2
α/2
Região de rejeição de Ho
Pouca chance de
acontecer pelo acaso
Região de rejeição de Ho
Região de “não rejeição” de Ho
Pouca chance de
acontecer pelo acaso
Se H0: β = 0 NÃO é rejeitada → a inclinação é zero (ou melhor, não é
significativamente diferente de zero); duas interpretações são possíveis:
Supondo que o modelo seja linear, X não ajuda a predizer Y
(não há relação de X e Y).
Há uma relação entre X e Y (X ajuda a predizer Y), porém esta
relação não segue uma reta. O fato da reta ajustada ser zero não
significa necessariamente que não exista relação entre X e Y. O
modelo linear pode não ser apropriado.
Teste para intercepto zero
♦Ho: α = 0
♦É uma hipótese de menor interesse.
Se H0: β = 0 é rejeitada → a inclinação é diferente de zero, duas
interpretações são possíveis:
X ajuda e muito a predizer Y. Há relação entre X e Y.
Pode ser que exista um modelo melhor, por exemplo, um
curvilíneo. Porém, há um componente linear que não deve ser
desprezado e deve ser incluído no modelo final.
♦ Combinando as interpretações acima, pode-se dizer que um modelo que
inclua a variável X é melhor do que um modelo que não inclua, porém não
necessariamente o modelo deverá incluir X somente como uma
componente linear.
♦De um modo geral, não possui correspondência com a realidade
(idade = 0, PAS = 0).
♦Caso a hipótese NÃO seja rejeitada (α = 0) pode ser apropriado
remover a constante do modelo discutível.
♦Remover induz a que o modelo passe no ponto (0,0) saber se
faz sentido.
Inferência sobre a reta de regressão - Intervalo de
confiança para a reta de regressão
Como a reta foi obtida a partir de uma amostra de pontos, ela será a
estimativa pontual da relação das variáveis na população.
Pode ser do interesse considerar a incerteza desta estimativa, com o
cálculo do intervalo de confiança para a reta de regressão propriamente
dita.
O IC de 95% da reta de regressão quer dizer que, para as possíveis
amostras de pontos, 95% dos intervalos calculados conterão a
verdadeira reta de regressão.
Ou seja, para um determinado valor de X = X0, pode-se querer calcular
o intervalo de confiança para o resultado estimado, ou seja, para o
valor médio de Y dado o valor X0.
^
Y X 0 ± t n−2,1−α / 2 S ^
YX 0
Intervalo de confiança para a reta de regressão
A forma mais conveniente de se representar o IC da reta é calcular os
limites superior e inferior de Y para diferentes valores de X, e
representar no mesmo gráfico dos limites de confiança para a reta de
regressão.
_
i = 0,1,2,.. . e usar um valor de k que
Por exemplo, usar X 0 = X ± ik ,
permita que o intervalo de dados de X seja coberto uniformemente.
Intervalo de confiança para a reta de regressão
^
Dados:
: a média dos valores observados da variável dependente Y
Y
: a média dos valores observados da variável independente X
X
Para um determinado X = X0, o valor estimado de Y ( YX ) corresponde
ao valor médio de Y para X0.
0
^
T=
YX 0 − µ Y |X 0
S
^
YX 0
^
n
^
_
∑(X − X)(Y −Y)
β = i=1
i
i
n
_
^
_
α = Y− β X
_
_
^
Valor predito de Y para X0
_
S
2
^
YX 0
i
= SY | X
1 ( X 0 − X )2
+
n (n − 1) S X2
^
estimativa do erro padrão de YX
0
^
Interpretação + “real”
centrando X na média A equação da reta pode ser generalizada como: PAS para as pessoas
com idade
ˆ
Yˆi = αˆ + β xi
^
^ _
∑(X − X)
i=1
^
YX 0 = α + β X 0 = Y + β ( X 0 − X )
_
Substituindo α
_
_
Yˆ = Y+ βˆ (X − X )
Para o cálculo do intervalo de confiança para α e β.
O IC de 100(1-α)% de confiança é dado por:
Y X 0 ± t n−2,1−α / 2 S
^
intervalo de confiança para X = X0
YX 0
Para o cálculo do intervalo de confiança de 90%, para os dados de PAS e idade, a fórmula
fica simplificada para:
142.53 + (0.97)( X 0 − 45.13) ± 29.45 0.033 +
( X 0 − 45.13) 2
6783.48
Dif. aumenta nas bordas
Medindo a qualidade do ajuste
♦Uma vez que a reta dos mínimos quadrados é obtida, é de
interesse saber se esta reta ajustada consegue predizer Y e, em
conseguindo, em que medida.
♦A medida que auxilia na resposta a esta questão é o SSE (soma
dos quadrados dos erros ou soma dos quadrados dos resíduos)
n
IC da reta - média
SSE =
∑
^
(Yi − Yi ) 2
i =1
“fx ref.” para indivíduos
♦Se SSE = 0, a reta está perfeitamente ajustada aos pontos, ou seja,
^
Yi = Yi para cada i (observação). Cada ponto cai exatamente sobre a
reta de regressão.
♦À medida que o ajuste fica pior, SSE aumenta, uma vez que os
desvios entre os pontos observados e a reta ficam grandes.
Coeficiente de Correlação e a Análise de Regressão Linear
O coeficiente de correlação amostral r é definido como:
♦É uma estatística bastante utilizada que fornece uma medida da
relação linear entre duas variáveis.
SSXY
r XY
♦Possui propriedades semelhantes às da regressão linear.
♦O coeficiente de correlação entre Y e X é o mesmo que o
coeficiente de correlação entre X e Y, para o mesmo conjunto de
observações.
♦Existem vários tipos de coeficientes de correlação (Pearson,
Spearman, phi, etc.). Depende do tipo de variável.
♦O usado com maior freqüência é o coeficiente de correlação de
Pearson. Ele é denotado por ρXY (ρ
ρ = rho) quando calculado a partir
de uma população de observações X, Y, e por rXY quando calculado a
partir de uma amostra de observações X,Y. rXY é um estimador de
ρXY.
Propriedades do Coeficiente de Correlação
♦É um índice sem unidades de medida - adimensional.
♦Varia entre –1 e 1
[-1 ≤ rXY ≤ 1]
♦Uma correlação igual a 0 significa falta de relação linear entre X e Y.
♦Uma correlação positiva indica que X e Y estão relacionadas
diretamente, quer dizer que as duas medidas tendem a crescer ou
decrescer juntas
♦Uma correlação negativa indica que X e Y estão relacionadas
inversamente, quer dizer que, à medida que uma variável cresce, a outra
tende a decrescer
♦r = 1 ou r = -1 indicam uma relação linear perfeita entre X e Y
♦De certo modo, é uma medida do grau de dispersão dos pontos em torno
de uma reta: quanto maior a dispersão, menor r
=
(
∑ (X i − X )(Y i − Y )
) (
2
∑ X i − X ∑ Y i −Y
)
2
=
SSXY
SSX .SSY
SSY
SSX
A fórmula equivalente para r, que o relaciona com a inclinação da
reta de regressão é dada por:
n
^
_
_
∑ ( X i − X )(Yi − Y )
β = i =1
n
_
∑ ( X i − X )2
SSXY
=
SSXY
SSX
i =1
1
^
SSX 1
SSX
( SSX .SSY ) 2
2 = SX ⇒ r = β SX
=
=
=
1
1
^
1
SSXY
SY
SY
SSY
2
SSX 2 .SSY 2
β
SSX
r