O tamanho da Terra

Mecânica
Gabarito comentado
1.
O tamanho da Terra
Há 4,5 bilhões de anos (idade estimada do planeta em que vivemos e quando sequer existia o
homem – que a ciência supõe haver surgido há apenas 100 milhões de anos), a Terra perfaz uma
volta inteira ao redor do Sol em exatas 23 horas, 56 minutos e 38 segundos. É o chamado dia,
ou período de rotação terrestre. É oportuno informar que a Terra gira ao redor do Sol a 107.244
quilômetros por hora.
Sabedores da existência dos três principais parâmetros de latitude da Terra (Equador e os
Trópicos de Câncer e de Capricórnio), os antigos gregos tiveram condições de determinar a
dimensão do nosso planeta. O primeiro a calcular o tamanho da Terra foi o geômetra grego
Eratóstenes de Cirene (276 a 196 antes de Cristo). Ele chegou ao valor de 46.000 quilômetros
para a circunferência da Terra que passa pelos pólos Norte e Sul. Feito extraordinário, já que
medidas atuais e de altíssima precisão fixam em 40.000 quilômetros a circunferência polar.
(Revista Na Poltrona, ano 6, no 71, maio de 2005.)
Um relâmpago é uma corrente elétrica muito intensa que ocorre na atmosfera com típica duração
de meio segundo e típica trajetória com comprimento de 5 a 10 quilômetros. Ele é conseqüência
do rápido movimento de elétrons de um lugar para outro. As cargas no canal movem-se rumo ao
solo em etapas com uma velocidade média de cerca de 100 km/s. A carga negativa média
transferida ao solo é de cerca de 10 coulombs, com valores máximos em torno de 200 coulombs.
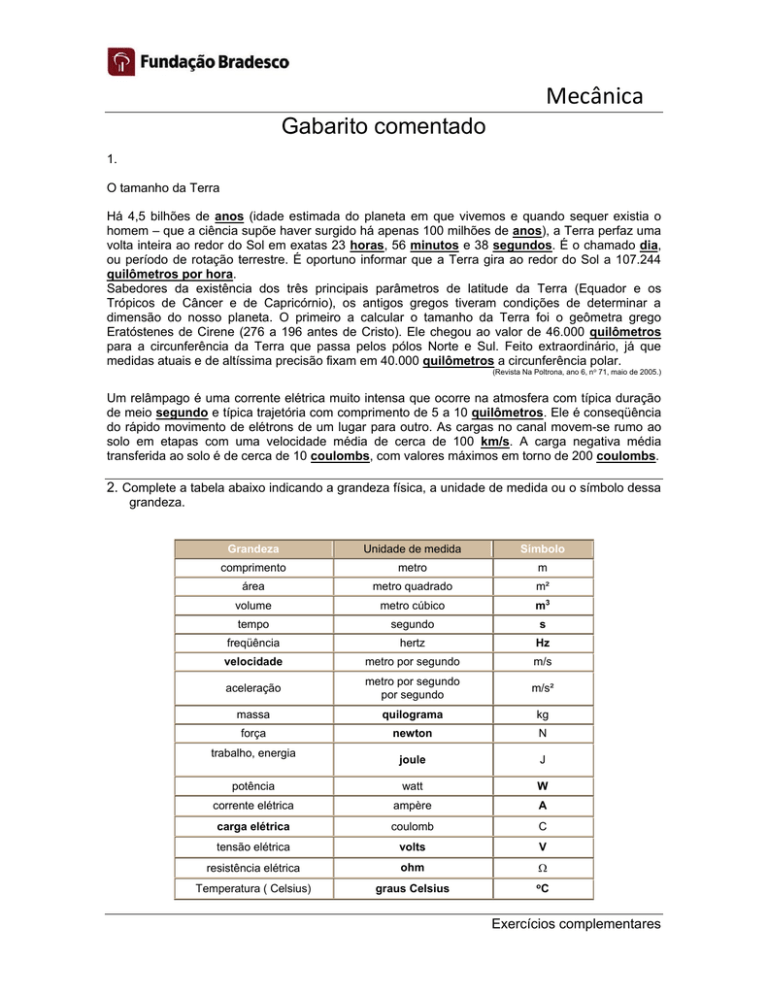
2. Complete a tabela abaixo indicando a grandeza física, a unidade de medida ou o símbolo dessa
grandeza.
Grandeza
Unidade de medida
Símbolo
comprimento
metro
m
área
metro quadrado
m²
volume
metro cúbico
m3
tempo
segundo
s
freqüência
hertz
Hz
velocidade
metro por segundo
m/s
aceleração
metro por segundo
por segundo
m/s²
massa
quilograma
kg
força
newton
N
joule
J
potência
watt
W
corrente elétrica
ampère
A
carga elétrica
coulomb
C
tensão elétrica
volts
V
resistência elétrica
ohm

Temperatura ( Celsius)
graus Celsius
oC
trabalho, energia
Exercícios complementares
Mecânica
3.
A
S
D
F
G
H
O
T
N
E
M
O
M
P
O
I
U
Y
Y
Q
F
O
R
Ç
A
T
C
P
Q
E
E
R
T
Y
U
I
O
P
P
U
E
R
I
C
O
R
R
E
N
T
E
E
L
E
T
R
I
C
A
A
F
U
N
D
B
R
A
S
C
H
E
F
I
N
H
A
C
R
I
N
ççç
A
R
Z
X
C
V
B
O
T
R
A
B
A
L
H
O
F
I
S
T
P
V
E
B
H
B
H
T
E
M
P
E
R
A
T
U
R
A
E
I
N
O
T
S
B
O
L
H
O
F
R
E
Q
U
E
N
C
I
A
D
P
C
E
I
I
C
O
L
L
I
N
S
A
S
S
A
M
S
S
A
O
T
Y
U
I
S
P
E
R
I
O
D
O
F
F
G
H
J
D
T
M
N
B
V
C
T
E
V
E
L
O
C
I
D
A
D
E
E
E
E
A
M
C
A
B
C
E
Q
A
Z
E
D
C
R
F
V
S
X
D
N
P
O
X
A
P
A
X
N
I
R
E
C
U
I
S
P
I
M
E
C
A
L
O
R
M
B
G
H
C
F
P
S
Q
U
O
A
M
R
M
I
L
D
N
U
N
P
V
T
G
I
Q
O
L
K
T
D
P
V
O
A
O
E
A
N
A
K
O
I
N
N
A
Y
O
D
N
A
U
A
V
R
D
N
C
P
O
M
U
M
S
Ç
O
B
I
A
E
K
L
N
I
A
M
S
I
G
D
A
L
A
A
S
P
O
C
K
M
C
S
H
M
A
K
I
R
K
C
M
T
R
O
G
U
H
U
R
I
A
O
A
E
I
M
D
C
C
O
Y
E
B
A
N
N
B
A
N
R
F
L
I
N
G
J
A
C
B
D
L
P
V
N
R
T
E
E
L
P
M
M
T
T
R
J
D
M
G
E
M
P
U
X
O
P
I
T
X
M
B
A
E
O
E
A
E
V
C
Z
E
D
A
C
I
S
I
F
I
O
C
V
M
F
N
D
B
A
O
V
O
P
R
E
S
S
A
O
S
C
G
T
P
I
E
E
C
A
R
G
A
E
L
E
T
R
I
C
A
T
O
A
O
A
Exercícios complementares
Mecânica
4. Teremos os valores apresentados na tabela:
v
t
VECTRA
100 – 0 = 100 km/h = 27,8 m/s
6,5 s
FORD RANGER
100 – 0 = 100 km/h = 27,8 m/s
12,5 s
a = 27,8 = 4,3 m/s2
6,5
a = 27,8 = 2,2 m/s2
12,5
BMW 645
100 – 0 = 100 km/h = 27,8 m/s
7,1 s
a = 27,8 = 3,9 m/s2
7,1
PORSCHE
200 – 0 = 200 km/h = 55,6 m/s
10 s
a = 55,6 = 5,6 m/s2
10
Carro
a = v
t
O Porsche possui maior aceleração. O Ford Ranger possui a menor aceleração.
5. Nas situações mostradas as forças são perpendiculares. Nesse caso utilizamos o Teorema de
Pitágoras para determinar a força resultante.
Norte
a) Fr2 = (6)2 + (8)2
Fr2 = 36 + 64
Fr2 = 100
Fr = 10 N
6N
Oeste
Leste
Sul
Força resultante
Valor: 10 N
Direção: leste-oeste
Sentido: de oeste para leste
8N
b) ) Fr2 = (3)2 + (4)2
Fr2 = 9 + 16
Fr2 = 25
Fr = 5 N
Valor: 5 N
Direção: norte-sul
Sentido: de norte para sul
4N
3N
Força resultante
Exercícios complementares
2
2
c) Fr = (9) + (12)
Fr2 =81 + 144
Fr2 = 225
Fr = 15 N
12 N
2
Valor: 15 N
Direção: leste-oeste
Sentido: de leste para oeste
Mecânica
Força resultante
9N
6.
O corpo 1 possui velocidade crescente. Encontra-se em movimento retilíneo uniformemente
acelerado.
O corpo 2 possui velocidade decrescente. Encontra-se em movimento desacelerado.
O gráfico do corpo 3 mostra que sua velocidade permanece constante. Encontra-se em movimento
retilíneo uniforme.
7. Utilizando a expressão
 = F.d
onde F = 800 N e
d = 1,5 – 1,0 = 0,5 m
 = F.d
 =800.0,5
 = 400 J
8. Utilizando a expressão:
Ep = m.g.h
onde
m = 90 kg
g = 10 m/s2
h = 800 m
Teremos:
Ep = m.g.h
Ep = 90.10.800
Ep = 720.000 J
Para a energia cinética
Ec = m.v2
2
Ec = 90.(11)2
2
Ec = 90.121
2
Ec= 5.445 J
E para a energia mecânica
Exercícios complementares
Mecânica
Emecânica = Ec+ Ep
Emecânica = 5.445 + 720.000
Emecânica = 725.445 J
9. Utilizando as informações do gráfico abaixo:
O enunciado do exercício fornece que a energia mecânica (Em) vale 1.000 J). Observe agora o
gráfico que fornece valores de energia potencial nas posições A, B, C e D. E lembrando que
precisamos determinar a energia cinética nessas posições, utilizaremos a expressão
Em = Ec + Ep onde o valor de Em permanece sempre constante teremos:
Para a posição A
Visualizamos no gráfico que na posição A energia potencial vale 1.000 J e como no enunciado a
energia mecânica vale 1.000 J teremos:
Em = Ec + Ep
1.000 = Ec + 1.000
Ec = 0
Para a posição B
Visualizamos no gráfico que na posição B a energia potencial vale 0 e como no enunciado a
energia mecânica vale 1.000 J teremos:
Em = Ec + Ep
1.000 = Ec + 0
Ec = 1.000 J
Para a posição C
Visualizamos no gráfico que na posição C a energia potencial vale 300 J e como no enunciado a
energia mecânica vale 1.000J teremos:
Em = Ec + Ep
1.000 = Ec + 300
Ec = 700 J
Exercícios complementares
Mecânica
Para a posição D
Visualizamos no gráfico que na posição D a energia potencial vale 600J e como no enunciado a
energia mecânica vale 1.000 J teremos:
Em = Ec + Ep
1000 = Ec + 600
Ec = 400 J
Como conhecemos os valores da energia cinética nas posições solicitadas utilizaremos a
expressão Ec = m.v2 para determinar as velocidades solicitadas:
2
Na posição A
Na posição B
Na posição C
Na posição D
Ec = 0 e m = 20kg
Teremos:
Ec = m.v2
2
0 = 20.v2
2
0 = 20.v2
0 = v2
20
0 = v2
v2 = 0
v=0
Ec = 1.000J e m = 20kg
Teremos:
Ec = m.v2
2
1.000 = 20.v2
2
2.000 = 20.v2
2000 = v2
20
100 = v2
v2 = 100
v = 10 m/s
Ec = 700J e m= 20kg
Teremos:
Ec = m.v2
2
700 = 20.v2
2
1.400 = 20.v2
1.400 = v2
20
70 = v2
v2 = 70
v  8,36 m/s
Ec = 400J e m = 20kg
Teremos:
Ec = m.v2
2
400 = 20.v2
2
800 = 20.v2
800 = v2
20
40 = v2
v2 = 40
v  6,32 m/s
10.
v(km/h)
v(m/s)
18
5
36
10
54
15
72
20
90
25
108
30
360
100
540
150
900
250
1080
300
Exercícios complementares
Mecânica
11.
a) ( V ) Um carro a 18km/h possui maior velocidade que outro a 5 m/s.
b) ( F ) Um carro a 90km/h é mais veloz que outro a 150 m/s.
c) ( V ) Um veículo a 300m/s é mais veloz que outro a 360 km/h.
d) ( V ) Um veículo a 108km/h possui a mesma velocidade que outro a 30 m/s.
e) ( V ) Um carro a 100m/s é menos veloz que um carro a 540 km/h
12.
Tensão (ou tração) no fio (T)
Tensão (ou tração) no fio (T)
Força da gravidade (P)
2.000 N
13.
600 N
600 N
2.000 N
Calculando a força resultante teremos:
Fresultante na horizontal = 600 – 600 = 0
Fresultante na vertical = 2.000 – 2.000 = 0
As resultantes das forças tanto na horizontal quanto na vertical valem zero. Como resultante das
forças que agem sobre o corpo é zero e de acordo com a primeira lei de Newton (lei da inércia), o
corpo pode estar em movimento.
Exercícios complementares
Mecânica
14. A figura que se segue representa as forças que agem sobre um carro:
Fnormal = 2.000 N
Fatrito = 300 N
Fmotora = 1.600 N
Fgravidade = 2.000 N
a. Determine a força resultante que age no carro.
Fresultante na vertical = 2.000 – 2.000 = 0
Não ocorre movimento na vertical
Fresultante na horizontal = 1.600 – 300 = 1.300 N (Fresultante na vertical diferente de zero, logo o corpo possui
aceleração!)
b. Qual o valor da massa do veículo?
Observamos na figura que a força da gravidade (peso) que atua no carro vale 2.000 N e
lembrando da expressão P = m.g teremos:
P = m.g, onde g = 10m/s2
2.000 = m.10
2.000 = m
10
m = 200 kg
c. Qual será então sua aceleração?
Utilizaremos a expressão Fr = m.a:
No item a desse exercício obtivemos que Fr = 1.300 N e no item b temos m= 200 kg. Teremos
então a seguinte aceleração:
Fr = m.a
1.300 = 20.a
1.300 = a
20
a = 6,5 m/s2
Exercícios complementares
Mecânica
15. Tem-se que a freqüência vale f = 10 Hz e  = 3,14
B
A
15cm
30cm
a) a velocidade angular () do ponto A
Como foi fornecido o valor da freqüência f, na determinação da velocidade angular utilizaremos
a expressão  = 2..f
 = 2..f
 = 2.3,14.10
 = 62,8 rad/s
b) a velocidade angular () do ponto B
Como a velocidade angular não depende do raio mas somente da freqüência (ou do período) a
velocidade angular é a mesma em qualquer ponto.
c) a velocidade (v) do ponto A
Utilizaremos a expressão v = .r
Onde r é a distância do ponto A ao centro da circunferência (30cm) e  foi determinado no item a.
v = .r
v = 62,8.30
v = 1.88 4 cm/s
d) a velocidade (v) do ponto B
Utilizaremos a expressão v = .r
onde r é a distância do ponto B ao centro da circunferência (15cm) e  foi determinado no item a.
v = .r
v = 62,8.15
v = 942 cm/s
e) a aceleração centrípeta (ac) do ponto B
Utilizaremos a expressão ac = v2
r
onde r é a distância do ponto B ao centro da circunferência (15 cm) e v foi determinada no item d.
Exercícios complementares
Mecânica
2
ac = v
r
ac = (942)2
15
ac = 887.364
15
ac = 59.157,6 cm/s2
16.
massa (kg)
Peso (N)
Lua
5 kg
5x1,6 = 8N
Marte
5 kg
5x3,72 = 18,6 N
Terra
5 kg
5x10 = 50 N
Júpiter
5 kg
5x26 = 130 N
Exercícios complementares