universidade federal de viçosa

Vestibulando Web Page – www.vestibulandoweb.com.br
- UNIVERSIDADE FEDERAL DE VIÇOSA - PROVA DE FÍSICA DISCURSIVA – VESTIBULAR 2007 –
01) Abaixo estão relacionados alguns
fenômenos térmicos observados no cotidiano, envolvendo as substâncias ou
materiais destacados em negrito:
(1) Temos sensação de “frio” na palma
da mão quando tocamos a maçaneta metálica de uma porta à temperatura ambiente.
(2) Uma garrafa de vidro fechada e
quase cheia de água pode se fragmentar após algum tempo no congelador de
uma geladeira.
(3) Temos sensação de “frio” após ser
jogado álcool à temperatura ambiente
em parte de nosso corpo.
(4) Um fio fino de aço pode atravessar um bloco de gelo sem fragmentálo.
(5) Água à temperatura acima da ambiente e bem abaixo de 100 ºC no interior de um frasco fechado pode ferver
quando se joga água “fria” na parede
externa do recipiente.
(6) Relógios cujos pêndulos são feitos de invar (liga metálica de aço e
níquel) são mais precisos que relógios cujos pêndulos são feitos de aço
comum.
Convergente, pois a imagem está sendo
projetada num anteparo (raios reais).
Uma lente divergente produziria imagens virtuais, formada pelo prolongamento dos raios, que não é o caso.
Seguem-se as propriedades físicas das
substâncias ou materiais destacados
em negrito que podem justificar a ocorrência dos fenômenos listados. Utilizando a numeração estabelecida
acima, faça a correlação entre cada
uma das propriedades e o respectivo
fenômeno por ela explicado:
( ) Ponto de ebulição dependente da
pressão.
( ) Ponto de fusão dependente da
pressão.
( ) Alta condutividade térmica.
( ) Dilatação anômala.
( ) Baixo coeficiente de dilatação.
( ) Baixo calor latente de vaporização.
03) Um resistor variável R é ligado a
uma fonte de corrente contínua, de
força eletromotriz ε e resistência
interna rint, constantes, configurando
um circuito fechado de corrente total
i. Para diferentes valores de R, são
medidas a corrente total do circuito
i e a diferença de potencial de saída
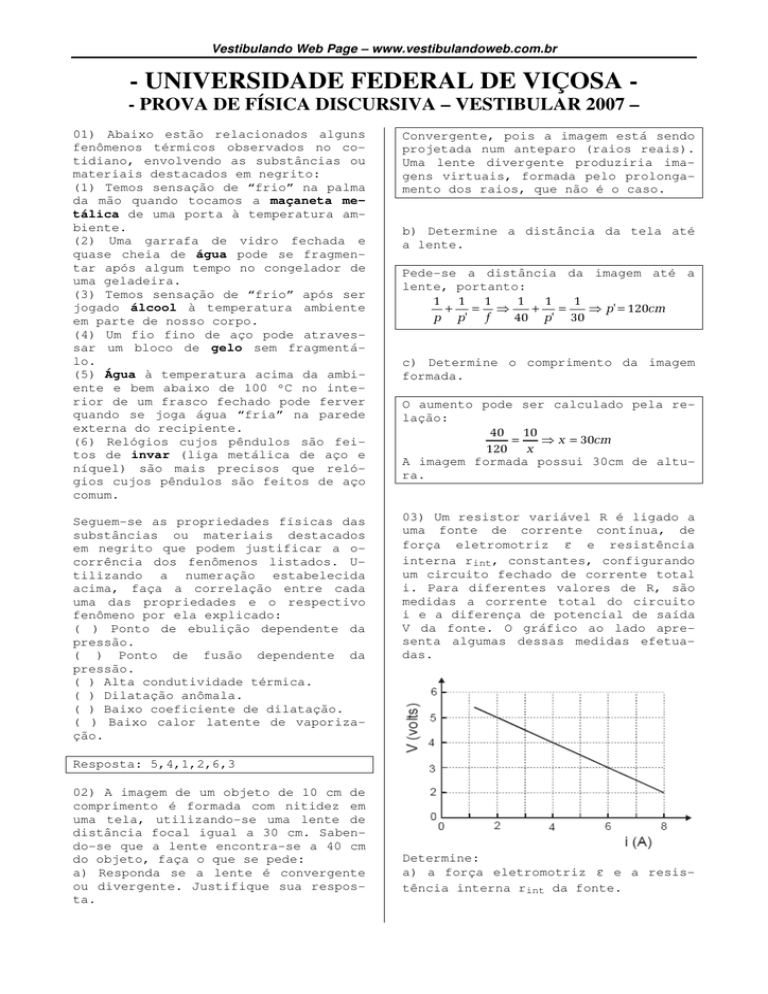
V da fonte. O gráfico ao lado apresenta algumas dessas medidas efetuadas.
b) Determine a distância da tela até
a lente.
Pede-se a distância da imagem até a
lente, portanto:
1 1 1
1
1
1
+
= ⇒
+
=
⇒ p' = 120cm
p p' f
40 p' 30
c) Determine o comprimento da imagem
formada.
O aumento pode ser calculado pela relação:
40 10
=
⇒ x = 30cm
120
x
A imagem formada possui 30cm de altura.
Resposta: 5,4,1,2,6,3
02) A imagem de um objeto de 10 cm de
comprimento é formada com nitidez em
uma tela, utilizando-se uma lente de
distância focal igual a 30 cm. Sabendo-se que a lente encontra-se a 40 cm
do objeto, faça o que se pede:
a) Responda se a lente é convergente
ou divergente. Justifique sua resposta.
Determine:
a) a força eletromotriz ε e a resistência interna rint da fonte.
Vestibulando Web Page – www.vestibulandoweb.com.br
O valor de ε corresponde à tensão VAB
quando o circuito está aberto. Logo,
pelo gráfico vemos que, para circuito
aberto(i=0), temos v = ε = 6V.
Escolha um par de pontos, por exemplo
V=5 e i=2. Para essa situação, se
V=5, sobrou uma ddp de 1V que, certamente, foi consumida pela resistência
interna da bateria. Portanto, aplicando V=RI para ela:
1 = r.2 ⇒ r = 0,50Ω
b) a potência total dissipada em todo
o circuito quando i = 2 A.
A potência total é aquela dissipada
pela soma das duas resistências. Primeiro calculamos o valor de R quando
i=2A. ⇒ 5 = R.2 ⇒ R = 2,5Ω
Com base nessas informações, faça o
que se pede:
a) Obtenha uma expressão para a corrente induzida i na espira em função
de B, L, v e R.
Calcularemos a corrente induzida a
partir de ε = Ri . Portanto, precisamos
encontrar antes o valor de ε.
B.L.L
Como, ε = ∆φ ⇒ ε =
= BLv
∆t
∆t
Portanto,
BLv
ε = Ri ⇒ i =
R
b) Obtenha uma expressão, em função
de B, L, v e R, para o módulo F da
força que deve ser feita na espira
para mantê-la a essa velocidade v .
Nesse caso;
P = Vi = (r + R ).i 2 = (0,5 + 2,5).22 = 12W
c) o valor de V no caso da resistência R ser infinitamente maior que a
resistência rint. Justifique sua resposta.
No caso de R com valores infinitamente altos, teremos uma corrente muitíssimo pequena passando por ele. Como esse valor de corrente também circulará por rint(afinal ela está em série com R)
podemos ver por V=rinti,
que o valor da ddp entre os terminais
de rint será praticamente zero. Logo,
VAB medido será praticamente igual à
F = Bqvsenθ ⇒ F = Bq
L
BLv
⇒F =B
L
∆t
R
v
⇒ F = B 2 L2
R
c) Indique na figura o sentido da
corrente induzida i e a direção e o
sentido da força referida no item anterior.
Usando a regra da “Mão direita”:
i
F
ε.
04) Uma espira de um fio condutor
quadrada, de lado L e resistência elétrica R, é introduzida, com veloci
dade constante v , em uma região que
possui um campo magnético uniforme e
constante B perpendicular à folha de
papel, como ilustrado na figura abaixo.
05) Uma canoa de comprimento L e massa MC encontra-se parada num lago de
águas tranqüilas. Uma pessoa de massa
MP inicialmente em repouso desloca-se
por todo o comprimento dessa embarcação, com velocidade de módulo VP, fazendo a canoa deslocar-se com velocidade de módulo VC. Sabendo que todas
as velocidades são relativas a um observador sentado à margem do lago e
que as forças de atrito envolvendo o
ar e a água são desprezíveis, faça o
que se pede:
a) Responda se o centro de massa do
sistema (canoa + pessoa) permanece em
repouso, em relação ao observador
mencionado, enquanto a pessoa se move. Justifique a sua resposta.
Vestibulando Web Page – www.vestibulandoweb.com.br
O centro de massa permanece em repouso, pois não há forças externas atuando sobre o sistema (canoa + pessoa).
b) Obtenha uma expressão para o módulo da velocidade VC em função de MP,
MC e VP.
Como não há forças externas agindo
sobre o sistema (canoa+pessoa), podemos usar a conservação do momento e
obter:
Q antes = Q depois ⇒ 0 = M P V P − M p + M C VC
(
Vc = −
)
M pV p
M p + Mc
O sinal de “menos” indica que ela está com velocidade na direção oposta a
a VP.
c) Obtenha uma expressão para o módulo D do deslocamento da canoa, também
relativo ao observador, quando a pessoa tiver completado a sua caminhada,
em função de L, MP e MC.
O aluno deverá perceber que a canoa
possui uma aceleração inicial, responsável por colocá-la em movimento.
Porém, a partir de alguns segundos,
essa aceleração assume valor zero,
fazendo com que a canoa tenha um movimento uniforme. A dica é dada na
questão pela expressão “...quando a
pessoa tiver completado a sua caminhada...”
Para a pessoa no final da caminhada e
considerando que a aceleração inicial
agiu em curto intervalo de tempo, podemos usar V p = ∆s ∆t . Substituindo o
valor
do
deslocamento
V p = L ∆t ⇒ ∆t = L
Vp
ficamos
com
Para a canoa, vale a equação equivalente Vc = D ∆t . Substituindo os valores de ∆t e de Vc calculado no item
anterior, ficamos com:
Vc = D ∆t ⇒
M pV p
M p + Mc
Rearranjando,
LM p
⇒D=
M p + Mc
=
D
L
Vp
Resolução: Prof. Rodrigo Marques
Colégio Raiz e Raiz Cursos
Especiais
www.colegioraiz.com.br
(32)3531-7914 - (32)3531-4624