notas de aula - ICEB-UFOP

Bioestatística
October 28, 2013
UFOP
October 28, 2013
1 / 57
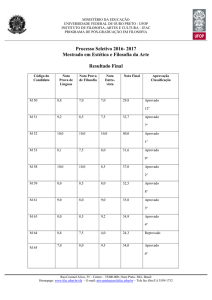
NOME
1
2
Medidas de Tendência Central
Média aritmética
Mediana
Moda
Separatrizes
Medidas de Dispersão
Amplitude Total
Variância e Desvio-padrão
Coeficiente de Variação de Pearson
UFOP
October 28, 2013
2 / 57
Medidas de Tendência Central
Uma medida de tendência central procura sintetizar as informações da
amostra em um único e informativo valor.
As principais medidas de posição estão apresentadas a seguir.
UFOP
October 28, 2013
3 / 57
Média aritmética
A média é a principal medida de posição, sendo utilizada
principalmente quando os dados apresentam distribuição simétrica ou
aproximadamente simétrica, como acontece com a maioria das
situações práticas.
Simbologia:
µ para a média populacional.
X para a média amostral.
UFOP
October 28, 2013
4 / 57
A média populacional é calculada pela expressão a seguir:
Para dados brutos
X1 + X2 + · · · + XN
µ=
⇒µ=
N
em que, N é o tamanho da população.
UFOP
PN
i
Xi
N
October 28, 2013
5 / 57
O estimador da média populacional é:
Para dados brutos
X1 + X2 + · · · + Xn
X=
⇒X=
n
em que, n é o tamanho da amostra.
Pn
i
Xi
n
Para dados agrupados em Tabela de Frequências
Pk
i
X=
Xi fi
n
em que, k é o número de classes.
UFOP
October 28, 2013
6 / 57
Exemplo
Dados Brutos
Vamos voltar ao exemplo das alturas,expressas em centímetros, de 30
atletas do sexo masculino de uma universidade:
168
176
175
172
173
164
170
170
181
181
186
179
169
183
172
173
170
169
164
168
174
175
166
171
182
169
178
177
180
166
A média aritmética será dada por:
X=
X1 + X2 + · · · + Xn
168 + 172 + · · · + 166
⇒X=
n
30
X = 173, 37
UFOP
October 28, 2013
7 / 57
Exemplo
Para dados agrupados em Tabela de Frequências
A tabela de distribuição de frequências foi apresentada na aula
anterior:
UFOP
October 28, 2013
8 / 57
Assim, a média aritmética será dada por:
P5
Xi fi
X = i=1
n
X=
166, 2 · 6 + 170, 6 · 9 + · · · + 183, 8 · 3
= 173, 53
30
UFOP
October 28, 2013
9 / 57
Hipótese Tabular Básica
Alguém pode questionar a razão da diferença observada no uso dos
dois estimadores.
A resposta é dada pela hipótese tabular básica, a qual considera que
todos os elementos de uma classe são representados pelo seu ponto
médio, fato este, que não é verdadeiro em praticamente todas as
situações.
Desta forma, este último resultado é apenas aproximado. No entanto,
o erro cometido é mínimo e, portanto, pode ser desprezado.
UFOP
October 28, 2013
10 / 57
Propriedades da média
A soma algébrica dos desvios em relação à média aritmética é
nula.
n
X
(Xi − X) = 0
i
A soma dos quadrados dos desvios de um conjunto de dados em
relação a sua média e um valor mínimo.
D=
n
X
(Xi − X)2
i
UFOP
October 28, 2013
11 / 57
Propriedades da média
A média de um conjunto de dados acrescido em cada elemento
por uma constante e igual à média original mais essa constante.
∗
X =X +k
∗
em que X é a média do novo conjunto de dados e k é a
constante.
Multiplicando todos os dados por uma constante a nova média
será igual ao produto da média anterior pela constante.
∗
X =X ·k
A média é influenciada por valores extremos.
UFOP
October 28, 2013
12 / 57
Mediana
A mediana divide as observações ordenadas em partes iguais.
Para sua determinação é necessário o conhecimento da posição
central.
Para dados ordenados, temos basicamente têm-se duas situações
distintas:
Se n for par:
md =
X(n/2) + X((n+2)/2)
2
Se n for ímpar:
md =
UFOP
X(n+1)
2
October 28, 2013
13 / 57
Exemplo
Dados ordenados
No caso dos atletas a posição central está entre o 15o e o 16o
elemento.
Portanto, a mediana é a média aritmética destas duas observações.
Logo,
md =
X(15) + X(16)
X(30/2) + X(30+2)/2
⇒ md =
2
2
md = 172, 5cm
UFOP
October 28, 2013
14 / 57
Dados agrupados em Tabela de Frequências
No caso de dados agrupados a mediana pode ser calculada de
acordo com a seguinte expressão:
n/2 − Fant
md = LImd +
· cmd
fmd
em que
fmd é a freqüência da classe mediana;
cmd é a amplitude da classe mediana;
Fant é a frequência acumulada das classes anteriores à classe
mediana;
LImd é o limite inferior da classe mediana.
A classe mediana é a classe que contém a posição n/2 (posição
mediana) da distribuição de freqüência.
UFOP
October 28, 2013
15 / 57
Exemplo
No caso dos atletas temos:
Posição mediana = 30/2 = 15 (contida na 2a classe), Fant = 6;
LImd = 168, 4, fmd = 9 e cmd = 4, 40.
Logo,
15 − 6
· 4, 40
md = 168, 4 +
9
md = 172, 8cm
UFOP
October 28, 2013
16 / 57
Propriedades da mediana
A mediana de um conjunto de dados acrescido em cada elemento
por uma constante e igual à mediana original mais essa
constante.
md∗ = md + k
em que md∗ é a mediana do novo conjunto de dados e k é a
constante.
Multiplicando todos os dados por uma constante a nova mediana
será igual ao produto da mediana anterior pela constante.
md∗ = md · k
UFOP
October 28, 2013
17 / 57
Observação
Muitas vezes existem dúvidas de qual medida utilizar para sintetizar os
dados amostrais.
Como uma regra geral, pode-se definir qual medida é mais
conveniente para uma dada situação com base na análise do
histograma ou do polígono de freqüências.
Se a distribuição dos dados for assimétrica, isto é quando valores
extremos predominam em uma das caudas da distribuição, deve se
preferir a mediana como medida sintetizadora.
Isto se deve ao fato da mediana ser pouco sensível a presença de
valores extremos, sendo considerada mais robusta que a média.
O termo robusto é o termo técnico usado para indicar esta
propriedade da mediana em relação à média aritmética, que quando a
situação de simetria é violada a mediana é uma medida que sofre
menos “interferências” nas suas estimativas.
UFOP
October 28, 2013
18 / 57
Moda
A moda é definida para dados qualitativos ou para quantitativos
discretos como sendo o valor de maior freqüência na amostra.
Para dados quantitativos contínuos a moda é o valor de maior
densidade. Portanto para dados quantitativos contínuos o estimador
da moda é baseado na distribuição de freqüências.
Esse estimador busca encontrar o ponto de máximo do polígono de
freqüências.
Um conjunto pode ter mais de uma moda ou até mesmo não ter moda.
UFOP
October 28, 2013
19 / 57
O estimador da moda para dados quantitativos contínuos é definido a
partir da distribuição de freqüência por meio de um método
geométrico, o qual conduz a seguinte expressão:
mo = LImo +
∆1
· cmo
∆1 + ∆ 2
em que:
LImo : limite inferior da classe modal;
∆1 : diferença entre as freqüências da classe modal e a classe
anterior;
∆2 : diferença entre as freqüências da classe modal e a classe
posterior;
cmo : amplitude da classe modal.
A classe modal é a classe com maior freqüência.
UFOP
October 28, 2013
20 / 57
Propriedades da moda
A moda de um conjunto de dados acrescido em cada elemento
por uma constante e igual à moda original mais essa constante.
mo∗ = mo + k
em que mo∗ é a mediana do novo conjunto de dados e k é a
constante.
Multiplicando todos os dados por uma constante a nova moda
será igual ao produto da moda anterior pela constante.
mo∗ = mo · k
UFOP
October 28, 2013
21 / 57
Relações empíricas entre média, mediana e moda
X = md = mo (distribuição simétrica)
X > md > mo (distribuição assimétrica à direita)
X < md < mo (distribuição assimétrica à esquerda)
UFOP
October 28, 2013
22 / 57
Separatrizes
São as medidas que separam a distribuição de freqüências em partes
iguais.
Vimos que a mediana divide a distribuição em duas partes iguais
quanto ao número de elementos de cada parte.
Agora vamos estudar outras medidas que dividem a distribuição em
partes iguais, que serão as chamadas separatrizes.
Lembrem-se: os dados deves etar ordenados em ordem crescente!!!
UFOP
October 28, 2013
23 / 57
Quartis
Os quartis dividem um conjunto de dados em quatro partes iguais.
Assim:
Q1 : 1o quartil. Deixa 25% dos elementos antes do seu valor
Q2 : 2o quartil. Deixa 50% dos elementos antes do seu valor.
Coincide com a mediana.
Q3 : 3o quartil. Deixa 75% dos elementos antes do seu valor.
UFOP
October 28, 2013
24 / 57
Genericamente, para determinar a ordem ou posição do quartil a ser
calculado, usaremos a seguinte expressão:
EQi = in/4
em que:
i é o número do quartil a ser calculado.
n é o número de observações.
UFOP
October 28, 2013
25 / 57
Para dados não agrupados, vejamos um exemplo simples:
Considere os dados ordenados:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Neste caso temos n = 10
Se eu estiver interessado em encontrar o terceiro quartil, temos:
EQ3 = 3 · 10/4 = 7, 5
Se o número resultante for decimal, a regra é arredondar sempre para
cima. Logo, Q3 = 8.
Assim, 75% dos valores estão abaixo de 8 e 25% dos valores estão
acima de 8 na distribuição de dados apresentada no exemplo.
UFOP
October 28, 2013
26 / 57
Para dados agrupados em classes temos:
EQi − Fant
Qi = LI + c
fQi
em que
LI = limite inferior da classe que contém o quartil desejado
c = amplitude do intervalo de classe
EQi = elemento quartílico
Fant = frequência acumulada até a classe anterior à classe que
contém EQi
fQi = frequência absoluta simples da classe quartílica.
UFOP
October 28, 2013
27 / 57
Decis
Os decis dividem um conjunto de dados em dez partes iguais.
De maneira geral, para calcular os decis, recorreremos à expressão
que define a ordem em que o decil se encontra:
EDi = in/10
em que:
i é o número do decil a ser calculado.
n é o número de observações.
UFOP
October 28, 2013
28 / 57
Para dados não agrupados, vejamos o exemplo anterior:
Considere os dados ordenados:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} em que n = 10
Se eu estiver interessado em encontrar o D6 , temos:
ED6 = 6 · 10/10 = 6
Se o número resultante for inteiro, a regra é fazer a média dele com o
númeor imediatamente posterior a ele na ordem dos dados. Logo,
D6 = 6+7
2 = 6, 5.
Assim, 60% dos valores estão abaixo de 6, 5 e 40% dos valores estão
acima de 6, 5 na distribuição de dados apresentada no exemplo.
UFOP
October 28, 2013
29 / 57
Para dados agrupados em classes temos:
EDi − Fant
Di = LI + c
fDi
em que
LI = limite inferior da classe que contém o decil desejado
c = amplitude do intervalo de classe
Fant = frequência acumulada até a classe anterior à classe que
contém EDi
fDi = frequência absoluta simples da classe que contém EDi .
UFOP
October 28, 2013
30 / 57
Percentis ou Centis
Os percentis dividem um conjunto de dados em cem partes iguais.
O elemento que definirá a ordem do centil será encontrado pelo
emprego da expressão:
ECi = in/100
em que:
i é o número do percentil a ser calculado.
n é o número de observações.
UFOP
October 28, 2013
31 / 57
Para dados não agrupados, consideremos novamente:
Considere os dados ordenados:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Se estivermos interessados em encontrar o P75 , temos:
EP75 = 75 · 10/100 = 7, 5
Como o número resultante é decimal, temos, P75 = 8.
Assim, 75% dos valores estão abaixo de 8 e 25% dos valores estão
acima de 8 na distribuição de dados apresentada no exemplo.
Note que P75 coincide com Q3
UFOP
October 28, 2013
32 / 57
Para dados agrupados em classes temos:
ECi − Fant
Ci = LI + c
fCi
em que
LI = limite inferior da classe que contém o percentil desejado
c = amplitude do intervalo de classe
Fant = frequência acumulada até a classe anterior à classe que
contém ECi
fCi = frequência absoluta simples da classe que contém ECi .
UFOP
October 28, 2013
33 / 57
Exemplo
Com base na tabela de distribuição de frequências abaixo encontre:
Primeiro quartil
Septuagésimo quinto centil
Nono decil
UFOP
October 28, 2013
34 / 57
Exemplo
Tabela 1 - consumo médio de eletricidade (kWh) entre 80
consumidores - RJ - 1980
Consumo (Kwh)
5 ` 25
25 ` 45
45 ` 65
65 ` 85
85 ` 105
105 ` 125
125 ` 145
145 ` 165
UFOP
fi
4
6
14
26
14
8
6
2
FA
4
10
24
50
64
72
78
80
October 28, 2013
35 / 57
Resolução:
Encontrar a posição do primeiro quartil:
EQi = in/4 =
1 · 80
= 20
4
O Q1 está localizado na 20a posição, logo encontra-se na 3a classe.
Então,
EQi − Fant
20 − 10
Qi = LI + c
= 45 + 20
= 59, 29
fQi
14
Interpretação: 25% dos usuários consomem até 59,59 kwh.
De maneira análoga, 75% dos usuários consomem mais de 59,59
kwh.
UFOP
October 28, 2013
36 / 57
Resolução:
Encontrar a posição do septuagésimo quinto percentil:
ECi = in/100 =
75 · 80
= 60
100
O C75 está localizado na 60a posição, logo encontra-se na 5a classe.
Então,
ECi − Fant
60 − 50
Ci = LI + c
= 85 + 20
= 99, 29
fCi
14
Interpretação: 75% dos usuários consomem até 99,29 kwh.
De maneira análoga, 25% dos usuários consomem mais de 99,29
kwh.
UFOP
October 28, 2013
37 / 57
Resolução:
Encontrar a posição do nono decil:
EDi = in/10 =
9 · 80
= 72
10
O d9 está localizado na 72a posição, logo encontra-se na 6a classe.
Então,
72 − 64
EDi − Fant
= 105 + 20
Di = LI + c
= 125
fDi
8
Interpretação: : 90% dos usuários consomem até 125 kwh.
De maneira análoga, 10% dos usuários consomem mais de 125 kwh.
UFOP
October 28, 2013
38 / 57
Medidas de dispersão ou de variabilidade
As medidas de posição não informam sobre a variabilidade dos dados
e são insuficientes para sintetizar as informações amostrais.
Para exemplificar este fato, tem-se a seguir três amostras com a
mesma média:
A = {8, 8, 9, 10, 11, 12, 12}
X A = 10
B = {5, 6, 8, 10, 12, 14, 15}
X B = 10
C = {1, 2, 5, 10, 15, 18, 19}
X C = 10
UFOP
October 28, 2013
39 / 57
Pode-se observar que as amostras diferem grandemente em
variabilidade.
Por esta razão torna-se necessário estabelecer medidas que indiquem
o grau de dispersão, ou variabilidade em relação ao valor central.
Desta forma pode-se afirmar que uma amostra deve ser representada
por uma medida de posição e dispersão.
As principais medidas de dispersão que são:
Amplitude total
Variância e Desvio-padrão
Coeficiente de Variação de Pearson
UFOP
October 28, 2013
40 / 57
Amplitude total
A amplitude total é definida como a diferença entre o maior e o menor
valor de uma amostra.
A = X(n) − X(1)
Note que para os conjuntos de dados A, B, C, temos:
AA = 12 − 8 = 4
AB = 15 − 5 = 10
AC = 19 − 1 = 18
UFOP
October 28, 2013
41 / 57
Desvantagens
A amplitude tem as seguintes desvantagens:
só considerar os valores extremos para o seu cálculo, e
principalmente se houver outlier ela será grandemente afetada;
ser influenciada pelo tamanho da amostra, pois à medida que a
amostra aumenta a amplitude tende a ser maior.
UFOP
October 28, 2013
42 / 57
Variância e Desvio-padrão
A variância é uma medida da variabilidade que considera todas as
observações e, devido às propriedades que possui, é a mais utilizada
na maioria das situações na estatística.
A variância relaciona os desvios em torno da média e sua raiz
quadrada é conhecida como desvio-padrão.
Simbologia
σ 2 para a variância populacional e σ para o desvio-padrão
populacional
s2 para a variância amostral e s para o desvio-padrão amostral
UFOP
October 28, 2013
43 / 57
A variância populacional é dada por:
2
σ =
PN
i=1 (Xi
− µ)2
N
em que N é o tamanho da População.
UFOP
October 28, 2013
44 / 57
A variância amostral é dada por:
Pn
(Xi − X)2
2
s = i=1
n−1
em que n é o tamanho da amostra e (n − 1) é denominado graus de
liberdade..
UFOP
October 28, 2013
45 / 57
Numa amostra de tamanho n deveria ser utilizado este valor (n) como
divisor desta soma de quadrados de desvios.
No entanto, devido a motivos associados a propriedades dos
estimadores, o divisor da variância amostral é dado por n-1 em lugar
de n na expressão do estimador da variância.
A unidade da variância é igual ao quadrado da unidade dos dados
originais. O desvio padrão, por sua vez, é expresso na mesma
unidade do conjunto de dados, sendo obtido pela extração da raiz
quadrada da variância.
UFOP
October 28, 2013
46 / 57
Para o cálculo da variância ou desvio padrão amostral a partir dos
dados elaborados é preferível utilizar as seguintes expressões:
" n
#
P
X
( ni=1 Xi )2
1
2
2
Xi −
s =
n−1
n
i=1
e
√
s=
UFOP
s2
October 28, 2013
47 / 57
Para dados agrupados temos:
" k
#
P
X
( ki=1 fi X i )2
1
2
2
fi X i −
s =
n−1
n
i=1
em que k é o número de classes.
Exemplo
Assim, para os conjuntos de dados A, B, C, temos:
s2A = 3
s2B = 15
sA ∼
= 1, 77
s2C = 56, 57
sB ∼
= 3, 87
sC ∼
= 7, 53
UFOP
October 28, 2013
48 / 57
O Desvio-padrão
A variância é expressa pelo quadrado da unidade de medidad da
variável que está sendo estudada.
Assim, e a variável sob análise for medida em metro, então a variância
será expressa em m2 .
Para melhr interpretar a dispersão de uma variável, usaremos o desvio
padrão, que será expresso na unidade de medida original dos dados.
Trata-se da mais importante das medidas de dispersão, pois indica a
dispersão média absoluta dos dados em torno da própria média
aritmética.
UFOP
October 28, 2013
49 / 57
Interpretação do Desvio-padrão
Numa linguagem mais simplista, devemos ter em mente que o
desvio-padrão mede a variação entre valores. Assim:
Se os valores estiverem próximos uns dos outros, então o
desvio-padrão será pequeno, e conseqüentemente os dados
serão homogêneos. Ou seja, haverá uma grande concentração
de dados em torno da média.
Se os valores estiverem distantes uns dos outros, então o
desvio-padrão será grande, e conseqüentemente os dados serão
heterogêneos. Ou seja, os valores não se concentrarão com tanta
intensidade em torno da média.
UFOP
October 28, 2013
50 / 57
Propriedades
Variância
Somando ou subtraindo uma constante aos dados a variância
não se altera;
Multiplicando todos os dados por uma constante K a nova
variância ficara multiplicada por K 2 .
Desvio-padrão
Somando ou subtraindo uma constante K aos dados o desvio
padrão não se altera;
Multiplicando todos os dados por uma constante K o novo desvio
padrão fica multiplicado por K.
UFOP
October 28, 2013
51 / 57
Coeficiente de Variação de Pearson
A variância e o desvio padrão medem a variabilidade absoluta de uma
amostra.
Portanto, a variabilidade de amostras de grandezas diferentes ou de
médias diferentes não pode ser comparada diretamente pelas
estimativas da variância ou do desvio padrão obtidas.
O desvio padrão ou variância permitem a comparação da variabilidade
entre conjuntos numéricos que possuem a mesma média e a mesma
unidade de medida ou grandeza.
Nos casos em que os conjuntos possuem diferentes unidades ou
possuem médias diferentes, uma medida de dispersão relativa, como
o coeficiente de variação (CV), é indispensável para se comparar à
variabilidade.
UFOP
October 28, 2013
52 / 57
O coeficiente de variação refere-se à variabilidade dos dados
mensurada em relação a sua média, sendo obtido pela expressão
seguinte:
σ
CVp = x100
µ
O estimador do Coediciente de Variação populacional CVp é dado por
CV =
s
x100
X
O coeficiente de variação é a expressão do desvio-padrão como
porcentagem da média do conjunto de dados.
É uma medida adimensional de variabilidade, ou seja, não possui
unidade de medida.
UFOP
October 28, 2013
53 / 57
Algumas regras empíricas para a interpretação do coeficiente
de variação
Se CV < 15% há baixa dispersão → boa representatividade da
média aritmética como medida de posição.
Se 15% ≤ CV < 30% há média dispersão → a representatividade
da média aritmética como medida de posição é apenas regular.
Se CV ≥ 30% há elevada dispersão → a representatividade da
média aritmética como medida de posição é ruim.
UFOP
October 28, 2013
54 / 57
Exemplo
A média e o desvio-padrão da produtividade de duas cultivares de
milho são: X = 4, 0t/ha e sA = 0, 8t/ha para a variedade de
polinização aberta A e X = 8, 0t/ha e sA = 1, 2t/ha para o híbrido
simples B. Qual das cultivares possui maior uniformidade de
produção?
UFOP
October 28, 2013
55 / 57
Se ao inspecionar as estatísticas apresentadas, você respondesse
que variedade de polinização aberta A seia a demaior uniformidade e
que a razão seria o menordesvio padrao apresentado, você teria
cometido um engano.
Embora as unidades não sejam diferentes, as médias das amostras o
são.
Assim, não é correto utilizar uma medida de varabilidade absoluta,
como o desvio-padrão, para compará-las.
O procedimento adequado é calcular o CV para as cultivares e aí sim,
proceder a comparação.
UFOP
October 28, 2013
56 / 57
CVA =
0, 8
x100 = 20%
4, 0
1, 2
x100 = 15%
8
Assim, é fácil observar que o milho híbrido simples (B) é o mais
uniforme, pois possui menor CV do que a variedade de polinização
aberta A.
CVp =
UFOP
October 28, 2013
57 / 57