Exercícios Resolvidos II

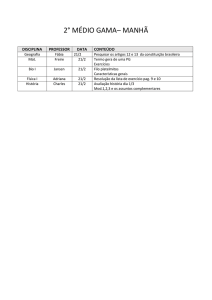
Elementos de Matemática Finita (2016-2017)
Exercı́cios resolvidos
Ficha 3 - 2. Em que classes de congruência mod 8 estão os quadrados
perfeitos?
4926834923 poderá ser a soma de dois quadrados perfeitos?
Resolução: A tabela da multiplicação módulo 8 mostra que os quadrados
perfeitos pertencem às classes de congruência 0, 1 e 4 módulo 8. A tabela da
soma mostra por sua vez que as somas entre estas classes tomam os valores 0,
1, 2, 4 e 5.
Como 4926834923 ≡ 3 mod 8, conclui-se que este inteiro não pode ser a soma
de dois quadrados perfeitos.
Ficha 3 - 6. Resolver as seguintes congruências (encontrar todas as soluções
ou justificar que não existem):
a) 5x ≡ 3 mod 11;
b) 12x ≡ 2 mod 33;
c) 9x ≡ 21 mod 12;
d) 110x ≡ 40 mod 575;
e) 1011x ≡ 1101 mod 1110.
Resolução: a) (5, 11) = 1 e portanto existe solução única; como 9 × 5 ≡ 1
mod 11 concluı́mos que a solução é x ≡ 9 × 3 ≡ 5 mod 11.
b) Neste caso (12, 33) = 3 que não divide 2 pelo que não há solução.
c) (9, 12) = 3 que divide 21 e portanto sabemos que existem 3 soluções não
congruentes entre si; podemos encontrar uma solução notando que
21 = 7 × 3 = 7(12 − 9) ≡ −7 × 9
1
mod 12
pelo que x0 ≡ −7 ≡ 5 mod 12 é solução; as outras podem obter-se somando
múltiplos k(12/3) com 1 ≤ k < 3, ou seja
x1 ≡ x0 + 4 ≡ 9
x2 ≡ x1 + 4 ≡ 1
mod 12;
mod 12
Nota: a solução x2 ≡ 1 é óbvia se notarmos primeiro que 21 ≡ 9 mod 12.
Outro método de resolução passa por resolver primeiro a congruência 3x ≡ 7
mod 4 (dividindo tudo por 3) que tem a solução x ≡ 1 mod 4, e usar o facto
de que um inteiro x satisfaz a congruência inicial 9x ≡ 21 mod 12 se e só se
satisfaz esta última; portanto as soluções da congruência inicial são as classes
de congruência mod 12 queestão contidas na classe 1 mod 4, ou seja 1, 5, 9
mod 12.
d) Como mdc(575, 110) = 5 que divide 40, conclui-se que a equação tem
5 soluções distintas. Aplicando o segundo método de resolução descrito na
alı́nea anterior, começamos por resolver
22x ≡ 8
mod 115 :
o algoritmo de Euclides dá-nos
1 = 9 × 115 − 47 × 22;
portanto a solução desta equação é
x ≡ −47 × 8 ≡ 68 × 8 ≡ 84
mod 115.
As soluções da equação original são as classes módulo 575 contidas na classe
de 84 módulo 115:
84, 199, 314, 429, 544.
A equação
22x ≡ 8 mod 115
também pode ser resolvido com aplicação do Teorema Chinês dos Restos: como
115 = 5 × 23, a soluções desta equação é a solução do sistema

 22x ≡ 8 mod 5
⇔

22x ≡ 8 mod 23
2
⇔

 2x ≡ 3
mod 5
⇔
−x ≡ 8

x≡4
mod 23

⇔

mod 5
x ≡ 15
mod 23
A segunda equação implica que x = 15 + 23y e substituindo na primeira
obtemos
15 + 23y ≡ 4
mod 5 ⇔ 3y ≡ 4
mod 5 ⇔ y ≡ 3
mod 5.
Portanto x = 15 + 23(3 + 5z) = 84 + 115z.
e) O algoritmo de Euclides dá
mdc(1110, 1011) = 3 = 143 × 1110 − 157 × 1011;
como 3 | 1101 a equação tem 3 soluções distintas; como
as soluções são representadas por
1110
3
= 370 e
1101
3
= 367,
−157 × 367, −157 × 367 + 370, −157 × 367 + 2 × 370.
Como a divisibilidade de todas as constantes por 3 é óbvia, podı́amos ter
optado por, dividindo por 3, obter a equação
337x ≡ 367
mod 370 ⇔ −33x ≡ −3
mod 370 ⇔ 11x ≡ 1
mod 370
e obter, pelo algoritmo de Euclides, a solução x ≡ 101 mod 370.
As soluções da equação original são então as classes módulo 1110 de
110,
110 + 370 = 480,
110 + 2 × 370 = 850.
Ficha 3 - 7. Justificar que se ac ≡ bc mod m e d = mdc(c, m), então
a ≡ b mod m/d.
3
Resolução: Temos que, para quaisquer inteiros a e b,
c
c
m
ac ≡ bc mod m ⇔ a ≡ b
mod .
d
d
d
Existem inteiros u e v tais que u dc + v md = 1; como, em particular u é primo
com md , a última congruência é equivalente a
c
c
m
au ≡ bu
mod ,
d
d
d
que por sua vez é equivalente a a ≡ b mod md .
Ficha 3 - 8. Mostrar que todo o inteiro da forma 4k + 3 tem algum factor
da mesma forma. Deduzir que existem infinitos primos congruentes com 3
módulo 4.
Podemos aplicar o mesmo raciocı́nio para inteiros da forma 4k +1? E da forma
6k + 5?
Resolução: Um número m da forma 4k + 3 é ı́mpar e portanto produto
de primos ı́mpares que são congruentes com 1 ou com 3 módulo 4. Mas como
o produto de inteiros congruentes com 1 módulo 4 é também congruente com
1 módulo 4, algum dos factores primos de m terá que ser congruente com 3
módulo 4; aliás, como 32 ≡ 1 mod 4, concluı́mos que na factorização de m em
primos, o número de factores congruentes com 3 módulo 4 é ı́mpar (factores
esses que não têm, evidentemente, que ser distintos).
Este raciocı́nio permite-nos agora copiar a demonstração de Euclides da infinitude de primos: se p1 , · · · , pj forem primos congruentes com 3 módulo 4,
temos que
m = 4 × p1 · · · pj + 3
é congruente com 3 módulo 4; mas, para qualquer 1 ≤ i ≤ j, pi - m. Portanto
tem que existir um primo congruente com 3 módulo 4 distinto dos pi . Se só
existisse um número finito de primos nessas condições, chegarı́amos a uma
contradição.
Este raciocı́nio não se pode aplicar aos inteiros da forma 4k + 1, exactamente
4
porque podemos obter um número congruente com 1 módulo 4 com factores
congruentes com 3 módulo 4. É verdade que existem infinitos primos congruentes com 1 módulo 4, mas esse facto tem que ser provado usando outras
ideias.
Já para os inteiros da forma 6k +5 podemos reproduzir o raciocı́nio feito acima
sem alterações.
Ficha 3 - 9. Seja p primo. Notando que para cada 1 < a < p − 1 existe
um (único) 1 < a0 < p − 1 tal que aa0 ≡ 1 mod p, demonstrar o Teorema de
Wilson:
(p − 1)! ≡ −1 mod p
se e só se p é primo.
Usar o resultado anterior para mostrar que
61! + 1 ≡ 0
mod 71.
Resolução: Embora se possa dar uma demonstração mais directa do Teorema de Wilson, ou mais precisamente de uma das implicações, vamos aproveitar
para apresentar uma outra que nos dá um resultado mais forte, que será aliás
abordado, numa forma mais geral, noutro ponto do curso. Seja p = 2P + 1
um primoı́mpar e a primo com p. Para todo o 0 < x < p existe um e um só
x0 , no mesmo conjunto, satisfazendo
xx0 ≡ a
mod p;
a ideia é considerar separadamente os casos em que x2 ≡ a mod p tem solução
e em que não tem.
Se aquela equação não tem solução, então os p − 1 = 2P inteiros no intervalo
]0, p[ repartem-se em P pares x, x0 tais que
xx0 ≡ a
mod p;
multiplicando estas congruências, obtemos
(2P )! ≡ aP
mod p ⇔ (p − 1)! ≡ a
5
p−1
2
mod p.
Se, pelo contrário, x2 ≡ a mod p tem solução, então tem exactamente duas
soluções x0 e p − x0 (no intervalo ]0, p[, bem entendido): se
x2 ≡ y 2 ≡ a
mod p,
com 0 < x, y < p, então p | (x − y)(x + y) e portanto ou y = x ou y = p − x.
Temos
x0 (p − x0 ) ≡ −a, mod p,
enquanto que os restantes 0 < x < p se repartem em P − 1 pares x, x0 satisfazendo
xx0 ≡ a mod p.
Multiplicando as equações termo a termo obtemos neste casos
(p − 1)! ≡ −a
p−1
2
mod p.
Claro que a = 1 está sempre neste segundo caso e portanto
(p − 1)! ≡ −1
mod p,
o que prova uma das implicações do Teorema de Wilson. A recı́proca, por
outro lado, é imediata, uma vez que se p não for primo, p = u × v, com
0 < u, v < p e portanto (p − 1)! ≡ 0 mod p.
Note-se que, com o facto (p − 1)! ≡ −1 mod p, podemos resumir o que
fizemos no seguinte resultado: se p é um primo ı́mpar e a é primo com p então
verifica-se uma das duas situações:
1. A equação x2 ≡ a mod p tem solução e a
p−1
2
≡ 1 mod p, ou
2. A equação x2 ≡ a mod p não tem solução e a
p−1
2
≡ −1 mod p.
Quanto à última parte do enunciado, sabemos, pelo Teorema de Wilson,
que 70! ≡ −1 mod 71; basta portanto mostrar que
62 × 63 × · · · × 70 ≡ 1
6
mod 71,
o que é equivalente a
(−1)9 9! ≡ 1
mod 71 ⇔ 9! ≡ −1
mod 71,
o que é fácil de verificar directamente (mas sem calcular 9!, bem entendido...).
Ficha 4 - 2. Ao tentar formar grupos de trabalho numa turma, conclui-se
que se os grupos tiverem 3 elementos ficam dois alunos de fora, se tiverem
quatro fica 1 de fora, mas que se consegue formar grupos de 5 elementos desde
que o professor faça parte de um deles. Quantos alunos terá a turma?
Resolução: O problema corresponde à resolução do sistema de congruências

x ≡ 2 mod 3





x ≡ 1 mod 4





x ≡ 4 mod 5
Como os módulos das congruências são primos dois a dois, o Teorema Chinês
dos Restos garante a existência de uma solução única mod 120 (e é de esperar
que o número de alunos de uma turma seja inferior a 120...).
A primeira equação implica x = 2 + 3k; substituindo na segunda ficamos com
3k ≡ −1
mod 4 ⇔ k ≡ 1
mod 4
e portanto
k = 1 + 4j,
x = 2 + 3(1 + 4j) = 5 + 12j
Substituindo na última equação
12j + 5 ≡ 4
mod 5 ⇔ 2j ≡ 4
mod 5 ⇔ j ≡ 2
mod 5
ou seja j = 2 + 5t e portanto x = 5 + 12(2 + 5t) = 29 + 120t.
Ficha 4 - 4. Determinar, usando o Teorema Chinês dos Restos, as soluções,
se existirem, da equação
507x ≡ 312
mod 3025
7
Resolução: Como 3025 = 52 × 112 , a equação é equivalente ao sistema
507x ≡ 312 mod 25
7x ≡ 12 mod 25
⇔
⇔
507x ≡ 312 mod 121
23x ≡ 70 mod 121
aplicando o algoritmo de Euclides,
x ≡ 16 mod 25
⇔
x ≡ −18 mod 121
Em vez de resolver o sistema pelo processo iterativo usado por exemplo na
resolução anterior, vamos determinar a e b satisfazendo as congruências
25a ≡ 1
121b ≡ 1
mod 121
mod 25;
a solução do sistema será, módulo 3025, dada por 16×121b−18×25a. Note-se
que seguimos este caminho unicamente para ilustrar o método e não por ser o
mais prático neste caso.
Resolvemos a equação 25a ≡ 1 mod 121, não por aplicação directa do
algoritmo de Euclides, mas reduzindo o problema à resolução de equações com
módulo 11: se a é solução desta congruência também o é da mesma equação
módulo 11 e temos
25a ≡ 1
mod 11 ⇔ 3a ≡ 1
mod 11 ⇔ a ≡ 4
mod 11.
Portanto a solução da equação original, que tem que existir e é única, será da
forma 4 + 11y. Mas
25(4 + 11y) ≡ 1
⇔ 25y ≡ −9
mod 121 ⇔ 25 × 11y ≡ −99
mod 11 ⇔ 3y ≡ −9
mod 121 ⇔
mod 11 ⇔ y ≡ −3
mod 11,
e portanto a solução pretendida é a ≡ −29 mod 121.
É claro que a equação 25(4+11y) ≡ 1 mod 121 tem 11 soluções y ≡ −3+11k
mod 121, com 0 ≤ k < 11; o que acontece é que o nosso objectivo não é
saber essas soluções y mas sim a ≡ 4 + 11y mod 121 e portanto todas elas
correspondem à mesma classe.
A segunda equação pode resolver-se de modo simples notando que
121b ≡ 1
mod 25 ⇔ −4b ≡ 1
8
mod 25 ⇔ b ≡ 6
mod 25.
Em conclusão, como
16 × 121 × 6 − 18 × 25 × (−29) = 24666 ≡ 466
mod 3025,
a solução do sistema é x ≡ 466 mod 3025.
Ficha 4 - 5. Determinar directamente as soluções de
x3 + 2x − 3 ≡ 0
mod 5
x3 + 2x − 3 ≡ 0
mod 9
e de
e usar as soluções encontradas para determinar as de
x3 + 2x − 3 ≡ 0
mod 45
Resolução: A primeira equação tem soluções x ≡ 1 mod 5 e x ≡ 3
mod 5.
Na segunda equação, em vez de substituir os 9 possı́veis valores, notamos que
x3 +2x−3 ≡ 0
mod 9 =⇒ x3 +2x−3 ≡ 0
mod 3 ⇔ x(x2 +2) ≡ 0
mod 3,
que tem solução única x ≡ 1 mod 3. Portanto as soluções de x3 + 2x − 3 ≡ 0
mod 9 são da forma 1 + 3y, com 0 ≤ y < 3, e é fácil verificar que a única
solução ocorre com y = 0 (mas ver nota abaixo).
Portanto x3 + 2x − 3 ≡ 0 mod 45 tem duas soluções que são as soluções dos
sistemas
x ≡ 1 mod 5
x ≡ 3 mod 5
x ≡ 1 mod 9
x ≡ 1 mod 9
A solução do primeiro sistema é, sem necessidade de qualquer cálculo, x ≡ 1
mod 45; o segundo tem solução x ≡ 28 mod 45.
Nota: É instrutivo notar que (1 + 3y)m ≡ 1 + 3my mod 9, uma vez que
todas as outras parcelas têm um factor 3k com k > 1.
Ou seja, mais geralmente, se procuramos soluções de uma equação
n
X
bi xi ≡ 0 mod p2 ,
i=0
9
podemos primeiro encontrar uma (ou mais) solução a módulo p e procurar
depois soluções da equação original da forma a + py; mas, pela observação que
fizémos,
(a + py)i ≡ ai + ipy mod p2 ,
pelo que a equação se reduz a uma equação linear. Esta ideia generaliza-se
para obter as soluções de equações módulo pk (ver Ficha Complementar sobre
este tema).
Ficha 4 - 6. Mostrar que, dados inteiros positivos m1 e m2 , o sistema
x ≡ a1
mod m1
x ≡ a2
mod m2
tem solução se e só se a1 ≡ a2 mod mdc(m1 , m2 ), e que nesse caso a solução
é única módulo mmc(m1 , m2 ).
Resolução: A demonstração pode fazer-se repetindo o raciocı́nio usado
inicialmente para resolver um sistema com a condição d = mdc(m1 , m2 ) = 1:
x é solução da primeira equação se e só se for da forma x = a1 + m1 y; e, nessa
condição, é solução da segunda equação se e só se
m1 y ≡ a2 − a1
mod m2 ,
que, por sua vez, tem d soluções se d | (a2 − a1 ) e nenhuma caso contrário.
Suponhamos que estamos no primeiro caso e que as soluções são
m2
y0 + k ,
0 ≤ k < d;
d
então x = a1 +m1 y0 +k m1dm2 = a1 +m1 y0 +kmmc(m1 , m2 ) e portanto a solução
é de facto única módulo mmc(m1 , m2 ).
Ficha 5 - 1. Determinar
a) 0 ≤ a < 73 satisfazendo a ≡ 9794 mod 73.
b) 0 ≤ a < 83 satisfazendo a ≡ 7670 mod 83.
10
Resolução: a) Como 73 é primo, sabemos pelo Teorema de Euler (ou
mesmo pelo Teorema de Fermat) que 972 ≡ 1 mod 73. Portanto
11
9794 = 911×72+2 = 972 92
e
972
11
92 ≡ 92 ≡ 8
mod 73
b) Pode aplicar-se o mesmo método uma vez que também 83 é primo.
Como 670 = 8 × 82 + 14, somos conduzidos a calcular 714 mod 83, pelo que
é boa ideia tentar simplificar os cálculos e não calcular todas as potências
72 , 73 , 74 , · · · , 714 ( mod 83 é claro).
Uma forma passa por ver que 14 = 8 + 4 + 2 e
72 = 49 ≡ −34,
73 ≡ 11, 74 ≡ 77 ≡ −6
em que todas as congruências são mod 83, e portanto 78 ≡ 36 mod 83. Logo
714 ≡ (−34) × (−6) × 36 ≡ 40
mod 83.
Ficha 5 - 3. Mostrar que n7 − n é divisı́vel por 42, para todo o inteiro n.
Resolução: n7 − n ≡ 0 mod 42 se e só se
 7
 n − n ≡ 0 mod 7
n7 − n ≡ 0 mod 3
 7
n − n ≡ 0 mod 2
A primeira equação é satisfeita por qualquer inteiro n pelo Teorema de Fermat.
Mas a mesma coisa acontece para as outras equações: por exemplo, como
n3 ≡ n mod 3 temos
n7 − n ≡ n2×3 n − n ≡ n3 − n ≡ 0
mod 3.
Ficha 5 - 4. Mostrar que se p é um primo diferente de 2 e de 5, então p
divide infinitos inteiros do conjunto {9, 99, 999, 9999, · · · }.
11
Resolução: Temos apenas que observar que o inteiro 9 . . . 9 (k noves) é
igual a 10k − 1. Como p é primo com 10, sabemos que 10p−1 ≡ 1 mod p, mas
portanto também
10m(p−1) ≡ 1
mod p ⇔ 10m(p−1) − 1 ≡ 0
mod p,
para qualquer m ≥ 0, o que nos dá uma infinidade de inteiros no conjunto
dado divisı́veis por p.
Ficha 5 - 5. Usando a factorização 561 = 3 ∗ 11 ∗ 17 mostrar que a561 ≡ a
mod 561 para todo o inteiro a.
Resolução: Dado um a fixo, considere-se o sistema

x ≡ a561 mod 3





x ≡ a561 mod 11





x ≡ a561 mod 17
O Teorema de Fermat implica que, dado um primo p
am ≡ am−p ap ≡ am−p+1
mod p;
repetindo este cálculo k vezes, deduzimos que
am ≡ am−kp+k
escolhemos k de modo a que
mod p;
m
m−p
≥k>
;
p−1
p−1
aplicando este raciocı́nio a cada uma das congruências, vemos que o sistema é
equivalente a

x ≡ a mod 3





x ≡ a mod 11 ⇔ x ≡ a mod 561,





x ≡ a mod 17
0 ≤ m − kp + k < p ⇔
12
pelo Teorema Chinês dos Restos.
Ficha 5 - 6. Mostrar que os inteiros 11051 e 294409 não são primos.
Resolução: A resolução deste problema depende da realização de cálculos
impraticáveis sem o uso de um computador. Apresenta-se a solução como
ilustração da aplicação dos resultados apresentados nas aulas.
Se 11051 for primo, o Teorema de Fermat garante que, para qualquer a
primo com 11051,
a11050 ≡ 1 mod 11051;
mas 211050 ≡ 5907 mod 11051.
Se tentamos aplicar o mesmo teste a 294409, verificamos que
a294408 ≡ 1
mod 294409
para a ∈ 2, 3, 5, 7, 11, 13, 17, ...(?).
Mas podemos aplicar o critério de Rabin-Miller: 294408 = 36801 × 8 e verificamos que
236801 ≡ 512 mod 294409
236801×2 ≡ 262144
236801×4 ≡ 1
mod 294409
mod 294409
o que mostra que 294409 não é primo: pondo r = 236801×2 , temos r2 ≡ 1
mod 294409; se este fosse primo, terı́amos que ter r ≡ ±1 mod 294409.
Ficha 5 - 7. Dizemos que n é um pseudo-primo para a base 2 se 2n−1 ≡ 1
mod n mas n não for primo. Mostrar que n é um pseudo-primo para a base
2, então 2n − 1 também o é.
n
Sugestão: Mostrar que 2n − 1 divide 22 −2 − 1.
13
Resolução: A condição na sugestão é verificada porque, uma vez que n é
um pseudo-primo para a base 2, existe k > 0 tal que 2n−1 − 1 = kn; logo
2n −2
2(2n−1 −1)
2kn
n
n
(2k−1)n
2
−1=2
− 1 = 2 − 1 = (2 − 1) 1 + 2 + · · · + 2
.
Por outro lado, 2n − 1 é um pseudo-primo para a base 2 se
n
22
−2
≡1
mod 2n − 1,
que foi o que acabámos de provar.
8. Resolver a equação ou mostrar que não existe solução
a) x85 ≡ 6 mod 29
b) x87 ≡ 5 mod 29
c) x39 ≡ 3 mod 13
d) x123 ≡ 5 mod 24
e) x19 ≡ 5 mod 111
Resolução: a) Como 85 é primo com φ(29) = 28 e 6 é primo com 29, a
equação tem uma única solução. De facto 85 = 1 + 3 × 28 e portanto para
qualquer x primo com 29,
x85 ≡ x
mod 29
e a solução é (a classe de congruência módulo 29 de) 6.
b) A situação é semelhante mas neste caso o algoritmo de Euclides conduz
a
1 = −9 × 87 + 28 × 28;
deduz-se que
59 ≡ x9×87 ≡ x−1+28×28 ≡ x−1
mod 29,
ou seja, a solução da equação é a classe inversa (para a multiplicação) da de
59 . Calculando a potência, temos 59 ≡ 4 mod 29 e portanto a solução é
14
x ≡ −7 ≡ 22 mod 29.
Para evitar a potência −1, podı́amos ter antes escolhido
1 = 19 × 87 − 59 × 28
e ficávamos com
519 ≡ x19×87 ≡ x1+59×28 ≡ x
mod 29.
d) Como φ(24) = 8,
x123 ≡ x8×15+3 ≡ x3
mod 24
para qualquer x primo com 24. Portanto, aplicando outra vez o Teorema de
Euler, a solução é
x ≡ x9 ≡ 53 ≡ 5 mod 24.
e) Em vez de aplicar directamente o Teorema de Euler, podemos começar
por usar o Teorema Chinês dos Restos, uma vez que 111 = 3 × 37:
19
x ≡ 5 mod 3
19
x ≡ 5 mod 111 ⇔
x19 ≡ 5 mod 37
A primeira equação tem solução x ≡ 2 mod 3. Quanto à segunda, temos
1 = 9 × 36 − 17 × 19 = −10 × 36 + 19 × 19
e portanto
x ≡ x1+10×36 ≡ x19×19 ≡ 519 ≡ 32
mod 37.
Ficha 5 - 11. Seja F (m) = φ(d1 )+φ(d2 )+· · ·+φ(dr ) onde os di , 1 ≤ i ≤ r
designam os divisores (positivos) de m.
Exemplo: F (12) = φ(1) + φ(2) + φ(3) + φ(4) + φ(6) + φ(12).
a) Calcular F (5), F (6) e F (10).
15
b) Mostrar que se p é primo, F (p) = p e mais geralmente F (pk ) = pk .
c) Justificar que, se mdc(m, n) = 1, então F (mn) = F (m)F (n).
d) Conclusão?
Resolução: a)
F (5) = φ(1) + φ(5) = 1 + 4 = 5
F (6) = φ(1) + φ(2) + φ(3) + φ(6) = 1 + 1 + 2 + 2 = 6
F (10) = φ(1) + φ(2) + φ(5) + φ(10) = 1 + 1 + 4 + 4 = 10
b) F (p) = φ(1) + φ(p) = 1 + p − 1 = p. Mais geralmente, como os divisores de
pk são os inteiros pi com 0 ≤ i ≤ k,
k
F (p ) =
k
X
i
φ(p ) = 1 +
i=0
k
X
i
φ(p ) = 1 +
i=1
k
X
(pi − pi−1 ) = pk
i=1
P
c) Pela definição, F (mn) = d|mn φ(d); mas, porque m e n são primos entre
si, para cada divisor d de mn existem d1 | m e d2 | n, únicos, tais que d = d1 d2 .
E reciprocamente, a cada par (d1 , d2 ) nestas condições corresponde um divisor
d = d1 d2 de mn. Note-se além disso que d1 e d2 são primos entre si.
Podemos portanto escrever aquele somatório como um duplo somatório: para
cada valor fixo de d1 , somamos as parcelas correspondentes a d | mn da forma
d = d1 d2 em que d2 é um divisor de n; e somamos depois estas somas para
todos os valores de d1 . Ou seja
X
X
X
F (mn) =
φ(d) =
d1 | m
φ(d1 d2 ) =
d2 |n
d|mn
=
X
d1 | m
X
φ(d1 )φ(d2 ) =
X
d1 | mφ(d1
d2 |n
X
d2 |n
d) A conclusão é que F (m) = m para qualquer m.
Ficha 5 - 12.
16
φ(d2 ) = F (m)F (n)
a) Para que valores de m se verifica φ(m) =
m
?
2
b) Existe algum n tal que φ(n) = 50?
c) Para que valores de m é que φ(m) divide m?
Resolução: a) A igualdade verifica-se se e só se m = 2k , k > 0: se m for
dessa forma o resultado é óbvio; por outro lado, se
j Y
m
pi − 1
φ(m) = m
2
pi
i=1
onde p1 , · · · , pj são os primos que ocorrem na factorização de m, então temos
j
Y
i=1
pi = 2
j
Y
(pi − 1)
i=1
que conduz a uma contradição se algum dos pi for ı́mpar.
b) É evidente que n não pode ser uma potência de 2. Seja n = 2k pj11 · · · pjrr
onde pi , 1 ≤ i ≤ r são os primos ı́mpares que dividem n. Então
r
Y
k
φ(n) = φ(2 )
pji i −1 (pi − 1);
i=1
como cada pi contribui pelo menos com um factor 2 para este produto, temos
que para que φ(n) = 50, teria que ser n = 2k pj , com k igual a 0 ou 1, e p um
primo da forma 4t + 3, caso contrário p − 1 teria um factor 22 ; em particular, p
não é 5. Portanto seria 50 = φ(n) = pj−1 (p − 1); mas então, como não há mais
nenhum primo ı́mpar na factorização de 50, teria que ser j = 1 e 50 = p − 1,
mas 51 não é primo. Conclui-se que não existe n tal que φ(n) = 50.
c) Mais uma vez, as potências de 2 são soluções óbvias. Pondo de novo
n = 2k pj11 · · · pjrr onde pi , 1 ≤ i ≤ r são os primos ı́mpares que dividem n, a
condição fica
r
r
Y
Y
ji −1
k
k
φ(2 )
pi (pi − 1) | 2
pji i
i=1
i=1
17
e vemos que tem que ser k > 0 devido aos factores pares pi −1 do lado esquerdo;
simplificando, ficamos com
r
Y
(pi − 1) | 2
i=1
r
Y
pi
i=1
e portanto r = 1. Mas a única solução de (p − 1) | 2p é p = 3. E de facto,
para quaisquer k > 0 e j ≥ 0, φ(2k 3j ) = 2k 3j−1 | 2k 3j .
Ficha 5 - 13. Seja m um número natural livre de quadrados, isto é, existem
primos pi (com 1 ≤ i ≤ k) tais que se i 6= j então pi 6= pj e m = p1 p2 · · · pk .
Supondo que mdc(k, φ(m)) = 1, mostrar que a equação
xk ≡ b
mod m
tem uma única solução, mesmo que mdc(b, m) > 1.
Sugestão: usar o Teorema Chinês dos Restos.
Resolução: A equação é equivalente ao sistema
 k
mod p1
x ≡b
..
.
 k
x ≡b
mod pk
Q
Dado que k é primo com φ(m) = ki=1 φ(pi ), se b for primo com pi a i-ésima
equação do sistema tem solução única. Mas se b não é primo com pi é porque
é congruente com 0 módulo pi e a equação também tem solução única x ≡ 0
mod pi .
Assim, cada equação tem solução única e, mais uma vez pelo Teorema Chinês
dos Restos, a equação original também.
Ficha 6 - 2. Determinar (sem esforço...) a única solução da equação
47x120 + 7x100 + 54x20 + 25x + 2 ≡ 0
18
mod 101
Resolução: Em primeiro lugar, x ≡ 0 mod 101 não é solução; portanto,
como 101 é primo, podemos considerar apenas x primo com 101. Mas então
x100 ≡ 1 mod 101 e a equação simplifica-se:
47x120 + 7x100 + 54x20 + 25x + 2 ≡ 0 mod 101 ⇔
⇔ 47x20 + 7 + 54x20 + 25x + 2 ≡ 0 mod 101 ⇔⇔ 25x ≡ −9 mod 101 ⇔
⇔ −x ≡ −36 mod 101 ⇔ x ≡ 36 mod 101
Ficha 6 - 3. Mostrar que se a = b2 então a não pode ser raiz primitiva de
um primo p ı́mpar.
Sugestão: se a é raiz primitiva, então existe s < p − 1 tal que as ≡ b mod p.
Resolução: as ≡ b mod p e a ≡ b2 implicam que
a2s ≡ b2 ≡ a
mod p
e portanto, como a é primo com p,
a2s−1 ≡ 1
mod p;
mas se a é raiz primitiva isso implica que 2s − 1 é múltiplo de p − 1; mas isso
é impossı́vel porque p − 1 é par e 2s − 1 é ı́mpar.
Ficha 6 - 5. Usar o critério de Euler para determinar quais das seguintes
equações têm solução e qual o seu número
a) x12 ≡ 16 mod 17;
b) x20 ≡ 13 mod 17;
c) x48 ≡ 9 mod 17;
d) x11 ≡ 9 mod 17;
Resolução:
a) mdc(12, 16) = 4 e 1616/4 ≡ 1 mod 17 logo a equação tem 4 soluções.
19
b) mdc(20, 16) = 4 e 1316/4 ≡ 1 mod 17 logo a equação tem 4 soluções.
c) Neste caso nem é necessário usar o critério de Euler: mdc(48, 16) = 16 e
portanto, para qualquer x primo com 17,
3
x48 = x16 ≡ 1 mod 17;
logo a equação não tem soluções.
16
Usando o critério, terı́amos obviamente que 9 16 6≡ 1 mod 17, o que nos
dá a mesma conclusão.
d) Como mdc(11, 16) = 1 (e 9 é primo com 17) esta equação tem solução
única.
Ficha 6 - 6. Mostrar que 38 ≡ −1 mod 17. Justificar porque é que
podemos concluir que 3 é raiz primitiva de 17.
Usar uma lista das classes de congruência de 3i mod 17 para encontrar as
soluções do problema anterior.
Resolução: Confirmamos que 38 ≡ −1 mod 17: por exemplo, podemos
abreviar o cálculo notando que
32 ≡ −8
mod 17,
34 ≡ 64 ≡ −4
mod 17;
portanto, como os únicos divisores de φ(17) = 16 são as potências 2k , com
0 ≤ k ≤ 4, concluı́mos que a ordem de 3 módulo 17 tem que ser 16 (se fosse
2k para algum k < 4, então 38 ≡ 1). Com a tabela
a 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3a 1 3 9 10 13 5 15 11 16 14 8 7 4 12 2 6 1
podemos calcular que x será solução da equação em a) se for da forma 3y ,
com y solução de 12y ≡ 8 mod 16, e portanto as soluções são
32 ≡ 9
36 ≡ 15
310 ≡ 8
20
314 ≡ 2.
Já para b) temos as soluções 3y , com y solução de 20y ≡ 4 mod 16:
31 ≡ 3
35 ≡ 5
39 ≡ 14
313 ≡ 12.
Também podemos determinar a solução da última equação que é 3y , com y
solução de 11y ≡ 2 mod 16: como a solução desta última equação é y ≡ 6
temos que a solução de d) é 36 ≡ 15.
Ficha 6 - 7. Sabendo que 5 é uma raiz primitiva de 47 e que 516 ≡ 17
mod 47, determinar as soluções da equação “exponencial”
25x ≡ 17
mod 47
Resolução: As condições do problema implicam
52x ≡ 17 ≡ 516
mod 47
e portanto, como 5 é raiz primitiva,
2x ≡ 16
mod 46
que tem soluções 8 e 31.
Ficha 6 - 8. Se p é um primo ı́mpar, para quantos a ∈ Z/p é que
x2 ≡ a
mod p
tem solução?
Sugestão: Seja g uma raiz primitiva de p e g k ≡ a. Estudar a existência de
solução em função da paridade de k.
Resolução: Por aplicação do critéri ode Euler, a equação tem solução se
a ≡ 1 mod p.
Se g é raiz primitiva de p e a ≡ g k ,
p−1
2
ap−1 2 ≡ g
k(p−1)
2
21
≡1
mod p
se e só se k é par, pois o expoente tem que ser múltiplo da ordem de g, que é
p − 1.
Ficha 6 - 9. Mostrar que se p é primo ı́mpar então
x2 ≡ −1
mod p
tem solução se e só se p ≡ 1 mod 4.
p−1
Resolução: Pelo critério de Euler, a equação tem solução se e só se (−1) 2 ≡
1 mod p, o que acontece exactamente se o expoente for par, ou seja, se p ≡ 1
mod 4..
Ficha 6 - 11. Mostrar que se p e q são primos ı́mpares diferentes e a é
primo com pq,
aφ(pq)/2 ≡ 1 mod pq.
Concluir que pq não tem raizes primitivas.
Resolução: Pelo teorema Chinês dos Restos, a equação é equivalente ao
sistema
(
(q−1)/2
φ(pq)/2
a
≡ 1 mod p
ap−1
≡ 1 mod p
⇔
(p−1)/2
aφ(pq)/2 ≡ 1 mod q
aq−1
≡ 1 mod q
e ambas as equações são satisfeitas por qualquer a primo com p e q, pelo
Teorema de Fermat.
A conclusão é óbvia: nenhum a tem ordem φ(pq) módulo pq.
Ficha 6 - 12. Sendo p um primo ı́mpar e a e k inteiros positivos, usar o
Teorema do binómio para mostrar que
k
k
k
(a + p)φ(p ) ≡ aφ(p ) − pk aφ(p
)−1
mod pk+1 .
Sugestão: Tem que se mostrar que, para j ≥ 2,
k φ(p ) j
p ≡ 0 mod pk+1 ;
j
22
começar por mostrar que pj−1 não divide j!.
Resolução: pelo Teorema do Binómio, temos
X φ(pk )
k
k
k
k
(a + p)φ(p ) = aφ(p ) + φ(pk )aφ(p )−1 p +
aφ(p )−j pj ;
j
j≥2
como
φ(pk )aφ(p
k
)−1
p = (pk −pk−1 )paφ(p
k
)−1
= pk (p−1)aφ(p
k
)−1
≡ −pk aφ(p
k
)−1
mod pk+1 ,
o resultado equivale a mostrar que a soma dos restantes termos é congruente
com 0 módulo pk+1 .
Vamos mostrar que de facto cada uma das parcelas satisfaz esta congruência:
k φ(p ) φ(pk )−j j (pk − pk−1 )(pk − pk−1 − 1) · · · (pk − pk−1 − j + 1) φ(pk )−j j
a
p;
a
p =
j!
j
se j! = pl S, onde S é primo com p, ficamos com, pondo em evidência potências
de p,
k
k−1
− 1) · · · (pk − pk−1 − j + 1) φ(pk )−j
k−1+j−l (p − p
p
a
;
S
k φ(p )
note-se que, como
é um inteiro, e S é primo com p, a fracção na
j
última expressão representa de facto um inteiro. Se conseguirmos provar que
pk−1+j−l ≡ 0 mod pk+1 , temos o resultado pretendido. Ora esta condição é
equivalente a k − 1 + j − l ≥ k + 1, ou seja, a j − 2 ≥ l. É isso que justifica a
última parte da sugestão.
Mas, num exercı́cio anterior, vimos que a maior potência de p que divide j!
(ou seja, o inteiro l ) é dado pela fórmula
X j
l=
b i c;
p
i≥1
evidentemente, podemos majorar esta soma por
X j
1/p
j
j
=j
=
≤
i
p
1 − 1/p p − 1 2
i≥1
23
uma vez que p é ı́mpar. Mas então l < j/2 ≤ j − 1 (j ≥ 2!), como querı́amos
mostrar.
Ficha 6 - 13. Supondo que a no exercı́cio anterior é uma raiz primitiva
para pk , mostrar que então a ou a + p (ou ambos) é raiz primitiva para pk+1 .
Concluir que pn (com p primo ı́mpar) tem sempre raizes primitivas.
Sugestão: Quais os possı́veis valores de ordpk+1 (a)?
Resolução: Temos que mostrar que ou a ou a + p tem ordem módulo pk+1
igual a φ(pk+1 ) = pk+1 − pk . Suponhamos que t = ordpk+1 (a) < pk+1 − pk ; pelas
propriedades elementares da ordem, t tem que dividir pk+1 − pk = pk (p − 1);
mas por outro lado,
at ≡ 1
mod pk+1 =⇒ at ≡ 1
mod pk
e, como estamos a supor que a é raiz primitiva módulo pk , as mesmas propriedades implicam que φ(pk ) | t. Temos então pk−1 (p − 1) | t | pk (p − 1) e,
como t =< pk+1 − pk , só pode ser t = pk−1 (p − 1) = φ(pk ).
Usamos agora o exercı́cio anterior para calcular ordpk+1 (a + p): ficamos com
k
k
(a + p)φ(p ) ≡ aφ(p ) − pk aφ(p
k
)−1
mod pk+1 ≡ 1 − pk aφ(p
k
)−1
mod pk+1 ;
note-se que o lado direito na última congruência não é congruente com 1
módulo pk+1 . Deduzimos que ordpk+1 (a + p) = pk s para algum divisor s de
p − 1. Mas então
X pk s k
k
k
1 ≡ (a + p)p s ≡ ap s +
ap s−j pj mod pk ;
j
j≥1
ora, repetindo o raciocı́nio feito no exercı́cio anterior, verificamos que cada
k
parcela deste último somatório é congruente com 0 módulo pk ; portanto ap s ≡
1 mod pk o que implica, pela hipótese de a ser raiz primitiva módulo pk ,
φ(pk ) | pk s
e portanto (p − 1) | s, ou seja, s = p − 1 e ordpk+1 (a + p) = pk (p − 1) = φ(pk+1 )
e a + p é raiz primitiva módulo pk+1 .
24