RADIOATIVIDADE

QUÍMICA - 2o ANO
MÓDULO 31
RADIOATIVIDADE PARTE 2
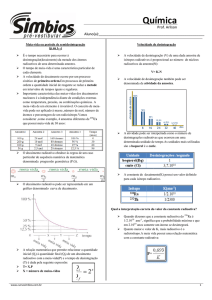
T
massa ativa
veloc. desint
% ativa
300 dpm
100%
T
150 dpm
50%
T
75 dpm
25%
37,5 dpm
12,5%
massa ativa
20g
10g
5g
2,5g
átomos ativos
fração radioativa
X
1
X/2
1/2
X/4
1/4
X/8
1/8
atividade 100%
da amostra
50%
25%
T1
T2
T3
T4
T5 nº de meias-vidas
pressurizador
torre de
transmissão
vapor
vaso de
pressão
gerador
elétrico
turbina
barras de
controle
condensador
gerador
de vapor
bomba
elemento
combustível
água
bomba
bomba
bomba
tanque com água
de alimentação
Como pode cair no enem
(UNIRIO) Cientistas que estudam o Sol disseram que colunas de plasma que se desprendem da
estrela funcionam como canos de um órgão de igreja, fazendo ressoar explosões que ocorrem na
coroa solar. (...) O estudo de como o plasma se aquece poderia acelerar o desenvolvimento da
tecnologia de fissão nuclear em escala industrial. A fissão nuclear é o processo que dá energia
ao Sol e a outras estrelas. Diferentemente dos processos em que há queima de combustíveis
fósseis, na fissão nuclear, não há geração de dióxido de carbono.
(O Globo, 2007)
Em relação à fissão nuclear, pode-se dizer que:
a) a reação de onde os núcleos do hidrogênio se fundem para formar núcleos de hélio é um
exemplo desse processo.
b) o processo é, usualmente, livre de resíduos radioativos.
c) o núcleo original quebra-se em dois, ou mais, núcleos menores, o que libera uma grande
quantidade de energia.
d) ocorre a liberação de anidrido carbônico no processo.
e) este processo leva à formação, apenas, de elementos químicos com o mesmo número de
prótons que o elemento químico original.
Fixação
F
1) (UERJ) Considere o gráfico da desintegração radioativa de um isótopo:
2
n
nº de mol da átomos
1,6
g
o
c
p
0,8
0,4
0,2
0,1
0,05
m
n
v
Para que a fração de átomos não desintegrados seja 12,5% da amostra inicial, o número
a
necessário de dias é:
b
a) 10
c) 20
c
b) 15
d) 25
5
10
15
20
25
Fixação
2) Os cientistas descobriram que, com a mesma velocidade com que o carbono 14 se forma
na alta atmosfera, ele se desintegra segundo a reação:
14
14
0
6 7-1
C → N + β
Desse modo, como ele se forma e se desintegra com a mesma velocidade, sua porcentagem no planeta permanece constante, sendo exatamente a mesma na atmosfera e em todos
os seres vivos (10 ppb). Ao examinar múmias, ossos fósseis e outros achados arqueológicos
compostos por restos de seres vivos os cientistas encontraram neles teores menores que 10
ppb, o que tornou possível determinar-se a idade do material utilizado.
Com base nessas informações, uma amostra de carvão mineral, originado pelo soterramento de gigan-tescas árvores, foi analisada e revelou conter 12,5% de carbono 14 existente
na atmosfera. Há quanto tempo foram soterradas essas árvores? Considere o tempo de meia
vida do carbono 14 como sendo igual a 5600 anos.
o
a) 28300 anos. d) 16800 anos.
b) 20200 anos. e) 18000 anos.
c) 10540 anos.
Fixação
F
3) (CEFET) Quanto mais cedo o paciente usar altas doses de radiação beta, maior será a possibili-4
dade de atrasar ou até mesmo de frear o avanço da esclerose múltipla, segundo pesquisa publicadav
no New England Journal of Medicine, em setembro de 2000. Sendo assim podemos imaginar oa
Bi-210 como uma possível alternativa para o tratamento da esclerose múltipla. Se, após 1 hora, aU
radiação do Bi-210 diminui para 12,5% do valor inicial, a sua meia-vida é de:
p
a) 20 minutos. d) 50 minutos.
D
b) 30 minutos. e) 60 minutos.
a
c) 40 minutos.
b
c
Fixação
4) (FUVEST) O isótopo 14 do carbono emite radiação β, sendo que 1 g de carbono de um vegetal
vivo apresenta cerca de 900 decaimentos β por hora _ valor que permanece constante, pois
as plantas absorvem continuamente novos átomos de 14C da atmosfera enquanto estão vivas.
Uma ferramenta de madeira, recolhida num sítio arqueológico, apresentava 225 decaimentos β
por hora por grama de carbono. Assim sendo, essa ferramenta deve datar, aproximadamente, de:
Dados: tempo de meia-vida do 14C = 5700 anos
a) 19 100 a.C.
d) 7 400 a.C.
b) 17 100 a.C.
e) 3 700 a.C.
c) 9 400 a.C.
Fixação
5) (FUVEST) O isótopo radioativo Cu-64 sofre decaimento β, conforme representado:
64
64
0
29 30-1
C→ Zn + β
A partir de amostra de 20,0 mg de Cu-64, observa-se que, após 39 horas, formaram-se 17,5
mg de Zn-64. Sendo assim, o tempo necessário para que metade da massa inicial de Cu-64 sofra
decaimento β é cerca de:
a) 6 horas.
d) 26 horas.
b) 13 horas. e) 52 horas.
c) 19 horas.
Fixação
6) (FUVEST) Em 1995, o elemento de número atômico 111 foi sintetizado pela transformação
nuclear:
84
28Ni
272
+ 209
83Bi → 111Rg + nêtron
Esse novo elemento, representado por Rg, é instável. Sofre o decaimento:
272
111Rg
264
260
258
252
→ 268
109Mt → 107Bh → 105Db → 103Lr → 101Md
Nesse decaimento, liberam-se apenas:
a) nêutrons.
d) partículas β.
b) prótons.
e) partículas α.
c) partículas α e partículas β.
Fixação
7) (ENEM) O lixo radioativo ou nuclear é resultado da manipulação de materiais radioativos,
utilizados hoje na agricultura, na indústria na medicina, em pesquisas científicas, na produção de
energia etc. Embora a radioatividade se reduza
com o tempo, o processo de decaimento radioativo de algumas matérias pode levar milhões de
anos. Por isso, existe a necessidade de se fazer
um descarte adequado e controlado de resíduos
dessa natureza. A taxa de decaimento radioativo
é medida em termos de um tempo característico,
chamado meia-vida, que é o tempo necessário
para que uma amostra perca metade de sua
radioatividade original.
O gráfico seguinte representa a taxa de
decaimento radioativo do rádio-226, elemento
químico pertencente à família dos metais alcalinos terrosos e que foi utilizado durante muito
tempo na medicina.
F
1kg
8
p
m
r
p
1/2 kg
1/4 kg
1/8 kg
f
As informações fornecidas mostram que: n
d
a) quanto maior é a meia-vida de uma substância mais rápido ela se desintegra.
b) apenas 1/8 de uma amostra de rádio-226a
terá decaído ao final de 4.860 anos.
b
c) metade da quantidade original de rádio-226,c
ao final de 3.240 anos, ainda está para decais.d
d) restará menos de 1% de rádio-226 emc
qualquer amostra dessa substância apóse
decorridas 3 meias-vidas.
m
e) a amostra de rádio-226 diminui sua quantidade pela metade a cada intervalo de 1.620
anos devido à desintegração radioativa.
1620
3240
4560
Anos
Fixação
8) (ENEM) A energia geotérmica tem sua origem no núcleo derretido da Terra, onde as temperaturas atingem 4 000ºC. Essa energia é primeiramente produzida pela decomposição de
materiais radiativos dentro do planeta. Em fontes geotérmicas, a água, aprisionada em um
reservatório subterrâneo é aquecida pelas rochas ao redor e fica submetida a altas pressões,
podendo atingir temperaturas de até 370ºC sem entrar em ebulição.
Ao ser liberada na superfície, à pressão ambiente, ela se vaporiza e se resfria, formando
fontes ou gêiseres. O vapor de poços geotérmicos é separado da água e é utilizado no funcionamento de turbinas para gerar eletricidade. A água quente pode ser utilizada para aquecimento
direto ou em usinas de dessalinização.
Sob o aspecto da conversão de energia, as usinas geotérmicas:
a) funcionam com base na conversão de energia potencial gravitacional em energia térmica.
b) transformam inicialmente a energia solar em energia cinética e, depois, em energia térmica.
c) podem aproveitar a energia química transformada em térmica no processo de dessalinização.
d) assemelham-se às usinas nucleares no que diz respeito à conversão de energia térmica em
cinética e, depois, em elétrica.
e) utilizam a mesma fonte primária de energia que as usinas nucleares, sendo, portanto, semelhantes os riscos decorrentes de ambas.
Fixação
F
100
90
9) (ENEM) A duração do efeito de alguns
fármacos está relacionada à sua meia-vida,
tempo necessário para que a quantidade
original do fármaco no organismo se reduza
à metade. A cada intervalo de tempo correspondente a uma meia-vida, a quantidade de
fármaco existente no organismo no final do
intervalo é igual a 50% da quantidade no início
desse intervalo.
O gráfico representa, de forma genérica, o
que acontece com a quantidade de fármaco no
organismo humano ao longo do tempo.
1
c
d
% de fármaco no organismo
80
70
60
a
b
50
40
30
20
10
0
0
1
2
3
4
5
6
7
número de meias-vidas
(FUCHS. D. e WANNMA Cher l. Farmacologia Clínica.
Rio de Janeiro: Guanabara Koogan,1992, p. 40.)
A meia-vida do antibiótico amoxicilina é de 1
hora. Assim, se uma dose desse antibiótico for
injetada às 12h em um paciente, o percentual
dessa dose que restará em seu organismo às
13h 30 min será aproximadamente de
a) 10%
d) 35%
b) 15%
e) 50%
c) 25%
Fixação
10) (UERJ) A meia-vida é o parâmetro que indica o tempo necessário para que a massa de uma
certa quantidade de radioisótopos se reduza à metade de seu valor. Considere uma amostra
de 53I133, produzido no acidente nuclear, com massa igual a 2 g e meia-vida de 20 h.
Após 100 horas, a massa dessa amostra, em miligramas, será cerca de:
a) 62,5
c) 250
b) 125
d) 500
Fixação
11) (ENEM) A energia térmica liberada em
processos de fissão nuclear pode ser utilizada
na geração de vapor para produzir energia
mecânica que, por sua vez, será convertida
em energia elétrica. Abaixo está representado
um esquema básico de uma usina de energia
nuclear.
Vapor
Água
-
Turbina Gerador
-
-
Com relação ao impacto ambiental causado
pela poluição térmica no processo de refrigeração da usina nuclear, são feitas as seguintes
afirmações:
I) O aumento na temperatura reduz, na água do
rio, a quantidade de oxigênio nela dissolvido,
que é essencial para a vida aquática e para a
decomposição da matéria orgânica.
II) O aumento da temperatura da água modifica
o metabolismo dos peixes.
III) O aumento na temperatura da água diminui o crescimento de bactérias e de algas,
favorecendo o desenvolvimento da vegetação.
Das afirmativas acima, somente está(ão)
correta(s):
a) I
d) I e II
b) II
e) II e III
c) III
Proposto
1) (UFRRJ) Para determinar a constante de Avogadro, Rutherford observou a seguinte série
radioativa:
88
R226 → 86Rn → 54Po → 82Pb → 83Bi → 84Po → 82Pb
A partir desta série, responda:
a) Qual a relação entre o número de partículas α e partículas β emitidas na série radioativa
acima? Justifique.
b) Sabendo que a meia-vida do Polônio-218 é de 3,1 minutos, calcule o tempo que uma amostra
leva para desintegrar 87,5% de sua massa.
Proposto
2) (UFRJ) A concentração de carbono 14 nos seres vivos e na atmosfera é de 10 ppb (partes
por bilhão). Esta concentração é mantida constante graças às reações nucleares representadas
a seguir, que ocorrem com a mesma velocidade.
Ocorre nas camadas mais altas da atmosfera.
Ocorre na camadas mais baixas da atmofesra e nos seres vivos.
A análise de um fragmento de um fóssil de 16.800 anos de idade revelou uma concentração
de carbono 14 igual a 1,25 ppb.
a) Identifique as partículas X e Y.
b) Calcule a meia-vida do carbono 14.
Proposto
s3) (UFRJ) Glenn T. Seaborg é um renomado cientista que foi agraciado com o Prêmio Nobel
sde Química de 1951 por seus trabalhos em radioquímica. Em 1974 foi sintetizado, nos Estados
Unidos, o elemento de número atômico 106 que, em sua homenagem, teve como nome proposto
Seaborgium (106Sg), ainda não homologado.
a) O bombardeio do (98Cf 249) por um elemento X produz o 106Sg263 e 4 nêutrons. Determine o
número atômico e o número de massa do elemento X.
b) Sabendo que um determinado isótopo do 106Sg perde 50% de sua massa inicial em 10 segundos, calcule a massa final de uma amostra de 800 gramas deste isótopo após 30 segundos.
Proposto
4) (UERJ) No tratamento de tumores cancerígenos, recomenda-se a radioterapia, que consiste
em tratar a área atingida pelo câncer com a radiação emitida pelo cobalto-60. Esse isótopo tem
sua meia-vida igual a 5,25 anos e se desintegra espontaneamente, emitindo partículas beta e
produzindo níquel-60 estável. Uma amostra radioativa de massa 200 g, constituída por 95%
de cobalto-59 e 5% de cobalto-60, foi colocada em um aparelho radioterápico.
a) Sabendo que o cobalto-59 é estável, determine a relação entre a massa de níquel-60 produzida e a massa de cobalto-60 restante, após 21 anos.
b) Comparando os raios do cobalto metálico e do íon de cobalto III, cite o que apresenta menor
tamanho e o elétron diferenciador da espécie iônica cobalto III.
Proposto
e5) (UNIRIO) Considerando que a meia-vida do 214Bi é de 20 meses calcule, a partir de uma
amostra com 1,000 g de 214Bi, quantos miligramas restarão depois de 5 anos?
-
r
Proposto
6) (UNIRIO) A dose terapêutica com Iodo-131(131I), também conhecida como radioiodoterapia,
é um tratamento complementar para a maioria dos tumores de tireóide já operados. A meia
vida deste isótopo é de cerca de 8 dias. Partindo-se de 8,0 gramas, calcule a massa de 131I
restante após 40 dias.
Proposto
7) (UFRRJ) As células cancerosas são mais fracas que as normais e, por esse motivo, uma dose
controlada de radiação incidindo apenas sobre o local do tumor pode matar apenas as células
Icancerosas. Esse é o princípio da chamada radioterapia do câncer. O cobalto 60, usado no
tratamento do câncer, possui tempo de meia vida de aproximadamente 5 anos. Observou-se,
por exemplo, que uma amostra desse, radionúcleo colocada em uma cápsula lacrada e aberta
após 20 anos continha 750 mg de cobalto 60.
a) Qual a quantidade de cobalto 60 colocada inicialmente na cápsula?
b) Qual a porcentagem de material que restou da amostra inicial?
Proposto
8) (UNESP) O iodo 131(131
I) ainda é muito utilizado como traçador radioativo para exames da
53
glândula tireoide. Entretanto, nos últimos anos vem sendo substituído pelo iodo 123(131
53I), tão
eficiente quanto o iodo 131 para essa finalidade, e que passou a ser produzido no Brasil pelo
Instituto de Pesquisas Energéticas e Nucleares, IPEN. A substituição pelo 123
53I traz vantagens
para os pacientes e para o meio ambiente, pois a radiação γ produzida é de menor energia,
não há emissão de partículas β e a meia-vida é menor.
Sabe-se que a partícula β corresponde a um elétron (-10 e), que a radiação γ é um tipo de
radiação eletromagnética — como o é a luz — e que os processos ocorrem de acordo com as
informações apresentadas nos esquemas a seguir:
I → yxXe + β + γ com Eβ = 0,61 MeV, Eγ = 364 keV e t1/2 = 8 dias.
123
53
123
53
I → 123
53I + γ com E γ = 159KeV e t1/2 = 1/2 dia
a) Determine o número de prótons e de nêutrons existentes em cada átomo de iodo 131 e em
cada átomo de xenônio produzido.
b) Sabendo que as técnicas empregadas nesse tipo de exame se baseiam na medida da
quantidade de radiação emitida em um determinado intervalo de tempo, explique por que são
necessárias menores quantidades de átomos do isótopo radioativo quando se utiliza 123
I em
53
substituição ao 131
I.
53
Proposto
a9) (FUVEST) O cobalto-60 (27Co60), usado em hospitais, tem meia-vida de 5 anos.
Calcule quantos mols de cobalto-60 restarão após 20 anos em uma amostra que inicialmente
continha 10g desse isótopo.
s
m
o
m
Proposto
10) (UFRJ) Um dos produtos liberados nas explosões nucleares e nos acidentes em usinas
nucleares que mais danos pode causar aos seres vivos é o isótopo do estrôncio de número
de massa igual a 90 (estrôncio-90). Ele é um isótopo radiativo que se acumula nos ossos, por
substituição do cálcio, e é emissor de partículas beta. com meia-vida de 28 anos.
a) Se um indivíduo ao nascer absorver em seu organismo o estrôncio-90, com que idade terá
a ação radiativa deste isótopo reduzida a 1/4?
b) Escreva a reação do decaimento radiativo do estrôncio-90, identificando o elemento que
dele se origina.