Flambagem de Colunas

ENG01140 – Turma C (Prof. Alexandre Pacheco)
15
45
FLAMBAGEM DE COLUNAS
Introdução
É de conhecimento comum que elementos submetidos a carregamentos axiais
tendem a sofrer colapsos de natureza bastante brusca quanto maior forem suas relações de
comprimento por área de seção transversal (experimento simples: régua escolar
comprimida axialmente). Logo, fica bastante claro que um efeito devido a aspectos
geométricos do elemento toma parte do fenômeno. Na medida em que o comprimento vai
sendo encurtado, a carga de ruptura tende a aumentar. Ou seja, para um elemento como
uma coluna curta, este tipo de ruptura passa a ser menos importante e as características do
material de que a coluna é feita é que começam a pesar mais no comportamento do
elemento frente às cargas. Assim, é de suma importância que se determine qual seria o
comprimento, para uma coluna, por exemplo, que seria o divisor de águas entre um tipo de
ruptura e outro. Tal questionamento e o tipo de ruptura por instabilidade geométrica é que
são tratados nos problemas conhecidos tecnicamente por “flambagem”. Nesta seção, serão
tratados somente a flambagem de colunas. Deve-se ter consciência, no entanto, que o
fenômeno da flambagem pode ser crucial em diversas outras instâncias e tipos de
elementos como, por exemplo, em vigas esbeltas.
Coluna Ideal Bi-apoiada
O objetivo desta seção é a obtenção de uma expressão para a carga axial necessária
para romper uma coluna por instabilidade do seu equilíbrio geométrico, isto é, cujo
rompimento está associado à alteração da geometria do elemento estrutural, e não à falha
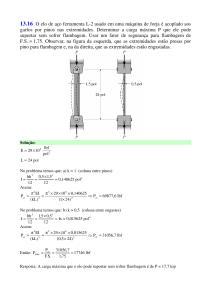
do material de que a coluna é feita. A coluna ilustrada na figura abaixo é considerada
simplesmente apoiada e ideal (feita de um material homogêneo e sem imperfeições de
ordem geométrica).
x
x
v(L) = 0
L
P
EI
v(0) = 0
v(x)
vmáx
A determinação de uma expressão para a flambagem da coluna ilustrada envolve
um equacionamento do seu equilíbrio no estado deformado. A carga P, ao flambar a
coluna, faz com que ela sofra momentos fletores em cada ponto do seu comprimento
afastado x unidades do apoio inferior que valem M(x) = – P v(x). Esta função precisa ser
ENG01140 – Turma C (Prof. Alexandre Pacheco)
46
igual, pela teoria da flexão, a EI v”, onde v” é a derivada segunda de v(x) em relação a x.
Ou seja, a equação diferencial ordinária homogênea, de segunda ordem, e de coeficientes
constantes d2v/dx2 + P/EI v(x) = 0 é a equação que governa a flambagem da coluna biapoiada. Sua solução é a seguinte:
⎛ P ⎞
⎛ P ⎞
v( x) = C1 sin⎜⎜
x ⎟⎟ + C 2 cos⎜⎜
x ⎟⎟
⎝ EI ⎠
⎝ EI ⎠
onde as constantes C1 e C2 podem ser determinadas através das condições de contorno da
coluna:
v(0) = 0 ⇒
⇒
0 = (C1 )(0) + (C 2 )(1)
C2 = 0
⎛ P ⎞
⎛ P ⎞
1 ≠0
v(L ) = 0 ⇒ 0 = C1 sin⎜⎜
L ⎟⎟ + 0 ⎯C⎯
⎯→ sin⎜⎜
L ⎟⎟ = 0
EI
EI
⎝
⎠
⎝
⎠
Na segunda condição, para que o seno seja nulo, a quantidade entre parênteses precisa,
obrigatoriamente, ser sempre múltipla de π radianos, isto é:
P
L = nπ , n = 1, 2, ...
EI
Para n = 1, tem-se o valor da força crítica Pcr necessário para que a coluna saia da sua
posição indeformada para assumir uma geometria arqueada, ou seja, para que sofra
instabilidade do equilíbrio ou flambagem. Este valor é:
Pcr =
π 2 EI
L2
Assim, portanto, a carga crítica para a flambagem de uma coluna ideal bi-apoiada depende,
como comentado inicialmente, do comprimento da coluna, L, e das características
geométricas de sua seção transversal ou, mais precisamente, do seu momento de inércia, I.
Ainda, o material de que a coluna é feita também é importante, pois a força Pcr é
diretamente proporcional ao módulo de elasticidade, E, do material.
Colunas com Outros Tipos de Apoios
Nem sempre as colunas terão as condições de contorno exigidas acima. A
possibilidade de encontrarmos, por exemplo, colunas bi-engastadas ou engastadas-livre é
grande e, portanto, a expressão para cálculo da carga crítica de flambagem precisa ser
adequada a cada caso possível. Na figura a seguir apresentam-se os possíveis casos e suas
deformadas, determinando-se, a partir de suas geometrias deformadas originais, os trechos
em arco como aquele admitido para a coluna bi-apoiada. Assim, se a expressão anterior
para a carga crítica de flambagem era baseada num comprimento equivalente, Le, igual ao
comprimento total da coluna bi-apoiada, L, a partir de agora, para se considerar qualquer
caso possível de vinculação, adota-se, na fórmula, a variável Le, que dependerá das
condições de contorno da coluna. A expressão final é evidenciada abaixo, sendo
conhecida na literatura como “Carga Crítica de Flambagem de Euler”. Esta fórmula,
ENG01140 – Turma C (Prof. Alexandre Pacheco)
47
muitas vezes, aparece ligeiramente modificada para que a tensão, e não a carga, seja
considerada.
P
P
P
P
Le = 0,7 L
Le = L
Le = 0,5 L
Le = 2 L
Pcr =
π2 EI
Le2
Carga Crítica de Euler
Para tanto, deve-se lembrar do conceito de “raio de giração”, r, que nada mais é do que a
raiz quadrada do momento de inércia, I, de uma seção transversal dividida pela área, A,
desta seção, ou seja: r2 = I/A. Aplicando-se esta relação na fórmula da carga crítica de
Euler, obtém-se que:
Pcr =
π 2 EAr 2
L2e
ou
Pcr
π 2E
= 2 2
A Le r
que, finalmente, resulta em:
σ cr =
π 2E
, λe = Le r
λ2e
Nesta última expressão, tem-se que a tensão crítica de flambagem de Euler, σcr, é
diretamente proporcional ao módulo de elasticidade, E, do material e inversamente
proporcional ao quadrado do “índice de esbeltez equivalente ou efetivo”, λe, da coluna.