2ª Série – 2013 MATEMÁTICA MATEMÁTICA – Questões de 01 a 20

2ª Série – 2013
MATEMÁTICA
MATEMÁTICA – Questões de 01 a 20
1)
(SISTEMA EQUIPE) Três moedas são lançadas ao mesmo tempo. Qual é a
probabilidade de as três moedas caírem com a mesma face para cima?
a)
b)
c)
d)
2)
(SISTEMA EQUIPE) Um casal pretende ter filhos. Sabe-se que a cada mês a
probabilidade da mulher engravidar é de 20%. Qual é a probabilidade dela vir
a engravidar somente no quarto mês de tentativas?
a)
b)
c)
d)
3)
10,24%.
0,16%.
40,96%.
0,64%.
(SISTEMA EQUIPE) Em uma caixa há 2 fichas amarelas, 5 fichas azuis e 7
fichas verdes. Se retirarmos uma única ficha, qual a probabilidade dela ser
verde ou amarela?
a)
b)
c)
d)
4)
20%.
22%.
25%.
30%
5/14
1/2
4/7
9/14
(SISTEMA EQUIPE) Alguns amigos estão em uma lanchonete. Sobre a mesa
há duas travessas. Em uma delas há 3 pastéis e 5 coxinhas. Na outra há 2
coxinhas e 4 pastéis. Se ao acaso alguém escolher uma destas travessas e
também ao acaso pegar um dos salgados, qual a probabilidade de se ter
pegado um pastel?
a)
b)
c)
d)
23/48
25/48
29/48
31/48
SISTEMA EQUIPE DE ENSINO
GABARITO 1
1
MATEMÁTICA
5)
(SISTEMA EQUIPE) Em uma caixa há 4 bolas verdes, 4 azuis e 4 vermelhas.
Se tirarmos sem reposição 3 bolas desta caixa, uma a uma, qual a
probabilidade de tirarmos, nesta ordem, bolas nas cores verde, azul e
vermelha?
a)
b)
c)
d)
6)
8/165
3/55
1/4
7/165
(SISTEMA EQUIPE) De uma sacola contendo 15 bolas numeradas de 1 a 15
retira-se uma bola. Qual é a probabilidade desta bola ser divisível por 3 ou
divisível por 4?
a)
b)
c)
d)
7)
2ª Série – 2013
4/15
5/15
6/15
7/15
(SISTEMA EQUIPE) A Mastercard International efetuou um estudo de fraudes
em cartões de crédito; os resultados estão consubstanciados na tabela a
seguir:
TIPO DE FRAUDE
Cartão roubado
Cartão falsificado
Pedido correio/telefone
Outros
NÚMERO
243
85
52
46
Selecionado aleatoriamente um caso de fraude nos casos resumidos na tabela,
qual a probabilidade aproximada de a fraude resultar de um cartão falsificado?
a)
b)
c)
d)
2
18%.
20%.
22%
24%.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2013
8)
(UFPE) O vírus X aparece nas variantes X1 e X2. Se um indivíduo tem esse
vírus, a probabilidade de ser a variante X1 é de 3/5. Se o indivíduo tem o vírus
X1, a probabilidade de esse indivíduo sobreviver é de 2/3; mas, se o indivíduo
tem o vírus X2 , a probabilidade de ele sobreviver é de 5/6. Nessas condições,
qual a probabilidade de o indivíduo portador do vírus X sobreviver?
a)
b)
c)
d)
9)
MATEMÁTICA
1/3
7/15
3/5
11/15
(UFG-GO) Um jogo de memória é formado por seis cartas, conforme as figuras
que seguem:
Após embaralhar as cartas e virar as suas faces para baixo. O jogador deve
buscar as cartas iguais, virando exatamente duas. A probabilidade de ele
retirar, ao acaso, duas carta iguais na primeira tentiva é de :
a)
b)
c)
d)
1/2.
1/3.
1/4.
1/5.
SISTEMA EQUIPE DE ENSINO
GABARITO 1
3
MATEMÁTICA
2ª Série – 2013
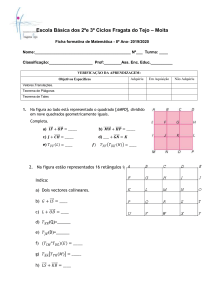
10) (UEL-PR) No diagrama a seguir, o espaço amostral S representa um grupo de
amigos que farão uma viagem. O conjunto A indica a quantidade de pessoas
que já foram a Maceió e o conjunto B, a quantidade de pessoas que já foram a
Fortaleza.
A empresa de turismo que está organizando a viagem fará o sorteio de uma
passagem gratuita. Considerando que a pessoa sorteada já tenha ido para
Fortaleza, assinale a alternativa que indica a probabilidade de que ela também
já tenha ido para Maceió.
a)
b)
c)
d)
18,75%.
30%.
33,33%.
50%.
11) (SISTEMA EQUIPE) Em um poliedro convexo o número de vértices
corresponde a 2/3 do número de arestas, e o número de faces é três unidades
a menos do que o de vértices. Quantas são as faces desse poliedro?
a)
b)
c)
d)
4
7.
8.
9.
10.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2013
MATEMÁTICA
12) (FUVEST) Uma formiga resolveu andar de um vértice a outro do prisma reto
de bases triangulares ABC e DEG seguindo um trajeto especial. Ela partiu do
vértice G, percorreu toda a aresta perpendicular à base ABC, para em seguida
caminhar toda a diagonal da face ADGC e, finalmente, completou seu passeio
percorrendo a aresta reversa a CG.
A formiga chegou ao vértice :
a)
b)
c)
d)
A.
G.
E.
D.
SISTEMA EQUIPE DE ENSINO
GABARITO 1
5
MATEMÁTICA
2ª Série – 2013
13) (FATEC) Na figura a seguir tem-se: o plano 𝜶 definido pelas retas c e d,
perpendiculares entre si; a reta b, perpendicular a 𝜶 em A, com A ∈ c; o ponto
B, intersecção de c e d.
Se X é um ponto de b, X ∉ 𝜶, então a reta s, definida por X e B:
a)
b)
c)
d)
É paralela à reta c.
É paralela à reta b.
Está contida no plano 𝜶
É perpendicular à reta d.
14) (UFMS) Para fazer uma caixa sem tampa com um único pedaço de papelão,
utilizou-se um retângulo de 16 cm de largura e 30 cm de comprimento. De
cada um dos quatro cantos desse retângulo, foram retirados quadrados
idênticos de lados com x cm de comprimento (0<x<8). Depois, foram dobradas
para cima as abas resultantes. A expressão que representa a área lateral da
caixa é:
a)
b)
c)
d)
6
92x - 8x2 cm2.
62x - 6x2 cm2.
72x - 6x2 cm2.
46x - 4x2 cm2.
GABARITO 1
SISTEMA EQUIPE DE ENSINO
2ª Série – 2013
MATEMÁTICA
15) (ACAFE – SC) Num paralelepípedo reto, as arestas da base medem 8 dm e
6 dm, e a altura mede 4 dm. Calcule a área da figura determinada pela
diagonal do paralelepípedo com a diagonal da base e a aresta lateral:
a)
b)
c)
d)
20 dm2.
24 dm2.
32 dm2.
40 dm2.
16) (UDESCO - SC) Aumentando-se em 1 metro a aresta de um cubo, sua área
lateral aumenta em 164 metros quadrado. Então o volume, o volume do cubo
original, em metros, era:
a)
b)
c)
d)
1.000
8.000
27.000
3.375
17) (PUC – SP) Uma caixa d´água, em forma de prisma reto, tem aresta lateral
igual a 6 m e por base um losango cujas diagonais medem 7 m e 10 m. O
volume dessa caixa, em litros é:
a)
b)
c)
d)
42 000
70 000
200 000
210 000
18) (PUC-SP modificada) A altura de um prisma reto mede 8 cm e sua base é um
hexágono regular cujo apótema mede √3 cm. Nessas condições, o volume do
prisma mede:
a)
b)
c)
d)
40√3 cm3.
44√3 cm3.
48√3 cm3.
52√3 cm3.
SISTEMA EQUIPE DE ENSINO
GABARITO 1
7
MATEMÁTICA
2ª Série – 2013
19) (UEPG - PR) Um caleidoscópio tem a forma de um prisma triangular e regular.
Sabendo-se que o apótema de sua base mede √3 cm e sua altura mede 18
cm, a área lateral mede:
a)
b)
c)
d)
162 √3 cm2
972 cm2
108 √3 cm2
324 cm2
20) (FEI) De uma viga de madeira de seção quadrada de lado L = 10 cm extrai-se
uma cunha de altura h=15 cm, conforme a figura. O volume da cunha é:
a)
b)
c)
d)
8
250 cm3.
500 cm3.
750 cm3.
1000 cm3.
GABARITO 1
SISTEMA EQUIPE DE ENSINO