Considere-se o ficheiro de texto “Dados

DEP. INFORMÁTICA - UNIVERSIDADE DA BEIRA INTERIOR
Eng. Informática
Linguagens Formais e Compilação
Resolução da Frequência 1
2º Semestre
20/Abril/2010
Pergunta
A.1
A.2
A.3
A.4
B
C.1
C.2
Total
Cotação
0,75
0,50
0,50
0,75
2,00
0,75
0,75
6,00
A. AUTÓMATOS FINITOS DETERMINÍSTICOS (AFD) E PROGRAMAÇÃO EM C
Considere os seguintes conjuntos: letra = { a, …, z, A, …, Z }, digito = { 0, …, 9 }, hifen = { _ } e
ponto = { . }, e o alfabeto S = letra  digito  hifen  ponto.
1.
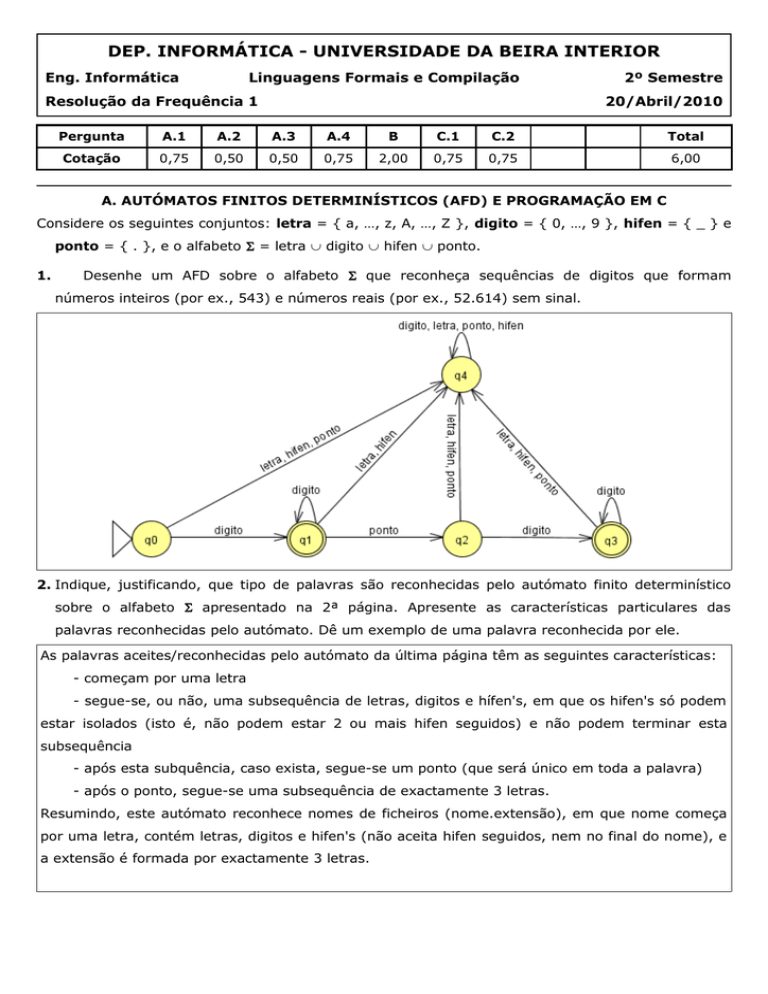
Desenhe um AFD sobre o alfabeto S que reconheça sequências de digitos que formam
números inteiros (por ex., 543) e números reais (por ex., 52.614) sem sinal.
2. Indique, justificando, que tipo de palavras são reconhecidas pelo autómato finito determinístico
sobre o alfabeto S apresentado na 2ª página. Apresente as características particulares das
palavras reconhecidas pelo autómato. Dê um exemplo de uma palavra reconhecida por ele.
As palavras aceites/reconhecidas pelo autómato da última página têm as seguintes características:
- começam por uma letra
- segue-se, ou não, uma subsequência de letras, digitos e hífen's, em que os hifen's só podem
estar isolados (isto é, não podem estar 2 ou mais hifen seguidos) e não podem terminar esta
subsequência
- após esta subquência, caso exista, segue-se um ponto (que será único em toda a palavra)
- após o ponto, segue-se uma subsequência de exactamente 3 letras.
Resumindo, este autómato reconhece nomes de ficheiros (nome.extensão), em que nome começa
por uma letra, contém letras, digitos e hifen's (não aceita hifen seguidos, nem no final do nome), e
a extensão é formada por exactamente 3 letras.
3. Construa a tabela das d-transições do autómato finito determinístico apresentado na 2ª página.
símbolos terminais
estados
letra
digito
hifen
ponto
q0
q1
q9
q9
q9
q1
q1
q1
q2
q4
q2
q3
q3
q9
q9
q3
q1
q1
q2
q4
q4
q5
q8
q8
q8
q5
q6
q8
q8
q8
q6
q7
q9
q9
q9
q7
q9
q9
q9
q9
q8
q8
q8
q8
q8
q9
q9
q9
q9
q9
4. Implemente em linguagem C o autómato finito determinístico apresentado na 2ª página.
int delta (int q, char ch)
{
int M[10][4] = { 1, 9, 9, 9, 1, 1, 2, 4, 3, 3, 9, 9, 1, 1, 2, 4, 5, 8, 8, 8, 6, 8, 8, 8, 7, 9, 9, 9, 9
9, 9, 9, 8, 8, 8, 8, 9, 9, 9, 9 }
if (ch >= 'a' && ch <= 'z' || ch >= 'A' && ch <= 'Z' )
return (M[q][0]);
else if (ch >= '0' && ch <= '9')
return (M[q][1]);
else if (ch == '_')
return (M[q][2]);
else
return (M[q][3]);
}
int main ()
{
int q_actual, k;
char st[100];
puts (“Introduza uma sequência de letras, digitos, hifen e pontos : “);
gets(st);
for (k = 0; k < strlen(st); k++)
q_actual = delta (q_actual, st[k]);
if (q_actual == 7)
printf (“%s é aceite pelo autómato.\n”, st);
else
printf (“%s não é aceite pelo autómato.\n”, st);
}
B. LEX
Implemente um programa em LEX que, dado um texto :
–
substitua a palavra UBI pela palavra DIUBI em todas as suas ocorrências;
–
determine o número de ocorrências da palavra UBI;
–
determine o número de palavras começadas pelos caracteres a ou A;
–
determine o número de palavras com 5 ou mais letras;
–
determine o número de palavras com 2 ou mais b's;
–
determine o número de reais (em formato de ponto flutuante: 0.65) entre 0 e 2.
(NOTA: palavra = sequência de letras.)
%{
int cont1 = 0, cont2 = 0, cont3 = 0, cont4 = 0, cont5 = 0;
%}
%%
UBI
{ cont1++; printf (“DIUBI”); }
[aA][a-zA-Z]*
{ cont2++; }
[a-zA-Z]{5}[a-zA-Z]*
{ cont3++; }
[ac-zAC-Z]*b[ac-zAC-Z]*b[a-zA-Z]*
{ cont4++; }
[01]”.”[0-9]+ | 2”.”0+
{ cont5++; }
%%
int main()
{
yylex();
printf (“Número de ocorrências da palavra UBI = %d\n”, cont1);
printf (“Número de palavras começadas pelos caracteres a ou A = %d\n”, cont2);
printf (“Número de palavras com 5 ou mais letras = %d\n”, cont3);
printf (“Número de palavras com 2 ou mais b's = %d\n”, cont4);
printf (“Número de reais (em formato de ponto flutuante: 0.65) entre 0 e 2 = %d\n”, cont5);
return 0;
}
C. FIRST e FOLLOW
Considere a seguinte gramática G = (Σ, T, P, S), em que Σ = { S, A, B, C, D }, T = { a, b, c, d, e, f }
e P = { S → DC; A → e | a | Cb; B → e | c | dA; C → e | f; D → AB }
1. Determine o conjunto First dos símbolos terminais e não terminais de G.
First (a) = { a }
First (b) = { b }
First (c) = { c }
First (d) = { d }
First (e) = { e }
First (f) = { f }
First (S) = { a, e, f, c, d }
First (A) = { ε, a, e, f }
First (B) = { ε, c, d }
First (C) = { e, f }
First (D) = { ε, a, e, f, c, d }
Utilizando A → ε, tira-se o seguinte :
ε ∈ First (A)
Utilizando A → a, tira-se o seguinte :
a ∈ First (A)
Utilizando B → ε, tira-se o seguinte :
ε ∈ First (B)
Utilizando B → c, tira-se o seguinte :
c ∈ First (B)
Utilizando C → e, tira-se o seguinte :
e ∈ First (C)
Utilizando C → f, tira-se o seguinte :
f ∈ First (C)
Utilizando B → d A, tira-se o seguinte :
First (d A )  First (B)
First (d A ) = First (d )  First (A ) (se d deriva e)
Como d não deriva e, apenas d ∈ First (B)
Utilizando A → C b , tira-se o seguinte :
First (C b ) ⊂ First (A)
First (C b ) = First (C) - { e }  First (b ) (se C deriva e)
Como C não deriva e, (pois ε ∉ First (C) e First (C) é final), apenas First (C) ⊂ First (A).
Logo, { e, f } ⊂ First (A)
Utilizando D → A B , tira-se o seguinte :
First (A B ) ⊂ First (D)
First (A B ) = First (A) - { e }  First (B) - { e } (se A deriva e)  { e } (se A, B derivam e)
Como A, B derivam e, (ε ∈ First(A) e ε ∈ First(B)), First (A B ) = First (A)  First (B)  { e }
Logo, { a, e, f }  { c, d }  { e } = { a, e, f, c, d, e } ⊂ First (D)
Utilizando S → D C , tira-se o seguinte :
First (D C ) ⊂ First (S)
First (D C ) = First (D) - { e }  First (C) - { e } (se D deriva e)  { e } (se D, C derivam e )
Como D deriva e (ε ∈ First(D)) e C não deriva e (ε  First(D)), First(D C ) = First(D)  First(C)
Logo, { a, e, f, c, d }  { e, f } = { a, e, f, c, d } ⊂ First (S)
2. Determine o conjunto Follow dos símbolos não terminais de G.
Follow (S) = { $ }
Follow (A) = { c, d, e, f }
Follow (B) = { e, f }
Follow (C) = { $, b }
Follow (D) = { e, f }
Utilizando S → D C , tira-se o seguinte :
First (C) - { e } ⊂ Follow (D). Logo, { e, f } ⊂ Follow (D)
Follow (S) ⊂ Follow (D), se C deriva e. Como C não deriva e (ε  First(C)), não se faz nada.
Follow (S) ⊂ Follow (C). Logo, $  Follow(C)
Utilizando D → A B , tira-se o seguinte :
First (B) - { e } ⊂ Follow (A). Logo, { c, d } ⊂ Follow (A)
Follow (D) ⊂ Follow (A), se B deriva e.
Como B deriva e (ε  First(B)), Follow (D) ⊂ Follow (A). Logo, { e, f } ⊂ Follow (A)
Follow (D) ⊂ Follow (B). Logo, { e, f } ⊂ Follow (B)
Utilizando A → ε :
Não se tira qualquer resultado.
Utilizando A → a :
Não se tira qualquer resultado.
Utilizando A → C b , tira-se o seguinte :
First (b)  Follow (C). Logo, b ∈ Follow (C)
Utilizando B → ε :
Não se tira qualquer resultado.
Utilizando B → c :
Não se tira qualquer resultado.
Utilizando B → d A , tira-se o seguinte :
Follow (B) ⊂ Follow (A). Logo, { e, f } ⊂ Follow (A)
Utilizando C → e :
Não se tira qualquer resultado.
Utilizando C → f :
Não se tira qualquer resultado.
ATENÇÃO: Rever todas as relações entre FOLLOW's.
Expressão regular Significado
Expressão regular Significado
x
Caracter “x”
“x” ou \x
Caracter “x”
[xy] ou x|y
Caracter x ou y
[x-y]
Caracteres entre x e y
[^x]
Todos os caracteres excepto x
.
Qualquer caracter excepto “\n”
x?
Caracter x opcional
()
Associação de expr. regulares
x*
x repetido 0 ou mais vezes
x+
x repetido 1 ou mais vezes
x{n}
Repetição de x n vezes
x{n,m}
Repetição de x n a m vezes
^x
O caracter “x” deve aparecer no início da linha
x$
O caracter “x” deve aparecer no fim da linha