exemplos resolvidos da aula 01-tópico 03

AULA 1. CARGA ELÉTRICA – LEI DE COULOMB
TÓPICO 3 – FORÇA ELÉTRICA: A LEI DE COULOMB
EXEMPLOS RESOLVIDOS DA AULA 01-TÓPICO 03.
Tente responder antes de ver a solução.
Exemplo 1:
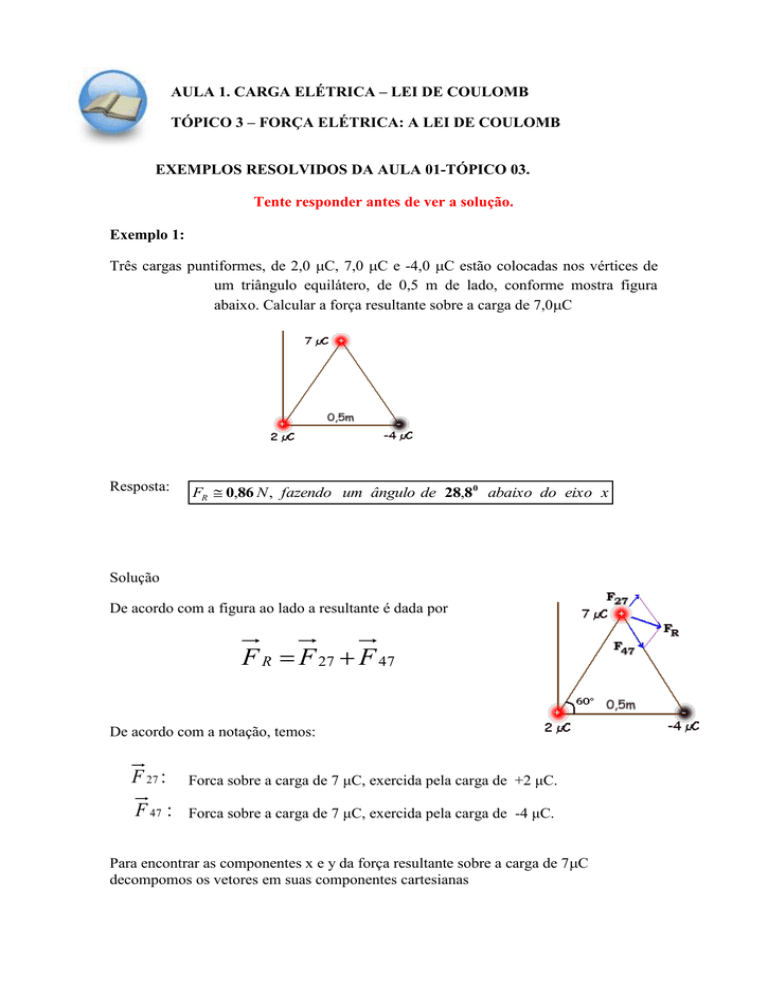
Três cargas puntiformes, de 2,0 C, 7,0 C e -4,0 C estão colocadas nos vértices de
um triângulo equilátero, de 0,5 m de lado, conforme mostra figura
abaixo. Calcular a força resultante sobre a carga de 7,0C
Resposta:
FR  0,86 N , fazendo um ângulo de 28,80 abaixo do eixo x
Solução
De acordo com a figura ao lado a resultante é dada por
F R  F 27  F 47
De acordo com a notação, temos:
F 27 :
Forca sobre a carga de 7 μC, exercida pela carga de +2 μC.
F 47 :
Forca sobre a carga de 7 μC, exercida pela carga de -4 μC.
Para encontrar as componentes x e y da força resultante sobre a carga de 7C
decompomos os vetores em suas componentes cartesianas
FRx  F27 cos 60 0  F47 cos 60 0
FRy  F27 sen 60 0  F47 sen 60 0
Usando a Lei de Coulomb, podemos calcular os módulos das forças F27 e F47
F27
q 2 q7
2  10 6  7  10 6
9
k
 9  10 
 0,5 N
0,25
(0,5) 2
q 4 q7
4 10 6  7 10 6
9
F47  k
 9 10 
 2F72 1,0 N
0,25
(0,5) 2
Usando os valores para o seno e cosseno do ângulo dado:
sen600 
3
 0,866,
2
cos 600  0,5
Teremos apenas que substituir os valores e encontrar as componentes da força
resultante:
Componente x:
FRx = 0,75 N ( apontando para a direita)
Componente y:
FRy = 0,43 N ( apontando para baixo)
Usando o teorema de Pitágoras:
FR  ( FRx ) 2  ( FRy )2  0,86 N
Para calcular a direção da resultante, calculamos a tangente do ângulo que ela faz com a
horizontal:
tg 
FRy
FRx
Substituindo os valores encontramos um ângulo 
  28,80 abaixo do eixo horizontal
Exemplo 2
Duas pequenas esferas idênticas, carregadas, cada qual com
massa de 3 x 10- 2kg estão penduradas e em equilíbrio,
Conforme mostra a figura abaixo. Se o comprimento do fio for
0,15 m e o ângulo =5°, calcular o módulo da carga sobre cada
esfera, supondo que as esferas tenham cargas idênticas.
http://www.if.ufrgs.br/fis/EMVirtual/cap1/cargas.htm
Resposta: q=0,044 C
Solução:
As duas cargas estão em equilibrio pela ação de três forças, a saber, a força elétrica de
repulsão entre as cargas, a força gravitacional e a tensão na corda. Fazendo o diagrama
de forças sobre a carga da esquerda, por exemplo, temos a situação ilustrada abaixo.
Assim, em componentes cartesianas,
Substituindo os valores dados, temos
Como
Exemplo 3
Duas partículas 1 e 2, com cargas iguais e de sinais opostos, afastadas
de 5 m são largadas a partir do repouso. As partículas têm massas
iguais a m1=0,05 kg e m2=0,25 kg, e a aceleração inicial da primeira
partícula é de 100 m/s2. Quais são:
a) a aceleração da segunda partícula?
b) O módulo da carga comum?
Respostas: a) 20 m/s2; b) 178 C
Solução:
Considere a figura abaixo:
2
1

F 12
F 21
d
Dados do problema:
m1=0,05 kg
m2=0,025 kg

a1= 100 m/s2
d=5 m
a2 = ?
q1 =q2 =?
Como sabemos da Segunda Lei de Newton o módulo da força é dado por:
F  ma
Então calculando o módulo da força sobre a carga q1 teremos:
F21  m1a1  0,05  100  F21  5N
A carga 2 exerce a força de 5N sobre a carga 1 (F21.=5 N). Como sabemos as forças
entre as cargas obedecem à Terceira Lei de Newton (Ação e Reação)
Então temos que a força que a carga e exerce sobre a carga 2 é: F12= 5 N
Aplicando novamente a Segunda Lei de Newton: F
F12  m2a 2  0,25  a 2  a 2 
F12
5

m2 0,25
a 2  20 m / s 2
Veja como a resposta está coerente com a Segunda Lei de Newton: a carga 2
por ter maior massa terá menor aceleração
Para calcular o valor da carga, vamos aplicar a Lei de Coulomb:
F k
q1q2
d2
Como as cargas têm o mesmo valor (q1=q e q2= - q), o módulo da força entre elas será:
F  5  9 109 
q2
q2
5
9

9

10

 0,36 109  q 2  q 2 
 13,9 109
2
9
5
25
0,36 10
q  17,8 105 C ou q  178 C
Exemplo 4
Duas cargas puntiformes, q1=+q e q2=+4q, estão separadas por uma distância L, como
mostra a figura abaixo Uma terceira carga deve ser colocada de forma
que o sistema inteiro fique em equilíbrio. Determinar o sinal, o módulo
e a localização da terceira carga.
Resposta: - 4q/9
Solução:
( Fonte: http://www.if.ufrgs.br/fis/EMVirtual/cap1/cargas.htm) Como as duas cargas são de
mesmo sinal, a força entre elas é repulsiva, de modo que apenas uma carga negativa
colocada entre elas pode equilibrar o sistema, conforme mostra a figura ao lado. Assim,
para o equilíbrio, devemos ter
Para você se exercitar, desenhe as forças que agem sobre as cargas
A condição de equilíbrio imposta ao sistema exige que:
(1)
(2)
(3)
Observe que F21: representa a força sobre a carga 2, exercida pela carga 1, e assim por
diante. Isso reforça aquela observação anterior de que esta notação é arbitrária. Ao
resolver um exercício, você pode escolher qual notação usar, desde que permaneça fiel à
notação usada em toda a resolução do exercício
Da terceira das equações, temos
onde
escolhemos o sinal +, tendo em vista que x deve estar entre as cargas. Para calcular o
módulo da terceira carga, usamos, p. ex., a eq.(1), ou seja,
assim encontramos o módulo da carga q3: